Многофункциональная метаповерхность графена для генерации и управления вихревыми волнами

Введение

Графен, инновационный 2D-материал с атомной толщиной, привлекает все больше и больше внимания в биологии, оптоэлектронике, терагерцовой связи и т.д. [1]. В терагерцовом режиме графен имеет лучшие характеристики по сравнению с обычным благородным металлом из-за поддержки распространения поверхностных плазмонных поляритонов (SPP) [2], что делает его очень многообещающим кандидатом в терагерцовой технологии. Поэтому в последние годы появилось большое количество устройств на основе графена в терагерцовом и среднем инфракрасном диапазонах, таких как модуляторы [3–6], детекторы [7], поглотители [8, 9] и лазеры [10, 10]. 11].

Очень важно проектировать и производить реконфигурируемые метаматериалы для управления поведением электромагнитных волн [12, 13]. Поэтому многие механизмы настройки были реализованы в различных различных частотных диапазонах [14], таких как электрически реконфигурируемые метаматериалы [15], механически реконфигурируемые метаматериалы [16], нелинейные материалы [17], жидкие кристаллы [18], микрожидкости [ 19], полупроводниковые структуры [20] и графен [21]. Графен, как инновационный материал, является выдающимся кандидатом среди них, в основном из-за его электрической / магнитной контролируемой проводимости, которая позволяет разрабатывать и изготавливать миниатюрные управляемые устройства [14, 22]. Следовательно, он имеет большой потенциал для разработки реконфигурируемой метаповерхности, и многие приложения, основанные на его настраиваемости, были предложены в [23] и [24]. Применяя обобщенный закон Снеллиуса [25, 26], аномальное отражение может быть настроено и реализовано метаповерхностями графена [27]. Эти работы могут открыть путь к разработке и производству перестраиваемых терагерцовых устройств.

В телекоммуникациях орбитальный угловой момент (OAM) важен для увеличения пропускной способности канала, поскольку он может обеспечить бесконечное состояние [28, 29]. Трехмерный метаматериал можно использовать для генерации волны OAM [30]. Метаповерхность, которую можно рассматривать как двухмерный метаматериал, может обеспечить выдающиеся характеристики при толщине субволновой волны. В микроволновом режиме метаповерхности широко используются для проектирования и изготовления устройств субволновых размеров для генерации волн с различной поляризацией и свойствами усиления [31–34]. Сообщалось, что в терагерцовом режиме отражающая метаповерхность графена генерирует вихревые волны с возможностью настройки [35]. Метаповерхность графена обладает гибкостью для управления волновым фронтом [36]; Следовательно, можно ожидать, что осуществимая конструкция, сочетающая в себе функции генерации вихревых волн и аномального отражения, позволит настроить направленность вихревых волн с высокой точностью.

В этой работе, основанной на наших предыдущих исследованиях метаповерхностей в микро-нанооптике [37–41], мы изучаем механизм объединения функций двух метаповерхностей. Графеновая ячейка анализируется, чтобы получить взаимосвязь между коэффициентом отражения и ее химическим потенциалом, а также размером пятна. Полный 360 ^∘ Диапазон фазы отражения откалиброван как эталон для проектирования метаповерхности графена, объединяющей функции генерации вихревых волн и аномального отражения. Комбинированная метаповерхность реализована большим массивом отражающих графеновых ячеек. Результаты моделирования показывают, что вихревые волны могут генерироваться и управляться под определенным углом отражения.

Методы

Проводимость графена состоит из межзонного и внутризонного перехода. Внутризонный переход доминирует в терагерцовом и инфракрасном режимах, а межзонный переход доминирует в видимом оптическом режиме. В терагерцовом и инфракрасном диапазонах проводимость можно смоделировать с помощью модели Друде [24],

где k _B постоянная Больцмана, T - температура, τ - время релаксации, а E _f энергия Ферми.

В данной работе устройство работает в терагерцовом режиме, где E _f ≫ к _B Т ; следовательно, уравнение можно упростить как

принимая типичное значение комнатной температуры T =300 тыс. , а время релаксации графена τ =1 шт. В этой работе энергия Ферми E _f контролируется внешним статическим напряжением затвора. При моделировании графен моделируется не как трехмерные блоки метаматериала, а как двумерные поверхностные проводящие условия из-за атомной толщины.

Метаповерхность графена состоит из большого массива графеновых ячеек, что приводит к коллективному плазмонному поведению, возбужденному на поверхности, проявляющему необычные электромагнитные свойства. Частота 1,3 ТГц; таким образом, из-за распространения медленной волны, связанной с плазмонной модой, резонанс может возникать при очень малых размерах, т.е. е., ниже λ / 10 [23, 42]. Чтобы спроектировать метаповерхность графеновых ячеек, извлекается калибровочный график отражательного поведения графеновой ячейки, чтобы детально изучить влияние каждого параметра в одной графеновой ячейке.

Типичная элементарная графеновая ячейка, как показано на рис. 1, состоит из многослойной структуры с графеновым пятном атомной толщины, установленным наверху. Графеновый патч размером w _x × ш _y устанавливается по центру поверх стопки многослойных квадратных подложек со сторонами p 14 мкм. Кварцевая подложка ( ε _r =3,75, тангенс δ =0,0184) толщиной 25 мкм помещается поверх металлического грунтового слоя внизу. Между графеновым пятном и слоем поликристаллического кремния толщиной 50 нм прикладывается внешнее смещающее постоянное напряжение. Al ₂ толщиной 10 нм О ₃ (Глинозем, \ (\ epsilon _ {r} =8.9, \ tan \ delta =0,01 \)) слой вставляется между ними в качестве разделителя. Химический потенциал можно регулировать от 0,01 до 1,0 эВ, управляя внешним смещающим постоянным напряжением от 0 до 14,7 В [23, 35]. Следует отметить, что слой поликристаллического кремния и прокладка из оксида алюминия не моделируются при моделировании в этой статье по следующим причинам. Во-первых, выполняется отдельное 2D-моделирование, которое намного дешевле, чтобы показать, что, поскольку толщина слоя поликристаллического кремния и прокладки из оксида алюминия намного меньше, чем у кварцевой подложки, их влиянием на отражательную способность можно пренебречь. С другой стороны, при моделировании методом конечных элементов требуется огромное количество элементов при работе с соседними объектами с огромной разницей в размерах. В результате трехмерное моделирование этих двух слоев будет чрезвычайно дорогостоящим.

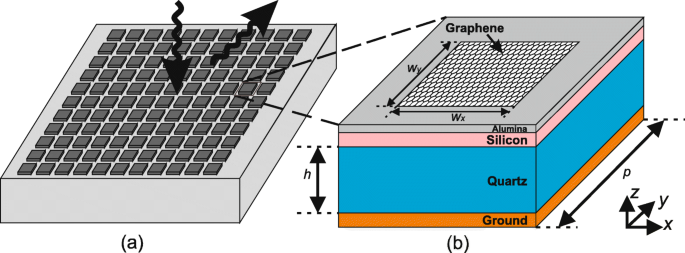
Иллюстрация метаповерхности графена и конфигурации ячейки. а Схема метаповерхности графена, которая может управлять входящими электромагнитными волнами путем аномального отражения. б Конфигурация графеновой ячейки, состоящей из многослойной подложки и установленного графенового пятна размером w _x × ш _y . Между графеновым участком и слоем кремния прикладывается статическое напряжение затвора для управления химическим потенциалом

Чтобы изучить отражающие свойства, на которые влияет μ _c и w _x , периодические условия назначаются в обоих x и y направления. Волна падает сверху нормально с параллельной поляризацией, то есть с электрическим полем, поляризованным в x -направление. Поскольку графен эквивалентен сложному условию поверхностной проводимости, только w _x может повлиять на проводимость в x -направление значительно, а w _y оказывает незначительное влияние и во всех моделированиях в этой статье фиксируется как 4 мкм.

Чтобы тщательно изучить влияние размера пятна и химического потенциала, мы анализируем w _x от 0,2 до 13,8 мкм с шагом 0,2 мкм и развертка мкм _c от 0,01 до 1,00 эВ с шагом 0,01 эВ, а частота зафиксирована на уровне 1,3 ТГц. Фаза и величина S ₁₁ представлены на рис. 2, которые называются калибровочными графиками, поскольку значение w _x и μ _c можно откалибровать по ним. Чтобы гарантировать эффективность метаповерхности, величина коэффициента отражения должна быть больше 0,7; таким образом, неквалифицированные регионы выкапываются как пустые. На калибровочном графике получается полный охват 360 ^∘ чего достаточно для построения метаповерхностей графена.

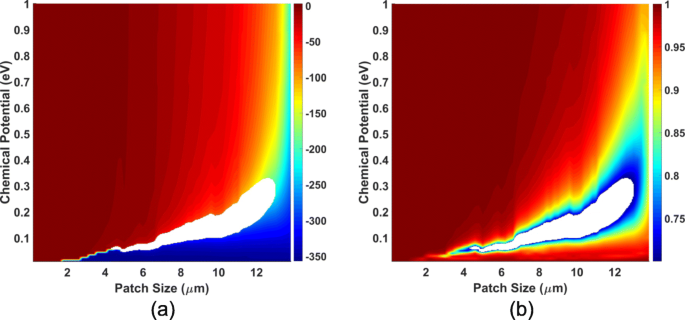
Градуировочная диаграмма коэффициентов отражения графеновой ячейки. Коэффициент отражения графеновой ячейки под влиянием размера графенового пятна w _x и химический потенциал μ _c , где вычитается область, в которой величина отражения меньше 0,7. а фаза и b диаграмма величин

Фазовая диаграмма должна быть достаточно гладкой, чтобы точно контролировать фазу. Чтобы спроектировать параметры графеновых ячеек для достижения полного фазового покрытия от 0 ^∘ на 360 ^∘ , семь комбинаций w _x и μ _c выбраны, как показано на рис. 3.

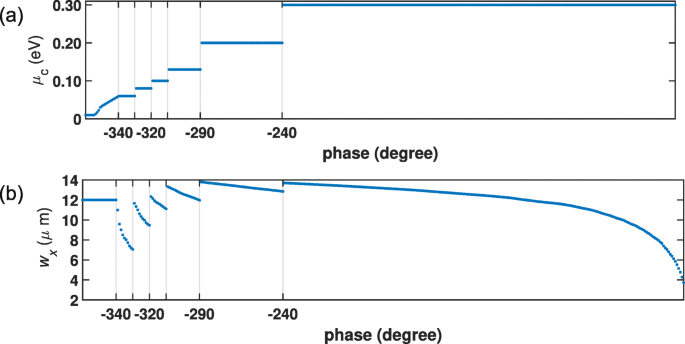
Схема конструкции графеновой ячейки. Полный 360 ^∘ охват фазы достигается семью группами комбинаций a химический потенциал и b размер патча

Результаты и обсуждения

Для реализации различных функций было бы очень полезно объединить функциональные возможности двух метаповерхностей или добавить новые функции в другую. Эта методология предоставит универсальный способ проектирования новых метаповерхностей. В этой статье мы объединяем функции генерации вихревых волн и отклонения волн за счет аномального отражения.

Ниже предлагается обобщенная методология объединения двух метаповерхностей MS ₁ и MS ₂ в одну многофункциональную метаповерхность MS _t . Чтобы реализовать комбинацию, начнем с обобщенного закона отражения [25]. Как показано на рис. 4, рассмотрим плоскую волну с длиной волны в свободном пространстве λ падает с углом падения θ _я , следующее уравнение описывает обобщенный закон отражения,

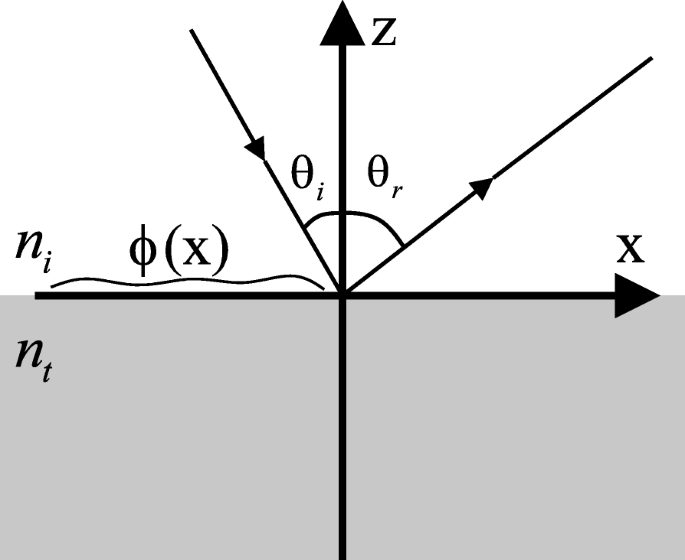
Иллюстрация обобщенного закона отражения. Электромагнитная волна падает сверху с падающим ангелом θ _я , а отражается θ _r кроме θ _я , из-за скачка фазы ϕ ( x ) вдоль интерфейса

где θ _r угол отражения, n _я - показатель преломления в верхнем пространстве, а ϕ ( x ) описывает скачок фазы вдоль границы раздела.

Рассмотрим упрощенный случай, когда волна падает нормально, а верхнее пространство является свободным пространством ( n _я =1), как показано на рис.5, для первых двух метаповерхностей MS ₁ и MS ₂ , Уравнение 1 можно упростить как

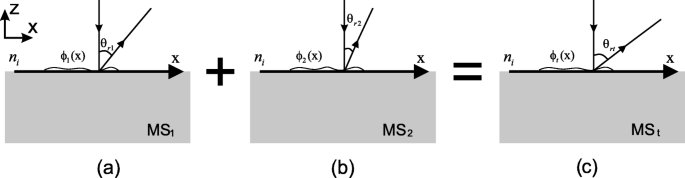
Иллюстрация объединения двух метаповерхностей в одну многофункциональную метаповерхность. На вставке электромагнитные волны падают нормально из верхнего пространства с показателем преломления n . _я . а Metasruface 1 (MS ₁ ) с разрывом фазы ϕ ₁ ( x ) и b метаповерхность 2 (MS ₂ ) с разрывом фазы ϕ ₂ ( x ) объединяются в c желаемая многофункциональная метаповерхность (MS _t ) с разрывом фазы ϕ _т ( x ). θ _{r 1} ( x ), θ _{r 2} ( x ) и θ _rt ( x ) - углы аномального отражения вдоль границ раздела метаповерхностей, соответственно, и соотношение θ _rt ( x ) = θ _{r 1} ( x ) + θ _{r 2} ( x ) выполняется всюду в MS _t

Чтобы получить ϕ _т MS _t , выбираем отрезок D _x вдоль интерфейса, и проблема становится следующей:предположим, что в x ∈ D _x , имеет место - π / 2 < θ _{r 1} ( x ) + θ _{r 2} ( x ) < π / 2, найти ϕ _т , с. т. для ∀ x ∈ D _x , что

Это может быть получено из формул. 2 и 3, что

что приводит к

где член интегрирования вычисляет вклад дисперсии θ _ри ( x ) и в большинстве случаев может быть рассчитан численно. Уравнение 5 играет жизненно важную роль для объединения функций двух метаповерхностей.

Кроме того, если угол поворота постоянный, член интегрирования в формуле. 6 исчезает. Уравнение 5 можно значительно упростить как

Это основное уравнение для объединения метаповерхностей, а распределение фаз можно рассчитать для объединения генерации вихревой волны и аномального отражения.

В этой статье MS ₁ - метаповерхность, которая генерирует вихревые волны, а MS ₂ это метаповерхность, которая управляет волнами.

Как показано в [35], вихревые волны с модой l может быть сгенерирована пластиной из N секторов с последовательным приращением фазового сдвига. Фазовый сдвиг n ый сектор ϕ _n можно рассчитать как ϕ _n = ϕ ₀ +2 π нет l / N , где ϕ ₀ - фазовый сдвиг начального сектора. Более того, чтобы сгенерировать вихревую волну, должно быть выполнено - N / 2 < l < N / 2. Следовательно, N =4 достаточно для генерации режимов l =0, ± 1.

Чтобы сгенерировать вихревую волну с помощью l =1 пластина разделена на четыре сектора, как показано на рис. 6а. Состояние фазы ϕ ₁ ( x , y ) - кусочно-постоянная функция, убывающая на 90 ^∘ через секторы против часовой стрелки.

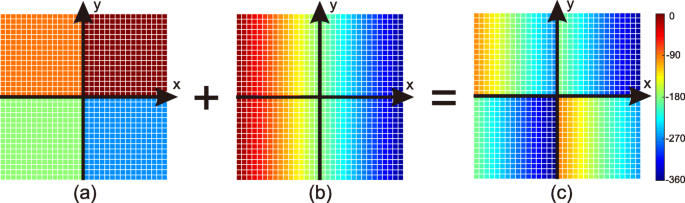
Иллюстрация комбинации функций разрыва фазы. а ϕ ₁ , распределение скачков фазы МС ₁ , который генерирует вихревую электромагнитную волну с l =1. б ϕ ₂ , распределение скачков фазы МС ₂ , что приводит к аномальному отражению. c Комбинированное распределение скачков фаз МС _t рассчитывается по формуле. 6

Когда x -поляризованная волна падает нормально сверху, вихревая волна с l =1 будет отражено. Следует отметить, что волна отражается вертикально; следовательно, угол отклонения равен 0 ^∘ , т.е. θ _{r 1} ( x ) =0 ^∘ .

Для создания аномального отражения с углом отклонения θ _r , Уравнение 1 применяется. Как показано на рис. 4, когда волна падает нормально в свободном пространстве, т. Е. θ _я =0 ^∘ и н _я =1, уравнение. 1 сокращается до

В данной работе угол отклонения установлен как θ _r =30 ^∘ . Из приведенного выше уравнения, зная, что период элементарной ячейки составляет 14 мкм, разница фазового сдвига между соседними участками вычисляется как 10,9 ^∘ . Распределение фаз показано на рис. 6б.

Чтобы объединить MS ₁ и MS ₂ берем θ _{r 1} ( x ) =0 ^∘ и θ _{r 2} ( x ) =30 ^∘ в уравнение. 6 и получите расчетную формулу MS _t ,

По этой формуле можно рассчитать фазовое распределение, показанное на рис. 6в. Согласно рис. 3, выбирая химические потенциалы μ _c и размер патча w _x каждой ячейки конфигурируется метаповерхность графена размером 32 × 32. На рис. 1а показан вид сверху размещения графеновых ячеек на метаповерхности. Видно, что каждый сектор представляет собой подобласть размером 16 × 16, состоящую из 16 столбцов по вертикали. И каждый столбец состоит из 16 одинаковых графеновых пятен, где определенная комбинация w _x и μ _c назначается.

Пластина возбуждается x -поляризованная волна, падающая сверху. Электрическое поле падающей волны нормировано, т.е. \ (\ vec {\ mathrm {E}} _ {\ text {inc}} =\ vec {x} \). Моделирование проводилось с использованием коммерческого решателя конечных элементов COMSOL Multiphysics 5.2. Графен имеет атомную толщину; однако толщина подложек измеряется в микрометрах. Следовательно, вычислительные усилия будут огромными, если трехмерное построение сетки будет применено к графеновым пятнам. Поэтому толщина графеновых пятен не учитывается, и эквивалентное условие двумерной поверхностной проводимости применяется в качестве граничных условий перехода в COMSOL Multiphysics. На пластине размещены участки размером 32 × 32, которые разделены на четыре сектора. На каждом секторе есть участки размером 16 × 16, которые контролируются независимо по их размерам и химическим потенциалам. Для моделирования использовалось 7,1 миллиона степеней свободы, которое проводилось на сервере с потоками 40 × 2,1 ГГц и 256 ГБ памяти.

На рис. 7б показана величина электрического поля отраженной волны, нормированная падающей волной. Метаповерхность графена генерирует вихревую волну с l =1 и отклоняется на 30 ^∘ в сторону x ось.

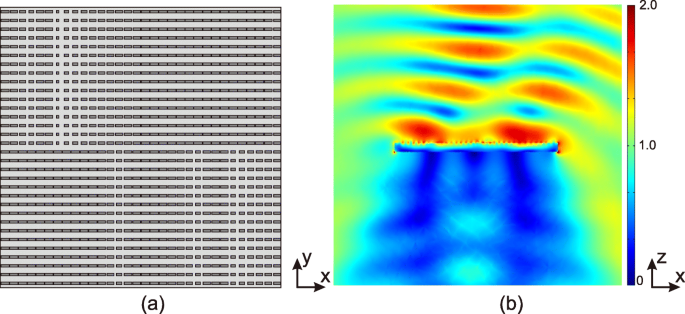
Результаты многофункциональной метаповерхности. а Конфигурация пластины с графеновым отражателем, состоящим из 36 × 36 графеновых пятен. Ширина ( w _y ) всего графенового пятна принимается равным 4 мкм, а значения w _x выбраны для реализации условия прерывания фазы, как показано на фиг. 6. b Величина электрического поля отраженной вихревой волны l =1. Падающая волна - это x -поляризованная электромагнитная волна с нормированным электрическим полем, нормальная падающая сверху. Волна отклоняется на 30 ^∘ в сторону x -направление

Выводы

Таким образом, мы изучили принцип построения многофункциональных метаповерхностей графена. Предлагается методика объединения двух метаповерхностей. Например, метаповерхность графена предназначена для объединения функций генерации вихревой волны и управления волнами. Графен представляет собой двумерный атомарный материал толщиной, который может динамически настраивать фазовое состояние, прикладывая внешние напряжения затвора. Его параметры тщательно исследуются для калибровки отражательного поведения отдельной графеновой ячейки и получения покрытия в 360 ^∘ сдвиг фазы. Метаповерхность графена, состоящая из 32 × 32 элементарных ячеек, предназначена для реализации аномального отражения и одновременной генерации вихревой волны ТГц диапазона. Результаты моделирования показывают, что вихревая волна с l =1 создается и управляется. Графен демонстрирует много необычных свойств в терагерцовом режиме, таких как поддержка SPP, высокая эффективность и настраиваемость; следовательно, это многообещающий кандидат в терагерцовом диапазоне. В этом исследовании исследуется подход к объединению функций различных метаповерхностей, реализованный с помощью графена, который открывает ворота динамически управляемых многофункциональных метаповерхностей в терагерцовом режиме.

Доступность данных и материалов

Наборы данных, созданные во время и / или проанализированные в ходе текущего исследования, доступны у соответствующих авторов по разумному запросу.

Сокращения

OAM:

Орбитальный угловой момент

SPP:

Поверхностный плазмон-поляритон