Двойное управление нелинейностью моды и дисперсионных свойств в плазмонном волноводе с графеном и диэлектриком

Фон

Плазмоника графена привлекла широкое внимание [1,2,3,4] из-за уникальных электронных и оптических свойств графена по сравнению с металлами. В ТГц и дальнем инфракрасном диапазоне частот преобладает внутризонный переход электронов, и графен ведет себя как металл. Следовательно, поверхностные плазмон-поляритоны (ПП) могут поддерживаться графеном. Для многослойной композитной структуры графен-диэлектрик исследованы процессы возбуждения, связи и распространения ППП. Квазипоперечная электромагнитная мода была обнаружена в волноводе с параллельными пластинами из графена [5]. Связь ППП исследовалась [6, 7] в многослойной структуре графен-диэлектрик. Для структуры периодической матрицы из однослойного листа графена сильная связь между SPP возникает, когда листы графена расположены плотно.

Значительные усилия были посвящены исследованию оптических свойств нелинейных композитных структур графен-диэлектрик [8,9,10,11,12] из-за их большого потенциала в управлении распространением света на микро- и наномасштабах. Для случая однослойного графена обсуждались поверхностные плазмоны на границе раздела графена и нелинейной подложки типа Керра [8]. Показано, что длину волны графеновых плазмонов можно настраивать, регулируя нелинейную диэлектрическую проницаемость подложек. Для многослойной структуры графен-нелинейный диэлектрик были исследованы свойства распространения и локализации графеновых плазмонов и получены точные дисперсионные соотношения для поверхностных TM-плазмонов графенового волновода с параллельными пластинами [11]. На длину распространения и локализацию заметно влияет настройка нелинейной диэлектрической проницаемости. Недавно было получено дисперсионное соотношение для симметричных и антисимметричных плазмонных мод в структуре керрового слоя, покрытой графеном [12]. За исключением типичного режима прямого распространения, были обнаружены симметричный и антисимметричный режимы.

На основе сильной нелинейности графена было предсказано несколько нелинейных оптических эффектов [13,14,15,16,17]. Нестеров и др. [15] исследовали нелинейное распространение света в монослое графена и обнаружили, что монослой графена может поддерживать пространственный оптический солитон TE и TM на оптических частотах из-за внутренней нелинейности графена. Совсем недавно, заменив однослойный графен многослойным графеном, Смирнова и др. [16] исследовали нелинейные свойства многослойной стопки графеновых листов и вывели нелинейные уравнения, описывающие пространственную динамику нелинейных плазмонов. Предыдущие исследования в основном были сосредоточены на влиянии одиночной нелинейности на управление световыми свойствами в графен-диэлектрических структурах. Идея двойного контроля нелинейности была введена в фотонных сверхрешетках на основе графена [18, 19], в которых было достигнуто электрическое и полностью оптическое управление фотонными пучками с глубокой субволновой точностью. Однако двойная нелинейность управления модовыми и дисперсионными свойствами в плазмонной структуре графен-диэлектрик все еще оставляет открытыми многие вопросы. Поэтому в этой статье мы рассматриваем нелинейность графена и диэлектрика одновременно в волноводе графен-диэлектрик-графен и изучаем влияние дуальной нелинейности на свойства связи и дисперсии мод.

Методы

Графен-нелинейный диэлектрический плазмонный волновод схематически показан на рис. 1, графеновая параллельная пластина с проводимостью σ _г помещается в x =± d / 2, где диэлектрик представляет собой среду типа Керра с диэлектрической проницаемостью ε = ε _L + α | E | ² . В нашем анализе графен рассматривается как граница из-за его толщины в масштабе одного атома. Учитывая поперечно-магнитные (TM) ППП, распространяющиеся вдоль z направление с постоянной распространения β и экспоненциально затухает вдоль x направление в воздух и нелинейную среду соответственно.

Принципиальная схема нелинейного плазмонного волновода графен-диэлектрик-графен

Для поляризации TM мы знаем, что есть три компоненты поля E _x , E _z , и H _y . Магнитное поле H = H _y г и электрическое поле E = E _x х + E _z г удовлетворяют уравнениям

где ε ₀ и μ ₀ - электрическая проницаемость и магнитная проницаемость вакуума. Из уравнения. (2) и ε = ε _L + α | E | ² мы можем получить

Подставляя уравнение. (5) в уравнение. (4) имеем

Для кубического уравнения [20, 21]

Дискриминант уравнения. (7) -

Установка \ (b =- \ left ({\ varepsilon} _L + \ alpha {E} _z ^ 2 \ right), \ kern0.5em c =0 \) и \ (d =- \ alpha {\ beta} ^ 2 {H} _y ^ 2 / \ left ({\ omega} ^ 2 {\ varepsilon} _0 ^ 2 \ right) \), легко показать, что дискриминант уравнения (6) встречает

Δ <0 означает, что уравнение. (6) имеет только одно реальное решение. Из метода Кардано [20] мы знаем, что для кубического уравнения Ур. (7) настоящий корень

где p = c - b ² / 3, q = d - до н.э. / 3 + 2 b ³ / 27. Используя уравнение. (10) мы можем получить ε . Замена ε в формуле. Используя реальное решение уравнений (2) и (3), обыкновенные дифференциальные уравнения можно решить численно с помощью релаксационного метода.

Результаты и обсуждения

Из требований непрерывности E _z и H _y , граничные условия в x =± d / 2 удовлетворяют E _{1 z} = E _{2 z} и H _{2 г} - H _{1 г} = σ _г E _z . Поверхностная проводимость графена σ _г определяется формулой Кубо [22], включая вклады межзонных и внутризонных переходов. В ТГц и дальнем инфракрасном диапазоне частот преобладает вклад внутризонных переходов, и поверхностная проводимость может быть упрощена до простого типа Друде как [23]

где e - заряд электрона, μ _c - химический потенциал графена, ω - частота, а τ - время релаксации импульса. Эта модель применима в нижнем пределе температуры ( k _B Т << μ _c ) на низкой частоте ( ℏω ≤ μ _c ). Для условий сильного поля необходимо учитывать нелинейную часть проводимости, и полная проводимость графена равна [16]

где E _τ - тангенциальная составляющая электрического поля и σ ^NL обозначает нелинейную проводимость [16]

где ν _F =0,95 × 10 ⁸ см / с - скорость Ферми.

Что касается графена, то только в ТГц и далекой инфракрасной полосах частот его поверхностная проводимость может быть упрощена до простого типа Друде; поэтому мы выбираем длину падающей волны как λ =10 мкм . Остальные параметры зафиксированы на значениях ε ₁ =1, ε _L =2,25, α =5 × 10 ^{- 16} (м / х) ² [24] E _F =0,27 эв, τ =1,5 пс. Хорошо известно, что в линейных структурах графен-диэлектрик-графен существуют две моды:симметричные и антисимметричные моды соответственно. Далее мы обсудим влияние нелинейности на распределение мод в композитных структурах графен-диэлектрик.

Установка H ₀ в качестве начальной компоненты магнитного поля на падающей границе раздела, путем численного решения уравнений (1, 2 и 3), зависимость начальной напряженности магнитного поля H ₀ от постоянной распространения β приведена на рис. 2. Нормированная постоянная распространения \ ({k} _F =\ sqrt {\ uppi n} \) выражается в единицах импульса Ферми [25], где n =6 × 10 ¹² см ^{- 2} плотность носителей. Сплошные кривые представляют случай, когда учитывается только нелинейность диэлектрика, а пунктирные кривые обозначают случай, когда нелинейность диэлектрика и графена учитывается одновременно. Из рис. 2 видно, что свойства мод для обоих случаев одинаковы. Имеется три ветви, что означает, что нелинейный плазмонный волновод может поддерживать три режима. Однако по сравнению со случаем одиночной нелинейности начальная напряженность поля, по-видимому, уменьшилась для случая двойной нелинейности. Хотя графеновый нелинейный плазмонный волновод может поддерживать три режима, невозможно различить, какая ветвь обозначает симметричный, антисимметричный или асимметричный режим. Чтобы определить модовые свойства каждой ветви, мы строим графики распределения электрического и магнитного поля, связанные с A, B, C и D на рис. 3, соответственно.

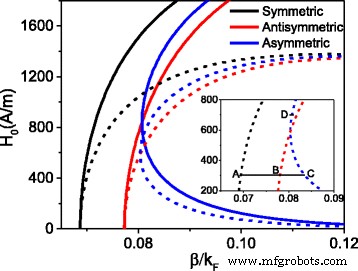
Начальная магнитная напряженность в зависимости от постоянной распространения. Для сплошных кривых : α =5 × 10 ^{- 16} ( м / v ) ² , σ ^NL =0; для штриховых кривых : α =5 × 10 ^{- 16} ( м / v ) ² , σ ^NL =2,19 × 10 ^{- 20} i, горизонтальная сплошная черная линия вспомогательная линия

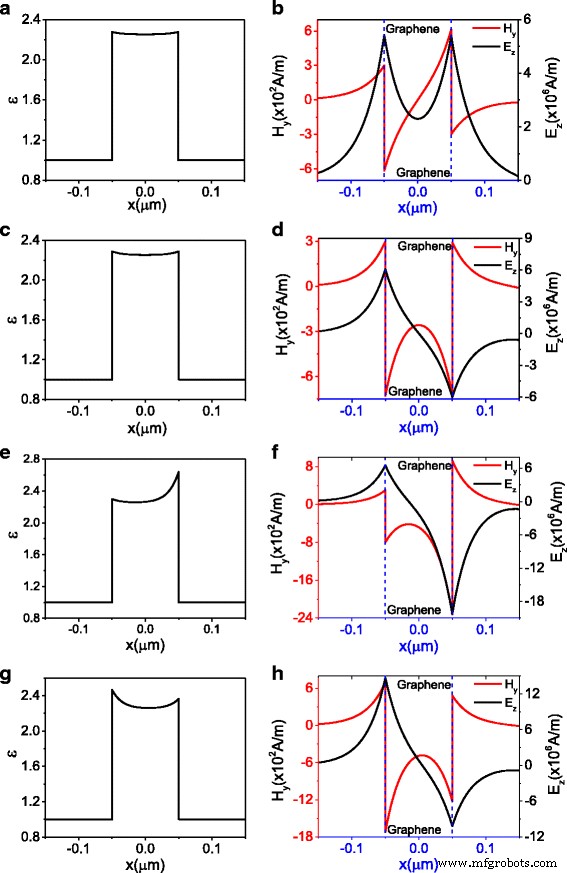
Диэлектрическая проницаемость и распределение мод для магнитной составляющей H _y и электрический компонент E _z . а и b соответствуют точке A ( H ₀ =300, β =6,94 × 10 ^{- 2} к _F ), отмеченные на рис. 2 для симметричных режимов, c и d соответствуют точке B ( H ₀ =300, β =7,81 × 10 ^{- 2} к _F ), отмеченные на рис.2 для антисимметричных режимов, e и е соответствуют точке C ( H ₀ =300, β =8,36 × 10 ^{- 2} к _F ), отмеченные на рис. 2 для асимметричных режимов, и g и h соответствуют точке D ( H ₀ =700, β =8,07 × 10 ^{- 2} к _F )

Для ветви черной пунктирной кривой соответствующая диэлектрическая проницаемость и поля, связанные с A, показаны на рис. 3a, b, на котором распределение диэлектрической проницаемости и электрического поля E _z симметрично. Следовательно, эта ветвь представляет собой симметричный режим. Для ветви красной пунктирной кривой диэлектрическая проницаемость и поля, связанные с B, показаны на рис. 3c, d. Распределение диэлектрической проницаемости остается симметричным; однако распределение электрического поля E _z является антисимметричным, что означает, что эта ветвь является антисимметричной модой. Распределение диэлектрической проницаемости и поля, связанного с C и D, показано на рис. 3e – h. Следует отметить, что распределение соответствующего магнитного поля и электрического поля, связанного с C и D, асимметрично; следовательно, ветвь синей пунктирной кривой представляет асимметричный режим. Между тем асимметричное распределение электрического поля приводит к асимметричному распределению диэлектрической проницаемости.

Далее мы обратим внимание на влияние нелинейности диэлектрика и графена на дисперсионное соотношение. На рисунке 4 показано дисперсионное соотношение для фиксированного начального магнитного поля ( H ₀ =300 А / м) и различные химический потенциал и нелинейные коэффициенты диэлектрика. На рис. 4a – c показано влияние нелинейного коэффициента диэлектрика на дисперсионное соотношение, где учитывается только нелинейность диэлектрика. Когда и нелинейный коэффициент, и нелинейная проводимость равны нулю ( α =0, σ ^NL =0) нелинейная структура вырождается в линейную структуру. На рис. 4а для линейного случая существуют только симметричные и антисимметричные моды. Черная сплошная кривая и сплошная красная кривая представляют симметричную и антисимметричную моды соответственно. Когда коэффициент нелинейности отличен от нуля, в структуре появляется асимметричная мода, такая как ветвь III, показанная на рис. 4b, c. По мере дальнейшего увеличения коэффициента нелинейности влияние коэффициента на дисперсионные свойства становится слабым.

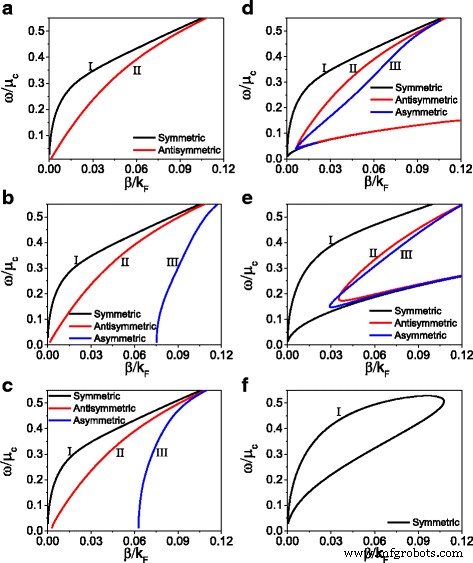
Дисперсионное соотношение для фиксированной начальной магнитной напряженности ( H ₀ =300 А / м) и для различных коэффициентов нелинейности ( a - c ) и для различного химического потенциала ( d - е ). а α =0, μ _c =0,27 эВ, σ _NL =0, b α =5 × 10 ^{- 17} (м / В) ² , μ _c =0,27 эВ, σ _NL =0, c α =5 × 10 ^{- 16} (м / В) ² , μ _c =0,27 эВ, σ _NL =0, d μ _c =0,27 эВ, α =5 × 10 ^{- 16} (м / В) ² , ( e ) μ _c =0,16 эВ, α =5 × 10 ^{- 16} (м / В) ² , и f μ _c =0,10 эВ, α =5 × 10 ^{- 16} (м / В) ²

Далее мы вводим одновременно нелинейность диэлектрика и графена и обсуждаем влияние нелинейности графена на дисперсионное соотношение с фиксированным нелинейным коэффициентом диэлектрика α =5 × 10 ^{- 16} (м / В) ² . Результаты показаны на рис. 4d-f. Сравнивая рис. 4d с рис. 4c, можно заметить, что явление обратного распределения дисперсионного соотношения проявляется во всех трех ветвях. Из уравнения. Из (13) мы знаем, что нелинейностью графена можно управлять, регулируя химический потенциал. По мере дальнейшего увеличения нелинейности графена от μ _c =От 0,27 эВ до μ _c =0,16 эВ, как показано на рис. 4д, точка возврата дисперсионного соотношения смещается вверх. Для большей нелинейности графена (с малым химическим потенциалом μ _c =0,10 эВ), как показано на рис. 4f, появляется только симметричная мода и образует замкнутый контур. Из рис. 4 мы знаем, что, учитывая только нелинейность диэлектрика, дисперсионное соотношение показывает три ветви, которые практически не меняются при увеличении нелинейного коэффициента диэлектрика. Однако, когда мы далее вводим нелинейность графена, появляется явление обратной связи дисперсионного соотношения. Для заданного начального магнитного поля H ₀ и химический потенциал дисперсионное соотношение показывает только симметричный режим с замкнутым контуром.

Выводы

Таким образом, мы исследовали модовые и дисперсионные свойства графен-диэлектрического нелинейного плазмонного волновода. Распределение мод, диэлектрическая проницаемость и дисперсионные соотношения были получены путем численного решения уравнения Максвелла для TM поляризации. По сравнению со случаем, учитывающим только нелинейность диэлектрика, начальная напряженность поля, очевидно, уменьшилась при одновременном рассмотрении нелинейности диэлектрика и графена. Кроме того, двойная нелинейность существенно влияет на дисперсионные свойства волновода. В частности, по мере увеличения нелинейности графена антисимметричная и асимметричная моды сливаются в одну и постепенно исчезают. Следовательно, в случае сильной нелинейности может быть обнаружен только симметричный режим.