Экспериментальные исследования стабильности и естественной конвекции наножидкости TiO2-вода в корпусах с разными углами вращения

Фон

Так как наножидкость готовится, благодаря своим превосходным теплопроводным свойствам [1,2,3], наножидкость широко применяется в области теплопередачи [4,5,6], особенно в области естественной конвекции [7,8,9].

Характеристики теплопередачи естественной конвекции наножидкости численно исследуются многими исследователями. He et al. [10, 11] применили однофазный и двухфазный решеточные методы Больцмана для численного исследования естественной конвективной теплопередачи Al ₂ . О ₃ -водная наножидкость в квадратной полости соответственно. Sheikholeslami et al. [12] исследовали магнитогидродинамические характеристики теплопередачи естественной конвекции горизонтального цилиндрического корпуса с внутренним треугольным цилиндром, заполненным Al ₂ . О ₃ -водная наножидкость методом решеточно-Больцмановского моделирования. Уддин и др. [13] исследовали естественную конвекцию теплопередачи различных наножидкостей вдоль вертикальной пластины, погруженной в пористую среду, на основе модели Дарси-Форххаймера. Meng et al. [14] численно исследовали естественную конвекцию горизонтального цилиндра, заполненного Al ₂ . О ₃ -водная наножидкость. Ахмед и др. [15] использовали метод двухфазной решетки Больцмана для исследования естественной конвекции наножидкости CuO-вода в наклонной камере. Qi et al. [16] численно смоделировали естественную конвекцию наножидкости Cu-Ga в корпусе.

В дополнение к вышеуказанному численному моделированию естественной конвекции наножидкости, все больше и больше исследователей проводят экспериментальные исследования естественной конвекции наножидкости. Ли и др. [17] экспериментально исследовали естественную конвекцию теплопередачи наножидкости ZnO-EG / вода. Hu et al. [18, 19] экспериментально исследовали усиление теплопередачи естественной конвекцией квадратного корпуса, заполненного TiO ₂ . -воды и Al ₂ О ₃ -водяные наножидкости соответственно. Ho et al. [20] экспериментально исследовали естественную конвекцию теплопередачи вертикальных квадратных ограждений разного размера, заполненных Al ₂ . О ₃ -водная наножидкость. Heris et al. [21,22,23] экспериментально исследовали конвективные характеристики теплопередачи различных видов наножидкостей (Cu / вода, Al ₂ О ₃ -воды и CuO-воды) в круглых трубках соответственно. Mansour et al. [24] экспериментально исследовали смешанную конвекцию наклонной трубы, заполненной Al ₂ . О ₃ -водная наножидкость. Chang et al. [25] экспериментально исследовали естественную конвекцию Al ₂ . О ₃ -водная наножидкость в тонких корпусах. Wen et al. [26, 27] экспериментально исследовали конвективные характеристики теплообмена Al ₂ . О ₃ -водные наножидкости и TiO ₂ -водяные наножидкости в условиях ламинарного течения соответственно. Xuan et al. [28] экспериментально исследовали конвекционный теплообмен наножидкости Cu-вода в прямой латунной трубке.

Приведенные выше литературные источники внесли большой вклад в характеристики теплопередачи наножидкости при естественной конвекции. Однако улучшение теплопередачи за счет естественной конвекции в помещениях с разными углами поворота, заполненных наножидкостью, требует дальнейшего изучения. Следовательно, стабильность и характеристики теплопередачи естественной конвекции TiO ₂ -водная наножидкость в корпусах с разными углами поворота ( α =-45 °, α =0 °, α =45 ° и α =90 °) экспериментально исследованы в данной статье.

Метод

Приготовление наножидкости и ее стабильность

TiO ₂ выбран в качестве наночастиц. На рисунке 1 представлены изображения TiO ₂ , полученные с помощью SEM, TEM и XRD. наночастицы при разном увеличении. Из изображений SEM видно, что наночастицы легко собираются вместе, и необходимо принять некоторые меры для приготовления стабильных наножидкостей. Также можно обнаружить, что из изображений ПЭМ, размер частиц составляет около 10 нм, а форма наночастиц плоская. Плоские наночастицы имеют большую площадь теплопередачи, чем сферические наночастицы, при той же массовой доле, что благоприятно сказывается на улучшении теплопередачи. На рисунке 1g показаны рентгенограммы TiO ₂ TTP-A10. наночастица. Как видно, сильные и острые пики предполагают, что TTP-A10 TiO ₂ Образец наночастиц является высококристаллическим. Средний размер частиц образца можно рассчитать по уравнению Шеррера, представленному в формуле. (1). TiO ₂ Размеры наночастиц составляют 6, 9, 14, 20 и 35 нм, рассчитанные по этим значениям дифракционных пиков (111, 200, 021, 202 и 311), а наименьшие размеры наночастиц составляют около 6 и 9 нм на основе значений дифракционных пиков. (111 и 200). Большие размеры наночастиц могут быть вызваны агрегацией наночастиц. Наименьшие значения (6 и 9 нм) могут быть реальными размерами наночастиц, размер нескольких наночастиц может составлять 6 нм, а размер большинства наночастиц может составлять около 9 нм, что более близко к описанию, предоставленному производителем ( 10 нм) и изображения ПЭМ (10 нм).

где k - значение коэффициента формы, а k =0,9; λ - длина волны рентгеновского излучения; и β - линия, расширяющаяся на полную ширину на полувысоте (FWHM) высоты пика в радианах, и θ - угол дифракции Брэгга.

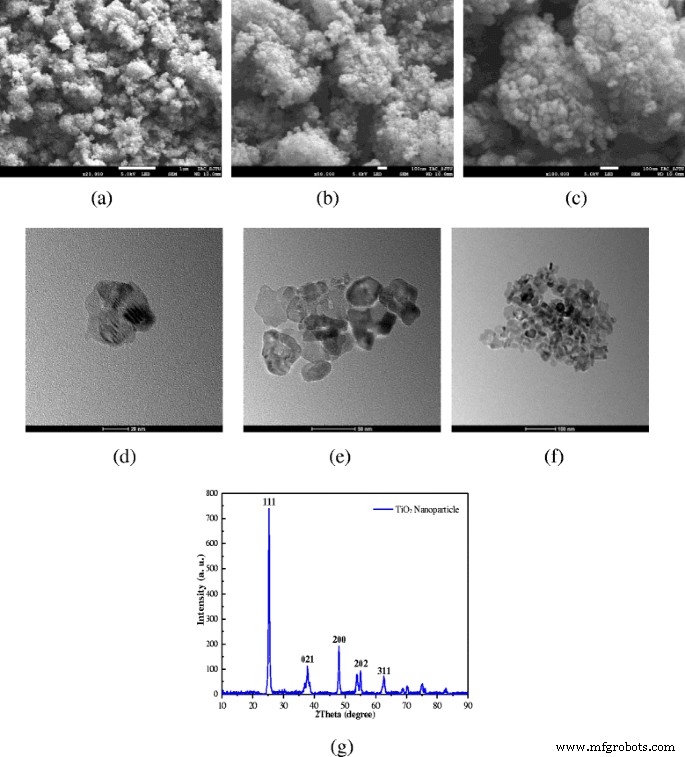
Морфология наночастиц. СЭМ, ПЭМ и XRD изображения TiO ₂ наночастицы при разном увеличении. а SEM × 20000. b SEM × 50000. c SEM × 100000. d ТЕМ 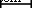20 нм. е ТЕМ 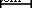50 нм. е ТЕМ 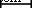100 нм. г XRD

TiO ₂ -водная наножидкость с различными массовыми долями наночастиц (мас.% =0,1%, мас.% =0,3% и мас.% =0,5%) готовится двухэтапным методом, который показан на рис. 2. Время механического перемешивания составляет половину час для каждого из подэтапов, а время обработки ультразвуком составляет 40 мин. Таблица 1 показывает информацию о некоторых материалах и оборудовании для приготовления наножидкостей. На рисунке 3 показан TiO ₂ . -водная наножидкость перед укладкой и через 72 ч. Видно, что наночастицы мало осаждаются в пробирке, а наножидкость, приготовленная в этой статье, показывает хорошую стабильность.

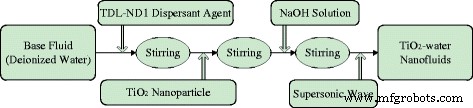
Приготовление наножидкостей. Методика приготовления TiO ₂ -водные наножидкости двухступенчатым методом

Наблюдение за стабильностью TiO ₂ -водная наножидкость. TiO ₂ -водная наножидкость в разное время. а Перед укладкой. б Через 72 ч

В дополнение к исследованию того, есть ли отложения наночастиц в пробирке, были изучены эффекты пропускания ( τ ) наножидкости на ее стабильность. На рисунке 4 показан коэффициент пропускания ( τ ) изменения TiO ₂ -водная наножидкость (вес.% =0,5%) с разными значениями pH и дозами ( м ) диспергатора. Коэффициент пропускания измеряется спектрофотометром в ультрафиолетовой видимой области (UV-1800 (PC)). Как мы знаем, если наночастицы равномерно распределятся в воде, наночастицы будут отражать больше всего света и иметь высокий коэффициент отражения (низкий коэффициент пропускания). Следовательно, стабильность наножидкости обратно пропорциональна коэффициенту пропускания, а стабильная наножидкость имеет низкий коэффициент пропускания. Из рис. 4 видно, что наножидкость с m =6 мас.% И pH =8 имеет самый низкий коэффициент пропускания и лучшую стабильность. Наножидкости с различными массовыми долями наночастиц в этом эксперименте готовятся на м =6 мас.% И pH =8, что может гарантировать стабильность наножидкостей.

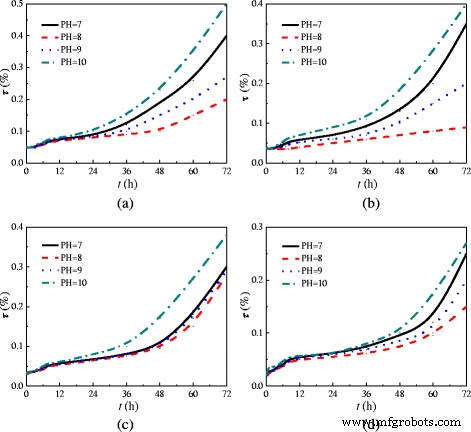
Коэффициент пропускания TiO ₂ -водная наножидкость. Коэффициент пропускания ( τ ) изменения TiO ₂ -водная наножидкость (вес.% =0,5%) при различных значениях pH со временем ( h ) в разных дозах ( м ) диспергатора. а м =5% масс. б м =6 мас.%. c м =7% масс. г м =8 мас.%

Экспериментальная система

На рис. 5 показаны схематические диаграммы трех экспериментальных установок. Размеры трех прямоугольных корпусов:10 см (ширина) × 20 см (высота), 5 см (ширина) × 20 см (высота) и 20 см (ширина) × 20 см (высота). Ширина и высота определяются как W и H соответственно, и соотношение сторон ( A ) корпуса определяется как A =W / H . Левая стенка (медная пластина) корпуса нагревается силиконовой нагревательной пластиной, подключенной к источнику постоянного тока. Правая стенка (медная пластина) корпуса охлаждается охлаждающей водой в небольшой полости (материал также медь), соединенной с водяной баней постоянной температуры. Температуры двух сторон корпуса измеряются шестью термопарами, подключенными к прибору для сбора данных (Agilent 34972A). Внешний изоляционный слой используется для предотвращения потери тепла.

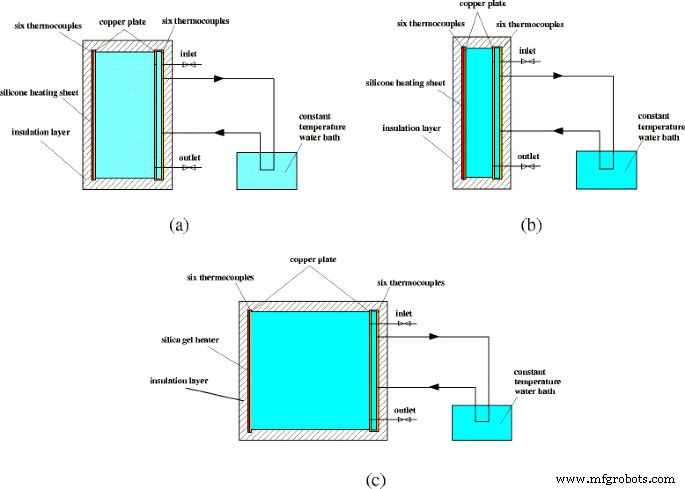
Принципиальные схемы экспериментальных наборов. Схематические диаграммы трех экспериментальных наборов с различным соотношением сторон. а А =1:2. б А =1:4. c А =1:1

Характеристики теплопередачи естественной конвекции двух кожухов с разными углами поворота ( α =-45 °, α =0 °, α =45 ° и α =90 °), заполненный TiO ₂ -водяные наножидкости исследуются в данной статье. Для корпуса с α =-90 °, верхняя стенка является горячей стенкой, а нижняя стенка - холодной стенкой, а теплопередача в корпусе в основном является теплопроводностью. Однако в рукописи в основном исследуется естественная конвекция теплопередачи наножидкости в корпусе, следовательно, в корпусе с α =−90 ° не рассматривается в данной рукописи. На рисунке 6 представлена ​​принципиальная схема корпусов с разными углами поворота.

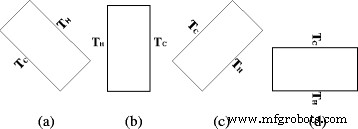
Принципиальная схема углов поворота. Принципиальная схема шкафов с четырьмя разными углами поворота. а α =-45 °. б α =0 °. c α =45 °. г α =90 °

Обработка данных

Мощность Q Силиконовый нагревательный лист обеспечивает следующее:

где U и я - напряжение и электричество источника постоянного тока соответственно.

Эффективная мощность Q _net выглядит следующим образом:

где Q _потеря - потери тепла, измеренные счетчиком теплового потока.

Температура стороны медной пластины рядом с силиконовым нагревательным листом \ ({T} _ {\ mathrm {H}} ^ {*} \) следующая:

где T ₁ , Т ₂ ,…, T ₆ - температуры термопар.

Температура стороны медной пластины (левая сторона корпуса) рядом с наножидкостью T _H выглядит следующим образом:

где δ =0,005 м - толщина медной пластины, A площадь медной пластины, λ _w - теплопроводность медной пластины.

Температура стороны медной пластины (правая сторона корпуса) рядом с изоляционным слоем T _C ^∗ выглядит следующим образом:

где T ₇ , Т ₈ ,…, T ₁₂ - температуры термопар в правой части корпуса.

Когда достигается состояние теплового равновесия, температура охлаждающей воды совпадает с температурой стороны медной пластины рядом с охлаждающей водой. Температура стороны медной пластины (правая сторона корпуса) рядом с наножидкостью T _C можно рассчитать следующим образом:

Качественная температура T _м определяется следующим образом:

Коэффициент конвективной теплоотдачи h выглядит следующим образом:

Число Нуссельта определяется следующим образом:

где λ _f - теплопроводность жидкости в корпусе.

Анализ неопределенности

Формула передачи погрешности коэффициента конвективной теплоотдачи имеет следующий вид [19]:

Формула передачи ошибки числа Нуссельта выглядит следующим образом [19]:

Основываясь на уравнениях. Согласно (10) и (11) ошибки коэффициентов конвективной теплоотдачи и числа Нуссельта в этом эксперименте составляют 5,65 и 6,34% соответственно. Было обнаружено, что ошибки экспериментальных наборов невелики, что может гарантировать надежность и точность экспериментальных результатов.

Результаты и обсуждения

Проверка эксперимента

Перед исследованием наножидкости необходима валидация эксперимента. На рисунке 7 показано сравнение чисел Нуссельта между экспериментальными результатами для воды и результатами опубликованных литературных источников для корпусов с A =1:2, А =1:4 и A =1:1. Максимальные ошибки для корпусов с A =1:2, А =1:4 и A =1:1 составляют 8,4, 9,5 и 8,1% соответственно. Можно обнаружить, что экспериментальные результаты хорошо согласуются с результатами опубликованных литературных источников [20, 29], что подтверждает точность и надежность экспериментальной системы.

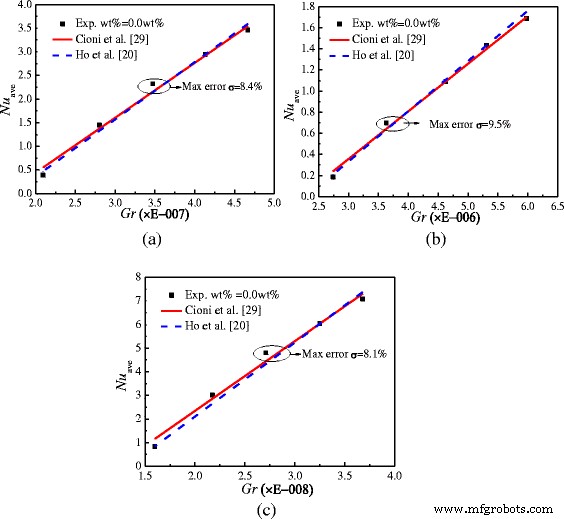
Проверка набора экспериментов. Сравнение чисел Нуссельта между экспериментальными результатами и опубликованной литературой в приложениях с двумя различными соотношениями сторон. а А =1:2. б А =1:4. c А =1:1

Вложение с A =1:2

Влияние углов поворота на характеристики теплопередачи естественной конвекции TiO ₂ -водяные наножидкости обсуждаются в этой статье. На рисунке 8 представлены изменения средних чисел Нуссельта при углах поворота корпуса с A =1:2. Из рис. 8 видно, что числа Нуссельта сначала увеличиваются, а затем уменьшаются с увеличением углов поворота. Корпус с углом поворота α =0 ° имеет наибольшее число Нуссельта, за которым следует корпус с углами поворота α =45 ° и α =90 °, корпус с углом поворота α =−45 ° имеет наименьшее число Нуссельта. Теплопроводность становится все более важной при уменьшении угла поворота ( α ≤ −90 °), и передача тепла почти теплопроводность, когда угол поворота уменьшается до α =-90 °. Когда горячая стена располагается вверху, а холодная стена - внизу корпуса ( α =−90 °), плавучесть направлена ​​вверх, но верхняя стенка препятствует движению жидкости вверх. Движение наножидкости в корпусе невелико, и основной теплопередачей является теплопроводность, которая вызывает небольшое число Нуссельта. Корпус с α =−45 ° ближе к корпусу с α =-90 ° и показывает наименьшее число Нуссельта по сравнению с другими углами вращения. Для корпусов с углами поворота α =45 ° и α =90 °, жидкость у нижней горячей стенки нагревается и движется вверх, а жидкость у верхней холодной стенки охлаждается и движется вниз. Направления горячей и холодной жидкости противоположны и препятствуют естественной конвекции теплопередачи, что приводит к более низкому числу Нуссельта по сравнению с корпусом с α =0 °, но более высокое число Нуссельта по сравнению с корпусом с α =-45 °. Также видно, что разница между различными углами поворота увеличивается с увеличением мощности нагрева. Это связано с тем, что влияние углов вращения играет основную роль на теплопередачу при низкой мощности нагрева, а влияние конвекции на теплопередачу невелико. Однако интенсивность конвективной теплопередачи увеличивается с увеличением мощности нагрева и играет основную роль в передаче тепла при высокой мощности нагрева, что вызывает большие различия между различными углами поворота при высокой мощности нагрева по сравнению с углами поворота при низкой мощности нагрева.>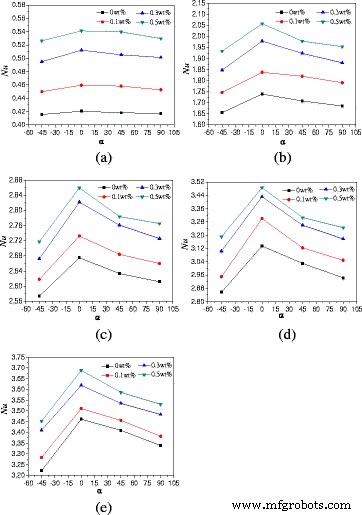

Изменения чисел Нуссельта с углами поворота ( A =1:2). Изменение среднего числа Нуссельта наножидкости с углами поворота оболочки ( A =1:2) при разных мощностях нагрева. а Q =1 Вт. b Q =5 Вт. c Q =10 Вт. d Q =15 Вт. e Q =20 Вт

Помимо углов вращения, обсуждается также влияние массовой доли наночастиц на естественную конвекционную теплопередачу. На рис. 9 показано изменение средних чисел Нуссельта в зависимости от массовой доли наночастиц. Можно обнаружить, что числа Нуссельта увеличиваются с увеличением массовой доли наночастиц. Для тепловой мощности Q =1 Вт и α =0 °, TiO ₂ -водная наножидкость с вес.% =0,1%, вес.% =0,3% и вес.% =0,5% может улучшить теплопередачу на 9,3, 21,8 и 28,7% по сравнению с водой, соответственно. Коэффициент усиления уменьшается с увеличением мощности нагрева. Для тепловой мощности Q =20 Вт и α =0 °, TiO ₂ -водная наножидкость с вес.% =0,1%, вес.% =0,3% и вес.% =0,5% может улучшить теплопередачу на 1,4, 4,6 и 6,6% по сравнению с водой, соответственно. Интенсивность турбулентности играет важную роль при высокой мощности нагрева, а влияние массовой доли наночастиц на теплопередачу становится незначительным.

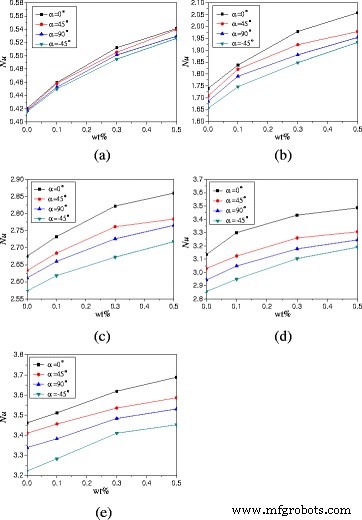
Изменение чисел Нуссельта в зависимости от массовой доли наночастиц ( A =1:2). Средние числа Нуссельта изменения наножидкости в корпусе ( A =1:2) с массовой долей наночастиц при различной мощности нагрева. а Q =1 Вт. b Q =5 Вт. c Q =10 Вт. d Q =15 Вт. e Q =20 Вт

В данной работе исследуется влияние тепловых мощностей на естественную конвекционную теплопередачу. На рисунке 10 показано изменение средних чисел Нуссельта в зависимости от мощности нагрева. Для α =0 °, TiO ₂ -водная наножидкость при Q =5 Вт, Q =10 Вт, Q =15 Вт и Q =20 Вт может улучшить теплопередачу на 280,2, 428,4, 544,1 и 581,5% по сравнению с Q =1 Вт. Высокая мощность нагрева увеличивает интенсивность турбулентности и улучшает теплопередачу.

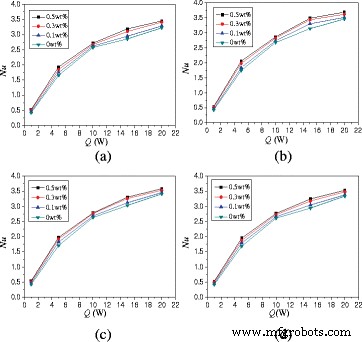
Изменение чисел Нуссельта в зависимости от мощности нагрева ( A =1:2). Средние числа Нуссельта изменения наножидкости в корпусе ( A =1:2) с мощностью нагрева при разных углах поворота. а α =-45 °. б α =0 °. c α =45 °. г α =90 °

Вложение с A =1:4

Чтобы исследовать влияние соотношения сторон корпуса на теплопередачу, были изучены характеристики теплопередачи естественной конвекции корпуса с A =1:4 заполнен TiO ₂ -водная наножидкость. На рисунке 11 показано изменение средних чисел Нуссельта в зависимости от углов поворота оболочки. Можно получить, что аналогичный вывод типа A =1:2, что числа Нуссельта сначала увеличиваются, а затем уменьшаются с увеличением углов поворота. Например, для наножидкости с масс.% =0,5% различия между A =1:4 и A =1:2 означает, что коэффициенты улучшения (от 6,5 до 20,7%) числа Нуссельта в корпусе ( A =1:4, α =0 °) по сравнению с корпусом ( A =1:4, α =-45 °) выше, чем коэффициенты увеличения (от 2,85 до 9,3%) числа Нуссельта в корпусе ( A =1:2, α =0 °) по сравнению с корпусом ( A =1:2, α =-45 °).

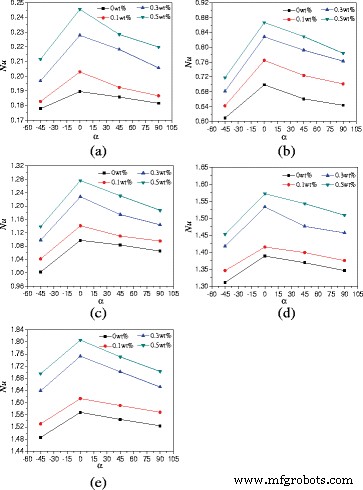
Изменения чисел Нуссельта с углами поворота ( A =1:4). Средние числа Нуссельта изменения наножидкости с углами поворота оболочки ( A =1:4) при разных мощностях нагрева. а Q =1 Вт. b Q =5 Вт. c Q =10 Вт. d Q =15 Вт. e Q =20 Вт

На рисунке 12 представлены изменения средних чисел Нуссельта в зависимости от массовой доли наночастиц. Для тепловой мощности Q =1 Вт и α =0 °, TiO ₂ -водная наножидкость с вес.% =0,1%, вес.% =0,3% и вес.% =0,5% может улучшить теплопередачу на 7,1, 20,2 и 29,5% по сравнению с водой, соответственно. Коэффициент усиления уменьшается с увеличением мощности нагрева. Для тепловой мощности Q =20 Вт и α =0 °, TiO ₂ -водная наножидкость с вес.% =0,1%, вес.% =0,3% и вес.% =0,5% может улучшить теплопередачу на 2,9, 11,8 и 15,1% по сравнению с водой, соответственно.

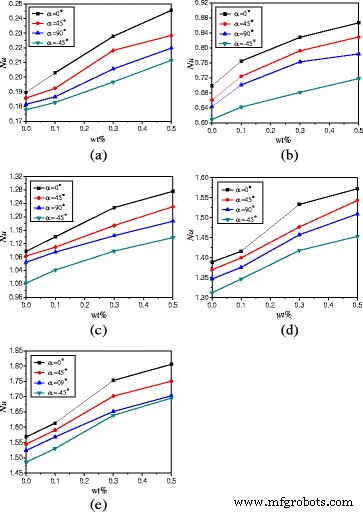
Изменение чисел Нуссельта в зависимости от массовой доли наночастиц ( A =1:4). Средние числа Нуссельта изменения наножидкости в корпусе ( A =1:4) с массовой долей наночастиц при различной мощности нагрева. а Q =1 Вт. b Q =5 Вт. c Q =10 Вт. d Q =15 Вт. e Q =20 Вт

На рисунке 13 показано изменение средних чисел Нуссельта в зависимости от мощности нагрева. Среднее число Нуссельта наножидкости может быть увеличено на 242,4% ~ 701,5% по сравнению с водой при тепловой мощности Q =1 Вт. Для α =0 °, TiO ₂ -водная наножидкость с вес.% =0,5% при Q =5 Вт, Q =10 Вт, Q =15 Вт и Q =20 Вт может улучшить теплопередачу на 253,0, 419,9, 540,3 и 635,6% по сравнению с Q =1 Вт соответственно.

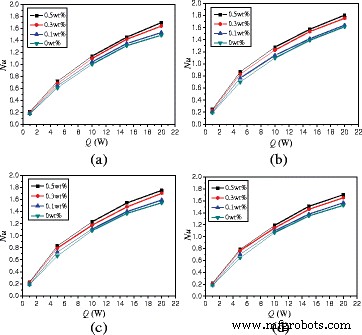
Изменение чисел Нуссельта в зависимости от мощности нагрева ( A =1:4). Средние числа Нуссельта изменения наножидкости в корпусе ( A =1:4) с мощностью нагрева при разных углах поворота. а α =-45 °. б α =0 °. c α =45 °. г α =90 °

Сравнение между A =1:2, А =1:4 и A =1:1

Из-за ограничения длины этого документа результаты приложения с A =1:1 приведены только на рис. 14, а влияние различных углов вращения, массовых долей наночастиц и мощности нагрева на теплопередачу можно показать на рис. 14. Чтобы сравнить характеристики теплопередачи кожухов с А =1:2, А =1:4 и A =1:1, на рис. 14 показано сравнение средних чисел Нуссельта между A =1:2, А =1:4 и A =1:1 при разных углах поворота. Обнаружено, что числа Нуссельта увеличиваются с увеличением соотношения сторон корпуса. Числа Нуссельта корпуса ( A =1:1 и A =1:2) может быть увеличено на 190,6% ~ 224,4% и 103,6% ~ 172,0% по сравнению с числами Нуссельта корпуса ( A =1:4) при тех же условиях соответственно. Для Q =1 Вт и α =0 °, например, наножидкость с масс.% =0,5%, масс.% =0,3%, масс.% =0,1% и масс.% =0,0% в корпусе с A =1:2 может улучшить теплопередачу на 120,4, 124,9, 126,5 и 121,9% по сравнению с таковым в кожухе с A =1:4. Коэффициент усиления уменьшается с увеличением мощности нагрева. vFor Q =20 Вт и α =0 °, наножидкость с масс.% =0,5%, масс.% =0,3%, масс.% =0,1% и масс.% =0,0% в корпусе с A =1:2 может улучшить теплопередачу на 104,2, 106,5, 117,6, 120,7% по сравнению с таковой в кожухе с A =1:4. Также обнаружено, что увеличение числа Нуссельта от вес.% =0,1% до вес.% =0,3% больше, чем от вес.% =0,3% до вес.% =0,5%. Это связано с тем, что увеличение теплопроводности играет основную роль в передаче тепла от вес.% =0,1% до вес.% =0,3%, что вызывает большое улучшение. Но увеличение вязкости начинает играть основную роль в теплопередаче от вес.% =0,3% до вес.% =0,5%, что вызывает небольшое увеличение. Так как на рис. 14 можно охватить все экспериментальные результаты, подробные результаты на рис. 14 показаны в таблицах 2, 3 и 4.

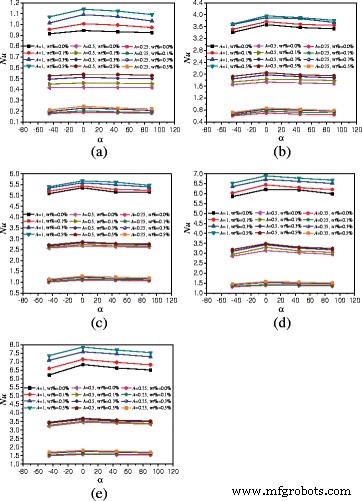
Nusselt numbers comparison between different aspect ratios. Comparison of average Nusselt numbers of nanofluid in different aspect ratios (A  = 1:1, A  = 1:2, and A = 1:4) and rotation angle enclosures at different heating powers. а Q  = 1 W. b Q  = 5 W. c Q  = 10 W. d Q  = 15 W. e Q  = 20 W

Conclusions

The stability and natural convection heat transfer characteristics of the two enclosures with different rotation angles (α  = −45°, α  = 0°, α  = 45°, and α  = 90°) filled with TiO₂ -water nanofluid are experimentally investigated. Some conclusions are obtained as follows:

1. (1)

   TiO₂ -water nanofluid with m  = 6 wt% and pH = 8 has the lowest transmittance and has the best stability.

2. (2)

   The enclosure with rotation angle α  = 0° has the highest Nusselt number followed by the enclosure with rotation angles α  = 45° and α  = 90°; the enclosure with rotation angle α  = −45° has the lowest Nusselt number.

3. (3)

   There is a higher heat transfer performance in a bigger aspect ratio enclosure. The Nusselt numbers of enclosure (A  = 1:1 and A  = 1:2) can be enhanced by 190.6% ~ 224.4% and 103.6% ~ 172.0% compared with the Nusselt numbers of enclosure (A  = 1:4) at the same conditions.

4. (4)

   Nusselt numbers increase with nanoparticle mass fractions, but the enhancement ratio decreases with the heating power.

5. (5)

   Average Nusselt numbers increase with the heating power. Average Nusselt numbers of nanofluid can be enhanced by 701.5% compared with water at the best.