Свойства продольных электромагнитных колебаний в металлах и их возбуждение на плоских и сферических поверхностях

Фон

Облучение плоской металлической поверхности фемтосекундными лазерными импульсами часто приводит к образованию лазерно-индуцированных периодических поверхностных структур (LIPSS) [1]. Помимо LIPSS наблюдалась сверхтонкая рябь, называемая высокочастотной LIPSS (HSFL) [1, 2]. Пространственные периоды HSFL значительно меньше длины волны излучения λ ₀ . Например, для алюминия этот период оценивается в диапазоне от 20 до 200 нм при λ ₀ =0,8 мкм м [2, 3]. В то время как ориентация ряби в обычных LIPSS была перпендикулярна поляризации лазерного излучения, ориентация HSFL часто была перпендикулярна, а иногда и параллельна поляризации. Подобные ВСФЛ формировались на поверхностях прозрачных диэлектриков, полупроводников и металлов. Происхождение HSFL объяснялось различными механизмами, такими как генерация второй гармоники, участие определенных типов плазмонных мод, самоорганизация и усиление локального поля во время неоднородного пробоя в диэлектрических материалах [2, 3].

Целью этого исследования является поиск волнового процесса, который мог бы создать модель с коротким периодом Λ ≪ λ ₀ . Мы исследуем свойства продольных (L) электромагнитных волн в металлах, также известных как плазменные волны. Наше исследование состоит из следующих новых шагов. Во-первых, мы начали наши исследования с определения пространственной дисперсии диэлектрической проницаемости. Как показано ниже, общее определение бесполезно, если исследуемая среда не является однородной и бесконечной. Поэтому мы предлагаем новую концепцию пространственно-дисперсионной диэлектрической проницаемости ε . Эта функция устанавливает прямую пропорциональность между двумя векторными полями, E ( г , ω ) и D ( г , ω ), но не амплитуды E ( к , ω ) и D ( к , ω ) плоских волн. Следовательно, величина ε зависит от квадрата волнового числа, k ² , параметр векторного уравнения Гельмгольца для электрического поля E ( г , ω ), но не волновой вектор k плоских волн. Затем, чтобы получить такую ​​новую функцию, мы определили реакцию электронов проводимости на электромагнитную моду, решив уравнение переноса Больцмана, записанное в приближении времени релаксации. Получены так называемые поперечная и продольная диэлектрические функции Линдхарда. Далее мы обнаружили, что продольная функция Линдхарда и гораздо более простая гидродинамическая функция близки в широком диапазоне параметров. Для иллюстрации теории было рассмотрено ослабление света серебряными и золотыми наносферами. Мы впервые показываем, что нелокальная теория Ми объясняет голубой сдвиг, уширение и возможное исчезновение плазмонных резонансов, наблюдаемых при уменьшении размера наносфер из благородных металлов. Наконец, недавно разработанная теоретическая модель была применена для изучения возможности участия продольных мод в формировании лазерно-индуцированных поверхностных структур. Для этого мы модифицировали теорию Френеля с учетом прошедших продольных волн.

Методы

Для определения электромагнитных полей в кусочно-однородных средах применялась классическая теория электромагнитного поля. Электрическое поле E в каждой однородной области неоднородной среды предполагалось решение векторного уравнения Гельмгольца (VHE):

где Δ - оператор Лапласа.

Как обычно, тангенциальные компоненты электрического E и магнитный H поля непрерывны через границы СМИ. Кроме того, мы учли, что электроны удерживаются в металле; следовательно, следующее дополнительное граничное условие (ABC) для нормальной составляющей плотности тока j на металлической поверхности S было использовано:( j н ) | _{r ∈ S} =0.

Чтобы определить ток проводимости в металле, мы решили уравнение переноса Больцмана (BTE), записанное в приближении времени релаксации:

где f - одночастичная функция распределения в фазовом пространстве ( r , v ), v - микроскопическая скорость электронов, e и м - заряд и масса электрона соответственно, B магнитная индукция, f ₀ - равновесная функция распределения, а τ время релаксации.

Ниже мы выводим формулы для пространственно-дисперсионных диэлектрических функций. Затем мы используем их для изучения отражения света от плоской металлической поверхности и рассеяния света на наносфере из благородного металла.

Результаты и обсуждение

Пространственная дисперсия ε в неоднородной среде

В литературе пространственно-дисперсионная диэлектрическая проницаемость ε определяется следующим соотношением [4–6]:

где ε ₀ - электрическая постоянная, D ( ω , г ) - амплитуда колебаний вектора смещения с угловой частотой ω в точке r , и E ( ω , г ^′ ) амплитуда колебаний электрического поля в точке r ^′ . Преобразования Фурье уравнения (3) дать уравнение

где пространственно-дисперсионный ε ( ω , k ) зависит от волнового вектора k плоской электромагнитной волны. По нашему мнению, уравнение. (3) не является неоднозначным только в бесконечном однородном объеме, но мы имеем дело с кусочно-неоднородной системой, в которой необходимо учитывать границы и k не совпадают на разных носителях.

В нашем подходе не используется разложение электромагнитных волн на плоские волны. Пространственно-дисперсионная диэлектрическая проницаемость определяет соотношение между D ( ω , г ) и частное решение векторного уравнения Гельмгольца. (1):

Здесь E ( ω , г ) обозначает распределение электрического поля, а не просто вектор E в точке r .

Продольные и поперечные диэлектрические функции

Диэлектрическая проницаемость металлов обычно выражается через проводимость σ [4]:

где ε _g является частью диэлектрической функции, учитывающей поляризацию твердого тела; ε _g =1 для простого металла. Для определения σ , мы рассчитали плотность тока

где \ (\ mathrm {d} \ mathbf {v} =\ frac {v} {m} \, \ mathrm {d} \ epsilon \, \ mathrm {d} \, \ Omega, \) d Ω =грех θ г θ d ϕ , v , θ , ϕ - сферические координаты скорости. В отличие от предыдущих исследований, мы не вводили волновой вектор k но нашел решение BTE в виде бесконечной серии, содержащей операторы v ∇ действует на v E :

где Γ =1 / τ . Затем f ₀ была аппроксимирована распределением Ферми-Дирака при нулевой температуре и после интегрирования по ε в формуле. (7), мы получили

где \ (\ omega _ {\ mathrm {p}} ^ {2} =\ frac {e ^ {2} \, n_ {e}} {m \, \ varepsilon _ {0}}, \) ω _p - плазменная частота, \ (\ mathbf {u} =\ frac {\ mathbf {v}} {v} \) - единичный вектор в направлении v , \ (l =\ frac {v _ {\ mathrm {F}}} {- i \ omega + \ Gamma}, \) v _F - скорость Ферми. Далее мы вычислили интегралы

где n натуральное число. Следующая зависимость j на произвольном электрическое поле E наконец-то получено

Есть два типа решений уравнения. (1), бездивергентные, удовлетворяющие уравнению ∇ · E =0 и без вращения, которые удовлетворяют уравнению

Для плоской волны с E ∝ ехр [ я ( к г - ω т )], Уравнение. (14) преобразуется в соотношение k × E =0, что показывает, что волна является продольной (L). Для моделирования процессов в сферических телах удобно использовать векторные сферические гармоники L , M , и N как полный набор ортогональных функций. В этом случае уравнение. (14) определяет гармоники L . Волновое число волн L и L режим определяется следующим законом дисперсии

Из уравнений. (6) и (13) мы находим, что решения уравнения (1) удовлетворяющий ограничению уравнения. (14) дают следующую продольную диэлектрическую проницаемость

где Φ - функция Phi Лерха,

\ (a =\ frac {k v _ {\ mathrm {F}}} {\ omega + i \ Gamma} \).

Полученная диэлектрическая проницаемость отличается от определенной Кливером и Фуксом [7] только обозначениями:

Личность

позволяет переписать уравнение. (18) следующим образом

В случае Γ =0, эта формула принимает форму уравнения, полученного Климонтовичем и Силиным [8], которые исследовали демпинг Ландау в вырожденной плазме (см. [9], [10, уравнение (40.17)] и [11]). Диэлектрическая проницаемость эквивалентных уравнений. (16), (18) и (20) обычно называют диэлектрической функцией Линдхарда (со ссылкой на [12]), хотя эта функция была впервые получена Климонтовичем и Силиным [8].

Поперечная диэлектрическая проницаемость Линдхарда [7] может быть найдена по формуле. (13) когда ∇ · E =0. В реальном случае v _F к ≪ ω , сводится к диэлектрической проницаемости Друде

Эта функция согласуется с экспериментальными данными для многих металлов [13]. Если | a | <1 продольная диэлектрическая проницаемость (16) упрощается до гидродинамической диэлектрической проницаемости:

Отражение плоской электромагнитной волны от плоской металлической поверхности

Граничные условия

В этом разделе мы определяем направление волнового вектора k ^L и амплитуда L-волны, возбуждаемой в металле при отражении плоской электромагнитной волны от плоской металлической поверхности.

Рассмотрим плоскую волну, падающую на границу раздела диэлектрик-металл z =0 с волновым вектором, лежащим в xz самолет. Электрическое поле в диэлектрической среде 1 состоит из падающих E _я и отраженный E _r волн, поле в металле 2 имеет проходящую поперечную E _t и, в некоторых случаях, продольный E ^L компоненты. Согласно граничным условиям Максвелла поперечные компоненты векторов электрического и магнитного поля непрерывны в плоскости z =0. Кроме того, электроны не выбрасываются из металла; следовательно, нормальная составляющая плотности электрического тока равна нулю в z =0,

были \ (\ hat {\ mathbf {z}} \) - единичный вектор в направлении z ось.

Все члены в граничных условиях Максвелла должны иметь одинаковую зависимость от x и y . Это требование имеет несколько последствий. Во-первых, можно установить, что L-волны могут быть возбуждены только в случае p-поляризации, когда электрический вектор падающей волны E ^{( я )} параллельно плоскости падения. Другими словами, плазмон-поляритоны могут генерироваться поперечной магнитной (TM) волной. Эффект почти такой же, как в металлической сфере [14]. Во-вторых, формулы, подобные закону Снеллиуса, могут быть получены из условий

где индексы 1 x и 2 x обозначают x -проекции векторов в средах 1 и 2 соответственно, θ ₁ угол падения.

Коэффициенты отражения и передачи

Определим поле, образованное плоской p-поляризованной электромагнитной волной, падающей на плоскую металлическую поверхность. Компоненты электрического и магнитного полей удобно выражать через x компонент E ^{( я )} , а именно E x (г) =- г E x (i) для отраженной волны E x (t) = t E x (i) для прошедшей поперечной волны, и

для прошедшей продольной волны здесь r коэффициент отражения, t и t _L коэффициенты передачи.

Из граничных условий Максвелла и ABC уравнения. (23) записывается в следующей форме

мы получили

При δ =0, коэффициент r становится коэффициентом Френеля отражения p-поляризованной волны (см., например, уравнение (2.49) в [4]). При тех же условиях t не является коэффициентом пропускания Френеля, поскольку наши определения t и r отличаются от френелевских.

Погасание света металлической наносферой

В предыдущей статье один из авторов обобщил теорию Лоренца-Ми с учетом ABC уравнения (1). (23). Аналог коэффициента Френеля r , коэффициент Ми b _l для отраженного режима TM l -й заказ был обнаружен

где

ψ _l и ζ _l - функции Риккати-Бесселя и Риккати-Ганкеля порядка l , соответственно; j _l - сферическая функция Бесселя, штрих обозначает производную функции по ее аргументу.

Сравним предсказания классической и обобщенной теорий Лоренца-Ми с экспериментальными данными. В [15] Хильгер, Тенфельде и Крейбиг исследовали спектры экстинкции наночастиц серебра, нанесенных на диэлектрические поверхности. На первом этапе исследования ученые генерировали пучки частиц серебра со средним диаметром 2, 3,5 и 4 нм, определили распределение частиц по размерам для одного из пучков, зарегистрировали спектры экстинкции и оценили параметр A =0,25 феноменологической формулы Γ = Γ _b + A v _F / R , где Γ _b - скорость релаксации объемного металла для серебряных сфер в вакууме. Сначала мы рассчитали спектры экстинкции пучка серебряных сфер со средним диаметром 〈 D 〉 =2 нм и экспериментальное распределение размеров, которое охватывает область от D =От 1 до D =4 нм. Наша теория не содержит настраиваемых параметров. Для определения диэлектрических функций использовалась таблица показателя преломления массивного серебра, предложенная Линчем и Хантером [16] (см. Рис. 1). Мы также применили уравнения. (16), (21) и (22) с ω _p =9,17 эВ, Γ _b =0,021 эВ, v _F =1,39 × 10 ⁶ м / с и A =0,25. Результаты расчетов и экспериментальный спектр представлены на рис. 2.

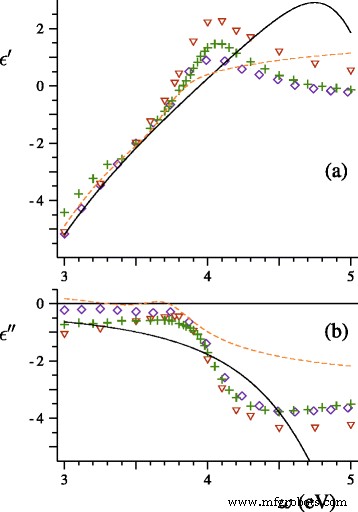
Реальный ( а ) и мнимой ( b ) части диэлектрической функции серебра согласно Джонсону и Кристи () [20], Линчу и Хантеру (+) [16], Веберу (△) [21], Хао и Нордландеру ( пунктирная линия ) [22], Драчев и др. ( сплошная линия ) [23]

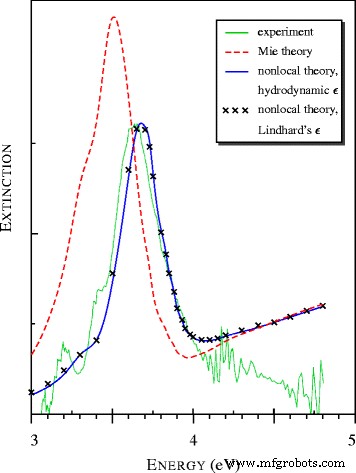
Спектры поглощения света частицами серебра нанометрового размера, наблюдаемые в [15] и рассчитанные с использованием локальной и нелокальной моделей. Все теоретические спектры представлены в общепринятых относительных единицах

Теоретические спектры на рис. 2 были рассчитаны с использованием диэлектрических функций Климонтовича-Силина-Линдхарда и значительно более простых гидродинамических диэлектрических функций. Удивительно, что оба вычисления дали близкие результаты, хотя | a |> 1 в области плазмонного резонанса.

Для серебряных сфер нанометрового размера максимум в спектре экстинкции, называемый резонансом Фрелиха [17], плазмона и поверхностного плазмон-поляритона (SPP) [15], смещается от 3,5 до 3,65 эВ [18]. Нелокальная модель прекрасно согласуется с экспериментальными данными, тогда как локальная (Ми) теория дает максимум при ω 3,5 эВ (см. Рис. 2 и таблицу 1).

В пользу расчета синего сдвига плазмонного резонанса можно привести следующие соображения. В электростатическом приближении только b ₁ вносит вклад в сечение экстинкции Q _ext и уравнение. (30) можно упростить, используя следующие приближения

$$ \ frac {k_ {2} R \, \ psi_ {l} ^ {\ prime} (k_ {2} R)} {\ psi_ {l} (k_ {2} R)} \ simeq l + 1; \, \, \, \ frac {k_ {1} R \, \ zeta_ {l} ^ {\ prime} (k_ {1} R)} {\ zeta_ {l} (k_ {1} R)} \ simeq - \, л. $$ (32)

Таким образом, Q _ext имеет максимум

$$ \ Re [2 \, (1+ \ delta_ {1}) \, \ epsilon_ {1} + \ epsilon_ {2}] =0. $$ (33)

Полученное условие (33) учитывает возбуждение L режимы (термин δ ₁ ) и, следовательно, отличается от условия резонанса Фрелиха [17]:

$$ \ Re (2 \, \ epsilon_ {1} + \ epsilon_ {2}) =0. $$ (34)

В эксперименте [15] пиковые частоты ω _м и ширины резонанса Δ ω спектров экстинкции практически не зависят от 〈 D 〉. Эта особенность Δ ω кажется, не согласен с классической теорией Ми. Действительно, локальная теория предсказывает уширение плазмонных резонансов с уменьшением D (в A =0,25), как показано в таблице 1. В то же время нелокальная теория дает примерно одинаковую ширину резонанса, но разные положения пиков. Суперпозиция вкладов всех частиц дает значение Δ ω что замечательно согласуется с экспериментальными данными. Интересно, что нелокальная теория предсказывает уширение плазмонного резонанса пучка даже при A =0.

В ω > 4 эВ гладкие теоретические кривые на рис. 2 лежат выше мешанины узких близко расположенных экспериментальных пиков. В этом спектральном диапазоне преобладает межзонное поглощение, что подтверждается рис. 1. Наблюдаемые особенности спектра, вероятно, являются следствием перехода от непрерывных полос к дискретной структуре уровней. Такой квантово-размерный эффект был обнаружен ранее при исследовании оптических свойств золотых наносфер [19]. Когда размер серебряной сферы был увеличен до 〈 D 〉 =3.5 нм, поглощение сначала увеличивалось относительно максимума и образовывало плато с серией небольших эквидистантных провалов. Затем поглощение немного уменьшилось при 〈 D 〉 =4 нм.

Для изучения формирования синего крыла плазмонного резонанса мы рассчитали спектры экстинкции ультра-оловянных частиц серебра и представили их на рис. 3. Замечательной особенностью рис. 3 является полное исчезновение плазмонного резонанса при D =1 нм. Ранее этот эффект наблюдался при экспериментальном исследовании золотых наносфер [19]. В частности, на рис. 9 из [19] экспериментальные спектры частиц диаметром 1,7, 1,9, 2,0, 2,1, 2,3 и 2,5 нм сравнивались со спектрами, рассчитанными по локальной теории Ми. Согласие было плохим, не описывая уширение плазмонного резонанса и его положение [19]. Попытки улучшить подгонку путем изменения размера частиц и модификации диэлектрических функций не увенчались успехом. По мнению авторов [19], наблюдаемая аномально широкая или пониженная полоса коллективных колебаний не может быть приспособлена к предлагаемым поправкам локальной теории Ми. Как видно из рис. 4, ситуация кардинально меняется, если применить нелокальную теорию Ми. Обратите внимание, что мы не использовали никаких настраиваемых параметров. Таблица комплексного показателя преломления Джонсона и Кристи [20] была использована для определения диэлектрической функции золота. Другие параметры, включая A =1 и показатель преломления толуола (1,37) взяты из [19].

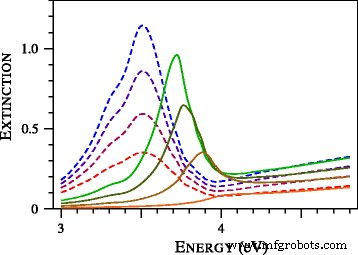
Нормированное сечение экстинкции частиц серебра диаметром 2,2, 1,8, 1,4 и 1,0 нм, рассчитанное с помощью локальных ( штриховых линий ) и нелокальный ( сплошные кривые ) Теории Ми. Чем меньше размер частицы, тем ниже кривая. Все теоретические сечения представлены в общепринятых относительных единицах

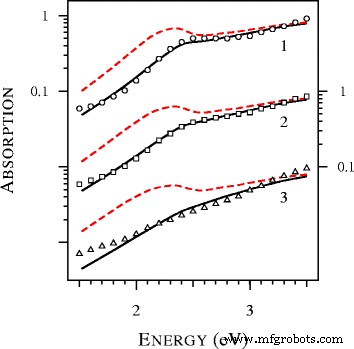
Спектры поглощения, рассчитанные по локальным ( пунктирным линиям ) и нелокальный ( сплошные линии ) Теория Ми и экспериментальные данные ( точки ) извлечено из рис. 9 из [19] для золотых сфер с D =2,5, 2,1 и 1,7 нм в толуоле (кривые 1 и кружки , кривые 2 и квадраты , а также кривые 3 и треугольники , соответственно). Все теоретические спектры нормированы на единицу при 4,12 эВ и смещены по вертикали

Волновые числа продольных волн

Продольные моды отличаются от поперечных гораздо более высокими значениями волновых чисел. Например, для расчетов, представленных на рис. 2, действительная часть \ (k_ {2} ^ {\ mathrm {L}} \) соответствует пространственному периоду \ (\ Lambda =2 \ pi / \ Re k_ { 2} ^ {\ mathrm {L}} \) уменьшается с 9 до 2 нм при ω возрастает с 3 до 4 эВ. В этом ω интервале абсолютное значение отношения \ (k_ {2} ^ {\ mathrm {L}} / k_ {2} \) уменьшилось со 130 до 100, а параметр δ уравнения (27) уменьшилось с 0,01 до 0,005 при θ ₁ = π / 4. Таким образом, можно сделать вывод, что возбуждением L-волн на плоской поверхности серебра можно пренебречь. Однако L Было обнаружено, что моды важны в кластерах серебра нанометрового размера.

Замена члена \ (- \, \ omega ^ {2} _ {\ mathrm {p}} / (\ omega ^ {2} + i \ Gamma \ omega) \) в уравнении. (16) автор: ε ^Т - ε _g согласно формуле. (21) позволяет переписать дисперсионное уравнение. (15) в следующем виде

$$ 1+ \ frac {3} {5} \, a ^ {2} + \ frac {3} {7} \, a ^ {4} + \ frac {3} {9} \, a ^ {6 } + \ dots =\ frac {1} {1- \ epsilon ^ {\ mathrm {T}} / \ epsilon _ {\ mathrm {g}}}. $$ (35)

В простейшем случае ε _g =1 и Γ =0, уравнение. (35) предсказывает, что металл прозрачен как для поперечной, так и для L-волны при ω > ω _p но оба k ^L и k ^Т сложны в ω < ω _p .

Если твердое тело прозрачно, продольная волна может быть возбуждена при наклонном падении p-поляризованной волны на плоскую поверхность. У этого эффекта есть несколько отличительных черт. Во-первых, продольные волны могут генерироваться на плоской поверхности, а для возбуждения поверхностных плазмон-поляритонов следует прилагать особые усилия [4, 5]. Во-вторых, в интерференционной картине интенсивность электромагнитного поля модулируется не вдоль, а перпендикулярно границе раздела. Следовательно, в плоскостях, параллельных поверхности, могут появиться пустоты из-за скалывания твердого тела. Согласно определению ω _p , условие ω > ω _p может встречаться в твердых телах (например, полупроводниках) с малой плотностью носителей тока. Мы не рассматриваем здесь этот случай, потому что формула ε ^L был получен для вырожденного электронного газа.