Теоретическое исследование двухосно-деформированных германиевых нанопроволок

Фон

Как элемент IV группы германий (Ge) имеет превосходство как в оптоэлектронике, так и в электронике и имеет отличную совместимость с кремниевой (Si) фотоникой. Существенной характеристикой Ge является то, что его прямая запрещенная зона составляет около 0,8 эВ (1,55 μ м) при 300 К. Подвижность как электрона, так и дырки в Ge намного выше, чем в Si. Таким образом, Ge был использован в высокоскоростных устройствах в современных интегральных схемах на основе Si [1, 2]. Что еще более интересно, Ge с деформацией растяжения предлагает оптимизацию в вышеупомянутых аспектах. Ge - непрямозонный полупроводник с небольшой разницей в 136 мэВ между L-долиной и Γ -долина [3]. Теоретически предсказано, что более ∼4,0% одноосной вдоль 〈111〉 [4] или ∼1,6–2,0% двуосной [5, 6] деформации растяжения может снизить Γ -долина ниже L-долины, тем самым превращая Ge в материал с прямой запрещенной зоной, что открывает новый путь излучения света из материалов группы IV. Другим важным моментом является то, что деформированный при растяжении Ge обеспечивает значительное увеличение подвижности носителей [7, 8] для реализации высокоскоростных дополнительных металлооксидных полупроводниковых устройств.

Нанопроволоки (ННК) демонстрируют привлекательные электронные и оптические свойства из-за большого отношения поверхности к объему и ограничения как носителей, так и фотонов в двух измерениях (2D) [9]. В последние годы Ge ННК (GeNW) на Si [10] или ННК Ge ​​/ Si ядро ​​/ оболочка [11] активно изучались из-за их потенциала в металлооксидных полупроводниковых полевых транзисторах (MOSFET) для Si микроэлектроники. И масштабируемая крутизна, и ток в прямом смысле были увеличены в три-четыре раза по сравнению с обычным Si p -MOSFET [12]. Таким образом, ожидалось, что эпитаксиальный рост боковых GeNW непосредственно на Si приведет к созданию высокопроизводительных полевых МОП-транзисторов. Zhang et al. обратился к тому, что сверхтонкие GeNW на Si (001) экспонируются с гранями {105} [13], которые имеют самую низкую предсказанную поверхностную энергию [14]. Кроме того, было показано, что напряженный Ge MOSFET на виртуальной подложке SiGe улучшает подвижность дырок [1]. Хотя боковые GeNW на Si с деформацией сжатия могут продемонстрировать значительное улучшение транспорта носителей, как предполагалось, они не могут быть преобразованы в прямую запрещенную зону. Для введения деформации растяжения в GeNW требуется сплав GeSn [15] и соединения III-Sb [16], которые имеют большую постоянную решетки, чем Ge. Несмотря на то, что для изготовления одноосно деформированных GeNW применялся механический метод [17, 18], сложность этого метода изготовления вряд ли может быть пригодна для монолитной интеграции в фотонику и электронику на основе Si. Кроме того, напряжение легко снимается в отдельно стоящих NW, тогда как боковые GeNW могут выдерживать очень высокие нагрузки сами по себе. Таким образом, для достижения прямого перехода запрещенной зоны, а также для увеличения подвижности носителей необходимы эпитаксиально выращенные латеральные GeNW с высокой двухосной деформацией растяжения.

На сегодняшний день бездислокационные и сильно деформированные при растяжении квантовые точки Ge на InP (001) продемонстрировали потенциал для прямого излучения из запрещенной зоны, смоделированный методом конечных элементов (МКЭ) [19]. Подобно этому, в этой работе мы теоретически предсказываем морфологию обнаженных поверхностей и направление роста двухосно-деформированных GeNW на релаксированном шаблоне GaSb, который можно выращивать непосредственно на Si с буферным слоем AlSb [16, 20]. Мы выбираем {110}, {105} и {111} в качестве открытых поверхностей боковых GeNW и сравниваем полное изменение энергии в установившейся системе. Мы игнорируем влияние дислокации и разрушения [21] в этой сильно деформированной системе для простоты. Моделирование на основе МКЭ показывает, что существует критическое количество Ge. Ниже критического значения GeNW проявляется с помощью {105}, а выше критического значения - с помощью {110}. Практически вся область GeNW может быть преобразована в прямую запрещенную зону, которая представляет собой разницу минимумов зоны проводимости и максимумов зоны легких дырок на Γ -точка. Кроме того, мы также качественно анализируем изменение эффективной массы носителей в зависимости от деформации на Γ - точка для косвенного предсказания увеличения подвижности электронов и дырок.

Методы

Боковые ННК обычно имеют треугольную форму поперечного сечения [22, 23]. Благодаря одномерному свойству NW, показанному на рис. 1a, модель конечной NW, подобная Zhang et al. в дополнительном материале к работе Ref. [13] можно правильно использовать для моделирования, в котором фиксируются как начальная, так и конечная поверхности, показанные на рис. 1b. Из-за граничного эффекта мы обсуждаем только центральную часть НП и считаем, что поперечное сечение этой части представляет ситуацию в бесконечно длинной НП. МКЭ используется для моделирования распределения деформации при растяжении в GeNW с несоответствием кристаллической решетки GaSb 7,7%. Мы рассчитываем приращение общей энергии системы после нанесения того же количества Ge в установившемся состоянии в трех ситуациях:(i) направление роста [100] с открытыми гранями {110} (ситуация A), (ii) направление роста [100], но с {105} обнаженных граней (ситуация B) и (iii) направление роста [110] с обнаженными гранями {111} (ситуация C). Поперечные сечения этих трех ситуаций показаны на рис. 1в. Площадь поперечного сечения остается неизменной, что соответствует равному количеству Ge.

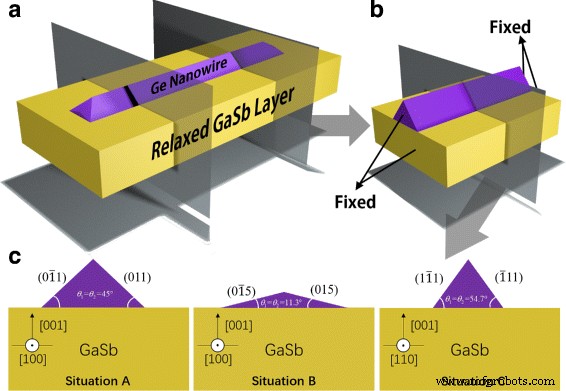
Схема GeNW на GaSb: а 3D-модель, b упрощенная конечная модель и c поперечные сечения GeNW с разными гранями

Общее изменение энергии системы на единицу длины (Дж / нм) включает общую разницу в энергии деформации, поверхностной энергии и краевой энергии [24] и может быть выражено как:

Первый член Δ E _{s т г а я нет} представляет собой разность энергии деформации стационарной системы до и после осаждения Ge и выражается в единице объема,

Результаты и обсуждения

Мы считаем, что система изначально находится в состоянии полной растягивающей деформации из-за большого несоответствия решеток (7,7%) между Ge и GaSb. На рисунке 2 показано двухмерное распределение остаточной деформации, включая деформацию в плоскости ε . _xx , деформация сдвига ε _xy , и вертикальная деформация ε _zz ситуации A с базовой шириной w =40 нм, например, в установившемся состоянии после релаксации. Определение деформации здесь ( a _Ges - а _Ge ) / а _Ge , где a _Ges и a _Ge - постоянные решетки напряженного и расслабленного Ge соответственно. Как видно на рис. 2а, ε _xx имеет максимальное значение около 15,4% на двух базальных краях, что намного больше, чем начальная деформация, но резко уменьшается от края к центру с минимальным значением около 3,3%. В z -направление снизу вверх GeNW, ε _xx также падает из-за релаксации GeNW. Распределение ε _zz имеет аналогичные характеристики с ε _xx на рис. 2б. В отличие от двухосной деформации в тонкой пленке Ge, рис. 2c показывает, что асимметрично распределенная компонента деформации сдвига GeNW играет важную роль в прямом запрещенном переходе. Распределение деформации в трех ситуациях довольно похоже. Тем не менее, значения компонентов деформации различаются в трех ситуациях из-за различного соотношения ширины и высоты ( W / H ), вызванное его формой. Ситуация B с GeNW, обнаженным {105} поверхностями, имеет наибольшее значение W / H 10, демонстрируя высокую деформацию, аналогичную таковой в тонкой пленке Ge. Ситуация C с открытыми поверхностями {111} также демонстрирует высокую деформацию, поскольку ориентация роста ННК вдоль [110] остается неизменным значением деформации, повышая значение ε _xx и ε _гг одновременно. Таким образом, деформация в плоскости практически не может быть ослаблена.

Распределение остаточной деформации GeNW в ситуации A с базовой шириной 40 нм: a деформация компонента x ε _xx , b деформация компонента z ε _zz , и c деформация сдвига в плоскости x-y ε _xy . Зигзагообразная форма внизу обозначает частичный слой подложки (следующее имеет то же значение)

В соответствии с распределением деформации можно получить приращение энергии деформации. Как обсуждалось ранее, ситуация B имеет наибольшее приращение энергии деформации, а ситуация A - наименьшее. Однако для изменения поверхностной энергии ситуация B дает убывающие отрицательные значения с увеличением площади поперечного сечения, а две другие ситуации показывают очень близкие положительные значения под той же площадью. Полный прирост энергии без учета краевого изменения энергии показан на рис. 3а. Результат показывает, что образование GeNW менее вероятно только в ситуации C из-за того, что приращение энергии никогда не бывает самым низким. Есть два различных последствия приращения энергии с увеличением площади, и вертикальная пунктирная линия отмечена, чтобы представить критическое значение площади, A _c =136,2 нм ² , что означает количество Ge. Если площадь меньше 136,2 нм ² , GeNW склонны формировать форму в ситуации B, но в ситуации A после внесения большего количества Ge. Результат расчета предсказывает, что деформированные при растяжении GeNW на GaSb могут предпочесть формирование высокой W / H треугольная форма в поперечном сечении, когда осаждается небольшое количество Ge, тогда как формируется низкий W / H один после превышения критического значения. На рис. 3b – e показаны распределения гидростатической деформации и суммы абсолютных значений компонент деформации сдвига в ситуации A и B под критической областью. Сравнивая ситуацию A с ситуацией B, несмотря на эту ситуацию, A имеет большее максимальное значение как гидростатической деформации, так и | ε _xy | + | ε _yz | + | ε _xz |, ситуация B имеет большую среднюю гидростатическую деформацию, но меньшее среднее значение | ε _xy | + | ε _yz | + | ε _xz |, Между тем, ситуация B демонстрирует небольшую разницу в пространственном распределении как гидростатической деформации, так и | ε _xy | + | ε _yz | + | ε _xz |, Эти свойства очень похожи на тонкую пленку Ge и объясняются ее высоким значением W . / H ценность. В результате, обращаясь к уравнениям. (5) и (6), ситуация B показывает меньшее значение Δ E _DT чем в ситуации A, что приводит к высокой вероятности превращения Ge в материал с прямой запрещенной зоной.

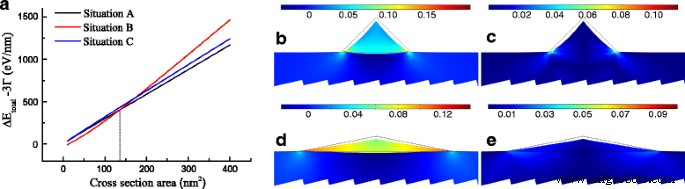
а Полное изменение энергии без учета краевого изменения энергии 3 Γ по сравнению с площадью поперечного сечения ( пунктирная линия - критическое значение минимумов около 136,2 нм ² в разных ситуациях). б - е гидростатическая деформация и | ε _xy | + | ε _yz | + | ε _xz | в б , c ситуация A и d , e ситуация B при критическом значении

Из-за высокой деформации при растяжении в GeNW почти вся область GeNW может быть преобразована в прямую запрещенную зону. На рисунке 4а показано распределение Δ E _DT с увеличением размера GeNW. Значение Δ E _DT падает сверху вниз в GeNW. Интересно, что минимум Δ E _DT расположен на нижнем краю поперечного сечения в ситуации B, но в центре внизу в ситуации A. Причина этого другого распределения заключается в том, что значительная деформация сдвига на нижнем крае в ситуации A больше способствует \ (\ Delta E_ {c} ^ {\ mathrm {L}} \), чем в ситуации B. Для GeNW в ситуации B ниже критической области среднее значение Δ E _DT намного ниже, чем в ситуации A выше критической области, как показано на рис. 4b. В критической точке среднее значение Δ E _DT внезапно возрастает со значения -0,308 до -0,137 эВ. Кроме того, для той же формы распределение и среднее значение Δ E _DT в основном похожи, без явного отношения к размеру. Чтобы обнаружить внутреннюю связь с деформацией в GeNW, мы построим гидростатическую составляющую деформации в основании GeNW с базисной шириной на рис. 5. Кривые гидростатической составляющей деформации с различными размерами в зависимости от относительного положения основания в GeNW почти перекрываются, за исключением разницы в периферической области. Последовательные последствия находятся в ε _xx и сумма составляющих абсолютного сдвига. Таким образом, вызванное деформацией значение Δ E _DT имеет идентичное распределение в GeNW с той же формой.

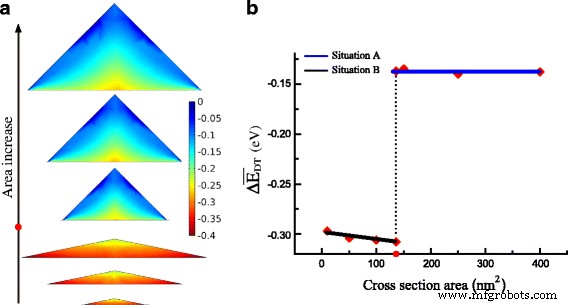
а Распределение Δ E _DT с увеличением площади ( цветная полоса обозначает значение Δ E _DT ). б Среднее значение Δ E _DT по сравнению с площадью. Критическое значение отмечено красной точкой . по оси площади

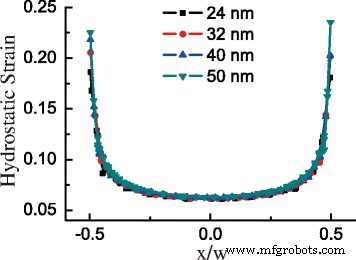
Компонент гидростатической деформации у основания GeNW в зависимости от x / w с разной базальной шириной

Далее, мы моделируем карту запрещенной зоны, вызванную деформацией, в поперечном сечении GeNW шириной 40 нм, показанном на рис. 6а. Пространственное распределение ширины запрещенной зоны получается из переменной величины зависящих от деформации краев полосы на Γ -точка. На рисунке 6b показана энергия края зоны при Γ -точка вдоль z -направление GeNW. Мы обнаружили, что и зона проводимости, и края валентной зоны, включая зону легких дырок и зону тяжелых дырок, значительно изменяются в первые 15 нм, а затем незначительно. Верхние части полосы легких и тяжелых дырок разделяются и имеют тенденцию смещаться в противоположных направлениях с увеличением деформации растяжения. Как видно из рис. 6a, b, ширина запрещенной зоны значительно увеличивается на первых 15 нм и достигает примерно 0,30 эВ, а затем слегка изменяется около значения 0,24 эВ, которое является шириной запрещенной зоны в большинстве областей GeNW. Поскольку максимумы полосы легких дырок выше, чем максимумы полосы тяжелых дырок на Γ -точка в GeNW дырки в валентной зоне предпочитают располагаться в максимумах зоны легких дырок. Таким образом, электронно-дырочная рекомбинация будет происходить между минимумом зоны проводимости и максимумом зоны легких дырок на Γ - точка, если пренебречь перекрытием пространственно-зависимых волновых функций электрона и дырки. Интересно, что максимумы зоны легких дырок перемещаются даже выше минимумов зоны проводимости в области дна ННК, отмеченной черной кривой на рис. 6а, с гидростатической деформацией более ∼5.0%. Отрицательная запрещенная зона, которую мы рассчитываем при высокой деформации растяжения, может вызвать сложные последствия, такие как полуметаллическая [31] или перевернутая [32] зонная структура.

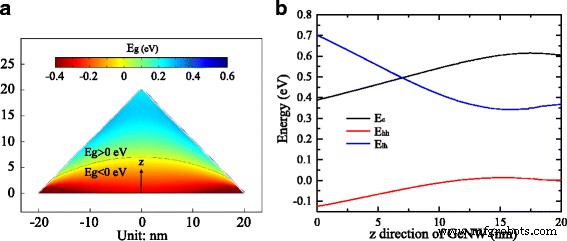
а Зависимая от деформации запрещенная зона в GeNW, распределенная по позициям. б Энергии края зоны, зависящие от деформации вдоль z направление в GeNW

Наконец, подвижность электронов и дырок будет увеличиваться при такой высокой деформации растяжения в GeNW. Для релаксированного Ge в электронный транспорт в основном вносят вклад электроны, находящиеся в L-долине. Когда Ge находится под действием растягивающей деформации, поэтому Γ -долина находится ниже L-долины, как показано на рис. 3а, основной вклад в перенос электронов вносит Γ -Долина. С другой стороны, преобладающее участие дырок в переносе происходит из зоны легких дырок на Γ -точка при сильной деформации растяжения, а зона тяжелых дырок занимает максимумы валентной зоны в релаксированном случае. Из-за гораздо меньшей эффективной массы электрона на Γ -точка, чем в L-точке, а также уменьшенная эффективная масса от максимумов зон тяжелых дырок до максимумов зон легких дырок, подвижность не только электронов, но и дырок может быть увеличена. Теоретически можно предсказать, что деформация растяжения уменьшит эффективную массу электронов и дырок на Γ -точка в модели квантовой точки от Califano и Харрисон [29]. Хотя метод количественного расчета не подходит для нашей модели NW, мы качественно предполагаем, что деформация растяжения может изменять эффективную массу при k =0 за счет увеличения кривизны дисперсионного соотношения для малых k в непосредственной близости от Γ -точка. Таким образом, подвижность как электронов, так и дырок может быть увеличена в деформированных растяжением GeNW. Расщепляющиеся валентные зоны также вызывают сильную электрон-фононную связь и внутризонное рассеяние [33], что ограничивает подвижность дырок ниже подвижности электронов.

Выводы

Таким образом, мы предложили деформированные при растяжении GeNW на GaSb, сравнивая три различных ситуации через изменение полной энергии до и после осаждения Ge. Результат показывает, что GeNW имеет тенденцию формировать поверхности {105} вдоль направления роста 〈100〉 до критического количества, в то время как подвергается воздействию поверхностей {110} после критического количества. Поле остаточной деформации и анализ запрещенной зоны показали, что одна и та же форма имеет одинаковое распределение как по деформации, так и по Δ E _DT независимо от размера. Кроме того, деформация в плоскости и гидростатическая деформация уменьшаются не только от краев к центру, но и снизу вверх во всех ситуациях. Из-за высокой деформации растяжения почти весь GeNW на GaSb может быть преобразован в материал с прямой запрещенной зоной в двух возможных ситуациях. Кроме того, легкие дырки в основном участвуют в электронно-дырочной рекомбинации и переносе электрического тока на Γ -точка, потому что максимумы зоны легких дырок становятся максимумами валентной зоны при высокой деформации растяжения. Подвижность не только электронов, но и дырок может быть увеличена за счет уменьшения эффективной массы носителей заряда на Γ -точка определяется деформацией растяжения. Теоретически предсказанные привлекательные характеристики подразумевают, что деформированные при растяжении GeNW перспективны для применения в оптоэлектронике для источников света и микроэлектронике для высокоскоростных устройств в Si-фотонике и электронике соответственно.