Эффекты взаимодействия в сборке магнитных наночастиц

Фон

Магнитная гипертермия [1,2,3,4] - одно из наиболее перспективных направлений современных биомедицинских исследований, связанных с лечением рака. На способность магнитных наночастиц генерировать тепло в переменном внешнем магнитном поле влияют различные факторы, такие как их геометрические и материальные параметры, концентрация наночастиц в среде, а также частота и амплитуда переменного магнитного поля. В данной работе теоретически исследуется влияние взаимного магнитодипольного взаимодействия на удельную скорость поглощения (SAR) ансамбля магнитных наночастиц в переменном магнитном поле. Наночастицы оксидов железа кажутся наиболее перспективными для использования в магнитной гипертермии [2,3,4,5], поскольку они биосовместимы и биоразлагаемы и могут быть обнаружены в организме человека с помощью клинической МРТ. В данной работе мы рассматриваем ансамбли наночастиц с магнитными параметрами, типичными для наночастиц оксида железа. Недавно было обнаружено [4, 6], что, будучи внедренными в биологическую среду, например, в опухоль, магнитные наночастицы оказываются прочно связанными с окружающими тканями. Следовательно, вращение магнитных наночастиц как целого под действием переменного внешнего магнитного поля сильно затруднено. В таком случае броуновская релаксация несущественна [4]. Следовательно, необходимо учитывать только движение магнитных моментов частицы под действием переменного магнитного поля и тепловых флуктуаций. Кроме того, необходимо учитывать влияние магнитно-дипольного взаимодействия между частицами. Последний эффект особенно важен, поскольку магнитные наночастицы в биологических средах имеют тенденцию к агломерации [2, 4, 7], образуя плотные агрегаты наночастиц, имеющих фрактальную [8, 9] геометрическую структуру.

Влияние тепловых флуктуаций на рассеяние тепла в разреженной ансамбле магнитных наночастиц в переменном магнитном поле подробно изучено в работах [8,11]. [10,11,12,13]. В частности, было показано [10], что SAR такой сборки существенно зависит от среднего диаметра наночастиц, среди других факторов. Для разреженной сборки наночастиц детальные расчеты [10] позволяют определить оптимальный диаметр наночастиц при заданных магнитных параметрах частицы и заданной амплитуде и частоте переменного магнитного поля. При оптимальном выборе геометрических и магнитных параметров наночастиц прогнозируются очень высокие значения SAR, порядка 1000 кВт / кг [10, 11]. Примечательно, что значения SAR, полученные в ряде экспериментов [14,15,16,17], действительно близки к приведенным выше теоретическим оценкам. В то же время во многих экспериментах [5, 18,19,20,21] были измерены значительно более низкие значения SAR ~ 20–50 кВт / кг. Этот факт, скорее всего, можно объяснить влиянием сильного магнитодипольного взаимодействия в плотных ансамблях магнитных наночастиц.

Действительно, экспериментально показано [22, 23], что SAR в плотной сборке магнитных наночастиц существенно зависит от соотношения сторон исследуемого образца, то есть отношения длины образца к ширине. Это косвенное свидетельство влияния магнитодипольного взаимодействия на отклик ансамбля наночастиц на переменное внешнее магнитное поле. Влияние магнитодипольного взаимодействия на скорость поглощения энергии сборкой магнитных наночастиц изучалось в ряде недавних теоретических и экспериментальных исследований [7, 24, 25, 26, 27, 28, 29, 30, 31, 32. , 33,34,35,36,37,38]. Однако необходимы дальнейшие исследования, чтобы учесть фрактальную природу [8, 9] распределения наночастиц в биологических средах.

Чтобы четко увидеть эффект магнитодипольного взаимодействия, в этой статье мы сначала рассчитываем SAR совокупности невзаимодействующих наночастиц оксида железа. Для изучения влияния магнитодипольного взаимодействия численно решается стохастическое уравнение Ландау – Лифшица [13, 39,40,41], которое одновременно учитывает как наличие тепловых флуктуаций магнитных моментов частиц, так и магнитодипольное взаимодействие. между наночастицами кластеров. Рассмотрены два типа магнитных кластеров:обычные случайные трехмерные кластеры наночастиц, распределенных в жесткой среде, и фрактальные кластеры наночастиц, которые обычно возникают во внутриклеточном пространстве. Обратите внимание, что внутри кластера наночастицы связаны сильным магнитодипольным взаимодействием. В то же время для разреженной сборки кластеров магнитным взаимодействием между кластерами в первом приближении можно пренебречь.

Показано, что влияние магнитодипольного взаимодействия на свойства разреженной сборки случайных трехмерных кластеров определяется в основном плотностью упаковки наночастиц η = N _p V / V _cl , где N _p - среднее количество частиц в кластере, V - объем наночастицы, а V _cl - объем кластера. Было обнаружено, что площадь петли гистерезиса и SAR сборки значительно уменьшается, когда плотность упаковки трехмерных кластеров увеличивается в диапазоне исследованных плотностей упаковки, 0,005 ≤ η <0,4. Для фрактальных кластеров магнитных наночастиц, помимо значительного снижения SAR, максимальная скорость поглощения, как правило, смещается в сторону меньших диаметров частиц. Обнаружено также, что SAR фрактальных кластеров заметно возрастает с увеличением толщины немагнитных оболочек на поверхности наночастиц. Этот эффект может быть важен для применения сборок магнитных наночастиц в магнитной гипертермии.

Численное моделирование

Невзаимодействующие наночастицы

Поучительно сначала напомнить о поведении ансамбля невзаимодействующих суперпарамагнитных наночастиц в переменном магнитном поле. Это позволяет отчетливо увидеть влияние магнитодипольного взаимодействия на свойства сборки. На основе уравнения Фоккера – Планка, выведенного W.F. Браун [39], можно получить приближенное кинетическое уравнение [10] для численности населения n ₁ ( т ) и n ₂ ( т ) двух потенциальных ям одноосной суперпарамагнитной наночастицы

Здесь τ ₁ ( Т ) и τ ₂ ( Т ) - соответствующие времена релаксации при заданной температуре T для первой и второй потенциальных ям соответственно. Времена релаксации τ ₁ ( Т ) и τ ₂ ( Т ) существенно зависят от амплитуды и направления приложенного магнитного поля относительно оси легкой анизотропии частицы (см. приложение в [10]). Итерационную процедуру можно использовать для расчета количества заселенных скважин n ₁ ( т ) и n ₂ ( т ) для нескольких периодов переменного магнитного поля. Достаточно получить стационарную петлю гистерезиса частицы в переменном магнитном поле. Для этого можно использовать приближенное соотношение для составляющей приведенной намагниченности частицы вдоль направления магнитного поля

Здесь θ ₀ - угол внешнего магнитного поля относительно оси легкой анизотропии частицы, θ _{мин, 1} и θ _{мин, 2} - положения минимумов потенциальной ямы как функции приведенного приложенного магнитного поля, h _e ( т ) = H ₀ грех ( ωt ) / H _а , где ω =2π f угловая частота, H _а - поле анизотропии частицы. Чтобы получить петлю гистерезиса сборки случайно ориентированных независимых наночастиц, необходимо усреднить приведенную намагниченность m _h ( т ) по направлениям магнитного поля. Стоит отметить, что точность приближенного аналитического решения уравнения. (1), (2) уравнения Фоккера-Планка были подтверждены [10] путем прямого сравнения с численными решениями стохастического уравнения Ландау-Лифшица для невзаимодействующих магнитных наночастиц.

Кластеры наночастиц

Чтобы исследовать влияние магнитодипольного взаимодействия на удельную скорость поглощения ансамбля взаимодействующих магнитных наночастиц в переменном магнитном поле, в данной статье мы изучаем поведение разбавленного ансамбля обычных 3D-кластеров суперпарамагнитных наночастиц и фрактальных наночастиц. кластеры [8, 9], которые обычно возникают в биологических средах, загруженных мелкими магнитными наночастицами.

Квазисферический трехмерный кластер наночастиц, схематически показанный на рис. 1а, может быть охарактеризован его радиусом R _cl , и количество наночастиц, N _p >> 1, в пределах своего объема. Предполагается, что наночастицы имеют примерно одинаковый диаметр D , и их центры, { r _я }, я =1, 2, .. N _p , случайным образом распределяются в объеме кластера. Мы также предполагаем, что частицы покрыты тонкими немагнитными оболочками, так что обменное взаимодействие между соседними наночастицами кластера отсутствует. Как мы упоминали выше, такой 3D-кластер характеризуется плотностью упаковки наночастиц η = N _p V / V _cl . Это общий объем магнитного материала, распределенный в объеме кластера. Среднее расстояние между наночастицами кластера можно определить с помощью соотношения D _av =(6 V _cl / πN _p ) ^1/3 . Тогда плотность упаковки наночастиц определяется как η =( D / D _av ) ³ .

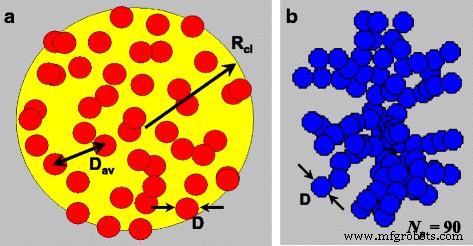
Геометрия квазисферического случайного трехмерного кластера однодоменных наночастиц ( a ) и фрактальный кластер ( b ) с фрактальными дескрипторами D _f =2.1 и k _f =1,3

Для сборки полностью случайных трехмерных кластеров ориентации осей легкой анизотропии наночастиц { e _я }, я =1, 2, .. N _p , выбираются случайно и независимо на единичной сфере. В качестве альтернативы можно предположить, что при образовании кластеров в растворе под действием магнитостатического взаимодействия возникает определенная корреляция в распределении направлений осей легкой анизотропии наночастиц. Одна из возможностей описания таких частично упорядоченных кластеров состоит в предположении, что оси легкой анизотропии наночастиц равномерно распределены в телесном угле θ < θ _макс , в сферических координатах.

Случайные 3D-кластеры с заданным количеством частиц N _p диаметром D были созданы в этом исследовании следующим образом. Во-первых, мы сгенерировали достаточно плотный и приблизительно равномерный набор N случайные точки { ρ _я } в сферическом объеме радиуса R _cl , так что | ρ _я | ≤ R _cl для всех сгенерированных точек i =1, 2 ... N , N >> N _p . Центр первой наночастицы был помещен в первую случайную точку r ₁ = ρ ₁ . Тогда все случайные точки с координатами | ρ _я - г ₁ | ≤ D были удалены из первоначального набора случайных точек. После этой операции любую точку из оставшегося набора случайных точек можно было бы использовать в качестве центра второй наночастицы. Например, можно просто указать r ₂ = ρ ₂ . На следующем шаге удаляются все случайные точки, координаты которых удовлетворяют неравенству | ρ _я - г ₂ | ≤ D . Эта процедура повторяется до тех пор, пока все N _p центры наночастиц размещаются в объеме кластера. В результате все случайные центры наночастиц лежат внутри сферы радиусом R _cl , так что | r _я | ≤ R _cl , я =1, 2, ... N _p . Кроме того, ни одна из наночастиц не находится в прямом контакте с соседними наночастицами. Этот алгоритм позволяет строить случайные квазисферические трехмерные кластеры магнитных наночастиц для умеренных значений объемной доли наночастиц η <0,5.

Для заданного набора начальных параметров, т. Е. D , R _cl , и N _p , различные случайные трехмерные кластеры различаются наборами координат центров наночастиц { r _я } и ориентации { e _я } осей легкой анизотропии частицы. Однако расчеты показывают, что в пределе N _p >> 1, петли гистерезиса, полученные для различных реализаций случайных величин { r _я } и { e _я } мало отличаются друг от друга. Чтобы охарактеризовать поведение разбавленной сборки случайных кластеров наночастиц, необходимо вычислить петлю гистерезиса сборки, усредненную по достаточно большому количеству случайных реализаций кластеров. Обнаружено, что в пределе N _p >> 1, усредненная петля гистерезиса сборки кластеров имеет довольно небольшую дисперсию даже при усреднении по 20–30 независимым реализациям случайных кластеров с фиксированными значениями начальных параметров D , R _cl , и N _p .

Геометрия фрактальных кластеров однодоменных наночастиц характеризуется [42, 43] фрактальными дескрипторами D _f и k _f . По определению общее количество наночастиц N _p во фрактальном кластере задается соотношением \ ({N} _p ={k} _f {\ left (2 {R} _g / D \ right)} ^ {D_f} \), где D _f - фрактальная размерность, k _f - фрактальный префактор, а R _г радиус вращения. Он определяется [43] через средний квадрат расстояний между центрами частиц и геометрическим центром масс агрегата. В этой статье фрактальные кластеры с различными фрактальными дескрипторами были созданы с использованием известного алгоритма Филиппова и др. [43]. В качестве примера на рис. 1б показана геометрическая структура фрактального кластера с фрактальными дескрипторами D . _f =2.1 и k _f =1.3, состоящий из N _p =90 однодоменных наночастиц. С геометрической точки зрения кажется, что основное различие между трехмерными и фрактальными кластерами состоит в том, что в последнем случае каждая наночастица имеет по крайней мере одного соседа, расположенного на максимально близком расстоянии между центрами наночастиц, равном диаметру наночастицы D .

Динамика единичного вектора намагниченности \ ({\ overrightarrow {\ alpha}} _ i \) i -я однодоменная наночастица кластера определяется стохастическим уравнением Ландау – Лифшица (ЛЛ)

где γ гиромагнитное отношение, κ - феноменологический параметр затухания, γ ₁ = γ / (1+ κ ² ), \ ({\ overrightarrow {H}} _ {ef, i} \) - эффективное магнитное поле, а \ ({\ overrightarrow {H}} _ {th, i} \) - тепловое поле. Эффективное магнитное поле, действующее на отдельную наночастицу, можно рассчитать как производную от полной энергии кластера

Полная магнитная энергия кластера W = Вт _а + W _Z + W _м представляет собой сумму энергии магнитокристаллической анизотропии W _а , Энергия Зеемана Вт _Z частиц в приложенном магнитном поле \ ({\ overrightarrow {H}} _ 0 \ sin \ left (\ omega t \ right) \), а энергия взаимного магнитодипольного взаимодействия частиц W _м .

Для наночастиц почти сферической формы с одноосным типом магнитной анизотропии энергия магнитокристаллической анизотропии определяется как

где e _я - ориентация оси легкой анизотропии i -я частица кластера. Энергия Зеемана Вт _Z кластера в приложенном магнитном поле определяется как

Далее, для сферических однородно намагниченных наночастиц магнитостатическая энергия кластера может быть представлена ​​как энергия взаимодействующих точечных диполей, расположенных в центрах частиц r _я внутри кластера. Тогда энергия магнитодипольного взаимодействия

где n _ij - единичный вектор вдоль линии, соединяющей центры i -th и j -ые частицы соответственно.

Таким образом, эффективное магнитное поле, действующее на i -я наночастица кластера имеет вид

где H _а =2 К / M _s. - поле анизотропии частицы.

Тепловые поля, \ ({\ overrightarrow {H}} _ {th, i} \), i =1, 2 ... N _p , действующие на различные наночастицы кластера, статистически независимы, со следующими статистическими свойствами [39] их компонентов для каждой наночастицы

Здесь k _B постоянная Больцмана, δ _αβ - символ Кронекера, а δ ( т ) - дельта-функция.

Процедура решения стохастических дифференциальных уравнений. (3), (8) и (9) подробно описаны в статьях. [13, 40, 41].

Результаты и обсуждение

Невзаимодействующие наночастицы оксида железа

Рассмотрим разбавленную сборку суперпарамагнитных наночастиц со средним диаметром D . Предполагается, что частицы плотно упакованы в окружающей среде, а их оси легкой анизотропии ориентированы в пространстве случайным образом. Петля гистерезиса такой сборки в переменном магнитном поле H = H ₀ грех ( ωt ) можно рассчитать [10] с помощью формул. (1) и (2). Такой подход в силу своей простоты позволяет проводить детальные расчеты петель гистерезиса сборки для различных размеров частиц в зависимости от частоты и амплитуды переменного магнитного поля. В проведенных расчетах в соответствии с экспериментальными данными [2,3,4,5,6] намагниченность насыщения наночастиц оксида железа принята равной M _s. =70 часов утра ² / кг, постоянная магнитной анизотропии K =10 ⁴ Дж / м ³ . Температура сборки T =300 K, а диаметры наночастиц находятся в диапазоне D =10–30 нм. Эти параметры кажутся типичными для экспериментов, проводимых с наночастицами оксида железа.

На рисунке 2 показан SAR невзаимодействующих ансамблей наночастиц оксида железа на различных частотах при фиксированной амплитуде переменного магнитного поля H ₀ =8 кА / м. Как видно, для диапазона частот, характерных для магнитной гипертермии, f =200–500 кГц, SAR имеет максимум для сборки наночастиц оксида железа диаметром D =20–21 нм. Примечательно, что даже при относительно умеренной амплитуде переменного магнитного поля SAR сборки достигает достаточно высоких значений, 350–450 кВт / кг, при правильном выборе диаметров наночастиц.

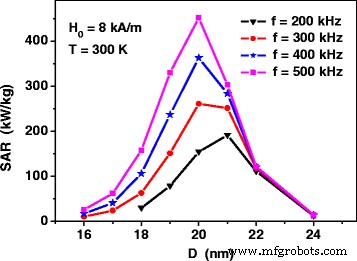
Удельная скорость поглощения невзаимодействующей сборки наночастиц оксидов железа, полученная с помощью формул. (1) и (2) как функция среднего диаметра частиц при различных частотах переменного магнитного поля

Однако экспериментально измеренные значения SAR для ансамблей наночастиц оксидов железа, как правило, значительно ниже [18,19,20,21] этих теоретических значений. Как мы увидим в следующем разделе, этот факт можно объяснить [22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38] с помощью влияние сильного магнитодипольного взаимодействия в плотных ансамблях магнитных наночастиц.

Сборка трехмерных кластеров

Теперь рассмотрим петли гистерезиса разреженной сборки трехмерных случайных кластеров, имеющих простые оси анизотропии отдельных наночастиц, случайно ориентированных в пространстве. Как показано на рис. 2, для сборки невзаимодействующих наночастиц оксида железа пик поглощения энергии в переменном магнитном поле соответствует частицам диаметром D =20 нм. Поэтому сначала мы рассчитали петли гистерезиса сборки трехмерных кластеров с диаметром частиц D =20 нм.

На рис. 3а показана эволюция петель гистерезиса сборки в зависимости от среднего расстояния между центрами наночастиц D . _av при фиксированном значении диаметра частицы D . Частота и амплитуда переменного магнитного поля фиксированы на f . =400 кГц и H ₀ =8 кА / м соответственно. Количество частиц в кластерах равно N . _p =40. Расчеты проводятся при T =300 К, а постоянная магнитного затухания принята равной κ =0,5.

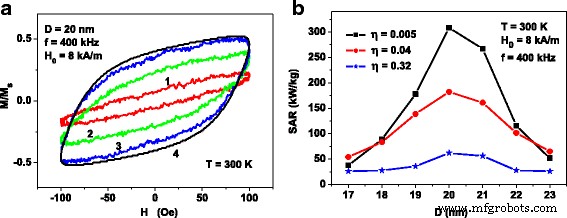
( а ) Эволюция петель гистерезиса разбавленной сборки кластеров наночастиц оксида железа диаметром D =20 нм для различных соотношений D _av / D :( 1 ) D _av / D =1,46; ( 2 ) D _av / D =2,92; ( 3 ) D _av / D =5,84. Петля гистерезиса 4 соответствует сборке невзаимодействующих наночастиц одного диаметра. Он рассчитывается с помощью формул. (1) и (2). ( б ) SAR как функция среднего диаметра наночастиц D для разбавленных сборок кластеров наночастиц с различной плотностью упаковки η

Очевидно, что уменьшение среднего расстояния между наночастицами кластера приводит к увеличению интенсивности магнитодипольного взаимодействия внутри кластера. Обратите внимание, что для N _p =40, отношения D _av / D указанные на рис. 3а соответствуют плотностям упаковки кластеров η =0,005, 0,04 и 0,32 соответственно. На рис. 3а видно, что площадь петли гистерезиса быстро уменьшается в зависимости от параметра η . Для сравнения на рис. 3а также показана петля гистерезиса 4, рассчитанная для сборки невзаимодействующих частиц, т.е. в пределе D _av / D → ∞, N _p =Const, используя уравнения (1) и (2).

Видно, что петля гистерезиса 3 ( η =0.005) на рис. 3а оказывается близким к петле гистерезиса сборки невзаимодействующих наночастиц. Следовательно, в случае η ≤ 0,005 магнитодипольным взаимодействием наночастиц внутри кластера можно пренебречь. Однако для η ≥ 0,04 магнитодипольное взаимодействие оказывает существенное влияние на свойства сборки случайных трехмерных кластеров. Аналогичная эволюция петель гистерезиса сборки была получена и для частот f =300 и 500 кГц соответственно.

Петли гистерезиса, показанные на рис. 3а, рассчитаны для различных соотношений D _av / D , но для фиксированного количества наночастиц в кластере N _p =40. Однако детальное компьютерное моделирование показывает, что форма петли гистерезиса разбавленной сборки случайных трехмерных кластеров практически не меняется, если количество частиц N _p >> 1, а радиус кластера R _cl изменяются так, чтобы плотность упаковки наночастиц η остается постоянным. Следовательно, петля гистерезиса разбавленной сборки случайных трехмерных кластеров зависит в основном от плотности упаковки кластеров η .

На рисунке 3b показаны SAR сборок случайных кластеров наночастиц оксида железа для различных η ценности. SAR сборки рассчитывается [10] как SAR = M _s fA / ρ , где A - площадь петли гистерезиса в переменных ( M / M _s. , H ), ρ плотность наночастиц оксида железа, которая предполагается равной ρ =5 × 10 ³ кг / м ³ . Как показано на рис. 3b, SAR уменьшается в зависимости от η за счет увеличения интенсивности магнитодипольного взаимодействия внутри кластеров. При этом зависимость SAR сборки от среднего диаметра частиц сохраняется, но становится менее выраженной.

Для малых значений η ≤ 0,005, SAR случайной сборки трехмерных кластеров фактически совпадает с SAR для сборки невзаимодействующих наночастиц, показанной на рис. 2. С другой стороны, SAR падает примерно в шесть раз, когда плотность упаковки кластеров увеличивается до <я> η =0,32. Затем оно приближается к типичным значениям SAR ~ 50–100 кВт / кг, которые были получены в ряде экспериментов [5, 18,19,20,21] со сборками наночастиц оксида железа.

Сборка фрактальных кластеров

Аналогичные расчеты были проведены для разреженных ансамблей фрактальных кластеров наночастиц с различными фрактальными дескрипторами. Как показано на рис. 4, для фрактальных кластеров наночастиц SAR как функция диаметра частицы также значительно уменьшается по сравнению со сборкой невзаимодействующих наночастиц. Однако, в отличие от сборки трехмерных кластеров, пиковые значения SAR систематически смещаются в сторону меньших диаметров частиц, за исключением случая фрактальной размерности D _f =2.7, что близко к случаю трехмерных кластеров с D _f =3,0. Интересно также отметить, что для неоптимальных диаметров наночастиц, например, для наночастиц с диаметром D ≤ 17 нм, влияние магнитодипольного взаимодействия приводит к увеличению SAR по сравнению со случаем сборки невзаимодействующих наночастиц, так как SAR сборки невзаимодействующих наночастиц очень мала для наночастиц с диаметром Д ≤ 17 нм.

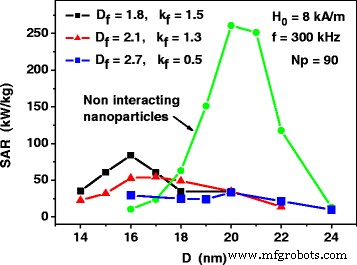
SAR как функция среднего диаметра наночастиц D для разреженных ансамблей фрактальных кластеров наночастиц с различными фрактальными дескрипторами. SAR сборки невзаимодействующих наночастиц рассчитывается с помощью формул. (1) и (2)

Расчеты, представленные на рис. 4, проводились в предположении существования тонких немагнитных оболочек толщиной t _Ш =1 нм на поверхности магнитных наночастиц. This prevents the nanoparticles of the fractal cluster from direct exchange interaction. Evidently, the increase of the non-magnetic shell thickness reduces the intensity of the magneto- dipole interaction of closest nanoparticles, as the average distance between the magnetic cores on the nanoparticles increases. Figure 5 shows that the increase of the non-magnetic shell thickness is a proper way to raise the SAR of the assembly of fractal clusters of nanoparticles. Namely, for sufficiently large thickness of non-magnetic shells the dependence of the SAR on the particle diameter resembles that for weakly interacting magnetic nanoparticles. This fact may be important for the application of magnetic nanoparticle assemblies in magnetic hyperthermia.

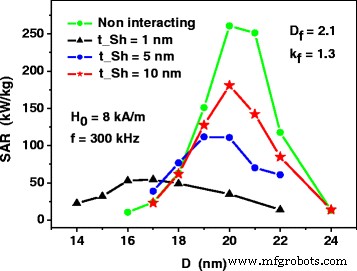
The dependence of the SAR of dilute assembly of fractal clusters on the thickness t _Sh of the non-magnetic shells at the surface of the nanoparticles. The SAR of the assembly of non-interacting nanoparticles is calculated by means of Eqs. (1) and (2)

Выводы

The main conclusion of this study is that the SAR of a dilute assembly of clusters of magnetic nanoparticles in alternating magnetic field is significantly reduced with increasing of the intensity of magneto-dipole interaction in the clusters. For usual 3D clusters of nanoparticles, the intensity of the magneto-dipole interaction can be characterized by dimensionless packing density, η  = N _p V /V _cl  = (D /D _av ) ³ . The latter determines the average distance between the nanoparticles of the cluster. The calculations show that for the assembly of random 3D clusters, the energy absorption peak, which for iron oxide nanoparticles corresponds to particles with average diameter D  = 20 nm, is reduced about six times when the packing density increases from η  = 0.005 up to η  = 0.32. The dependence of the assembly SAR on the mean nanoparticle diameter is retained with increase of η , but becomes less pronounced.

For dilute assemblies of fractal clusters of magnetic nanoparticles, the SAR values also decrease several times irrespective on the fractal descriptors of the assembly. In addition, the peak values of SAR are shifted systematically to smaller particle diameters, as a rule. It is important to note, however, that the increase of the non-magnetic shell thickness at the nanoparticle surfaces restores the SAR values close to that of the assembly of weakly interacting nanoparticles. This fact can be important for various biomedical applications of magnetic nanoparticle assemblies.

The model considered in this paper takes into account the geometrical structure of nanoparticle assemblies observed experimentally in biological media [4, 8, 9] (in particular in tumors), i.e., the agglomeration of nanoparticles in a sufficiently dense fractal clusters of different sizes, with different numbers of nanoparticles in the clusters. The stochastic LL Eq. (3) accurately describes the real dynamics of the magnetic moments of nanoparticles taking into account both the magneto-dipole interaction between the particles and the effect of thermal fluctuations. The cluster model studied allows obvious generalization that can make it more practical. First, it is necessary to take into account the size distribution of magnetic nanoparticles in the assembly. Second, in some cases exchange interaction may exist between neighboring nanoparticles of the cluster if they are in direct atomic contact.

The theoretical results obtained in this study seem to be in a satisfactory agreement with recent experimental data [35] for iron oxide nanoparticles of optimal diameters. Indeed, according to Ref. [35], the SAR of the iron oxide nanoparticles increases with the average diameter of the nanoparticles and peaks for nanoparticles with mean diameter D  = 20–21 nm. In addition, the SAR decreases [35] with a decrease in the average distance between the nanoparticles due to increasing intensity of the magneto-dipole interaction.

Unfortunately, in some experimental studies [5, 21] carried out to optimize the properties of magnetic nanoparticles for use in magnetic hyperthermia, often do not take into account the theoretical predictions [10, 11] about significant dependence of the assembly SAR on the characteristic size of the magnetic nanoparticles. As shown in this paper, this dependence can be substantial even for rather dense nanoparticle assemblies. From a theoretical point of view, it is obvious [10] that the assembly of iron oxide nanoparticles with very small, D  ≤ 10 nm, or too big, D  ≥ 30 nm diameters can hardly provide a sufficiently high SAR values for typical for magnetic hyperthermia frequencies, f  = 200–600 kHz, and magnetic field amplitudes H ₀  ~ 8 kA/m. The creation of mono-crystalline iron oxide nanoparticles with sharp size distribution near the optimal diameter has to be promising for application in magnetic hyperthermia.