Перколяционный магнетизм в сегнетоэлектрических наночастицах

Фон

Изготовление и интенсивные исследования наночастиц из диэлектрических оксидов, немагнитных в объеме, выявили в них ферромагнетизм, например, в HfO ₂ [1], TiO ₂ [2,3,4], ZnO [5,6,7], SnO ₂ [7, 8], КТаО ₃ [9], и KNbO ₃ [10]. Были рассмотрены различные причины явлений, такие как металлические кластеры, вторичные фазы, связанные магнитные поляроны, носители заряда и кислородные вакансии [2, 3, 5, 8, 9, 10, 11, 12, 13]. Последние гибридизуются вблизи поверхности наночастиц, приобретая магнитные свойства [12, 13]. В настоящее время объяснения по-прежнему спорны, и нет единого мнения об источнике ферромагнетизма. Поэтому исследовательская деятельность в этом направлении продолжается.

Среди сегнетоэлектриков в последнее время появились нанокристаллы (средний размер частиц 80 нм) танталата калия и ниобата калия, полученные по новой технологии оксигенации металлов (Ta или Nb) в расплавленном нитрате калия [14], методами магнитного резонанса и статического намагничивания. экспериментально установлено появление ферромагнитной подсистемы наряду с парамагнитной подсистемой [10, 15, 16]. Этот эффект отсутствует в более крупных кристаллах (размером> 200 нм) соединений, полученных по той же технологии. В объеме соединения немагнитны. Преднамеренное легирование танталатом калия (KNbO ₃ ) и ниобат калия (KTaO ₃ ) нанокристаллы железом и марганцем по отдельности привели к увеличению парамагнитной составляющей, в то время как ферромагнитная подсистема осталась неизменной [15, 16]. Было высказано предположение, что причиной появления магнитных свойств исходных сегнетоэлектрических нанокристаллов являются магнитные дефекты, которыми могут быть как атомы примеси железа, образующие металлические кластеры на поверхности наночастиц, так и вакансии кислорода [9]. Помимо упомянутых выше экспериментальных методов, это предположение было основано на данных элементного анализа и теоретических оценок.

Чтобы определить микроскопический механизм наблюдаемого явления, в данной работе мы анализируем ситуацию с помощью теории перколяции. Теория перколяции достаточно хорошо описывала ряд эффектов в неупорядоченных магнитных системах, раньше в ферродиэлектриках [17], позже в разбавленных магнитных полупроводниках (например, [18,19,20,21]). Магнитная подсистема рассматривается как связанный магнитный полярон в разбавленных полупроводниках. Эта модель была впервые предложена авторами [22], а затем развита авторами работ. [11, 23].

Предполагая доминирующую роль кислородных вакансий, мы используем модель связанных магнитных поляронов и находим радиус перколяции, при котором обменные взаимодействия между электронами, захваченными в кислородные вакансии, опосредованные ионами магнитной примеси, индуцируют поверхностное ферромагнитное упорядочение в сегнетоэлектрике KTaO ₃ и КНБО ₃ наночастицы.

Экспериментальные данные и модель ферромагнитного упорядочения

Для обоснования предложенной модели ферромагнитного упорядочения сначала изложим экспериментальные данные, полученные на сегнетоэлектрических наночастицах КTaO ₃ (KTO) и KNbO ₃ (KNO).

Исследуемые сегнетоэлектрические наночастицы являются номинально чистыми, т.е. в них специально не вводились легирующие примеси. Однако элементный анализ, выполненный с помощью атомно-эмиссионного спектрометра с индуктивно связанной плазмой (ICP-AES) Shimadzu ICPE-9000, показывает, что Fe присутствует в обоих материалах в виде неизбежной примеси в количестве 0,06 мол.% В КTaO ₃ и 0,008 мол.% в KNbO ₃ . Также известно, что кислородные вакансии всегда существуют в оксидных сегнетоэлектриках, таких как перовскит (общая формула ABO ₃ ), что приводит к некоторой нестехиометрии в этих соединениях. Экспериментально показано, что в нанокристаллах KTaO ₃ присутствуют две магнитные подсистемы (парамагнитная и ферромагнитная). и КНБО ₃ [9, 10, 15]. Парамагнитная подсистема состоит из отдельных невзаимодействующих магнитных Fe ³⁺ ионы в KTaO ₃ , и Fe ³⁺ и Mn ²⁺ ионы в KNbO ₃ . Кроме того, структура парамагнитного центра, определенная из измерений электронного парамагнитного резонанса (ЭПР), включает кислородную вакансию V (O), которая снижает симметрию центра [9, 15]. Для наглядности два типа парамагнитных центров, осевой и ромбической симметрии, в которых Fe ³⁺ ion заменяет Ta ⁵⁺ (или Nb ⁵⁺ ) иона, показаны на рис. 1. Для достижения компенсации заряда в структуре этих центров формируются одна (осевой центр) или две (ромбический центр) кислородные вакансии V (O).

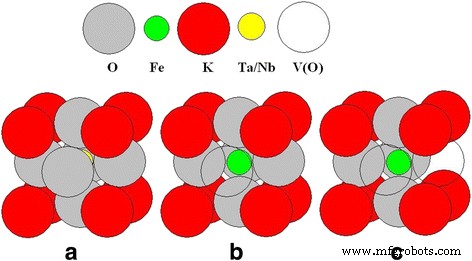
Модели низкосимметричных парамагнитных центров Fe ³⁺ в КТаО ₃ и КНБО ₃ нанокристаллы. а Элементарная ячейка без дефектов, b осевой Fe ³⁺ -V (O) в центре и c ромбический Fe ³⁺ -2 В (O) центр

В работах [9, 15] предполагается, что ферромагнитная подсистема представляет собой поверхностный кластер (кластеры), состоящий из атомов железа и кислородных вакансий. Термический отжиг в атмосфере кислорода, проведенный в работе [9], показывает, что кислородные вакансии определенно способствуют формированию ферромагнетизма в этих соединениях. С одной стороны, вакансии гибридизуются и становятся магнитными вблизи поверхности наночастиц [13]. С другой стороны, электроны, которые по своей природе возникают в нестехиометрических оксидах, часто захватываются кислородными вакансиями. В обоих случаях кислородная вакансия имеет спин S =½ и имеет соответствующий магнитный момент.

Наличие поверхностного ферромагнетизма подтверждено экспериментально с помощью атомно-силовой микроскопии (АСМ) в режиме градиента магнитного поля. Например, на рис. 2 представлены изображения поверхности, полученные для образца нанокристаллического KTaO ₃ . Магнитно-силовая микроскопия (MFM) проводилась с помощью сканирующего зондового микроскопа Dimension 3000 NanoScope IIIa для картирования пространственного изменения структуры намагниченности неплоскостной составляющей магнитного поля рассеяния KTaO ₃ поверхность образца. Градиенты магнитной силы были измерены с использованием двухпроходного метода (режим подъема), при котором топография сканировалась на первом проходе в режиме постукивания, а затем градиенты магнитного поля отображались на втором этапе с использованием сдвига частоты колебаний зонда, движущегося по поверхности (подъем высота составляла 300 нм). Покрытые кобальтом датчики магнитной силы Veeco (MESP) с коэрцитивной силой ~ 400 Э, магнитным моментом 1 · 10 ⁻¹³ emu и номинальный радиус вершины наконечника 25 нм. Перед измерениями зонд был намагничен с помощью сильного постоянного магнита с полем, направленным вдоль вертикальной оси наконечника.

Изображения поверхности с намагниченными участками в KTaO ₃ нанокристаллы. а Отображение градиента магнитного поля и b изображение рельефа поверхности

Кроме того, статические петли намагничивания были получены экспериментально при двух температурах для каждого соединения, при 290 и 150 К для KTaO ₃ и при 290 и 110 К для KNbO ₃ . Экспериментальные кривые намагничивания описываются формулой:

Здесь M _S намагниченность насыщения, H - статическое магнитное поле, а V ₀ - объем бесконечного (фактически замкнутого над поверхностью наночастицы) магнитного кластера. Намагниченность насыщения определялась по формуле (7) из [20]:

где S ₁ и S ₂ являются V (O) и Fe ³⁺ магнитные моменты (спины V (O) и Fe ³⁺ равны 1/2 и 5/2 соответственно), N ₁ и N ₂ - числа V (O) и Fe соответственно. Заданные значения N ₂ соответствуют концентрациям 0,06 мол.% для KTO и 0,008 мол.% для KNO, полученным в результате элементного анализа, значения N ₁ были определены соответственно. Результаты подгонки показаны на рис. 3. Для описания петель гистерезиса при малых магнитных полях мы использовали сдвиг формулы (2) на величину коэрцитивного поля, H _c . Параметры для каждой кривой приведены в таблице 1.

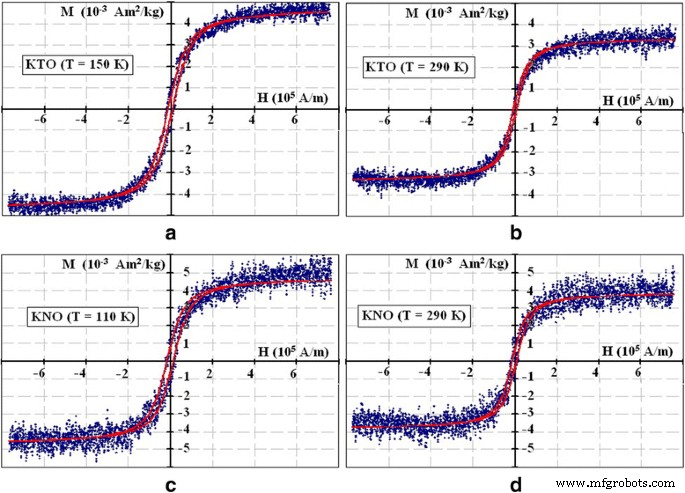
Кривые статического намагничивания. Кривые намагничивания в KTaO ₃ ( а , b ) и KNbO ₃ ( c , d ) наночастиц при T =150, 290, 110 и 290 К. Параметры подгонки перечислены в таблице 1

По количеству магнитных спинов, оцененному по данным ЭПР [10, 15], процентное соотношение парамагнитной и ферромагнитной подсистем составляет 14/86 в наноразмерном танталате калия и 40/60 для ниобата калия. Большее количество парамагнитных центров в ниобате калия обусловлено наличием неконтролируемой примеси марганца помимо примеси железа. Отметим, что количество магнитных спинов, образующих ферромагнитную подсистему, полученное из предыдущих экспериментов, недостаточно для установления дальнего магнитного порядка во всем объеме наночастиц. Поэтому мы предполагаем, что основной вклад в ферромагнетизм вносят магнитные спины, которые находятся вблизи поверхности частиц, а именно в подповерхностном слое, обогащенном дефектами. Как указано в [24], поверхностный слой, обогащенный полярными дефектами, имеет толщину около 10 постоянных решетки. С другой стороны, авторы работы [5]. [25] предполагают, что слой, обогащенный магнитными дефектами, в полубесконечном кристалле имеет толщину 1 постоянную решетки. Учитывая, что комплексы Fe ³⁺ -V (O) являются как полярными, так и магнитными дефектами, мы предполагаем, что приповерхностный дефектный слой имеет 5 постоянных решетки в наших расчетах. В КТаО ₃ и КНБО ₃ , слой соответствует 2 нм. Чтобы использовать условия перколяции, полученные в работе [17], мы предполагаем, что распределение дефектов в приповерхностном слое однородно. По данным просвечивающей электронной микроскопии (ПЭМ) (рис. 4, см. Также рис. 1 в [9] и рис. 2 в [26]) форма КTaO ₃ и КНБО ₃ наночастицы можно смоделировать в виде куба. Распределение кристаллитов по размерам в каждом соединении, полученное из данных ПЭМ, представлено на рис. 5.

ТЕМ изображение KTaO ₃ наночастицы

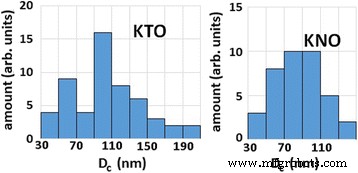
Распределение кристаллитов по размерам в KTaO ₃ и КНБО ₃

Основываясь на экспериментально полученных кривых намагничивания, в частности с учетом заданных количеств V (O) и Fe (см. Табл. 1), мы отмечаем доминирующую роль кислородных вакансий в намагничивании. При таком предположении обменное взаимодействие может быть инициировано электронами, захваченными в кислородные вакансии и опосредовано магнитными примесными ионами Fe. Такое взаимодействие рассмотрено в модели связанных магнитных поляронов. Эта модель была впервые предложена авторами [22] для описания возникновения ферромагнетизма в разбавленных магнитных полупроводниках. Схематично наша модель представлена ​​на рис. 6.

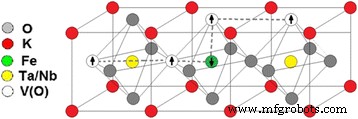
Модель дальнего магнитного порядка между электронами, захваченными в кислородные вакансии в нестехиометрическом KTaO ₃ / KNbO ₃ состав

Теоретическое моделирование в рамках подхода перколяции

Для определения критической концентрации полных дефектов, которая может приводить к образованию магнитных поляронов, мы используем перколяционный подход. Используя критерии теории перколяции, в работе [17] было показано, как математически устанавливается перколяционный порог дальнего магнитного порядка. Опуская детали подходов и принципов из работы. [17], мы сосредоточимся на особенностях, используемых в наших расчетах, и опишем общий ход расчета.

В соответствии с данными ПЭМ (см. Рис. 4), рассматриваемый KTaO ₃ и КНБО ₃ наночастицы можно смоделировать в виде куба. Использовалась кубическая решетка с постоянной решетки 0,4 нм. В приповерхностном слое толщиной 2 нм (то есть 5 элементарных ячеек) (фон приведен выше, см. Также [24] и [25]) со случайно распределенными дефектами, атомами Fe и кислородными вакансиями V (O), с учетом того, что распределение атомов железа равномерное. Согласно моделям осевого и ромбического центров (см. Рис. 1), наличие атома Fe в центре элементарной ячейки (когда он замещает атомы Nb или Ta ​​в KTaO ₃ или KNbO ₃ решетки) сопровождается появлением V (O) на краю (ах) ячейки. С некоторой вероятностью может появиться одна вакансия кислорода V (O) или две вакансии 2 V (O). В нашем случае вероятность составляет 50%, что соответствует экспериментально определенному соотношению аксиального (Fe-V (O)) и ромбического (Fe-2 V (O)) центров в KTaO ₃ и КНБО ₃ [9, 10, 15]. В наших расчетах дефекты моделировались сферами, при этом радиусы иона железа и кислородной вакансии равны r (Fe ³⁺ ) =0,064 нм и r (V (O)) =0,132 нм соответственно. Расстояние d Под дефектами понималось расстояние между поверхностями сфер, а не между их центрами. Зная координаты случайных дефектов, а именно атомов Fe и вакансий V (O), вычисляем расстояние d между ними. Результат распределения дефектов схематично показан на рис. 7.

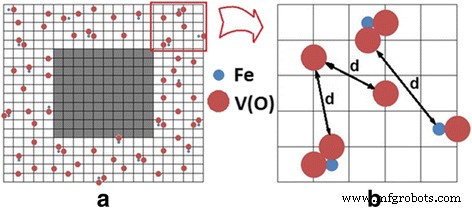
Распределение дефектов в поверхностном слое. а Светлая зона отображает слой подповерхностных дефектов. Серая зона отражает глубину наночастиц, где дефекты практически отсутствуют по сравнению с подповерхностным слоем. Пропорциональность между размером подповерхностной области дефекта и бездефектной внутренней сердцевины нарушена на этом рисунке для более четкого представления распределения дефектов в подповерхностном слое. Атомы Fe распределены равномерно по глубине дефектного слоя, кислородные вакансии V (O) расположены вблизи атомов Fe. б Масштаб дефектного слоя ( a ); г расстояние между дефектами

Согласно теории перколяции, дальний магнитный порядок в системе возникает, как только образуется бесконечный кластер (см., Например, с.235 в [17]). Расстояние между дефектами, которые образуют бесконечный кластер и, следовательно, удовлетворяют условию перколяции («порог перколяции»), определяется как радиус перколяции, R _perc . Для определения радиуса перколяции расчет проводился для наночастиц разного размера, чтобы гарантировать, что условие перколяции действительно выполняется. В этом случае соотношение между количеством магнитных дефектов в бесконечном кластере и общим количеством магнитных дефектов в системе остается неизменным в частицах разного размера. Размер наночастиц D × D × D элементарные ячейки, где D =20, 30, 40. Для определения зависимости радиуса перколяции от концентрации магнитных дефектов расчеты проводились для концентраций, представленных в таблице 2. Здесь n ₁ определяет концентрацию кислородных вакансий, не находящихся вблизи атомов Fe, n ₂ - концентрация атомов Fe, а n это общая концентрация дефектов. Обратите внимание, что мы проводим расчеты для двух случаев. Для случая I n ₁ / н ₂ =Const и n меняется. Для случая II n ₂ =Const и n ₁ варьируется.

Для определения радиуса перколяции R _perc , воспользуемся следующей процедурой. Для каждой концентрации мы устанавливаем определенное значение R который варьировался от 0,1 до 5,9 нм с шагом 0,2 нм. Расстояние d между дефектами сравнивали со значением R (для каждого R ценность). Таким образом, все магнитные дефекты делятся на две группы. Если расстояние d _ij между ближайшим i th и j количество дефектов меньше или равно R , т.е. d _ij ≤ R мы относим эти дефекты к группе, в которой существует магнитная связь между дефектами; в противном случае, если d _ij > R , мы относим такие дефекты к другой группе, где связь между дефектами отсутствует (т. е. нарушена). В результате расчета получаем матрицу m × м , элементы которого являются логическими значениями 1/0 (наличие / отсутствие связи между i th и j й дефекты). Здесь м - количество дефектов в подповерхностной части частицы определенного размера. Затем, используя принцип цепей Маркова, мы находим магнитные кластеры (т.е. совокупности точек {Fe, V (O)}), которые косвенно взаимодействуют. Для этого мы подняли вышеупомянутую м × м матрица в степени м и получаем новую матрицу m × м , элементы которого являются логическими значениями 1/0 (наличие / отсутствие опосредованного взаимодействия между i th и j й дефекты). Максимальная сумма строки матрицы соответствует размеру самого большого кластера для данного размера частицы. Аналогичные расчеты были выполнены для каждого значения R и размер наночастиц. Получены результаты для одной концентрации n =0,6117 нм ⁻³ перечислены в таблице 3. Область курсивом в таблице соответствует R = R _perc значение, которое является радиусом перколяции R _perc =1,7 нм. Радиус перколяции R _perc было найдено в соответствии с описанным выше порогом перколяции.

На рисунке 8 схематично показано образование бесконечного кластера из частиц разного размера.

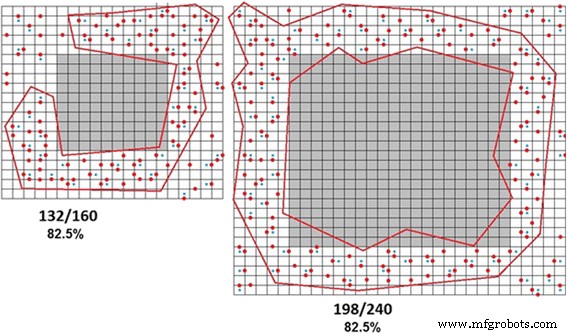
Бесконечное образование кластеров в частицах разного размера. Порог перколяции составляет 82,5% и определяется как процентное соотношение дефектов в кластере, не зависящее от размера частиц, как ожидалось.

Результаты и обсуждение

На рисунке 9а показана зависимость радиуса перколяции R _perc от концентрации дефектов для случая I, т.е. когда n ₁ / н ₂ =Const и n меняется. Сплошные кривые построены по формуле

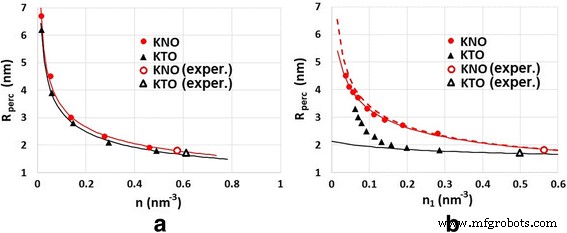
Радиус перколяции в зависимости от концентрации дефектов для двух случаев: a нет ₁ / н ₂ =Const, n меняется и b нет ₂ =Const, n ₁ меняется. Точки рассчитываются численно в рамках нашей модели, сплошные кривые построены по формуле (1). Точки, отмеченные метками, соответствуют изученным материалам (КТаО ₃ и КНБО ₃ )

с параметрами a =1,6 и 1,7 для KTO и KNO соответственно и b =0,25 нм как для KTO, так и для KNO. Первый член в формуле (3) согласуется с уравнением (4) в [3]. [20] для радиуса перколяции \ ({R} _ {\ mathrm {perc}} =\ frac {a} {\ sqrt [3] {n}}. \)

Значение R _perc - некое критическое значение, для R > R _perc , будет формироваться бесконечный кластер, что находится в пределах необходимого условия возникновения дальнего магнитного порядка в рамках теории перколяции. Мы предположили, что радиус R _perc то же самое для пар Fe-Fe, V (O) -V (O) и V (O) -Fe. Однако, основываясь на результатах расчетов и экспериментальных фактах, мы можем утверждать, что радиус R _perc не может быть меньше 1,6 нм для KTaO ₃ и 1,7 нм для KNbO ₃ .

Рассмотрим более подробно формулу (3). Физический смысл выражения \ (1 / \ sqrt [3] {n} \) - это расстояние между дефектами, участвующими в магнитном обмене для возникновения дальнего порядка. Значение a может быть как меньше, так и больше 1. Когда радиус R _perc соответствует среднему расстоянию между дефектами, значение a =1, и поэтому \ ({R} _ {\ mathrm {perc}} =1 / \ sqrt [3] {n} \). Когда количество случайных магнитных связей, которые образуются при взаимодействии дефектов на расстоянии меньше среднего, достаточно для образования бесконечного кластера, значение a меньше 1. Например, a =0,86 в работе [17]. Оказывается, R _perc в 1,6–1,7 раза превышает среднее расстояние между дефектами в нашем случае. Это можно объяснить следующим образом.

Значение среднего расстояния между дефектами имеет смысл для равномерного распределения дефектов в подповерхностном слое. Распределение атомов Fe считается квазиоднородным, но с учетом того, что атомы Fe расположены в центре ячейки, их положения являются дискретными пространственными координатами, что также влияет на величину a в уравнении 3, и расположение кислородных вакансий V (O) неоднородно, поскольку они всегда находятся рядом с атомами Fe (см. рис. 6). Таким образом, расстояние между атомами Fe намного больше, чем расстояние между атомом Fe и кислородной вакансией V (O). Следовательно, радиус R _perc фактически не зависит от среднего расстояния между всеми дефектами, но зависит от среднего расстояния между дефектами в различных элементарных ячейках (это может быть расстояние между Fe-Fe, V (O) -V (O), V (O) ) -Fe). Наличие кислородных вакансий вблизи атомов Fe несколько сокращает расстояние между дефектными ячейками из-за малости расстояния V (O) -Fe по сравнению с расстоянием Fe-Fe. Это означает, что в данном случае мы имеем дело со средним расстоянием между атомами Fe.

Вычитание второй составляющей b =0,25 нм в уравнении (3) можно объяснить следующим образом. Обычно расстояние между дефектами в этом уравнении определяется как расстояние между центрами дефектов, если дефект моделируется как точка. В наших расчетах R _perc определяется как расстояние между поверхностями сферы, на которой мы поместили дефект (ы). Итак, значение R _perc , оцениваемое как расстояние между поверхностями сфер, отличается от R _perc оценивается как расстояние между центрами не менее чем по сумме двух радиусов взаимодействующих дефектов. Сумма может варьироваться от 0,128 нм для взаимодействия Fe-Fe (фиг. 10a) до 0,264 нм для взаимодействия V (O) -V (O) (фиг. 10c). Кроме того, поскольку расстояние между атомом Fe и ближайшей вакансией V (O) намного меньше расчетного, требуется для установления связи между дефектами, в некоторых случаях R _perc можно определить как расстояние V (O) -Fe или V (O) -V (O) от разных ячеек (см. рис. 10b, c). Когда количество V (O) увеличивается, количество случаев, представленных на рис. 10b, c, соответственно увеличивается. Соответственно, рассчитанное значение b = 0,25 нм означает, что в основном обменное взаимодействие происходит непосредственно между электронами, захваченными в кислородные вакансии.

Уменьшение R _perc для взаимодействия между различными дефектами ( a - c ) по сравнению с равномерным распределением Fe ( синий ) атомов обусловлено наличием кислородных вакансий V (O) ( красный )

На рисунке 9б показана зависимость радиуса перколяции R _perc от концентрации дефектов для случая II, т.е. когда n ₂ =Const и n ₁ меняется. Здесь влияние атомов Fe возрастает как n ₁ уменьшается. Это более заметно для КТО (черная сплошная кривая на рис. 9б). Тем не менее, мы попытались подогнать расчетные данные по формуле (3) с параметрами a =0,66 и b =0,15 нм. Значение b указывает на то, что относительное количество прямых взаимодействий V (O) -V (O) уменьшается, тогда как количество косвенных взаимодействий через атомы Fe увеличивается.