Большие спин-зависимые термоэлектрические эффекты в взаимосвязанных нанопроводных сетях на основе NiFe

Введение

Термоэлектрические эффекты в материалах спинтроники активно изучаются в развивающейся области спиновой калоритроники из-за их уникальных физических свойств, включая спиновые эффекты Зеебека, термически генерируемый спиновый ток и крутящий момент с термической передачей спина [1–7]. Кроме того, особый интерес представляют термоэлектрические аналоги магниторезистивных эффектов в магнитных мультислоях, спиновых клапанах и туннельных переходах, такие как гигантские эффекты магнито-Зеебека и магнито-Пельтье, поскольку они могут быть использованы для магнитного управления тепловым потоком и термоэлектрических напряжения для утилизации отходящего тепла электронных схем [3, 8–13]. Большие зависящие от спина термоэлектрические эффекты, достигаемые за счет соответствующей модификации конфигураций намагниченности мультислоя с помощью внешнего магнитного поля, используют тот факт, что коэффициенты Зеебека для электронов со спином вверх и вниз значительно различаются. Это различие коэффициентов Зеебека приписывается обменному расщеплению d-зоны в переходных ферромагнитных (FM) металлах, как предполагалось в предыдущих работах, выполненных на разбавленных магнитных сплавах [14, 15]. При рассмотрении эффекта Пельтье это означает, что электроны со спином вверх и вниз переносят разное количество тепла. Недавно было продемонстрировано, что взаимосвязанные сети на основе магнитных нанопроволок (NW), изготовленные электрохимическим осаждением в трехмерных нанопористых полимерных пленках-хозяевах, обеспечивают привлекательный путь для создания легких, надежных, гибких и изменяемых спин-калоритронных устройств в различных форматах, отвечающих ключевым требованиям в области электрических и тепловых сетей. , механическая устойчивость [16, 17]. Кроме того, электрохимический синтез является мощным методом изготовления многокомпонентных нанопроволок из различных металлов из-за его инженерной простоты, универсальности и низкой стоимости [18–20]. В таких сетях с нанопроводами сантиметрового масштаба электрическая связь необходима для обеспечения протекания заряда по всем размеру образца. Система на основе нанопроволок преодолевает недостаточную надежность и воспроизводимость результатов, полученных в металлических наностолбиках и магнитных туннельных переходах [3, 9, 10, 12], что в основном может быть связано с сопротивлением теплового контакта между образцами нанометрового размера и тепловым сопротивлением. ванны, создающие температурный градиент. Сети из трехмерных нанопроволок открывают перспективы для гибких термоэлектрических генераторов, демонстрирующих чрезвычайно высокий коэффициент термоэлектрической мощности с магнитной модуляцией. Обычные термоэлектрические модули состоят из связанных термоэлектрических материалов или ветвей n- и p-типа. В то время как первоначальная работа была сосредоточена на системах ННК n-типа, сделанных из мультислоев Co / Cu и CoNi / Cu [16, 17], недавно было показано, что разбавленные сплавы NiCr являются многообещающими для изготовления термоэлектрических ветвей на основе нанопроволок p-типа [16, 17]. 21]. В данной работе мы сообщаем об экспериментальных результатах, полученных на других термоэлектрических пленках n-типа на основе связанных между собой сплавов Ni, NiFe и Ni ₈₀ Fe ₂₀ / Медные многослойные СЗ сети. Никель-железо - важный магнитно-мягкий материал, который широко используется в технологиях магнитного хранения данных. Сплавы NiFe с оптимизированным составом образцов также демонстрируют большую термоЭДС вблизи комнатной температуры. Кроме того, мультислои NiFe / Cu являются хорошо известными системами гигантского магнитосопротивления (ГМС) [22]. Физическое происхождение ГМС заключается в различных свойствах проводимости электронов со спином большинства и неосновности в магнитных мультислоях. Благодаря измерениям магнито-термоЭДС и использованию того факта, что архитектура с разветвленной нанопроволокой этих многослойных сетей NW позволяет электрические измерения в токе, перпендикулярном плоскости (CPP) геометрии, точное определение спин-зависимых коэффициентов Зеебека в пермаллое (Ni _{) 80} Fe ₂₀ ) получается.

Экспериментальные методы

Пористые мембраны из поликарбоната (ПК) с соединенными между собой порами были изготовлены путем экспонирования 22- μ пленку ПК толщиной m в двухэтапный процесс облучения [23, 24]. Топология мембран была определена путем воздействия на пленку первого этапа облучения под двумя фиксированными углами -25 ^∘ и +25 ^∘ относительно нормальной оси плоскости пленки. После поворота пленки ПК в плоскости на 90 ^∘ , второй этап облучения происходил при том же фиксированном угловом потоке облучения, чтобы окончательно сформировать трехмерную сеть наноканалов. Затем скрытые дорожки были подвергнуты химическому травлению в соответствии с ранее описанным протоколом [25] для получения трехмерных пористых мембран с порами диаметром 80 нм и объемной пористостью 3%. Затем шаблоны ПК были покрыты с одной стороны с использованием электронного испарителя с металлическим двухслойным слоем Cr (3 нм) / Au (400 нм), который служил катодом во время электрохимического осаждения. Сеть NW частично заполняет пористую 3D-мембрану ПК. ННК сплава NiFe контролируемого состава с содержанием Fe менее 40% были успешно выращены при комнатной температуре с использованием сульфатной ванны и осаждены при различных потенциалах [26]. Кроме того, электроосажденный Py (пермаллой, Ni ₈₀ Fe ₂₀ ) / Cu многослойные нанопроволоки были изготовлены из ванны с одним сульфатом, содержащей Ni ²⁺ , Fe ²⁺ , и Cu ²⁺ ионы с использованием метода импульсного электроосаждения, как описано в справ. [27]. Следуя процедуре, описанной в другом месте [18], скорость осаждения каждого металла определялась по времени заполнения пор. Толщина бислоев была установлена ​​равной 10 нм при примерно такой же толщине для слоев Py и Cu. Примесь Cu присутствует в пермаллое только в очень ограниченном количестве (менее 5%), как было оценено с помощью энергодисперсионного рентгеновского анализа (EDX). Микроструктура одиночных нанопроволок NiFe и NiFe / Cu, выращенных электроосаждением в нанопорах, ранее была исследована с помощью рентгеновской дифракции и аналитической просвечивающей электронной микроскопии [28]. Рисунок 1а иллюстрирует гибкость пленки спинового калоритронного устройства на основе взаимосвязанной сети нанопроволок. Пленка легко скручивается, не нарушая ее электрических свойств. Химическое растворение шаблона ПК с использованием дихлорметана приводит к взаимосвязанной металлической самоподдерживающейся структуре (вставка на рис. 1а), которая точно воспроизводит трехмерный пористый шаблон. Для проведения электрических и термоэлектрических измерений переноса катод был локально удален путем плазменного травления, чтобы создать двухзондовую конструкцию, подходящую для электрических измерений, как показано на рис. 1b, c [16, 29, 30]. В этой конфигурации ток напрямую вводится в разветвленную структуру CNW (длиной около 1 см) из нетравленных участков металлического катода, где электрические контакты непосредственно создаются краской Ag, и проходит через 20- мкм. Сеть NW толщиной м благодаря высокой степени электрической связности CNW. Более того, поскольку поток электрических и тепловых токов ограничен вдоль сегментов нанопроволоки, в случае многослойной структуры ток течет перпендикулярно плоскости слоев. Типичные значения сопротивления приготовленных образцов находятся в пределах нескольких десятков Ом. Для каждого образца входная мощность поддерживается ниже 0,1 μ . W, чтобы избежать самонагрева, и сопротивление было измерено в пределах его диапазона омического сопротивления с разрешением одна часть на 10 ⁵ . Тепловой поток создается резистивным элементом и термоэлектрическим напряжением Δ V создается разницей температур Δ Т между двумя металлическими электродами. Выводы напряжения были сделаны из тонких хромелевых проводов, и вклад выводов в измеренную термоэлектрическую мощность вычитался с использованием рекомендованных значений абсолютной термоЭДС хромеля P в базе данных термопар NIST ITS-90. Температурный градиент контролировался с помощью дифференциальной термопары малого диаметра типа E. При измерениях использовалась типичная разница температур 1 К. Для измерений магнитосопротивления (MR) и магнитотермоэдс (MTP) внешнее магнитное поле прикладывалось вдоль внеплоскостных (OOP) и плоскостных (IP) направлений сетчатых пленок NW (более подробную информацию см. В разделе термоэлектрические измерения. и поправочный коэффициент в Дополнительном файле 1).

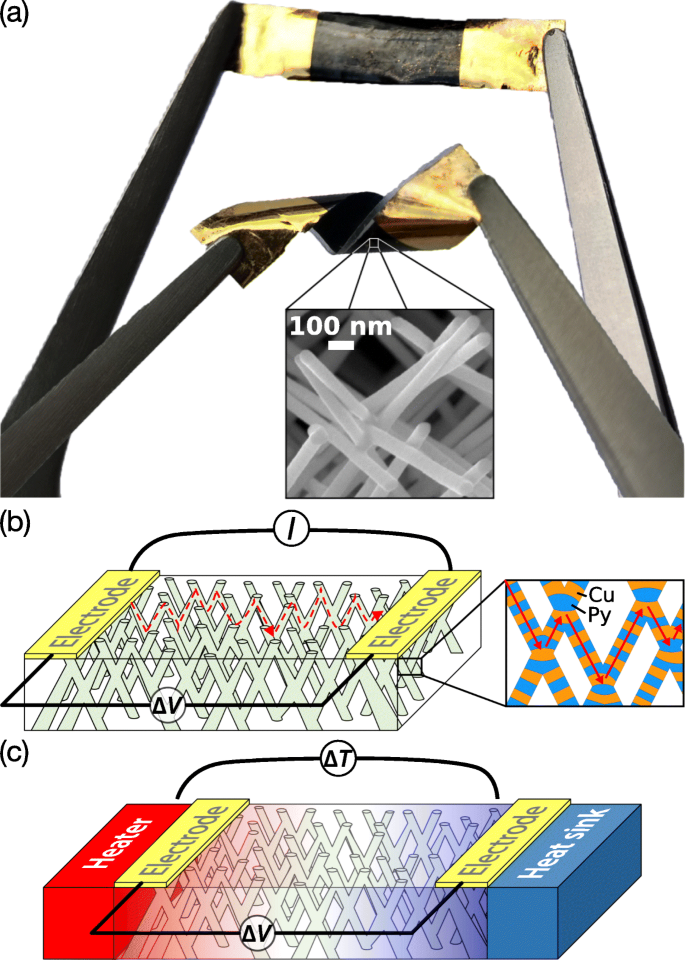
а Фотография гибкого спинового калоритронного устройства на основе сети из нанопроволок. На вставленном СЭМ-изображении показана разветвленная структура нанопроволоки диаметром ∼80 нм. Схематическое изображение конструкции электрода для электрического ( b ) и термоэлектрический ( c ) измерения взаимосвязанной сети NW. На вставке к рис. 1б схематически изображена многослойная структура Py / Cu. Красные стрелки обозначают направление тока. Цвет в c представляет собой созданный температурный профиль в сетях NW

Результаты и обсуждения

Абсолютная термоэлектрическая мощность при комнатной температуре (RT) сеток NW из чистого Ni и сплава NiFe, содержащих 20%, 30% и 40% Fe, показана на рис. 2а. Термоэдс непрерывно увеличивается с увеличением содержания Fe, достигая значений между –20 μ . В / К для чистого Ni примерно до –45 μ В / К для Ni ₆₀ Fe ₄₀ . Столбики ошибок на рис. 2а связаны с неопределенностями в составе сплавов, связанных с процессом гальваники. Эти результаты хорошо согласуются с экспериментальными данными, полученными на объемных сплавах NiFe [31]. Следовательно, сплавы NiFe с точно подобранным составом потенциально дают значительно более высокие коэффициенты Зеебека, чем чистые ферромагнитные металлы, такие как Co, и материалы термопар, такие как константан (Cu ₅₅ Ни ₄₅ : S ≈ -38 мкм В / К). Также отметим, что измеренное значение Py NWs ( S ≈ -37 μ V / K) очень похожи на приведенные в литературе объемные значения [32, 33]. Панели b и c на рис. 2 показывают зависимости сопротивления и термоЭДС сетей Ni и Py NW от магнитного поля при приложении поля в направлениях IP и OOP. Сопротивление и термоЭДС образцов Py и Ni ННК показывают одинаковые зависимости от магнитного поля в обоих направлениях. R ( H ) кривые хорошо соответствуют эффекту анизотропного магнитосопротивления, который обусловлен анизотропией спин-орбитального рассеяния в переходных ферромагнитных металлах. Этот эффект приводит к снижению удельного сопротивления при увеличении угла между направлением намагничивания и тока. Действительно, ток ограничен по сегментам NW, намагниченность насыщения в IP-направлении составляет средний угол ± 65 ^∘ с текущим. Напротив, когда намагниченность насыщается в направлении OOP, средний угол между намагниченностью и током намного меньше (± 25 ^∘ ). Следовательно, уменьшение сопротивления во внешнем магнитном поле усиливается, когда поле прикладывается в IP-направлении. Очевидно, что состояние с более низким сопротивлением, ожидаемое для перпендикулярной конфигурации между намагниченностью и током, не может быть достигнуто в таких сетях NW. Наблюдение, что абсолютное значение термоэдс увеличивается с увеличением поперечного магнитного поля как в сетках НП из Ni, так и сплава NiFe, также хорошо согласуется с предыдущими исследованиями, выполненными на одиночных НП [34]. На рис. 2d показаны величины магнитосопротивления и магнитотермоэдс, оцененные при RT в IP-направлении для сеток NW из чистого Ni и сплава NiFe. Здесь отношения MR и MTP определены как MR =( R ( H =0) - R ( H _сб )) / R ( H =0) и MTP =( S ( H =0) - S ( H _сб )) / S ( H =0), с R ( H _сб ) и S ( H _сб ) сопротивление и термоЭДС при H =10 кЭ соответственно. Для образцов сплава NiFe величина отношения MTP либо сравнима, либо меньше (Py) отношения MR. Такое меньшее значение отношения MTP относительно соответствующего отношения MR для сетки Py NW согласуется с измерениями, выполненными на тонких пленках Py [35]. Напротив, сеть Ni NW демонстрирует эффект MTP на –5%, намного больший, чем отношение MR, равное 1,5%. Этот результат хорошо согласуется с предыдущими измерениями, выполненными на одиночных Ni ННК, показывая такое же усиление эффекта MTP [34]. Интересно отметить, что для тонких пленок Ni наблюдаемая анизотропия коэффициента Зеебека имеет примерно такую ​​же величину, что и анизотропное МС (∼1.5%) [35]. Необходимы дальнейшие исследования, чтобы понять этот неожиданно улучшенный MTP для Ni NW.

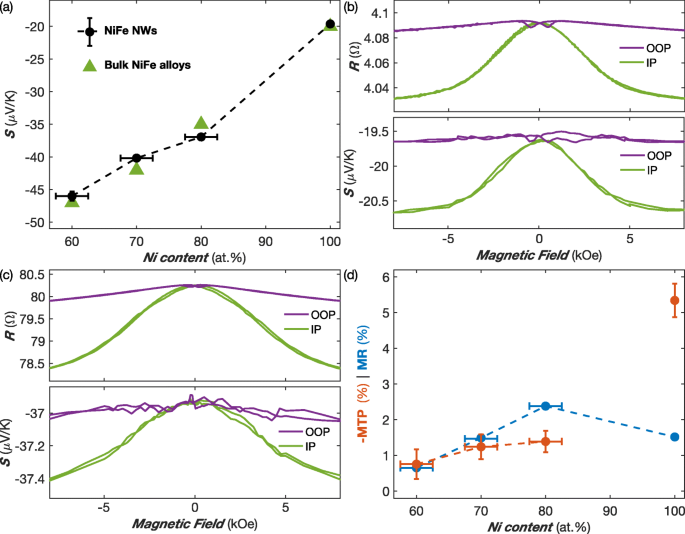
а Изменение коэффициента Зеебека в зависимости от содержания Ni в сетях NiFe NW (диаметр 80 нм) при комнатной температуре. Также приведены рекомендуемые значения для массивных сплавов [38]. б , c Изменение электрического сопротивления и коэффициента Зеебека Ni при комнатной температуре ( b ) и Py ( c ) NW образцы, полученные с приложенным полем в плоскости (IP) и вне плоскости (OOP) сетевой пленки NW. г Соотношения MR и MTP в зависимости от содержания Ni в сетях NiFe NW при RT

В многослойных слоях FM / Cu коэффициент Зеебека в направлении, перпендикулярном слоям, может быть рассчитан из соответствующих транспортных свойств с использованием правил Кирхгофа [36],

где S _{FM, Cu} и κ _{FM, Cu} представляют собой термоэдс и теплопроводность ферромагнитного материала и Cu и λ = t _FM / t _Cu соотношение толщины слоев FM и Cu. Согласно формуле. 1, S _⊥ в основном определяется большой термоЭДС металла FM при соотношении толщин λ не так уж мало, так как S _FM κ _Cu >> S _Cu κ _FM .

Напротив, коэффициент Зеебека многослойного пакета FM / Cu в направлении, параллельном слоям, определяется как

с ρ _FM и ρ _Cu как соответствующие удельные электрические сопротивления. В этом случае большая термоЭДС может быть получена только при соотношении толщин λ очень большой. Контрастное поведение между слоями, параллельным и перпендикулярным направлениям, показано на рис. 3а для мультислоев Py / Cu с использованием формул. 1 и 2, а также значения удельного сопротивления и термоэдс для объемного пермаллоя [32, 33, 37, 38] ( ρ _Py ≈ 25 мкм Ом см, S _Py =–35 мкм В / К) и медь ( ρ _Cu =1,6 мкм Ом см, S _Cu =1,7 мкм В / К), а также теплопроводности, оцененные по закону Видемана-Франца ( κ ρ = L Т , где T это температура и L - отношение Лоренца). Ожидается, что для массивного монокристалла Py относительно небольшой решеточный вклад в теплопроводность немного изменит расчетное значение. Хотя значения удельного электрического сопротивления и теплопроводности многослойных нанопроволок могут значительно отличаться от их соответствующих объемных составляющих, сохраняется такое же контрастное поведение между параллельным и перпендикулярным направлениями слоев. Таким образом, многослойные ННК с чередующимися стопками разнородных материалов, таких как Py и Cu (см. Рис. 3а), являются многообещающими кандидатами на роль хороших термоэлектрических материалов.

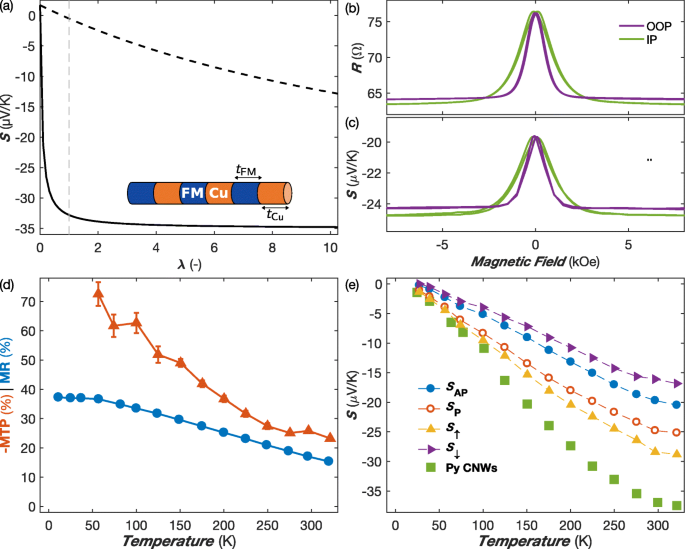
а Расчетная термоэдс для мультислоев Py / Cu в параллельном (пунктирная линия) и перпендикулярном (сплошная линия) направлениях слоя в зависимости от отношения толщин λ = t _Py / t _Cu используя уравнения. 1 и 2 и объемные значения транспортных коэффициентов. Серая пунктирная линия показывает значения для λ . =1; на вставке - многослойная стопка FM / Cu. б Изменение электрического сопротивления и коэффициента Зеебека сети Py / Cu NW при комнатной температуре в магнитных полях, приложенных в направлениях IP и OOP. c Коэффициент MR и MTP как функция температуры с полем, приложенным в плоскости сетчатых пленок NW. г Измеренные коэффициенты Зеебека при нулевом приложенном поле S _AP (синие полные кружки) и при насыщающем магнитном поле S _P (красные открытые кружки) вместе с соответствующим рассчитанным S _↑ (оранжевые треугольники) и S _↓ (фиолетовые треугольники) из уравнений. 5 и 6 (см. Текст). Также представлены данные, полученные на сетке Py NW (диаметр 80 нм) (зеленые квадраты). Планки погрешностей отражают неопределенность электрических и температурных измерений и устанавливаются равными двукратному стандартному отклонению, что составляет 95% отклонения данных

Как показано на рис. 3b, сопротивление и термоэдс сети Py / Cu NW показывают одинаковые зависимости магнитного поля вдоль направлений OOP и IP пленки сети NW. Легкая ось направлена ​​в направлении ООП с магнитным полем насыщения около 1,8 кЭ. Было обнаружено, что образец демонстрирует большие отклики GMR (с использованием текущего определения отношения GMR, в котором эффект MR нормализуется к состоянию с более низким сопротивлением R _P , т.е. GMR = R _AP / R _P −1, с R _AP и R _P как соответствующие сопротивления в высокоомном и низкоомном состояниях), достигая значений RT 20,5% и 19% в направлениях IP и OOP соответственно. Небольшая разница объясняется вкладом анизотропного магнитосопротивления. Как и ожидалось, измеренная термоЭДС RT на сети CPP-GMR Py / Cu NW в насыщенном состоянии ( S ≈ –25 мкм V / K вдоль IP-направления) лишь немного меньше, чем значение, обнаруженное в однородном образце Py. Напротив, коэффициенты Зеебека RT, указанные для мультислоев NiFe / Cu в геометрии CIP (∼-10 μ V / K) намного меньше [39]. В дальнейшем приводятся только измерения, полученные в плоскости сетчатых пленок ННК. Как показано на рис. 3c, абсолютное значение магнитотермоэдс MTP =( S _AP - С _P ) / S _AP , с S _AP и S _P соответствующие диффузионные термоЭДС в состояниях с высоким и низким сопротивлением, соответственно, монотонно возрастают с понижением температуры аналогично коэффициенту MR (определяемому как MR =( R _AP - R _P ) / R _AP ). Однако, хотя величина эффектов близка к RT, MTP демонстрирует выраженное усиление в низкотемпературном диапазоне. Такое поведение контрастирует с тем, что наблюдалось для сеток Co / Cu и CoNi / Cu NW, в которых наблюдается заметное падение MTP при низких температурах [16,17]. Около T =50 K, MTP достигает около 70% для образца Py / Cu, что в 2–3 раза больше, чем у сеток Co / Cu и CoNi / Cu NW. Отношение GMR при низких температурах (∼60%) лишь немного меньше, чем те, о которых сообщалось ранее для массивов параллельных ННК Py / Cu [27, 40], тем самым демонстрируя, что высокоэффективные гибкие пленки CPP-GMR на основе сетей ННК могут производиться этим простым и недорогим методом снизу вверх.

Используя простое рассмотрение параллельных токовых путей электронов со вращением вверх и вниз [41], соответствующие термоЭДС в состояниях с высоким и низким сопротивлением, S _AP и S _P , просто даются:

и:

где отдельные удельные сопротивления ρ _↑ и ρ _↓ и коэффициенты Зеебека S _↑ и S _↓ определены для мажоритарных и миноритарных спиновых каналов. Следовательно, зависящие от спина коэффициенты Зеебека, S _↑ и S _↓ можно выразить следующим образом [16]:

где β =( ρ _↓ - ρ _↑ ) / ( ρ _↓ + ρ _↑ ) обозначает коэффициент спиновой асимметрии удельного сопротивления. Приблизительная оценка β =0,6 при низких температурах с использованием β =MR ^1/2 находится в разумном согласии с предыдущими результатами экспериментов CPP-GMR, проведенных на мультислоях Py / Cu [42]. Из уравнений. 5 и 6, легко вывести, что S _↑ = S _P и S _↓ = S _AP в пределе чрезвычайно большого отношения MR ( β → 1). На рис. 3d показано изменение температуры S . _AP , S _P , S _↑ , и S _↓ . Ниже RT различные коэффициенты Зеебека уменьшаются почти линейно с понижением температуры, что указывает на преобладание диффузионной термоэдс. Данные, полученные на однородной сети Py NW, также показаны на рис. 3d для сравнения. Для пермаллоя ННК величина коэффициента Зеебека близка к расчетной для S _↑ , как и ожидалось из уравнения. 4. Значение RT для спин-зависимого коэффициента Зеебека Δ S = S _↑ - С _↓ –12,3 мкм V / K в сетке Py / Cu ННК больше, чем полученные ранее для ННК Co / Cu и CoNi / Cu [16,17]. Это также намного больше, чем косвенно оцененные из измерений, выполненных на наностолбиках Py / Cu / Py и клапане боковых спиновых устройств с использованием трехмерной конечно-элементной модели [3, 11]. В этих предыдущих экспериментах с наноструктурами Py / Cu было трудно определить и / или исключить контактное термическое сопротивление, основной источник ошибок, и для оценки градиента температуры по многослойным пакетам часто требовалось моделирование. Зависящие от спина коэффициенты Зеебека при комнатной температуре для различных магнитных многослойных систем приведены в таблице 1. В предыдущей работе предполагалось, что бесконечно большой MTP ожидается, когда произведение β η стремится к –1 [16]. Из приведенного выше анализа продукт β η около RT для нанопроволок Py / Cu оценивается около –0,1, что приводит к аналогичной величине MTP и MR, как показано на рис. 3d.

Заключение

Таким образом, крупномасштабный синтез однородных Ni, сплава NiFe и многослойных сетей нанопроволок Py / Cu был осуществлен путем электроосаждения в трехмерные пористые полимерные шаблоны. Мы обнаружили неожиданно высокое значение 5% для MTP Ni NW по сравнению с MR (~ 1,5%). Сети из нанопроволок из сплава NiFe демонстрируют большую термоэдс, примерно до -45 μ В / К для Ni ₆₀ Fe ₄₀ при комнатной температуре. ННК Py / Cu демонстрируют гигантское магнитосопротивление и магнитотермоэлектрические эффекты в геометрии перпендикулярно плоскости тока, которая превышает 50% при низких температурах. Мы также обнаружили большой зависящий от спина коэффициент Зеебека –12,3 μ V / K при комнатной температуре, что выше, чем ранее сообщалось о металлических магнитных многослойных слоях. Благодаря простоте изготовления геометрически сконструированных магнитных нанопроволок и многослойных материалов путем электроосаждения, а также их превосходным электрическим и термоэлектрическим свойствам, эти трехмерные сети NW обладают большим потенциалом для использования в качестве чрезвычайно легких и гибких устройств спиновой калоритроники. Такие эффекты могут быть применены, например, путем использования и преобразования энергии отходящего тепла, образующегося в электронных устройствах, или, наоборот, для создания решений для активного охлаждения электронных устройств.

Доступность данных и материалов

Наборы данных, использованные и / или проанализированные в ходе текущего исследования, доступны у соответствующего автора по разумному запросу.