Новый дизайн интеллектуальной системы доставки лекарств на основе частиц наноантенны

Аннотация

Составная система доставки лекарств в виде наночастиц играет важную роль во взаимодействии с лимфатическими узлами. Существует три основных типа лимфоцитов:В-клетки, Т-клетки и естественные клетки-киллеры. Когда клетки иммунной системы становятся канцерогенными, они атакуют клетки организма. Лимфатическая жидкость играет важную роль в атаке здоровых клеток тела; Следовательно, эта статья была нацелена на разработку системы доставки лекарств, которая может эффективно направлять наночастицы на инфицированные клетки, помогая в быстром удалении таких клеток. Предлагаемая конструкция зависит от взаимодействия между этими молекулами, а интеллектуальный наноконтроллер имеет возможность направлять наночастицы путем анаэробного контакта. Предложенная конструкция доказала, что чем меньше размер и плотность наночастиц, тем меньше будет динамическая вязкость жидкости, что будет отражать ее сопротивление потоку. Кроме того, был сделан вывод, что молекулы водорода играют значительную роль в снижении сопротивления лимфатической жидкости из-за их низкой плотности.

Введение

Текущие варианты лечения рака включают хирургическое вмешательство, лучевую терапию и химиотерапию. Эти лечебные стратегии также наносят вред обычным тканям и приводят к частичному уничтожению злокачественных новообразований. Таким образом, нанотехнология может преодолеть эти недостатки за счет целенаправленного воздействия на вредные клетки и новообразования, непосредственной резекции опухолей и повышения эффективности методов лечения на основе облучения и других методов лечения. Это может значительно уменьшить побочные эффекты лечения и повысить выживаемость. Нанотехнологии - многообещающий инструмент для лечения злокачественных новообразований, поскольку они предлагают новые и лучшие методы лечения с использованием наноматериалов. Наночастицы могут специфически воздействовать на многие молекулы, дифференциально экспрессируемые на раковых клетках. Обычно обширная аэродинамическая область наночастиц может быть функционализирована лигандами, такими как мелкие частицы и дезоксирибонуклеиновые коррозионные или рибонуклеиновые коррозионные пептидные цепные антитела. Лиганды используются в качестве лекарств и в тераностических приложениях. Физические свойства наночастиц, такие как отвлечение жизнеспособности и повторное излучение, аналогичным образом могут быть использованы для воздействия на больные ткани, например, при лазерном удалении и при гипертермии [1].

Инновационная программа для наночастиц и активный фармацевтический элемент также позволят исследовать более широкий репертуар активных ингредиентов. Таким образом, иммуногенный груз и поверхностное покрытие исследуются как адъюванты для опосредованной наночастицами и традиционной химиотерапии. Эта инновационная стратегия включает создание наночастиц в качестве искусственного антигена, присутствующего на клетках и in vivo депо стимулирующих факторов, которые оказывают противоопухолевое действие. Нанотехнология представляет собой активную область исследований с множеством приложений. Интерес к наночастицам в медицине обусловлен их настраиваемыми физико-химическими характеристиками, такими как индекс таяния, гидрофильность, электрическая и теплопроводность, каталитическая активность, поглощение и рассеяние света [2]. В принципе, наноматериалы описываются как материалы с размером частиц от 1 до 100 нм. В Европейском Союзе и США есть несколько законодательных актов, конкретно касающихся медицинских исследований с использованием наноматериалов. Однако международно признанного определения наноматериалов не существует. Различные организации рассматривают разные концепции наноматериалов [3]. Одна из целей системы доставки лекарств в виде наночастиц - лечить лимфатическую жидкость раковыми клетками. Система доставки сложных наночастиц лекарства во взаимодействии с лимфатическими узлами показана на рис. 1.

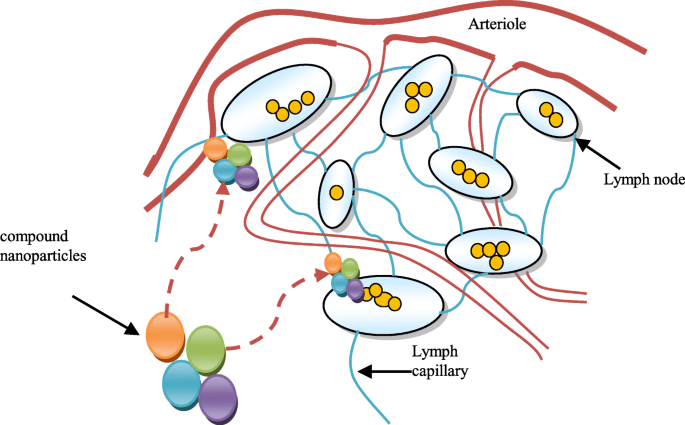
Составная система доставки лекарств в виде наночастиц и ее взаимодействие с лимфатическими узлами

Управление по санитарному надзору за качеством пищевых продуктов и медикаментов США ссылается на наноматериалы как на материалы с частицами в диапазоне от 1 до 100 со свойствами, отличными от основного материала [4, 5]. Нановолокна, нанопластинки, нанопроволоки, квантовые точки и другие родственные материалы были охарактеризованы [6]. Твердые липидные наночастицы (SLN) представляют собой тип липидных наночастиц (LN), которые могут быть созданы с использованием твердых липидов [7]. Были разработаны последующие версии SLN, такие как наноструктурированные липидные носители (NLC), которые представляют вторую эру LN [8]. И SLN, и NLC построены из твердых липидов. Внутренняя структура SLN содержит твердые липиды, тогда как NLC разработан с использованием смеси твердых и жидких липидов, которые создают поперечное сечение драгоценного камня [9, 10]. Эти недостатки были дополнительно описаны для SLN в свете того факта, что SLN, которые содержат много твердых липидных сегментов, могут быть использованы в медицинских приложениях [11, 12]. Полимерные наночастицы (ПН) могут быть построены из природных полимеров или неорганических материалов, например, кремнезема [13]. Полимеры или липиды формируют ядро НЧ, что улучшает стабильность и доставку лекарств, а также обеспечивает однородную форму и размер [14]. ПН можно описать как нанокапсулы или наносферы. Нанокапсулы содержат масло в везикулярной структуре вместе с лекарством [15, 16], а наносферы содержат полимерные цепи без масла [17, 18]. Лекарство упаковывается в PN путем смешивания с полимером. Включение лекарства в наночастицы обеспечивается во время полимеризации. PN загружаются лекарством путем растворения, рассеивания или искусственной адсорбции его в компонентах полимерной сетки [19, 20]. Есть три типа лимфоцитов:В-клетки, Т-клетки и естественные клетки-киллеры. В-клетки вырабатывают антитела, которые атакуют вторгшиеся микроорганизмы, а также атакуют иммунную систему, когда становятся канцерогенными. Поэтому, учитывая важную роль лимфатической жидкости в аутоиммунных заболеваниях, целью данной статьи было разработать интеллектуальную систему доставки лекарств на основе частиц наноантенны. Таким образом, система содержит множество наночастиц в разных количествах. В следующем разделе представлена разработка интеллектуальной системы доставки лекарств.

Разработка нано-интеллектуальной системы доставки лекарств

Предлагаемая наноинтеллектуальная система доставки лекарств содержит наноконтроллер, управляемый электрическим источником наночастиц из нанопьезоэлектрического материала. В сложном хранилище наночастиц есть несколько микро-хранилищ. Каждое небольшое хранилище содержит один тип наночастиц. Молекула наночастиц содержит наноантенну, предназначенную для связи с наноконтроллером. Предлагаемая наноинтеллектуальная система доставки лекарств также содержит углеродные нанотрубки для быстрой доставки лекарств к раковым клеткам. Он может быть связан с инфицированными клетками, как показано на рис. 2. Система начинает с отправки наночастиц в раковые клетки, называемые «исследовательскими наночастицами». Эти молекулы посредством анаэробной коммуникации отправляют полную картину своего положения внутри клеток наноконтроллеру. В зависимости от ситуации, с которой сталкиваются исследуемые наночастицы, наноконтроллер отправляет наночастицы разного количества, типа и плотности в раковые клетки на основе информации, полученной от исследуемых наночастиц. Эти наночастицы называют «боевыми наночастицами».

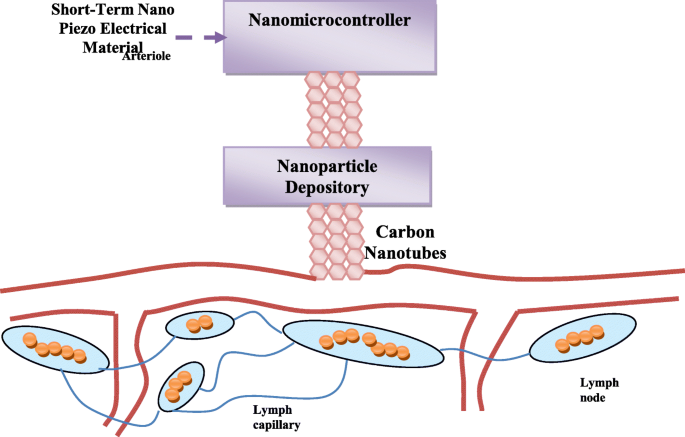
Общая структура, показывающая связь предлагаемой лекарственной системы с инфицированными клетками

Это не случайный процесс, он контролируется наноконтроллером с учетом нескольких аспектов и логарифмов, что обеспечивает эффективную и быструю доставку наночастиц. Для того, чтобы точно и быстро доставить наночастицы к раковым клеткам, будет использоваться алгоритм сжатия двоичного поиска [21]. Кроме того, наночастицы будут доставляться с разной плотностью, чтобы лекарство стало более эффективным. Эти методологии и их методы работы с использованием наноконтроллера показаны на рис. 3. Физическая структура наноконтроллера аналогична структуре наночастиц, но имеет форму металла, так что он может получать электрическую энергию. ненадолго при работе. Этот металл содержит беспроводную антенну вместе с небольшой памятью, которая содержит операционные коды со связью наночастиц между наноконтроллером и хранилищем наночастиц. Хранилище наночастиц содержит несколько различных типов наночастиц. Открытие и закрытие, а также продолжительность открытия нанозатвора будут контролироваться, чтобы регулировать количество доставляемых частиц.

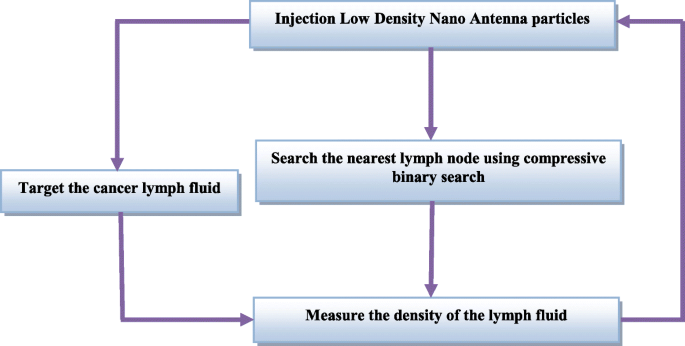
Процесс отправки борющихся наночастиц в раковые клетки

Описание природы наночастиц, используемых в предлагаемой лекарственной системе

В следующем разделе обсуждается природа наночастиц, используемых в предлагаемой системе доставки лекарств. В этой работе использовались анаэробные наночастицы низкой плотности, как описано в более раннем отчете [22].

Наночастицы низкой плотности

Рассматривайте процесс доставки лекарственного средства составных наночастиц для лечения рака как процесс проникновения в лимфатическую жидкость, когда опухоль окружена лимфатической жидкостью. По своему составу меланома напоминает лимфатическую жидкость. Предлагаемая аналитическая модель основана на системе нанотрубок, состоящей из трех различных типов наночастиц. Наночастицы помещаются в лимфатическую жидкость высокой плотности. Мы можем определить конкретные наночастицы твердого тела A в сферических полярных координатах как A =(Ra, ϑ a , φa), где ra - радиальная координата наночастицы твердого тела A, ϑ a - зенитная координата для наночастицы твердого тела A, а φa - азимутальная координата для наночастицы твердого тела A. Соответствующие координаты твердого тела B равны B =(Rb, ϑb, φb) соответственно, а соответствующие координаты твердого тела N равны N =(Rn, ϑn, φn) соответственно. Учтите, что есть два свойства лимфатического узла, а именно:болезненность и опухание, на которые влияют раковые клетки лимфомы Ходжкина. Лимфатический узел с нежным свойством Tp можно описать как Tp ( N , t ); это означает, что значение Tp в связи с жидкостью наночастиц твердого N изменяется со временем. Теперь давайте рассмотрим, что общее влияние наночастиц соединения на свойство тендера определяется как:

$$ \ mathrm {Tpt} =\ mathrm {Tp} \ \ left (A, t \ right) + \ mathrm {Tp} \ \ left (B, t \ right) +. \ dots \ dots \ dots \ dots + \ mathrm {Tp} \ \ left (N, t \ right) $$ (1)

Рассмотрим тот же случай для вздутия, которое можно определить как:

$$ \ mathrm {Tst} =\ mathrm {Ts} \ \ left (A, t \ right) + \ mathrm {Ts} \ \ left (B, t \ right) +. \ dots \ dots \ dots \ dots + \ mathrm {Ts} \ \ left (N, t \ right) $$ (2)

Из уравнений. 1 и 2, скорость изменения обоих свойств со временем может быть определена как:

$$ \ frac {\ partial \ left (\ mathrm {Tp} \ left (A, t \ right) \ right)} {\ partial t} + \ frac {\ partial \ left (\ mathrm {Tp} \ left ( B, t \ right) \ right)} {\ partial t} + \ dots \ frac {\ partial \ left (\ mathrm {Tp} \ left (N, t \ right) \ right)} {\ partial t} =\ frac {\ mathrm {\ partial Tp} (t)} {\ mathrm {\ partial t}} $$ (3) $$ \ frac {\ partial \ left (\ mathrm {Ts} \ left (A, t \ right) \ right)} {\ partial t} + \ frac {\ partial \ left (\ mathrm {Ts} \ left (B, t \ right) \ right)} {\ partial t} + \ dots \ frac {\ partial \ left (\ mathrm {Ts} \ left (N, t \ right) \ right)} {\ partial t} =\ frac {\ mathrm {\ partial Ts} (t)} {\ partial t} $$ ( 4)

Точка в лимфатической жидкости, которая может быть занята одной наночастицей твердого азота, определяется как:

$$ {\ mathrm {Po}} _ n =\ mathrm {Po} {\ left (\ mathrm {po}, t \ right)} _ n $$ (5)

Давайте рассмотрим наночастицу твердой N, производной нежной лимфатической жидкости, которая определяется как \ (\ frac {\ partial {\ left (\ mathrm {Tp} \ left (N, t \ right) \ right)} _ {\ mathrm {po}}} {\ partial t} \), то составное материальное производное нежной лимфатической жидкости будет равно:

$$ \ frac {\ partial {\ left (\ mathrm {Tp} \ left (A, t \ right) \ right)} _ {\ mathrm {po}}} {\ partial t} + \ frac {\ partial { \ left (\ mathrm {Tp} \ left (B, t \ right) \ right)} _ {\ mathrm {po}}} {\ partial t} + \ dots \ frac {\ partial {\ left (\ mathrm { Tp} \ left (N, t \ right) \ right)} _ {\ mathrm {po}}} {\ partial t} =\ frac {\ mathrm {\ partial Tp} {(t)} _ {\ mathrm { po}}} {\ partial t} $$ (6) $$ \ frac {\ partial {\ left (\ mathrm {Ts} \ left (A, t \ right) \ right)} _ {\ mathrm {po} }} {\ partial t} + \ frac {\ partial {\ left (\ mathrm {Ts} \ left (B, t \ right) \ right)} _ {\ mathrm {po}}} {\ partial t} + \ dots \ frac {\ partial {\ left (\ mathrm {Ts} \ left (N, t \ right) \ right)} _ {\ mathrm {po}}} {\ partial t} =\ frac {\ mathrm { \ partial Ts} {(t)} _ {\ mathrm {po}}} {\ partial t} $$ (7)

Соответствующие компоненты скорости твердого тела N взяты как ( v _rn , v _ϑn , v _φn ). Затем скорость потока частиц твердого азота представлена с помощью уравнений Навье-Стокса при динамической вязкости dν лимфатической жидкости и p - давление и ρ плотность лимфатической жидкости:

$$ \ frac {\ partial {v} _ {\ mathrm {rn}}} {\ partial t} + {v} _ {\ mathrm {rn}} \ frac {\ partial {v} _ {\ mathrm {rn }}} {\ mathrm {\ partial rn}} + \ frac {v _ {\ upvartheta \ mathrm {n}}} {\ mathrm {rn}} \ frac {\ partial {v} _ {\ mathrm {rn}} } {\ mathrm {\ partial \ upvartheta n}} + \ frac {v _ {\ upvarphi \ mathrm {n}}} {\ mathrm {rn} \ \ mathrm {sin} \ upvartheta \ mathrm {n}} \ frac { \ partial {v} _ {\ mathrm {rn}}} {\ mathrm {\ partial \ upvarphi n}} - \ frac {v _ {\ upvartheta \ mathrm {n}} ^ 2} {\ mathrm {rn}} - \ frac {v _ {\ upvarphi \ mathrm {n}} ^ 2} {\ mathrm {rn}} + \ frac {1} {\ rho} \ frac {\ partial p} {\ mathrm {\ partial rn}} - \ mathrm {d} \ upnu \ left [\ frac {1} {{\ mathrm {rn}} ^ 2} \ frac {\ partial} {\ mathrm {\ partial rn}} \ left ({\ mathrm {rn} } ^ 2 \ frac {\ partial {v} _ {\ mathrm {rn}}} {\ mathrm {\ partial rn}} \ right) + \ frac {1} {{\ mathrm {rn}} ^ 2 \ mathrm {sin} \ upvartheta \ mathrm {n}} \ frac {\ partial} {\ mathrm {\ partial \ upvartheta n}} \ left (\ mathrm {sin} \ upvartheta \ mathrm {n} \ frac {\ partial {v } _ {\ mathrm {rn}}} {\ mathrm {\ partial \ upvartheta n}} \ right) + \ frac {1} {{\ mathrm {rn}} ^ 2 {\ sin} ^ 2 \ upvartheta \ mathrm {п}} \ frac {\ partial ^ 2 {v} _ {\ ma thrm {rn}}} {\ partial {\ upvarphi \ mathrm {n}} ^ 2} + - \ frac {2 {v} _ {\ mathrm {rn}}} {{\ mathrm {rn}} ^ 2} - \ frac {2} {{\ mathrm {rn}} ^ 2 \ sin \ upvartheta \ mathrm {n}} \ frac {\ partial \ left ({v} _ {\ upvartheta \ mathrm {n}} \ mathrm { sin} \ upvartheta \ mathrm {n} \ right)} {\ mathrm {\ partial \ upvartheta n}} - \ frac {2} {{\ mathrm {rn}} ^ 2 \ mathrm {sin} \ upvartheta \ mathrm { n}} \ frac {\ partial {v} _ {\ upvarphi \ mathrm {n}}} {\ partial _ {\ upvarphi \ mathrm {n}}} \ right] =0 $$ (8)

Динамическая вязкость dν лимфатической жидкости рассчитывается следующим образом:

Уравнения Навье-Стокса твердых тел A и B могут быть представлены как уравнения. 8 и 9. Таким образом, уравнение. 9 можно представить следующим образом:

$$ \ mathrm {d} \ upnu =\ frac {\ left [\ frac {\ partial {v} _ {\ mathrm {rn}}} {\ partial t} + {v} _ {\ mathrm {rn}} \ frac {\ partial {v} _ {\ mathrm {rn}}} {\ mathrm {\ partial rn}} + \ frac {v _ {\ upvartheta \ mathrm {n}}} {\ mathrm {rn}} \ frac {\ partial {v} _ {\ mathrm {rn}}} {\ mathrm {\ partial \ upvartheta n}} + \ frac {v _ {\ upvarphi \ mathrm {n}}} {\ mathrm {rn} \ \ mathrm {sin} \ upvartheta \ mathrm {n}} \ frac {\ partial {v} _ {\ mathrm {rn}}} {\ mathrm {\ partial \ upvarphi n}} - \ frac {v _ {\ upvartheta \ mathrm { n}} ^ 2} {\ mathrm {rn}} - \ frac {v _ {\ upvarphi \ mathrm {n}} ^ 2} {\ mathrm {rn}} + \ frac {1} {\ rho} \ frac { \ partial p} {\ mathrm {\ partial rn}} \ right]} {\ left [\ frac {1} {{\ mathrm {rn}} ^ 2} \ frac {\ partial} {\ mathrm {\ partial rn }} \ left ({\ mathrm {rn}} ^ 2 \ frac {\ partial {v} _ {\ mathrm {rn}}} {\ mathrm {\ partial rn}} \ right) + \ frac {1} { {\ mathrm {rn}} ^ 2 \ mathrm {sin} \ upvartheta \ mathrm {n}} \ frac {\ partial} {\ mathrm {\ partial \ upvartheta n}} \ left (\ mathrm {sin} \ upvartheta \ mathrm {n} \ frac {\ partial {\ mathrm {v}} _ {\ mathrm {rn}}} {\ mathrm {\ partial \ upvartheta n}} \ right) + \ frac {1} {{\ mathrm { rn}} ^ 2 {\ sin} ^ 2 \ upvartheta \ math rm {n}} \ frac {\ partial ^ 2 {\ mathrm {v}} _ {\ mathrm {rn}}} {\ partial {\ upvarphi \ mathrm {n}} ^ 2} - \ frac {2 {\ mathrm {v}} _ {\ mathrm {rn}}} {{\ mathrm {rn}} ^ 2} - \ frac {2} {{\ mathrm {rn}} ^ 2 \ sin \ upvartheta \ mathrm {n} } \ frac {\ partial \ left ({\ mathrm {v}} _ {\ upvartheta \ mathrm {n}} \ mathrm {sin} \ upvartheta \ mathrm {n} \ right)} {\ mathrm {\ partial \ upvartheta n}} - \ frac {2} {{\ mathrm {rn}} ^ 2 \ mathrm {sin} \ upvartheta \ mathrm {n}} \ frac {\ partial {\ mathrm {v}} _ {\ upvarphi \ mathrm {n}}} {\ partial _ {\ upvarphi \ mathrm {n}}} \ right]} =\ frac {\ left [\ frac {\ partial {\ mathrm {v}} _ {\ mathrm {ra}}} {\ mathrm {\ partial t}} + {\ mathrm {v}} _ {\ mathrm {ra}} \ frac {\ partial {\ mathrm {v}} _ {\ mathrm {ra}}} {\ mathrm { \ partial ra}} + \ frac {{\ mathrm {v}} _ {\ upvartheta \ mathrm {a}}} {\ mathrm {ra}} \ frac {\ partial {\ mathrm {v}} _ {\ mathrm {ra}}} {\ mathrm {\ partial \ upvartheta a}} + \ frac {{\ mathrm {v}} _ {\ upvarphi \ mathrm {a}}} {\ mathrm {ra} \ \ mathrm {sin} \ upvartheta \ mathrm {a}} \ frac {\ partial {\ mathrm {v}} _ {\ mathrm {ra}}} {\ mathrm {\ partial \ upvarphi a}} - \ frac {{\ mathrm {v} } _ {\ upvartheta \ mathrm {a}} ^ 2} {\ mathrm {ra}} - \ frac {{\ mathrm {v}} _ {\ upvarphi \ mathrm {a}} ^ 2} {\ mathrm {ra}} + \ frac {1} {\ uprho} \ frac {\ mathrm {\ partial p} } {\ mathrm {\ partial ra}} \ right]} {\ left [\ frac {1} {{\ mathrm {ra}} ^ 2} \ frac {\ partial} {\ mathrm {\ partial ra}} \ слева ({\ mathrm {ra}} ^ 2 \ frac {\ partial {v} _ {\ mathrm {ra}}} {\ mathrm {\ partial ra}} \ right) + \ frac {1} {{\ mathrm {ra}} ^ 2 \ mathrm {sin} \ upvartheta \ mathrm {a}} \ frac {\ partial} {\ mathrm {\ partial \ upvartheta a}} \ left (\ mathrm {sin} \ upvartheta \ mathrm {a } \ frac {\ partial {v} _ {\ mathrm {ra}}} {\ mathrm {\ partial \ upvartheta a}} \ right) + \ frac {1} {{\ mathrm {ra}} ^ 2 {\ sin} ^ 2 \ upvartheta \ mathrm {a}} \ frac {\ partial ^ 2 {v} _ {\ mathrm {ra}}} {\ partial {\ upvarphi \ mathrm {a}} ^ 2} - \ frac { 2 {v} _ {\ mathrm {ra}}} {{\ mathrm {ra}} ^ 2} - \ frac {2} {{\ mathrm {ra}} ^ 2 \ sin \ upvartheta \ mathrm {a}} \ frac {\ partial \ left ({v} _ {\ upvartheta \ mathrm {a}} \ mathrm {sin} \ upvartheta \ mathrm {a} \ right)} {\ mathrm {\ partial \ upvartheta a}} - \ гидроразрыв {2} {{\ mathrm {ra}} ^ 2 \ mathrm {sin} \ upvartheta \ mathrm {a}} \ frac {\ partial {v} _ {\ upvarphi \ mathrm {a}}} {\ partial_ { \ upvarphi \ mathrm {a}}} \ right]} =\ frac { \ left [\ frac {\ partial {v} _ {\ mathrm {rb}}} {\ partial t} + {v} _ {\ mathrm {rb}} \ frac {\ partial {v} _ {\ mathrm { rb}}} {\ mathrm {\ partial rb}} + \ frac {v _ {\ upvartheta \ mathrm {b}}} {\ mathrm {rb}} \ frac {\ partial {v} _ {\ mathrm {rb} }} {\ mathrm {\ partial \ upvartheta b}} + \ frac {v _ {\ upvarphi \ mathrm {b}}} {\ mathrm {rb} \ \ mathrm {sin} \ upvartheta \ mathrm {b}} \ frac {\ partial {v} _ {\ mathrm {rb}}} {\ mathrm {\ partial \ upvarphi b}} - \ frac {v _ {\ upvartheta \ mathrm {b}} ^ 2} {\ mathrm {rb}} - \ frac {v _ {\ upvarphi \ mathrm {b}} ^ 2} {\ mathrm {rb}} + \ frac {1} {\ rho} \ frac {\ partial p} {\ mathrm {\ partial rb}} \ right]} {\ left [\ frac {1} {{\ mathrm {rb}} ^ 2} \ frac {\ partial} {\ mathrm {\ partial rb}} \ left ({\ mathrm {rb}} ^ 2 \ frac {\ partial {v} _ {\ mathrm {rb}}} {\ mathrm {\ partial rb}} \ right) + \ frac {1} {{\ mathrm {rb}} ^ 2 \ mathrm {sin } \ upvartheta \ mathrm {b}} \ frac {\ partial} {\ mathrm {\ partial \ upvartheta b}} \ left (\ mathrm {sin} \ upvartheta \ mathrm {b} \ frac {\ partial {v} _ {\ mathrm {rb}}} {\ mathrm {\ partial \ upvartheta b}} \ right) + \ frac {1} {{\ mathrm {rb}} ^ 2 {\ sin} ^ 2 \ upvartheta \ mathrm {b }} \ frac {\ partial ^ 2 {v} _ {\ mathrm { rb}}} {\ partial {\ upvarphi \ mathrm {b}} ^ 2} - \ frac {2 {v} _ {\ mathrm {rb}}} {{\ mathrm {rb}} ^ 2} - \ frac {2} {{\ mathrm {rb}} ^ 2 \ sin \ upvartheta \ mathrm {b}} \ frac {\ partial \ left ({v} _ {\ upvartheta \ mathrm {b}} \ mathrm {sin} \ upvartheta \ mathrm {b} \ right)} {\ mathrm {\ partial \ upvartheta b}} - \ frac {2} {{\ mathrm {rb}} ^ 2 \ mathrm {sin} \ upvartheta \ mathrm {b}} \ frac {\ partial {v} _ {\ upvarphi \ mathrm {b}}} {\ partial _ {\ upvarphi \ mathrm {b}}} \ right]} $$ (10)

Частицы имеют наноразмеры; таким образом, их радиусы будут очень малы, и для простоты уравнение. 10 представлена следующим образом:

$$ \ mathrm {d} \ upnu =\ left [\ frac {v _ {\ upvartheta \ mathrm {n}}} {\ mathrm {rn}} \ frac {\ partial {v} _ {\ mathrm {rn}} } {\ mathrm {\ partial \ upvartheta n}} + \ frac {v _ {\ upvarphi \ mathrm {n}}} {\ mathrm {rn} \ \ mathrm {sin} \ upvartheta \ mathrm {n}} \ frac { \ partial {v} _ {\ mathrm {rn}}} {\ mathrm {\ partial \ upvarphi n}} - \ frac {v _ {\ upvartheta \ mathrm {n}} ^ 2} {\ mathrm {rn}} - \ frac {v _ {\ upvarphi \ mathrm {n}} ^ 2} {\ mathrm {rn}} + \ frac {1} {\ rho} \ frac {\ partial p} {\ mathrm {\ partial rn}} \ right] / \ left [\ frac {1} {{\ mathrm {rn}} ^ 2} \ frac {\ partial} {\ mathrm {\ partial rn}} \ left ({\ mathrm {rn}} ^ 2 \ frac {\ partial {v} _ {\ mathrm {rn}}} {\ mathrm {\ partial rn}} \ right) + \ frac {1} {{\ mathrm {rn}} ^ 2 \ mathrm {sin} \ upvartheta \ mathrm {n}} \ frac {\ partial} {\ mathrm {\ partial \ upvartheta n}} \ left (\ mathrm {sin} \ upvartheta \ mathrm {n} \ frac {\ partial {\ mathrm {v}) } _ {\ mathrm {rn}}} {\ mathrm {\ partial \ upvartheta n}} \ right) + \ frac {1} {{\ mathrm {rn}} ^ 2 {\ sin} ^ 2 \ upvartheta \ mathrm {n}} \ frac {\ partial ^ 2 {\ mathrm {v}} _ {\ mathrm {rn}}} {\ partial {\ upvarphi \ mathrm {n}} ^ 2} - \ frac {2 {\ mathrm {v}} _ {\ mathrm {rn}}} {{\ math rm {rn}} ^ 2} - \ frac {2} {{\ mathrm {rn}} ^ 2 \ sin \ upvartheta \ mathrm {n}} \ frac {\ partial \ left ({\ mathrm {v}} _ {\ upvartheta \ mathrm {n}} \ mathrm {sin} \ upvartheta \ mathrm {n} \ right)} {\ mathrm {\ partial \ upvartheta n}} - \ frac {2} {{\ mathrm {rn}} ^ 2 \ mathrm {sin} \ upvartheta \ mathrm {n}} \ frac {\ partial {\ mathrm {v}} _ {\ upvarphi \ mathrm {n}}} {\ partial _ {\ upvarphi \ mathrm {n}} } \ right] =\ left [\ frac {{\ mathrm {v}} _ {\ upvartheta \ mathrm {a}}} {\ mathrm {ra}} \ frac {\ partial {\ mathrm {v}} _ { \ mathrm {ra}}} {\ mathrm {\ partial \ upvartheta a}} + \ frac {{\ mathrm {v}} _ {\ upvarphi \ mathrm {a}}} {\ mathrm {ra} \ \ mathrm { sin} \ upvartheta \ mathrm {a}} \ frac {\ partial {\ mathrm {v}} _ {\ mathrm {ra}}} {\ mathrm {\ partial \ upvarphi a}} - \ frac {{\ mathrm { v}} _ {\ upvartheta \ mathrm {a}} ^ 2} {\ mathrm {ra}} - \ frac {{\ mathrm {v}} _ {\ upvarphi \ mathrm {a}} ^ 2} {\ mathrm {ra}} + \ frac {1} {\ uprho} \ frac {\ mathrm {\ partial p}} {\ mathrm {\ partial ra}} \ right] / \ left [\ frac {1} {{\ mathrm {ra}} ^ 2} \ frac {\ partial} {\ mathrm {\ partial ra}} \ left ({\ mathrm {ra}} ^ 2 \ frac {\ partial {\ mathrm {v}} _ {\ mathrm {ra}}} {\ mathrm {\ partial ra}} \ rig ht) + \ frac {1} {{\ mathrm {ra}} ^ 2 \ mathrm {sin} \ upvartheta \ mathrm {a}} \ frac {\ partial} {\ mathrm {\ partial \ upvartheta a}} \ left (\ mathrm {sin} \ upvartheta \ mathrm {a} \ frac {\ partial {\ mathrm {v}} _ {\ mathrm {ra}}} {\ mathrm {\ partial \ upvartheta a}} \ right) + \ гидроразрыв {1} {{\ mathrm {ra}} ^ 2 {\ sin} ^ 2 \ upvartheta \ mathrm {a}} \ frac {\ partial ^ 2 {\ mathrm {v}} _ {\ mathrm {ra}} } {\ partial {\ upvarphi \ mathrm {a}} ^ 2} - \ frac {2 {\ mathrm {v}} _ {\ mathrm {ra}}} {{\ mathrm {ra}} ^ 2} - \ гидроразрыв {2} {{\ mathrm {ra}} ^ 2 \ sin \ upvartheta \ mathrm {a}} \ frac {\ partial \ left ({\ mathrm {v}} _ {\ upvartheta \ mathrm {a}} \ mathrm {sin} \ upvartheta \ mathrm {a} \ right)} {\ mathrm {\ partial \ upvartheta a}} - \ frac {2} {{\ mathrm {ra}} ^ 2 \ mathrm {sin} \ upvartheta \ mathrm {a}} \ frac {\ partial {v} _ {\ upvarphi \ mathrm {a}}} {\ partial _ {\ upvarphi \ mathrm {a}}} \ right] =\ left [\ frac {v _ {\ upvartheta \ mathrm {b}}} {\ mathrm {rb}} \ frac {\ partial {v} _ {\ mathrm {rb}}} {\ mathrm {\ partial \ upvartheta b}} + \ frac {v _ {\ upvarphi \ mathrm {b}}} {\ mathrm {rb} \ \ mathrm {sin} \ upvartheta \ mathrm {b}} \ frac {\ partial {v} _ {\ mathrm {rb}}} {\ mathrm {\ частичный \ upvarphi b}} - \ frac {v _ {\ upvartheta \ mathrm {b}} ^ 2} {\ mathrm {rb}} - \ frac {v _ {\ upvarphi \ mathrm {b}} ^ 2} {\ mathrm {rb }} + \ frac {1} {\ rho} \ frac {\ partial p} {\ mathrm {\ partial rb}} \ right] / \ left [\ frac {1} {{\ mathrm {rb}} ^ 2 } \ frac {\ partial} {\ mathrm {\ partial rb}} \ left ({\ mathrm {rb}} ^ 2 \ frac {\ partial {v} _ {\ mathrm {rb}}} {\ mathrm {\ частичный rb}} \ right) + \ frac {1} {{\ mathrm {rb}} ^ 2 \ mathrm {sin} \ upvartheta \ mathrm {b}} \ frac {\ partial} {\ mathrm {\ partial \ upvartheta b}} \ left (\ mathrm {sin} \ upvartheta \ mathrm {b} \ frac {\ partial {v} _ {\ mathrm {rb}}} {\ mathrm {\ partial \ upvartheta b}} \ right) + \ frac {1} {{\ mathrm {rb}} ^ 2 {\ sin} ^ 2 \ upvartheta \ mathrm {b}} \ frac {\ partial ^ 2 {v} _ {\ mathrm {rb}}} {\ частичное {\ upvarphi \ mathrm {b}} ^ 2} - \ frac {2 {v} _ {\ mathrm {rb}}} {{\ mathrm {rb}} ^ 2} - \ frac {2} {{\ mathrm {rb}} ^ 2 \ sin \ upvartheta \ mathrm {b}} \ frac {\ partial \ left ({v} _ {\ upvartheta \ mathrm {b}} \ mathrm {sin} \ upvartheta \ mathrm {b} \ right)} {\ mathrm {\ partial \ upvartheta b}} - \ frac {2} {{\ mathrm {rb}} ^ 2 \ mathrm {sin} \ upvartheta \ mathrm {b}} \ frac {\ partial { v} _ {\ upvarphi \ mathrm {b}}} {\ partial _ {\ upvarphi \ mathrm {b}}} \ right] $$ (11)

Уравнение 11 можно представить следующим образом:

$$ \ mathrm {d} \ upnu =\ mathrm {rn} \ left [{v} _ {\ upvartheta \ mathrm {n}} \ frac {\ partial {v} _ {\ mathrm {rn}}} {\ mathrm {\ partial \ upvartheta n}} + \ frac {v _ {\ upvarphi \ mathrm {n}}} {\ \ mathrm {sin} \ upvartheta \ mathrm {n}} \ frac {\ partial {v} _ {\ mathrm {rn}}} {\ mathrm {\ partial \ upvarphi n}} - {v} _ {\ upvartheta \ mathrm {n}} ^ 2- {v} _ {\ upvarphi \ mathrm {n}} ^ 2+ \ frac {\ mathrm {rn}} {\ rho} \ frac {\ partial p} {\ mathrm {\ partial rn}} \ right] / \ left [\ frac {\ partial} {\ mathrm {\ partial rn} } \ left ({\ mathrm {rn}} ^ 2 \ frac {\ partial {v} _ {\ mathrm {rn}}} {\ mathrm {\ partial rn}} \ right) + \ frac {1} {\ mathrm {sin} \ upvartheta \ mathrm {n}} \ frac {\ partial} {\ mathrm {\ partial \ upvartheta n}} \ left (\ mathrm {sin} \ upvartheta \ mathrm {n} \ frac {\ partial { v} _ {\ mathrm {rn}}} {\ mathrm {\ partial \ upvartheta n}} \ right) + \ frac {1} {\ sin ^ 2 \ upvartheta \ mathrm {n}} \ frac {\ partial ^ 2 {v} _ {\ mathrm {rn}}} {\ partial {\ upvarphi \ mathrm {n}} ^ 2} -2 {v} _ {\ mathrm {rn}} - \ frac {2} {\ sin \ upvartheta \ mathrm {n}} \ frac {\ partial \ left ({v} _ {\ upvartheta \ mathrm {n}} \ mathrm {sin} \ upvartheta \ mathrm {n} \ right)} {\ mathrm {\ номинал tial \ upvartheta n}} - \ frac {2} {\ mathrm {sin} \ upvartheta \ mathrm {n}} \ frac {\ partial {v} _ {\ upvarphi \ mathrm {n}}} {\ partial _ {\ upvarphi \ mathrm {n}}} \ right] =\ mathrm {ra} \ left [{v} _ {\ upvartheta \ mathrm {a}} \ frac {\ partial {v} _ {\ mathrm {ra}}} {\ mathrm {\ partial \ upvartheta a}} + \ frac {v _ {\ upvarphi \ mathrm {a}}} {\ \ mathrm {sin} \ upvartheta \ mathrm {a}} \ frac {\ partial {v} _ {\ mathrm {ra}}} {\ mathrm {\ partial \ upvarphi a}} - {v} _ {\ upvartheta \ mathrm {a}} ^ 2- {v} _ {\ upvarphi \ mathrm {a}} ^ 2+ \ frac {\ mathrm {ra}} {\ rho} \ frac {\ partial p} {\ mathrm {\ partial ra}} \ right] / \ left [\ frac {\ partial} {\ mathrm {\ partial} ra}} \ left ({\ mathrm {ra}} ^ 2 \ frac {\ partial {v} _ {\ mathrm {ra}}} {\ mathrm {\ partial ra}} \ right) + \ frac {1} {\ mathrm {sin} \ upvartheta \ mathrm {a}} \ frac {\ partial} {\ mathrm {\ partial \ upvartheta a}} \ left (\ mathrm {sin} \ upvartheta \ mathrm {a} \ frac {\ partial {v} _ {\ mathrm {ra}}} {\ mathrm {\ partial \ upvartheta a}} \ right) + \ frac {1} {\ sin ^ 2 \ upvartheta \ mathrm {a}} \ frac {\ partial ^ 2 {v} _ {\ mathrm {ra}}} {\ partial {\ upvarphi \ mathrm {a}} ^ 2} -2 {v} _ {\ mathrm {ra}} - \ frac {2} { \ грех \ upvartheta \ mathrm {a}} \ frac {\ partial \ left ({v} _ {\ upvartheta \ mathrm {a}} \ mathrm {sin} \ upvartheta \ mathrm {a} \ right)} {\ mathrm {\ partial \ upvartheta a}} - \ frac {2} {\ mathrm {sin} \ upvartheta \ mathrm {a}} \ frac {\ partial {v} _ {\ upvarphi \ mathrm {a}}} {\ partial _ {\ upvarphi \ mathrm {a}}} \ right] =\ mathrm {rb} \ left [{v} _ {\ upvartheta \ mathrm {b}} \ frac {\ partial {v} _ {\ mathrm {rb}}} {\ mathrm {\ partial \ upvartheta b}} + \ frac {v _ {\ upvarphi \ mathrm {b}}} {\ \ mathrm {sin} \ upvartheta \ mathrm {b}} \ frac {\ partial {v} _ {\ mathrm {rb}}} {\ mathrm {\ partial \ upvarphi b}} - {v} _ {\ upvartheta \ mathrm {b}} ^ 2- {v} _ {\ upvarphi \ mathrm {b}} ^ 2+ \ frac {\ mathrm {rb}} {\ rho} \ frac {\ partial p} {\ mathrm {\ partial rb}} \ right] / \ left [\ frac {\ partial} {\ mathrm {\ partial} rb}} \ left ({\ mathrm {rb}} ^ 2 \ frac {\ partial {v} _ {\ mathrm {rb}}} {\ mathrm {\ partial rb}} \ right) + \ frac {1} {\ mathrm {sin} \ upvartheta \ mathrm {b}} \ frac {\ partial} {\ mathrm {\ partial \ upvartheta b}} \ left (\ mathrm {sin} \ upvartheta \ mathrm {b} \ frac {\ partial {v} _ {\ mathrm {rb}}} {\ mathrm {\ partial \ upvartheta b}} \ right) + \ frac {1} {\ si n ^ 2 \ upvartheta \ mathrm {b}} \ frac {\ partial ^ 2 {v} _ {\ mathrm {rb}}} {\ partial {\ upvarphi \ mathrm {b}} ^ 2} -2 {v} _ {\ mathrm {rb}} - \ frac {2} {\ sin \ upvartheta \ mathrm {b}} \ frac {\ partial \ left ({v} _ {\ upvartheta \ mathrm {b}} \ mathrm {sin } \ upvartheta \ mathrm {b} \ right)} {\ mathrm {\ partial \ upvartheta b}} - \ frac {2} {\ mathrm {sin} \ upvartheta \ mathrm {b}} \ frac {\ partial {v } _ {\ upvarphi \ mathrm {b}}} {\ partial _ {\ upvarphi \ mathrm {b}}} \ right] $$ (12)

Существует прямая зависимость между радиусом наночастиц и вязкостью лимфы из-за рака. Если лимфа становится слишком статичной и вязкой, она не может правильно выполнять свою функцию - циркуляцию, очистку от токсинов и помощь в борьбе с раком. Если размер наночастиц меньше, лимфатические раковые клетки легко убить. Чтобы описать перенос общего количества наночастиц соединения, мы используем уравнение неразрывности и принимаем три наночастицы твердых тел A, B и N следующим образом:

$$ \ frac {1} {{\ mathrm {ra}} ^ 2} \ frac {\ partial} {\ mathrm {\ partial ra}} \ left ({\ mathrm {ra}} ^ 2 {v} _ { \ mathrm {ra}} \ right) + \ frac {1} {\ mathrm {ra} \ \ mathrm {sin} \ upvartheta \ mathrm {a}} \ frac {\ partial} {\ mathrm {\ partial \ upvartheta a }} \ left (\ sin {\ upvartheta \ mathrm {v}} _ {\ upvartheta \ mathrm {a}} \ right) + \ frac {1} {\ mathrm {ra} \ \ mathrm {sin} \ upvartheta \ mathrm {a}} \ frac {\ partial {v} _ {\ upvarphi \ mathrm {a}}} {\ mathrm {\ partial \ upvarphi a}} + \ frac {1} {{\ mathrm {rb}} ^ 2} \ frac {\ partial} {\ mathrm {\ partial rb}} \ left ({\ mathrm {rb}} ^ 2 {v} _ {\ mathrm {rb}} \ right) + \ frac {1} { \ mathrm {rb} \ \ mathrm {sin} \ upvartheta \ mathrm {b}} \ frac {\ partial} {\ mathrm {\ partial \ upvartheta b}} \ left (\ sin {\ upvartheta v} _ {\ upvartheta \ mathrm {b}} \ right) + \ frac {1} {\ mathrm {rb} \ \ mathrm {sin} \ upvartheta \ mathrm {b}} \ frac {\ partial {v} _ {\ upvarphi \ mathrm { b}}} {\ mathrm {\ partial \ upvarphi b}} + \ frac {1} {{\ mathrm {rn}} ^ 2} \ frac {\ partial} {\ mathrm {\ partial rn}} \ left ( {\ mathrm {rn}} ^ 2 {v} _ {\ mathrm {rn}} \ right) + \ frac {1} {\ mathrm {rn} \ \ mathrm {sin} \ upvartheta \ mathrm {n}} \ гидроразрыв {\ parti al} {\ mathrm {\ partial \ upvartheta n}} \ left (\ sin {\ upvartheta v} _ {\ upvartheta \ mathrm {n}} \ right) + \ frac {1} {\ mathrm {rn} \ \ mathrm {sin} \ upvartheta \ mathrm {n}} \ frac {\ partial {v} _ {\ upvarphi \ mathrm {n}}} {\ mathrm {\ partial \ upvarphi n}} =0 $$ (13)

Вязкость динамической жидкости может быть определена по следующему уравнению [23]:

$$ \ mathrm {Vs} =\ frac {2} {9} \ frac {r ^ 2g \ \ left (\ uprho \ mathrm {p} - \ uprho \ mathrm {f} \ right)} {\ mathrm {dv }} $$ (14)

where Vs is the particles’ settling velocity (m/s), r is the Stokes radius of the particle (m), g is the gravitational acceleration (m/s² ), ρp is the density of the particles (kg/m³ ), ρf is the density of the fluid (kg/m³ ), and dv is the (dynamic) fluid viscosity (Pa·s). The lymph fluid is slightly heavier than water (lymph density = 1019 kg/m³ , water density = 998.28 kg/m³ at 20 °C). As a reference value, we consider the dynamic viscosity of the water to be 1.002 × 10^–3 kg m^–1 s^–1 ).

Dynamic viscosity is the measurement of the fluid’s internal resistance to flow, while kinematic viscosity refers to the ratio of dynamic viscosity to density. The effect of all the nanoparticles on the fluid viscosity is represented as follows:

$$ \mathrm{dv}=\frac{2\mathrm{g}}{9}\left[\frac{{\mathrm{ra}}^2\left(\uprho \mathrm{a}-\uprho \mathrm{f}\right)}{\mathrm{vsa}}+\frac{{\mathrm{rb}}^2\left(\uprho \mathrm{b}-\uprho \mathrm{f}\right)}{\mathrm{vsb}}+\frac{{\mathrm{rn}}^2\left(\uprho \mathrm{n}-\uprho \mathrm{f}\right)}{\mathrm{vn}}\right] $$ (15)

By comparing Eq. 12 and Eq. 15, the following equation could be emerged:

$$ \left|\frac{2\mathrm{g}}{9}\left[\frac{{\mathrm{ra}}^2\left(\uprho \mathrm{a}-\uprho \mathrm{f}\right)}{\mathrm{vsa}}+\frac{{\mathrm{rb}}^2\left(\uprho \mathrm{b}-\uprho \mathrm{f}\right)}{\mathrm{vsb}}+\frac{{\mathrm{rn}}^2\left(\uprho \mathrm{n}-\uprho \mathrm{f}\right)}{\mathrm{vn}}\right]\right|=\mathrm{rn}\left[{v}_{\upvartheta \mathrm{n}}\frac{\partial {v}_{\mathrm{rn}}}{\mathrm{\partial \upvartheta n}}+\frac{v_{\upvarphi \mathrm{n}}}{\ \mathrm{sin}\upvartheta \mathrm{n}}\frac{\partial {v}_{\mathrm{rn}}}{\mathrm{\partial \upvarphi n}}-{v}_{\upvartheta \mathrm{n}}^2-{v}_{\upvarphi \mathrm{n}}^2+\frac{\mathrm{rn}}{\uprho \mathrm{f}}\frac{\mathrm{\partial p}}{\mathrm{\partial rn}}\right]/\left[\frac{\partial }{\mathrm{\partial rn}}\left({\mathrm{rn}}^2\frac{\partial {v}_{\mathrm{rn}}}{\mathrm{\partial rn}}\right)+\frac{1}{\mathrm{sin}\upvartheta \mathrm{n}}\frac{\partial }{\mathrm{\partial \upvartheta n}}\left(\mathrm{sin}\upvartheta \mathrm{n}\frac{\partial {v}_{\mathrm{rn}}}{\mathrm{\partial \upvartheta n}}\right)+\frac{1}{\sin^2\upvartheta \mathrm{n}}\frac{\partial^2{v}_{\mathrm{rn}}}{\partial {\upvarphi \mathrm{n}}^2}-2{v}_{\mathrm{rn}}-\frac{2}{\sin \upvartheta \mathrm{n}}\frac{\partial \left({v}_{\upvartheta \mathrm{n}}\mathrm{sin}\upvartheta \mathrm{n}\right)}{\mathrm{\partial \upvartheta n}}-\frac{2}{\mathrm{sin}\upvartheta \mathrm{n}}\frac{\partial {v}_{\upvarphi \mathrm{n}}}{\partial_{\upvarphi \mathrm{n}}}\right]=\mathrm{ra}\left[{v}_{\upvartheta \mathrm{a}}\frac{\partial {v}_{\mathrm{ra}}}{\mathrm{\partial \upvartheta a}}+\frac{v_{\upvarphi \mathrm{a}}}{\ \mathrm{sin}\upvartheta \mathrm{a}}\frac{\partial {v}_{\mathrm{ra}}}{\mathrm{\partial \upvarphi a}}-{v}_{\upvartheta \mathrm{a}}^2-{v}_{\upvarphi \mathrm{a}}^2+\frac{\mathrm{ra}}{\uprho \mathrm{f}}\frac{\partial p}{\mathrm{\partial ra}}\right]/\left[\frac{\partial }{\mathrm{\partial ra}}\left({\mathrm{ra}}^2\frac{\partial {v}_{\mathrm{ra}}}{\mathrm{\partial ra}}\right)+\frac{1}{\mathrm{sin}\upvartheta \mathrm{a}}\frac{\partial }{\mathrm{\partial \upvartheta a}}\left(\mathrm{sin}\upvartheta \mathrm{a}\frac{\partial {v}_{\mathrm{ra}}}{\mathrm{\partial \upvartheta a}}\right)+\frac{1}{\sin^2\upvartheta \mathrm{a}}\frac{\partial^2{v}_{\mathrm{ra}}}{\partial {\upvarphi \mathrm{a}}^2}-2{v}_{\mathrm{ra}}-\frac{2}{\sin \upvartheta \mathrm{a}}\frac{\partial \left({v}_{\upvartheta \mathrm{a}}\mathrm{sin}\upvartheta \mathrm{a}\right)}{\mathrm{\partial \upvartheta a}}-\frac{2}{\mathrm{sin}\upvartheta \mathrm{a}}\frac{\partial {v}_{\upvarphi \mathrm{a}}}{\partial_{\upvarphi \mathrm{a}}}\right]=\mathrm{rb}\left[{v}_{\upvartheta \mathrm{b}}\frac{\partial {v}_{\mathrm{rb}}}{\mathrm{\partial \upvartheta b}}+\frac{v_{\upvarphi \mathrm{b}}}{\ \mathrm{sin}\upvartheta \mathrm{b}}\frac{\partial {v}_{\mathrm{rb}}}{\mathrm{\partial \upvarphi b}}-{v}_{\upvartheta \mathrm{b}}^2-{v}_{\upvarphi \mathrm{b}}^2+\frac{\mathrm{rb}}{\uprho \mathrm{f}}\frac{\partial p}{\mathrm{\partial rb}}\right]/\left[\frac{\partial }{\mathrm{\partial rb}}\left({\mathrm{rb}}^2\frac{\partial {v}_{\mathrm{rb}}}{\mathrm{\partial rb}}\right)+\frac{1}{\mathrm{sin}\upvartheta \mathrm{b}}\frac{\partial }{\mathrm{\partial \upvartheta b}}\left(\mathrm{sin}\upvartheta \mathrm{b}\frac{\partial {v}_{\mathrm{rb}}}{\mathrm{\partial \upvartheta b}}\right)+\frac{1}{\sin^2\upvartheta \mathrm{b}}\frac{\partial^2{v}_{\mathrm{rb}}}{\partial {\upvarphi \mathrm{b}}^2}-2{v}_{\mathrm{rb}}-\frac{2}{\sin \upvartheta \mathrm{b}}\frac{\partial \left({v}_{\upvartheta \mathrm{b}}\mathrm{sin}\upvartheta \mathrm{b}\right)}{\mathrm{\partial \upvartheta b}}-\frac{2}{\mathrm{sin}\upvartheta \mathrm{b}}\frac{\partial {v}_{\upvarphi \mathrm{b}}}{\partial_{\upvarphi \mathrm{b}}}\right] $$ (16)

Equation 16 depicts the relationship between the density of the lymph fluid, the density of the nanoparticles of the compound drug system, and the radius of the nanoparticles. There is a positive correlation between the density of the lymph fluid and the density of the nanoparticles. The smaller the density and radius of nanoparticles, the lesser the density of the fluid will be. As established earlier, the decrease in the density of the lymph fluid leads to its inability to reproduce and reduce the ferocity of the disease. It can, therefore, be concluded that the tumor can be cured by minimizing the size of nanoparticles. These particles can reach in the range of up to 0.1 nm (i.e., Angstrom or picometer range). The particles of this size can act as the nucleus of drug delivery in this drug system. Equation 16 shows that radii of the nanoparticles in the proposed drug system are related to the effectiveness of the delivery system. Much lower sized nanoparticles can reduce the density of lymph fluid and the spread of the disease.

Nanoparticles with Nanoantennas

This study used the nanoparticle described in an earlier report [22] as an emissary with a nano-microcontroller. In the system, the proposed transmission distance is very small and compatible with the composition of nanoparticles. Thus, the middle gap can be neglected in mid-distance and is symbolized by C _d . Further, R _а и X _а are the real part and the imaginary part of the anaerobic impedance. After neglecting the load of the intercellular space between the nanoparticles and the nano-microcontroller, R _а и X _а can be calculated as follows [22]:

$$ {R}_a=\frac{r_{a0}}{1+{C}_d{w}_a\left(2{x}_{a0}+{C}_d\left({r_{a0}}^2+{x_{a0}}^2\right){w}_a\right)} $$ (17) $$ {X}_a=\frac{x_0-{C}_d\left({r_{a0}}^2+{x_{a0}}^2\right){w}_a}{1+{C}_d{w}_a\left(2{x}_{a0}+{C}_d\left({r_{a0}}^2+{x_{a0}}^2\right){w}_a\right)} $$ (18)

Thus, the load resistance value of nanotubes can be predicted as in the following equation:

$$ {r}_l=\frac{g^2R}{g^2-2 gSX{\varepsilon}_L\omega +{S}^2\left({R}^2+{X}^2\right){\varepsilon_L}^2{\omega}^2} $$ (19)

где ε _L is the permittivity of the loading material, g is the size of the gap, and S is the effective cross-section area of the gap. In order to simplify the equation, the value of g ² can be neglected as it is too low and the final equation can be rewritten as follows:

$$ {r}_l=\frac{g^2R}{-2 gSX{\varepsilon}_L\omega +{S}^2\left({R}^2+{X}^2\right){\varepsilon_L}^2{\omega}^2} $$ (20)

Then,

$$ {r}_l=\frac{g^2R}{S{\varepsilon}_L\omega \left(-2 gX+S\left({R}^2+{X}^2\right){\varepsilon}_L\omega \right)} $$ (21)

The optical nano-photo concept can be used as an effective tool for interpreting and predicting these effects to design and improve nanoscale parameters and increase the nano-sensitivity to serve better as a single molecular sensor. Nanoantenna may provide optimal performance in terms of sensitivity, efficiency, and bandwidth in the process. The next section presents the concept of searching the cancerous lymph nodes using compressive binary search algorithm.

Searching for the Target Lymphatic Nodes Using Compressive Binary Search

In order for nanoparticles to reach the cancerous cells in a fast and efficient manner, we applied compressive binary search by the nano-microcontroller. The guided nanoparticles follow a specific path to quickly reach the target. This movement is based on the information obtained from the “exploratory nanoparticles.” Assume that the target lymph node, Tf, has exactly one nonzero entry, where the location of the lymph node is unknown. The algorithm divides mt measurements into a total of St stages, where St refers to the stages of the lymph nodes. The measurements are more than one for all the stages of the lymph nodes, which is necessary for the algorithm to be executed until completion. Based on this measurement, the algorithm decides between going left or right, until the nanoparticles reach the target, the cancerous lymph node.

Результаты и обсуждение

In order to analyze the proposed design, the nanoparticles were applied to the following five types of materials:silicone, lithium, lung, helium, and hydrogen. The materials were chosen because of their low density. The lung nanoparticles were samples from nano-sized lung nodules. They appear encircling with white shadows in a chest X-ray or computerized tomography scan taken from the lung of the person and required to be undamaged. The proposed idea is based on the analytical model, which indicates that the smaller the density of nanoparticles, the smaller the dynamic viscosity will be. This will result in a decrease in fluid viscosity. It is shown that the types of materials and the density of each particle will affect settling velocity of nanoparticles at entry into the lymphatic fluid and the density of the lymphatic fluid. We considered the following parameters:acceleration of gravity (g ) = 9.80665, particle diameter (d ) = 10 A, initial density of lymph fluid (ρf) = 998.28, and dynamic viscosity = 0.0010 kg m^–1 s^–1 [24]. These parameters were selected by the assumption that the viscosity of the lymphatic fluid is very similar to the viscosity of the water and the very small difference does not affect the results of the model. Figure 4 illustrates the density of nanoparticles for five selected materials for application in the proposed analytical model. Figure 5 shows the settling velocity for each particle. Figure 6 shows the effect of the settling velocity of nanoparticles on altering the lymphocyte density of cancer cells. The results shown in Fig. 6 show that the settling velocity of the particles carries a negative value. This indicates that the nanoparticle after entering in the lymphatic fluid rapidly moves in the opposite direction toward their entry into the lymphatic fluid. In general, any object that moves in the negative direction has a negative velocity. This movement of the particle leads to reduced viscosity of the lymphatic fluid.

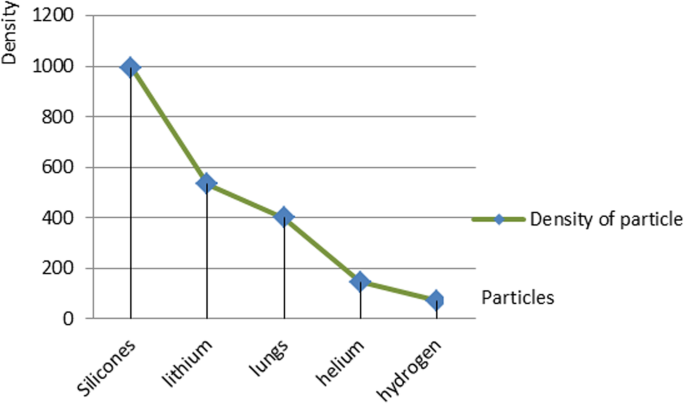
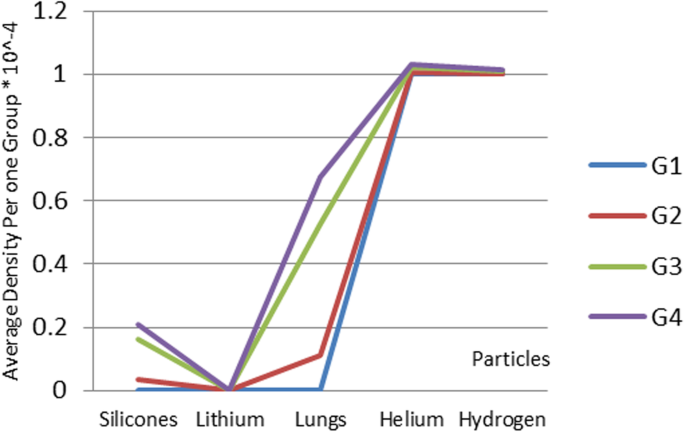
Density of nanoparticles for the five selected materials

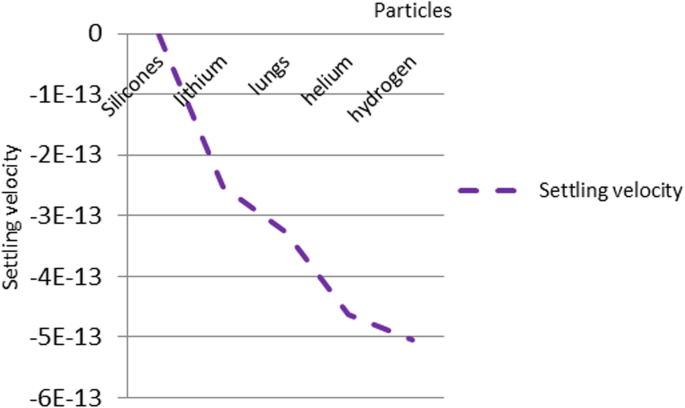
The settling velocity data for each particle

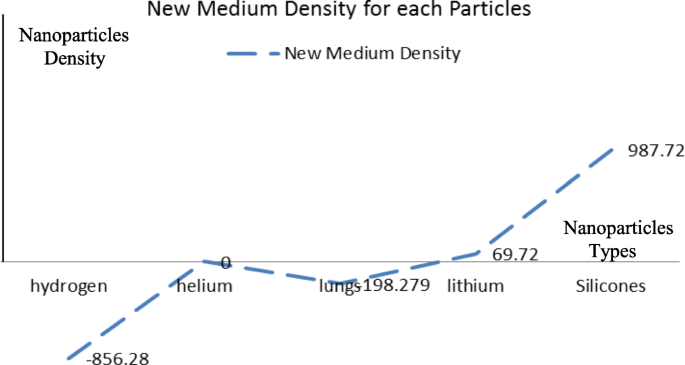
The effect of the settling velocity of nanoparticles on changing the lymphocyte density of cancer cells

Silicone nanoparticles showed the settling velocity of approximately − 2.87 × 10–15 m/s. This resulted in a decrease in viscosity of the lymphatic fluid to 987.72 kg/m³ for the initial density 998.28 kg/m³ . The density is continuously reduced to a point where hydrogen produces extremely spectacular results, i.e., the complete collapse of lymphatic fluid resistance. The density of the lymphatic fluid − 856.28 kg/m³ with the negative sign indicated that there was no resistance from the lymphatic fluid to the flow of the nanoparticles, resulting in the complete collapse of the liquid fluid. Both the hydrogen and helium particles have a significant impact on the liquid viscosity due to the low density of the particles. Hence, it is important to use a drug system consisting of a group of nanoparticles for low-density materials. Figure 7 shows the relationship between the diameters of lung nanoparticles and the number of nanoparticles in one group. The figure shows that the higher the diameter of nanoparticles, the fewer their number in a group. This is clearly shown at the highest value of the nanoparticle diameter of 1000 nm, where the number of molecules in a group is 20 molecules. Figure 8 shows the relationship between the diameters of lithium nanoparticles and the number of nanoparticles in one group. This figure demonstrates the inverse relationship between the radius of nanoparticles and the number of molecules in a group where lithium particle diameters are significantly lower than the lung nanoparticles, where the number of nanoparticles in Fig. 7 is relatively low compared to the lithium particles as shown in Fig. 8. And the multicolor balls in both figures refer to different ranges of nanoparticle radii for each group, where each group contains a number of nanoparticles with different sizes. The best results can be obtained when hydrogen and helium particles are increased from other substances. A mixture of different materials should be used so that the properties of these substances can be used in the treatment process as well as to reduce viscosity. Figure 9 illustrates the different sets of materials proposed to have the mean highest density of both hydrogen and helium materials. Figure 10 shows the average mass of a nanoparticle in a group. It can be seen that the mass of both hydrogen and helium is the highest compared to the mass of particles of other substances. Figure 11 illustrates the relationship between the diameters of the nanoparticles and the width of its group or class. It is important to note that these results will open up a new area to reduce the resistance of the lymphatic fluid in tumors. This can be achieved using hydrogen nanoparticles of a size in the range of Angstrom. In addition to hydrogen nanoparticles, there may also exist a number of other substances in the same size. Figure 12 illustrates the standard deviation of a number of coefficients for both lung and lithium nanoparticles. These coefficients are limited to fractions of nanoparticles in a single group as well as their number in addition to the diameters of these nanoparticles. It is clear that the group fractions have the less value of the standard deviation. Hence, most of the fractions in the computational processes are around the mean of these values. Figure 13 shows the standard deviation of the mass for particles of silicones, lithium, lungs, helium, and hydrogen in one group. It is clear that the particles of the lung have the largest standard deviation and the lithium has the minimum value.

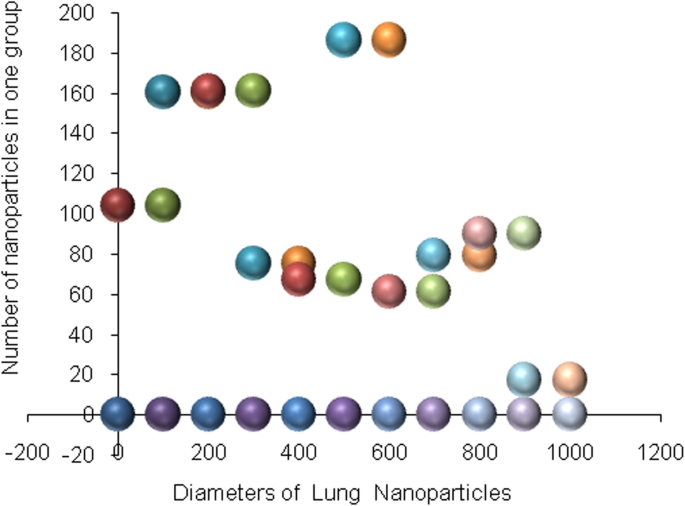
Group of nanoparticles in the lung cells and their number in one of the proposed groups

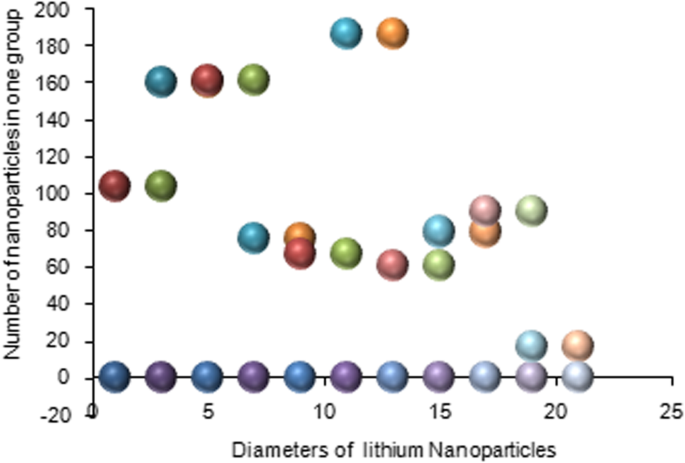
Group of nanoparticles in the lithium cells and their number in one of the proposed groups

Different sets of materials proposed to have the mean highest density of both hydrogen and helium materials

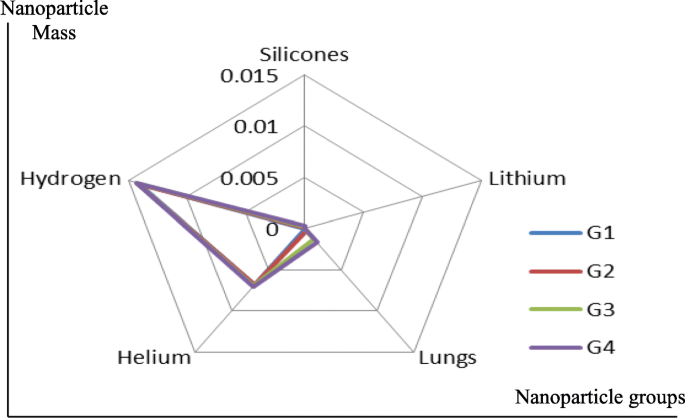
Average mass of a nanoparticle in a group

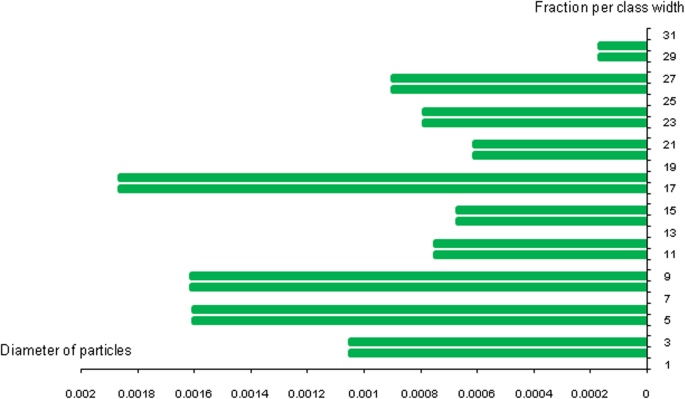
Diameters of the nanoparticles related to the group width

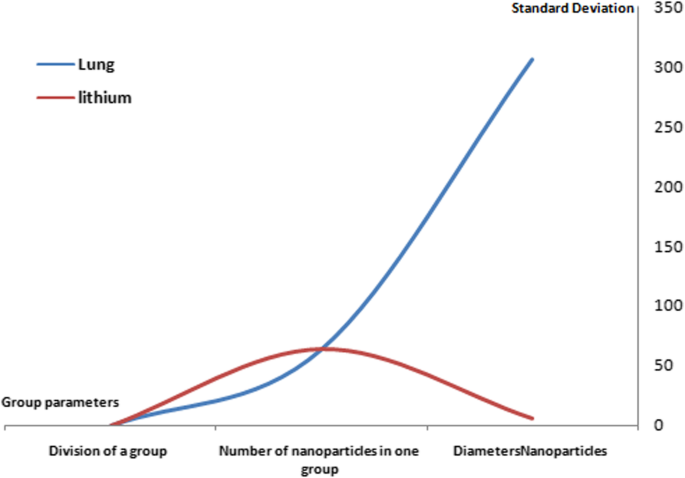
The standard deviation of lung and lithium nanoparticles coefficients

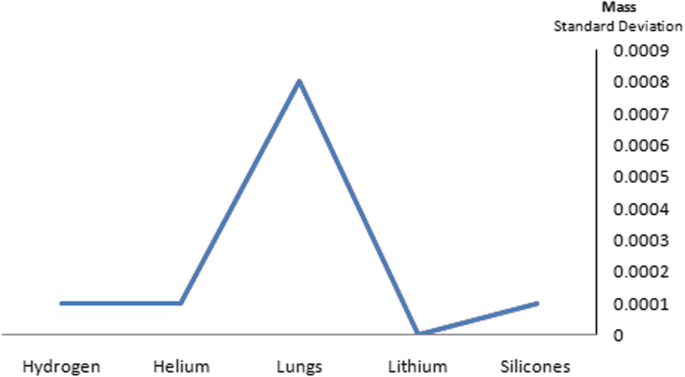
The standard deviation of the mass for particles of silicones, lithium, lungs, helium, and hydrogen in one group

Methods

The aim of this study was to establish a nano-drug delivery system capable of delivering the drugs effectively to the cancer cells. The following methodology was used to deliver nanoparticles:

i)
Low-density nanoparticles

This study proposed the theoretical approach of nanoparticles as a low-density drug. This depends on the density and the settling velocity of the nanoparticles, as these nanoparticles can overcome the resistance of the lymphatic fluid.

ii)
Preparation of anaerobic nanoparticles

This study uses the idea of nanoparticles possessing an antenna through which a connection can be made between nanoparticles and nano-controller. The transmission distance was assumed to be too small to match the composition of nanoparticles and also to fit the actual distance between them.

iii)
Nano-controller design

Its function is to deliver the nanoparticle drug to cancer cells. Its role is to send signals to the nanoparticles and coordinate their actions and direct them to the lymphatic fluid of tumors.

iv)
Searching for the target lymphatic nodes

The lymphatic nodes are searched using compressive binary search algorithm. This algorithm is characterized by high-speed search, which makes nanoparticles more accessible to infected cells than the conventional methods. The primary supervisor behind the performance of the nanoparticles is the nano-controller. It directs nanoparticles to the infected cells by following this algorithm to ensure that an appropriate number of molecules are in proportional density to the lymphatic fluid.

Заключение

There have been various studies managing the treatment of malignant growth utilizing nanoparticles. The lymphatic liquid in tumors plays a substantial role in the obstruction of medication to the cancer cells. We developed an intelligent drug delivery system containing a consortium of nanoparticles. The proposed design demonstrates that small nanoparticles result in low density of the fluid. The results indicated that hydrogen particles are most efficient in reducing resistance toward lymphatic liquid owing to their smaller size. Furthermore, the design involves an anaerobic nano-controller that can determine the state and area of the particles. This technique conveys the medication to the infected cell more effectively.

Доступность данных и материалов

The datasets supporting the results of this article are included within the article.

Сокращения

LN:: Lipid nanoparticles
NLC:: Nanostructured lipid carriers
PN:: Polymeric nanoparticles
SLNs:: Solid lipid nanoparticles

Приготовление и характеристика микронановолокон PAN / PS, загруженных AMT / Co (acac) 3, с большими сквозными порами Зависимость электронных и оптических свойств многослоев MoS2 от межслоевой связи и сингулярности Ван Хова

Наноматериалы