Двухэтапная методология изучения влияния агрегации / агломерации наночастиц на модуль Юнга полимерных нанокомпозитов

Фон

В последние годы многие исследователи сосредоточились на полимерных нанокомпозитах, чтобы определить эффективные параметры во взаимосвязи между обработкой, структурой и свойствами и оптимизировать общую производительность, измеряемую механическими, термическими, физическими и барьерными свойствами [1,2,3,4 ]. Низкое содержание наночастиц в полимерных нанокомпозитах обеспечивает большую межфазную поверхность, высокий модуль упругости, малый вес и недорогие продукты, которые чрезвычайно привлекательны в композитной промышленности. Соответственно, применение наночастиц - простой, эффективный и экономичный способ улучшить характеристики полимерных матриц. Влияние многих материалов и параметров обработки на свойства полимерных нанокомпозитов, содержащих силикатные слои (наноглина), углеродные нанотрубки (УНТ) и неорганические наполнители, такие как диоксид кремния (SiO ₂ ) и карбонат кальция (CaCO ₃ ) были исследованы [5,6,7,8].

Размер и качество дисперсии / распределения наночастиц в полимерной матрице изменяют общие свойства полимерных нанокомпозитов. Наночастицы имеют тенденцию к агрегированию и агломерации из-за притяжения между наночастицами, такого как силы Ван-дер-Ваальса и химические связи [9], или сильного уменьшения разделения поверхностей по мере уменьшения размера наполнителя [10]. Следовательно, наночастицы трудно диспергировать в полимерных матрицах в наномасштабе. И агрегация, и агломерация представляют собой сборки наночастиц, где агломерация включает прочные и плотные колонии частиц, но агломерация включает слабо связанные частицы, которые могут быть разрушены механическими силами. Агломерация / агрегация очевидна при высоком содержании наполнителя, что ухудшает наноразмерность наполнителя и вызывает множество дефектов и концентраций напряжений в нанокомпозитах [11,12,13]. Агломерация / агрегация также уменьшает площадь поверхности раздела между полимерной матрицей и наночастицами, что снижает механическое участие полимерных цепей в наночастицах и устраняет эффект жесткости. Наши недавние результаты [14, 15] и исследование Ji et al. [16] о механических свойствах показали, что любая агломерация / агломерация серьезно нарушает эффект придания жесткости наночастицам в полимерных нанокомпозитах.

Помимо экспериментальной характеристики нанокомпозитов, теоретические исследования, позволяющие количественно оценить зависимость механического поведения от свойств составляющих фаз и геометрической морфологии наночастиц, поставили перед недавними исследованиями привлекательные задачи. Теоретические исследования могут помочь уточнить экспериментальные результаты и облегчить оптимальный синтез многообещающих нанокомпозитов. Наночастицы в нанокомпозитах вносят беспорядок в прилегающую матрицу, что приводит к образованию межфазных зон, окружающих наполнитель, которые проявляют свойства, отличные от объемной матрицы и наночастиц [17,18,19]. Теоретические исследования межфазных свойств показали привлекательные результаты, оправдывающие использование наночастиц в полимерных нанокомпозитах [20,21,22].

Влияние агрегации / агломерации на механические характеристики нанокомпозитов исследовалось в предыдущих работах [11, 14, 23, 24]. В этих исследованиях обычно рассматривалась агрегация / агломерация крупными частицами. В последнее время для изучения свойств нанокомпозита использовались методы многомасштабного моделирования [25,26,27]. В данной статье предлагается двухэтапный метод для изучения роли агрегации / агломерации наночастиц в модуле Юнга полимерных нанокомпозитов, предполагая долю фазы агрегации / агломерации в нанокомпозите и долю наночастиц в агрегатах / агломератах. В связи с этим для выражения модуля Юнга нанокомпозитов применяются две микромеханические модели Пола и Максвелла. Для оценки прогнозов представлены многочисленные экспериментальные данные. Кроме того, изучается влияние параметров агломерации / агломерации на модуль Юнга нанокомпозитов.

Методы

Когда фракция наноразмерных частиц агрегируется / агломерируется, в нанокомпозите проявляется неравномерное распределение наночастиц. В результате можно предположить, что некоторые наночастицы находятся в сферических областях в матрице как фаза агрегации / агломерации, а другие равномерно диспергированы в полимерной матрице, как показано на рис. 1. Соответственно, нанонаполнитель показывает две части с разным армированием, которое может быть В расчетах рассматривались две разные фазы:агломерация / агломерация и эффективная матричная фаза, демонстрирующая области внутри и снаружи сфер, соответственно (рис. 1).

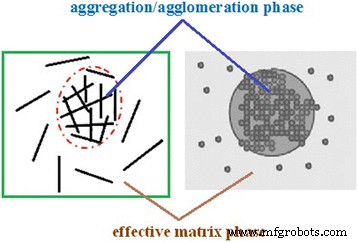
Схематическое изображение агломерации / агломерации и эффективных матричных фаз в полимерных нанокомпозитах, содержащих слоистые и сферические наночастицы

Для уровня агломерации / агломерации наночастиц в полимерном нанокомпозите предлагаются следующие два параметра:

где « V _agg »И« V ”Обозначают общие объемы фазы агломерации / агломерации и нанокомпозита, соответственно. Кроме того, « V _f ^agg »И« V _f ”Показывают объемы наночастиц в фазе агрегации / агломерации и нанокомпозите в целом, соответственно. Объемная доля наночастиц, включенных в фазу агрегации / агломерации, представлена ​​следующим образом:

где « ϕ _f ”- объемная доля нанонаполнителя в нанокомпозитах. Кроме того, объемная доля хорошо диспергированных наночастиц, включенных в фазу эффективной матрицы (вне фазы агрегации / агломерации), рассчитывается следующим образом:

В этом исследовании используется двухэтапная методология, основанная на микромеханических моделях, для определения параметров агрегации / агломерации ( z и y ) в полимерных нанокомпозитах по модулю Юнга. Во-первых, модуль агломерации / агломерации и эффективная матрица фаз рассчитываются по модели Пола. Во-вторых, предполагается, что фаза агломерации / агломерации представляет собой сферические включения в эффективной матрице, а модуль Юнга нанокомпозита рассчитывается с помощью модели Максвелла для композита, содержащего дисперсные частицы.

Пол [28] предложил модель, которая предполагает макроскопически однородное напряжение в двух компонентах композита, как:

где « E _м »И« E _f ”- модули Юнга полимерной матрицы и фазы наполнителя соответственно. На первом этапе модуль агрегации / агломерации ( E _agg ) и эффективная матрица ( E _mat ) фазы рассчитываются по модели Пола путем замены « ϕ _f »С« \ ({\ phi} _f ^ {agg} \) »и« \ ({\ phi} _f ^ {mat} \) »как:

Кроме того, модель Максвелла [29] для композитов, содержащих дисперсный наполнитель, задается следующим образом:

На втором этапе модель Максвелла применяется для расчета модуля в композите, содержащем эффективную матрицу (матрицу и хорошо диспергированные наночастицы) и фазы агрегации / агломерации путем замены « ϕ _f »С« z »(См. Уравнение 1),« E _f ”С модулем фазы агломерации / агломерации ( E _agg ) и « E _м ”С модулем эффективной матрицы ( E _mat ) как:

который коррелирует модуль Юнга нанокомпозитов с модулями агрегатов / агломератов и эффективной матрицы, а также с параметром «z». Когда « E _agg »И« E _mat ”Из Ур. 7 и 8 вводятся в последние уравнения, модуль нанокомпозитов выражается с использованием концентрации наполнителя, модуля наполнителя, модуля матрицы и « z »И« y »Параметры. Зависимость модуля от этих параметров является разумной, поскольку свойства полимера и наночастиц, а также степень агломерации / агломерации наполнителя определяют модуль упругости нанокомпозитов. В настоящей методологии y > z имеет смысл, потому что \ ({VV} _f ^ {\ mathrm {agg}}> {V} _f {V} _ {\ mathrm {agg}} \).

Результаты и обсуждение

Предлагаемый метод применяется для оценки агломерации / агломерации наночастиц в нескольких образцах из предыдущих исследований, включая ПВХ / CaCO ₃ [30], PCL / наноглина [31], ABS / наноглина [32], PLA / наноглина [33], PET / MWCNT [34] и полиимид / MWCNT [35]. На рисунке 2 показаны экспериментальные результаты модуля Юнга, а также прогнозы двухэтапного метода. Расчеты правильно соответствуют экспериментальным данным при различных концентрациях нанонаполнителя, что свидетельствует о правильности предложенного метода. Однако наибольшее согласие между экспериментальными и теоретическими данными достигается, когда агрегация / агломерация наночастиц предполагается соответствующими уровнями « z »И« y »Параметры. Самые высокие прогнозы « z »И« y »Параметры рассчитываются как z =0,2 и y =0,95 для ПВХ / CaCO ₃ нанокомпозит. Кроме того, ( z , y ) значения (0,3, 0,75), (0,1, 0,99) и (0,35, 0,7) получены для образцов PCL / наноглина, PLA / наноглина и PET / MWCNT соответственно. Кроме того, ( z , y ) уровни (0,2, 0,93) и (0,15, 0,9) рассчитаны для нанокомпозитов ПЭТ / MWCNT и полиимид / MWCNT соответственно. Эти уровни « z »И« y ”Параметры демонстрируют образование агрегированных / агломерированных наночастиц в указанных нанокомпозитах. Небольшое улучшение модуля в этих образцах подтверждает слабую дисперсность и высокий уровень накопления наночастиц в полимерных матрицах. Например, добавление 7,5 мас.% CaCO ₃ для ПВХ только увеличивает модуль упругости чистого ПВХ (1,13 ГПа) до 1,3 ГПа. Кроме того, включение 10 мас.% Наноглины в PCL только улучшает модуль упругости чистого PCL с 0,22 до 0,37 ГПа. Однако наночастицы демонстрируют высокий модуль упругости по сравнению с полимерными матрицами. Модуль Юнга CaCO ₃ , наноглина и MWCNT составили 26, 180 и 1000 ГПа [36] соответственно, в то время как модуль Юнга настоящих полимерных матриц едва достигает 2,5 ГПа. В результате агрегированные / агломерированные наночастицы значительно уменьшают модуль упругости в нанокомпозитах, и настоящая методология предлагает приемлемые данные для агломерации / агломерации наночастиц в полимерных нанокомпозитах.

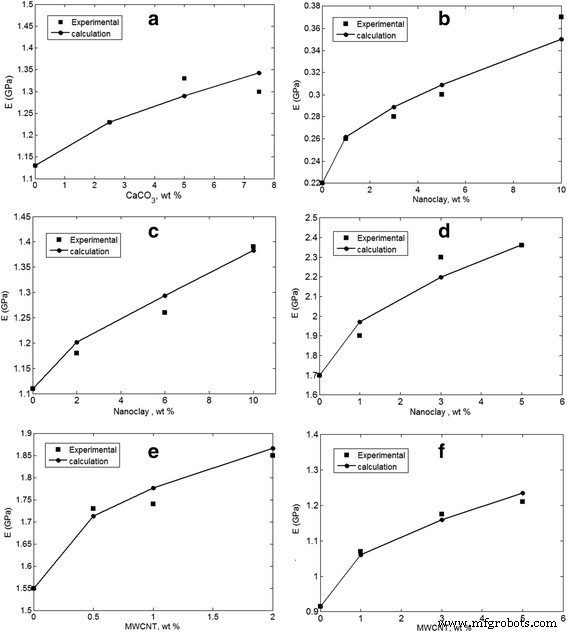
Разница между экспериментальными и теоретическими результатами, предполагающими агломерацию / агломерацию наночастиц для a ПВХ / CaCO ₃ [30], b PCL / наноглина [31], c АБС / наноглина [32], d PLA / наноглина [33], e ПЭТ / МУНТ [34] и f полиимид / MWCNT [35] образцы

Наибольший и наименьший модули, предсказанные текущей методологией, вычисляются и проиллюстрированы на рис. 3 при среднем значении E . _м =2 ГПа и E _f =200 ГПа. Максимальный модуль достигается при наименьших значениях « z . »И« y ”Параметры; например, z =0,00001 и y =0,00001 (не может быть 0). С другой стороны, « y ”Уровень 0,99 приводит к агломерации / агломерации всех наночастиц, что значительно снижает модуль. Кроме того, наивысший уровень « z ”(Максимальная степень агломерации) обуславливает минимальный модуль упругости. « z ”, Поскольку объемная доля агломерированного наполнителя в нанокомпозите меньше объемной доли всех наночастиц ( ϕ _f ). Итак, z = ϕ _f может предложить малейший уровень модуля. Существенная разница между верхним и нижним значениями модуля показывает важную роль агломерации / агломерации наночастиц в жесткости нанокомпозитов. Агрегация / агломерация наночастиц в нанокомпозитах значительно снижает модуль Юнга при различных концентрациях наполнителя, в то время как тонкая дисперсия наночастиц без агломерации / агломерации дает хороший модуль. Кроме того, высокая агломерация / агломерация при большом содержании нанонаполнителя снижает скорость роста модуля при увеличении « ϕ _f ». Следовательно, важно отрегулировать материал и параметры обработки, чтобы предотвратить агломерацию / агломерацию наночастиц, которые способствуют концентрации напряжений и дефектов или расслоению полимерных нанокомпозитов [37, 38].

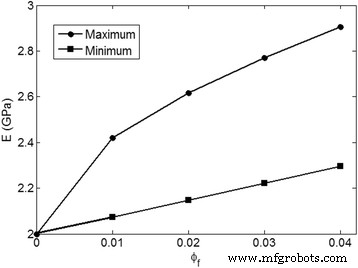
Максимальный и минимальный уровни модуля, прогнозируемые настоящей методологией при среднем значении E _м =2 ГПа и E _f =200 ГПа

На рисунке 4 показано влияние « z »И« y ”Параметры модуля упругости E _м =3 ГПа, E _f =150 ГПа и ϕ _f =0,02. Наивысший модуль достигается на самых маленьких уровнях « z . »И« y ”Параметры, подтверждающие положительную роль хорошей дисперсии / распределения наночастиц на модуле нанокомпозитов. Однако модуль сильно уменьшается как « y »Параметр увеличивается. Согласно формуле. 2, « y ”Показывает концентрацию наночастиц в фазе агломерации / агрегации. Низкий модуль упругости наблюдается при высоком значении « y . ”Уровень, который показывает, что большая часть наночастиц в фазе агломерации / агрегации ослабляет нанокомпозит. Соответственно, агломерированные / агрегированные наночастицы оказывают отрицательное влияние на модуль упругости нанокомпозитов. Следовательно, необходимо приложить большие усилия для облегчения диспергирования / распределения наночастиц в полимерной матрице, которое зависит от межфазного взаимодействия / адгезии между полимером и наночастицами и параметров обработки. Предыдущие исследования сообщили о ценных результатах в этой области и предложили различные методы для улучшения этой дисперсии [39,40,41].

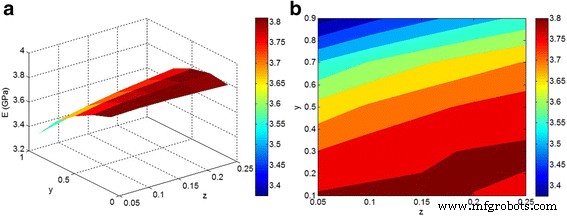
а , b Расчеты модуля по формулам. 10–11 как функция от « z »И« y ”В E _м =3 ГПа, E _f =150 ГПа и ϕ _f =0,02

На рисунке 5 показана зависимость прогнозируемого модуля от « E . _м »И« E _f ”Параметры при среднем ϕ _f =0,02, z =0,3 и y =0,5 при текущей методике. Замечено, что модуль зависит как от « E _м »И« E _f ”Факторы при низком E _f <150 ГПа. Однако более высокий модуль наночастиц не изменяет модуль упругости нанокомпозита. В результате модуль нанокомпозитов зависит только от « E _м », Когда« E _f ”Выше 150 ГПа. Это говорит о том, что высокая жесткость наночастиц не играет главной роли в модуле упругости нанокомпозита, и большое внимание следует уделять диспергированию / агломерации / агломерации наночастиц.

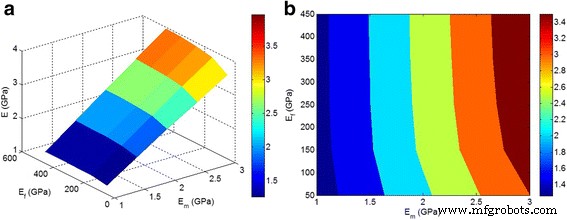
а , b Эффекты « E _м »И« E _f ”От прогнозируемого модуля по формулам. 10–11 в среднем ϕ _f =0,02, z =0,3 и y =0,5

Выводы

Был предложен двухэтапный метод определения влияния агрегированных / агломерированных наночастиц на модуль Юнга полимерных нанокомпозитов. Модели Пола и Максвелла были применены для расчета модулей агломерации / агломерации и эффективных фаз матрицы. Прогнозы предлагаемой методики показали хорошее согласие с экспериментальными данными для различных образцов, при условии правильных параметров агломерации / агломерации. Соответственно, настоящая методология может дать приемлемые результаты для агломерации / агломерации наночастиц в полимерных нанокомпозитах. Агрегация / агломерация наночастиц значительно снижает модуль Юнга, тогда как тонкая дисперсия наночастиц дает высокий модуль. Наивысший модуль был получен при наименьшем значении « z . »И« y ”Параметры, которые подтвердили положительную роль хорошей дисперсии / распределения наночастиц в модуле нанокомпозитов. Однако модуль уменьшается по мере того, как « y »Параметр увеличился. Более того, было обнаружено, что превосходные характеристики наночастиц, такие как высокий модуль, недостаточны для достижения оптимальных свойств в полимерных нанокомпозитах. Соответственно, большое внимание следует сосредоточить на дисперсии / распределении наночастиц в полимерной матрице в зависимости от межфазного взаимодействия / адгезии между полимером и наночастицами и параметров обработки.