Эволюция области контакта при нормальной нагрузке для шероховатых поверхностей:от атомных к макроскопическим масштабам

Фон

Большинство макроскопических поверхностей считаются шероховатыми и фрактальными [1, 2]. Поведение контакта между шероховатыми поверхностями намного сложнее, чем у идеально гладких поверхностей [3, 4]. Реальная площадь контакта образована большим ансамблем дискретных контактных областей (кластеров), который намного меньше видимой площади поверхности. Нормальная сила, размер, форма и распределение кластеров контактов являются ключевыми для выявления поведения контакта, что важно для следующих исследований трения [5,6,7].

Чтобы получить взаимосвязь между площадью контакта и нагрузкой, с 1960-х годов было предложено множество моделей [1, 8, 9, 10, 11, 12, 13, 14]. Среди них модель неровности - самая простая и популярная. В одном из первых приложений модели неровностей Гринвуд и Уильямсон [8] описывают шероховатость поверхности контакта, предполагая, что неровности имеют одинаковый радиус, но разную высоту. С тех пор преобладала модель шероховатости, и в этой области появилось огромное количество литературы. Уайтхаус и Арчард [15] разработали модель Гринвуда и Вильямсона (G-W), учитывая случайные радиусы кривизны вершин неровностей. Наяк [16,17,18] ввел методы теории случайных процессов [19, 20] в анализ гауссовой шероховатости, который впоследствии был использован Бушем и др. [9] при контакте с шероховатой поверхностью.

Одно из основных предположений в модели выступов состоит в том, что взаимодействием между выступами можно пренебречь, что указывает на то, что потенциальные контактные выступы могут быть заранее определены геометрией поверхности. Однако это предположение может привести к неточным оценкам контактного усилия и площади контакта. Чтобы получить эволюцию контактирующих кластеров и взаимодействие между ними, мы используем молекулярную динамику функции Грина (GFMD) [21,22,23] для изучения фрактальной шероховатой поверхности.

Эта работа предназначена для преодоления разрыва между атомным масштабом и макроскопическим масштабом для нормального поведения контакта. Эволюция площади контакта от атомных до макроскопических масштабов продемонстрирована на численных примерах с учетом взаимодействий неровностей. В последующем обсуждении мы сначала кратко представляем наши подходы к генерации фрактальной поверхности, модель GFMD, алгоритм обнаружения контактирующих кластеров и численный экспериментальный план. Затем мы сосредотачиваемся на формировании и развитии контактного кластера и влиянии этих процессов на поведение интерфейса.

Методы

Создание шероховатой фрактальной поверхности

Чтобы изучить контактное поведение шероховатой поверхности, нам необходимо сгенерировать поверхность для численной модели. Для фрактальных поверхностей использовалось несколько алгоритмов [24]. В этой работе мы используем метод преобразования Фурье для создания фрактальных шероховатых поверхностей, как показано на рис. 1. Четыре параметра необходимы для определения фрактальной шероховатой геометрии поверхности. Это максимальная частота ( w _H ), минимальная частота ( w _L ), показатель Херста ( H ) и стандартное отклонение амплитуды ( P ). Основные статистические параметры поверхности, такие как среднеквадратичная высота \ (\ left (\ sqrt {M_0} \ right) \), среднеквадратичный уклон \ (\ left (\ sqrt {M_2} \ right) \) _, и среднеквадратичная кривизна \ (\ left (\ sqrt {M_4} \ right) \) - ключевые параметры поведения интерфейса, где M _я это я -й радиальный момент поверхностного спектра [19, 20]. Стоит отметить, что статистический параметр поверхности M _я относится к статистическим параметрам профиля m _я по следующему уравнению:\ ({M} _0 ={m} _0, {M} _2 =2 {m} _2, {M} _4 =\ frac {4} {3} {m} _4 \). Хорошо известно, что плотность неровностей n (вершины или впадины на поверхности) можно определить по следующему уравнению:

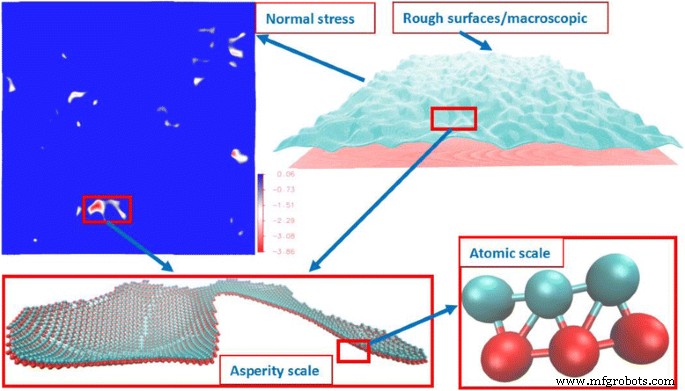
Модель GFMD в разных масштабах, от атомного до макроскопического (в σ )

Кроме того, общее количество вершин / долин на поверхности N выражается

где A ₀ - кажущаяся площадь поверхности. Для самоаффинной фрактальной поверхности статистические параметры поверхности связаны с входными параметрами ( w , H , P ) следующим уравнением:

где B - постоянная шероховатости поверхности, которая связана с P . Уравнения (3) и (2) показывают, что число вершин / впадин фрактальной поверхности зависит от длины волны и показателя Херста. Подробное обсуждение статистических свойств фрактальной поверхности можно найти в литературе [25, 26].

В алгоритме преобразования Фурье в качестве типичного примера мы устанавливаем компонент Херста равным H =0,5, максимальная частота должна быть w _L =1 / (24 σ ), минимальная частота должна быть w _H =1 / (256 σ ), стандартное отклонение амплитуды частоты должно быть P =0,69, а размер системы - 512 × 512 атомов (при начальном расстоянии 1,12 σ ). Эти входные параметры впоследствии создают поверхность со следующими статистическими параметрами:среднеквадратичный уклон поверхности \ (\ sqrt {M_2} =0,077 \) и среднеквадратичная кривизна \ (\ sqrt {M_4} =0,0077 \) . Общее количество вершин / долин на поверхности 150 на основании уравнения. (2), в то время как при численном подсчете число вершин на поверхности составляет 158, а число впадин - 159. Ошибка находится в пределах 5%, что говорит о том, что размер системы является приемлемым в статистическом смысле. Фактически, когда мы увеличиваем размер системы до 2048 × 2048 атомов (при начальном расстоянии, равном 1,12 σ ), результаты для статистических параметров согласуются с результатами для меньшей системы.

Модель GFMD

Взаимодействие между частицами очень сложно зафиксировать экспериментально [6, 27]. В последнее время молекулярная динамика использовалась для моделирования взаимодействия между частицами с целью исследования молекулярного происхождения механизма контакта / трения. Однако затраты на вычисления для крупномасштабного молекулярно-динамического моделирования весьма высоки. Поэтому GFMD вводится для моделирования поверхности из-за его высокой эффективности. GFMD использует молекулярную динамику для моделирования взаимодействия атомов интерфейса (здесь два слоя), в то время как неинтерфейсный слой, который обычно демонстрирует упругое поведение, моделируется функцией Грина. Таким образом, он сводит большую атомную систему к двухслойным атомам на границе раздела (как показано на рис. 1), что резко снижает вычислительные затраты. Подробное обсуждение GFMD можно увидеть в литературе [21,22,23, 28]. В модели GFMD потенциал Леннарда-Джонса (LJ) используется для моделирования межчастичного взаимодействия. Уравнение записывается как

где ε - глубина потенциальной ямы, σ - конечное расстояние, на котором межчастичный потенциал равен нулю, и r - расстояние между частицами. Берем ε , σ , и ε / σ как единицы энергии, расстояния и силы соответственно. По потенциалу LJ мы знаем, что когда r =2 ^1/6 σ ≈ 1,12 σ , межчастичная сила равна нулю. Когда r > 1,12 σ , межчастичная сила притяжения; когда r <1,12 σ , межчастичная сила отталкивающая. Поскольку мы не рассматриваем адгезию в этой работе, расстояние отсечки установлено равным 1,12 σ . Кристаллическая структура, используемая для атомного слоя, является гранецентрированной кубической (ГЦК). Из-за симметрии мы берем только слой интерфейса для формирования геометрии поверхности, как показано на рис. 1, а упругий блок под плоской поверхностью моделируется функцией Грина.

Связь с методом распознавания кластера

На границе раздела наблюдаются три масштаба, как показано на рис. 1:(1) атомный масштаб, который моделируется потенциалом LJ; 2) шкала шероховатости - групповой эффект контактных атомов; и (3) макроскопический масштаб, который представляет собой групповой эффект контактных кластеров. Размер, форма, расположение и распределение контактных кластеров являются важнейшим мостом между молекулярным поведением и свойствами интерфейса. На наномасштабе область атомного контакта определить трудно [6]. Здесь мы определяем контактный атом его нормальной составляющей силой fz> 0. Далее, связанные контактирующие атомы определяются как контактирующий кластер. Для поиска контактирующего кластера используется техника маркировки [29, 30]. Здесь мы используем модифицированный алгоритм ускорения, который позволяет избежать рекурсивного процесса поиска. Блок-схема алгоритма показана на рис. 2, где данные по атомной силе извлечены из молекулярно-динамического моделирования функции Грина. Алгоритм разделен на восемь основных шагов, как показано ниже.

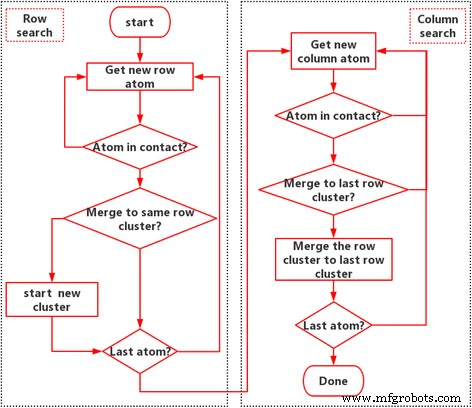
Алгоритм обнаружения контактных кластеров:техника маркировки

Шаг 1. Начните поиск в строке и получите новые данные об атомах, то есть ищите атомы от строки к строке.

Шаг 2. Определите, контактирует ли атом. Если он не находится в контакте, вернитесь к шагу 1. Если он находится в контакте, перейдите к следующему шагу.

Шаг 3. Сравните текущий атом с предыдущим атомом в той же строке. Если предыдущий атом также находится в контакте, объедините атом в кластер, которому принадлежит предыдущий атом, затем пометьте атом тем же номером, что и предыдущий атом. Если предыдущий атом не находится в контакте, пометьте атом новым числом, равным предыдущему числу плюс один.

Шаг 4. Определите, является ли это последним атомом; в противном случае вернитесь к шагу 1 или перейдите к процессу поиска по столбцу.

Шаг 5. Запустите поиск в столбце и получите новые данные об атомах, то есть ищите атомы от столбца к столбцу.

Шаг 6. Определите, контактирует ли атом. Если он не находится в контакте, вернитесь к шагу 5. Если он находится в контакте, перейдите к следующему шагу.

Шаг 7. Сравните текущий атом с предыдущим атомом в том же столбце. Если предыдущий атом также находится в контакте и принадлежит другому кластеру, объедините текущий кластер с кластером, которому принадлежит предыдущий атом, затем пометьте атомы тем же номером и сохраните их. Если предыдущий атом не находится в контакте или принадлежит к тому же кластеру, переходите к следующему шагу.

Шаг 8. Определите, является ли текущий атом последним атомом; в противном случае вернитесь к шагу 5, иначе поиск будет завершен.

Численный экспериментальный дизайн

Хорошо известно, что задачу контакта двух шероховатых поверхностей можно упростить как задачу с одной составной жесткой шероховатой поверхностью и плоской упругой поверхностью, введя эквивалентный модуль упругости E * , который записывается как

где E ₁ и E ₂ - модуль упругости верхней и нижней поверхностей соответственно. Для простоты мы рассматриваем жесткую шероховатую поверхность, контактирующую с упругой гладкой поверхностью, а затем исследуем формирование и развитие контактирующего кластера и его поведение в зависимости от площади. В следующем обсуждении мы будем использовать поверхность, созданную выше (верхняя поверхность жесткая и шероховатая ( E ₁ =∞), а нижняя поверхность гладкая и упругая ( E ₂ =3 ε / σ ³ )) для изучения поведения контакта, где оба элемента v ₁ и v ₂ установлены равными 0,5. Размер нашей системы составляет 512 × 512 атомов (с начальным шагом, равным 1,12 σ ), а периодические граничные условия используются в x - г самолет. Глубина упругого блока составляет 1024 атомных слоя (с начальным шагом, равным 1,12 σ ). При обычном моделировании молекулярной динамики система будет состоять из 268 697 600 атомов; модель GFMD уменьшает число до 524 288 (два слоя атомов), как показано на рис. 1. Мы постепенно вдавливаем шероховатую поверхность (сверху) в плоскую упругую поверхность. Нагрузка жесткой поверхности контролируется перемещением. Каждый шаг нагружения смещения установлен на 0,01 σ , и алгоритм GFMD будет обновлять положение каждого атома до тех пор, пока атомная сила не будет соответствовать критерию конвергенции L ¹ -норма =0,01 ε / σ. Максимальное количество итераций установлено равным 50 000, чтобы избежать бесконечного цикла.

Результаты и обсуждение

Связь с отделом распространения и разработки кластеров

Модель выступов рассматривает выступы как сферические или эллиптические и не учитывает взаимодействие между контактирующими выступами. В этой работе неровности, используемые в модели неровностей, извлекаются из поверхности, созданной выше. В модели неровностей потенциальные неровности, контактирующие с ними, могут быть заранее определены геометрией поверхности на основе их высоты; то есть вершины / долины на поверхности будут формироваться как контактные группы в соответствии с их высотой. Однако в действительности выступ имеет неправильную форму, и обычно несколько смежных выступов могут сливаться в одну большую, как показано на рис. 2. Было замечено, что вначале имеется шесть независимых выступов, и поскольку сила контакта увеличивается, они окончательно сливаются в большой контактирующий кластер (рис. 3). Это говорит о том, что предположение о том, что расстояние между неровностями достаточно велико, чтобы неровности не влияли друг на друга, может привести к неточным результатам.

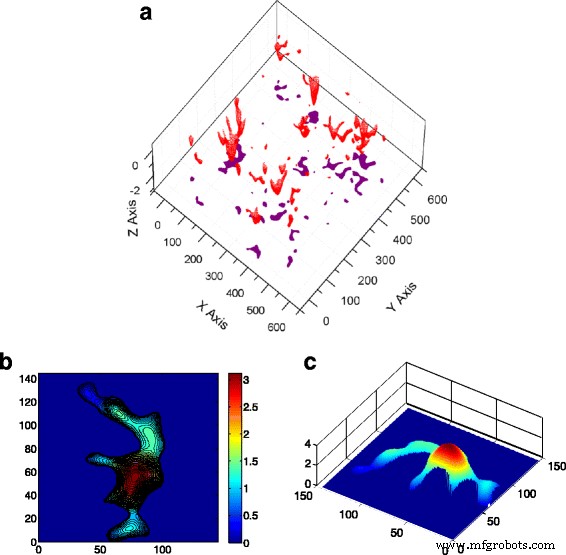
Форма кластеров и эффект слияния. а Трехмерный вид контактных кластеров и его проекция на x - г самолет (в σ ). б Типичный контактный кластер, состоящий из шести независимых неровностей. c Трехмерный вид геометрии контактного кластера (в σ )

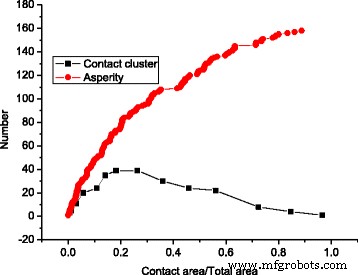
Рисунок 4 демонстрирует, что количество кластеров сначала увеличивается, а затем уменьшается с увеличением площади контакта, в то время как шероховатость поверхности всегда увеличивается с увеличением площади контакта. Это связано с эффектом слияния, показанным на рис. 3.

Поверхностные впадины и количество кластеров под разными контактными площадками

Эффект слияния контактных кластеров наблюдался как в модели неровностей, так и в модели GFMD. Однако при той же площади контакта количество контактных кластеров в модели GFMD намного больше, чем в модели неровностей, как показано на рис. 5. Наблюдается, что количество контактных кластеров в модели GFMD почти вдвое больше, чем в модели выступов, как показано на рис. 5. Основная причина этого состоит в том, что модель выступов не учитывает взаимодействие между шероховатостями. Однако в модели GFMD контактные кластеры влияют друг на друга. Поля смещения, создаваемые контактными кластерами, непрерывны по всей площади поверхности. Смещение большого ансамбля кластеров приводит к новой геометрии на упругой поверхности, что влияет на образование новых контактных кластеров. Следовательно, формирование контактного кластера не только зависит от высоты жесткой шероховатой поверхности, но также может зависеть от деформаций гладкой упругой поверхности. Это также можно наблюдать на рис. 6, где показано распределение контактных кластеров в различных областях для модели выступов и модели GFMD, соответственно. Как показано на рис. 6, при площади контакта 5% номера контактных кластеров равны 17 и 34 для модели шероховатости и модели GFMD, соответственно, в то время как при площади контакта 10% их номера контактных кластеров становятся равными 24 и 52. , соответственно. Это говорит о том, что контактные кластеры в модели GFMD более дискретны, чем в модели неровностей. В модели GFMD средний размер кластера меньше, но большинство кластеров будут совпадать с вершинами / впадинами, как можно наблюдать на рис. 7. Кроме того, модель выступов рассматривает либо долины, либо вершины как потенциальные выступы ( в зависимости от того, какая сторона контактирует). Однако на рис. 8 мы обнаружили, что по мере увеличения площади контакта как вершины, так и впадины могут соприкасаться. На рис. 8 большая часть соприкасающихся неровностей - это углубления на поверхности, когда площадь контакта мала. Однако, когда площадь контакта превышает 10% площади поверхности, все больше и больше вершин также могут образовываться в виде кластеров контакта.

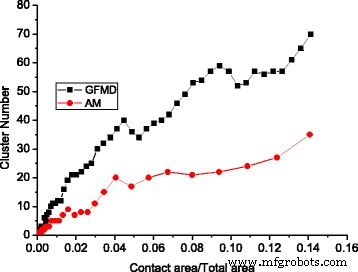
Разработка кластера по разным моделям

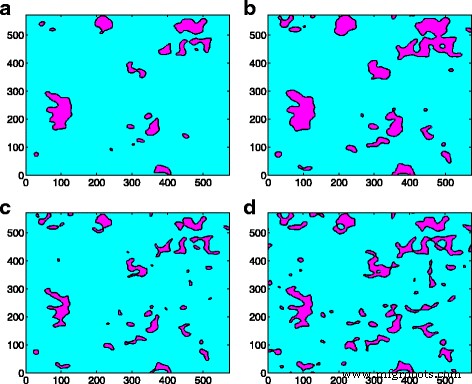
Контур кластерного распределения (в σ ) на разных площадках контакта для модели шероховатости и модели GFMD соответственно. а Модель шероховатости с площадью контакта 5%. б Модель шероховатости с площадью контакта 10%. c Модель GFMD с площадью контакта 5%. г Модель GFMD с площадью контакта 10%

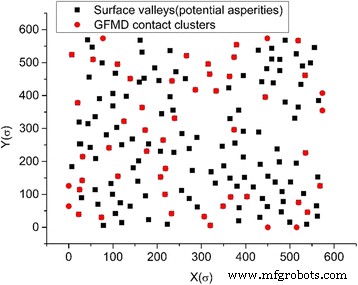
Расположение кластеров контактов и впадин на 10% площади контакта

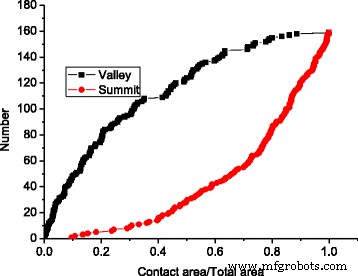
Количество долин на поверхности и вершин растет в разных областях

Взаимосвязь контактной площади и нагрузки

Взаимосвязь силы и площади при нормальной нагрузке важна для поведения контакта. В более ранних моделях неровности обычно считались сферическими и эллиптическими. Однако реальные контактные кластеры намного сложнее. В этом разделе мы сравнили соотношение контактной силы и площади трех моделей:(1) модель GFMD; (2) модель неровностей (обозначена как AM), в которой неровности непосредственно извлекаются с поверхности, прежде чем мы используем GFMD, чтобы протолкнуть эти неровности на плоскую упругую поверхность (это гарантирует отсутствие неожиданного образования кластеров контакта во время контакта); и (3) модель Гринвуда и Уильямсона (обозначена как G-W), в которой шероховатость преобразована в эквивалентную сферу. Радиус сферы определяется

Для модели GFMD и модели выступов с неровностями, извлеченными точно с поверхности, общие силы на границе раздела могут быть получены путем суммирования сил каждого контактного кластера, извлеченных из GFMD. Для модели Гринвуда и Уильямсона мы используем теорию Герца для каждой силы выступов (с тем же свойством материала, что и в модели GFMD), что означает, что общая сила F можно выразить как

где Z _я высота выступов, d - смещение, приложенное к жесткой поверхности, а f - контактная сила неровностей, основанная на теории контакта Герца.

На рис. 9 мы сравнили зависимости силы от площади трех моделей, которые демонстрируют линейные зависимости. Замечено, что общая сила в GFMD намного меньше, чем у модели выступов и модели G-W. F в модели неровностей в 1,80 раза больше, чем предсказано GFMD, и F в модели G-W в 1,54 раза больше, чем прогнозирует GFMD. Это можно объяснить среднеквадратичным наклоном контактных кластеров. Известно, что нормальная нагрузка пропорциональна среднеквадратичному уклону, то есть \ (L \ propto \ sqrt {M_2} \). В модели GFMD область контакта состоит из большего числа кластеров, проникновения которых меньше, чем в модели неровностей. Поскольку наклон вершины выступа меньше, RMS-наклон для контактного кластера в модели GFMD также меньше. На рисунке 10 показаны среднеквадратичные наклоны контактного кластера для трех моделей. Можно видеть, что среднеквадратичный наклон контактных кластеров в GFMD меньше, чем RMS-наклон поверхности, равный 0,077, в то время как среднеквадратичные наклоны контактных кластеров обеих других двух моделей больше, чем RMS-наклон поверхности.

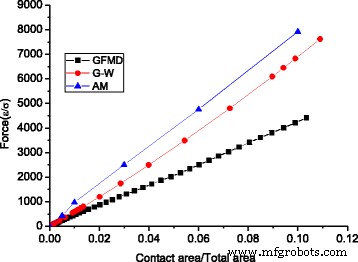
Соотношение площади контакта и нагрузки для разных моделей

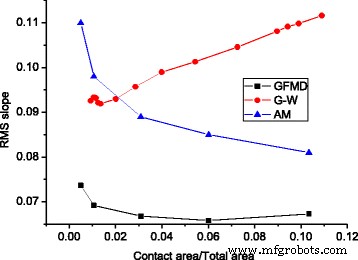
Среднеквадратичный наклон контактных групп с разными площадями контакта для разных моделей, где среднеквадратичный наклон поверхности составляет 0,077

Выводы

Чтобы найти эволюцию площади контакта от атомного до макроскопического масштаба, проблема контакта с шероховатой фрактальной поверхностью была изучена с использованием модели GFMD. Мы определили атомный контакт наличием силы больше нуля и изучили три различных масштаба длины в одной и той же системе. Обнаружено, что межнорельефное взаимодействие существенно для формирования контактного кластера. Некоторые кластеры расположены достаточно близко, чтобы слиться в один большой. Реальная область контакта намного сложнее, чем предсказывается геометрией поверхности из-за упругой деформации в упругой гладкой поверхности. Большинство местоположений контактных скоплений совпадают с вершинами / долинами поверхности. Однако размер кластера меньше, и его формирование не определяется высотой неровностей поверхности. По мере увеличения площади контакта как вершины, так и впадины могут формироваться как контактные кластеры. В модели GFMD сила намного меньше, чем в модели выступов, в то время как количество контактных кластеров в модели GFMD намного больше. Среднеквадратичный наклон контактных кластеров в модели GFMD меньше, чем у модели выступов, что объясняет, почему модель выступов приводит к более высокому давлению. Наши результаты показывают, что реальную площадь контакта нельзя предсказать просто по геометрии поверхности. Фактическая площадь контакта с нормальной нагрузкой важна для следующих исследований трения.