Монослои SnxPy:новый тип двумерных материалов с высокой стабильностью, подвижностью носителей и магнитными свойствами

Введение

Двумерные (2D) бинарные соединения в последние годы привлекли к себе пристальное внимание благодаря своим уникальным свойствам и могут служить надежным ориентиром для их потенциальных приложений в наноэлектронике и оптоэлектронных устройствах [1]. Например, графен вызвал большой интерес с момента своего открытия из-за свойств и потенциальных применений [2,3,4,5,6], тогда как графен имеет необнаруживаемую малую ширину запрещенной зоны при комнатной температуре, что затрудняет его использование в оптоэлектронных наноустройствах. Итак, эти трудности подтолкнули исследователей к поиску 2D-материалов с идеальной запрещенной зоной. В последующие годы нитрид бора (BN) [7], MoS ₂ или другие дихалькогениды переходных металлов [8,9,10,11,12,13] и трихалькогениды переходных металлов [14, 15], среди прочего. В последние годы графен и другие 2D-материалы IV группы (силикон, станен и германен [16]) достигли значительных успехов в научных исследованиях. Кроме того, двумерные полупроводниковые материалы, принадлежащие к группе V, особенно фосфор [17,18,19] и арсенен [20], появляются в качестве претендентов нового поколения в области оптоэлектронных устройств. Фосфен имеет широкие перспективы применения в полевых транзисторах, оптоэлектронных устройствах, спинтронике, газовых сенсорах, солнечных элементах и ​​т. Д., В то время как станен, двумерная сотовая структура, считается новым типом материала с превосходными физическими свойствами после графена. из-за сильной спин-орбитальной связи электронов.

Чтобы получить новые многофункциональные 2D-материалы, необходимо синтезировать два вида элементов. Сообщается, что легирование часто используется для улучшения свойств 2D-материалов с целью расширения сферы их применения. Например, 2D MoS _2x Se _{2 (1 - x )} и WS _2x Se _{2 (1 - x )} нанолисты [21, 22] демонстрируют странные свойства, такие как настраиваемые электронные, оптические свойства и отрицательный коэффициент Пуассона в плоскости с x / г (1/1, 1/2, 1/3 и т. Д.) Координационное число. В качестве другого примера, 2D-материал сплава Si _x С _y [23], B _x С _y [24], и B _x Si _y [25] показывают много новых характеристик (новомодная структура, электронные и механические свойства) с помощью расчетов из первых принципов, которые отличаются от характеристик чистого основного состояния. Поскольку двухмерные монослои фосфора и станена обладают новыми свойствами, элементы Sn и P были составными с различной стехиометрией.

В этой работе мы построили несколько структур с помощью алгоритма оптимизации роя частиц (PSO). Затем мы выделили четыре наиболее устойчивые структуры 2D Sn _x P _y монослоев с различными координационными числами и исследовали электронные свойства на основе оптимизации теории функционала плотности (DFT). Рассчитанные электронные зонные структуры позволяют предположить, что все стабильные или метастабильные монослои с различными координационными числами являются полупроводниками с непрямой запрещенной зоной. Что еще более важно, Pmc2 ₁ -SnP ₂ Монослой представляет собой прямозонный полупроводник с конечной шириной запрещенной зоны 0,92 эВ в области инфракрасного света. Но помимо этого, Pmc2 ₁ -SnP ₂ структура представляет собой прямозонный полупроводник, который обладает высокой подвижностью электронов ∼ 800 см ² V ^-1 s ⁻¹ , что намного выше, чем у MoS ₂ (∼ 200 см ² V ^-1 s ⁻¹ ). Монослой P \ (\ overline {4} {2} _1 \) m-SnP ₂ структура с уникальной структурой валентной зоны может перейти от немагнитной к ферромагнитной за счет дырочного легирования в соответствии с «критерием Стонера». Рассчитанные электронные зонные структуры предполагают, что все монослои Sn _x P _y представляют собой полупроводники с гибко настраиваемой шириной запрещенной зоны под действием двухосной деформации, позволяющей моделировать деформацию запрещенной зоны четырех структур почти во всем диапазоне видимого света.

Вычислительные методы

Чтобы гарантировать тщательный поиск структурного разнообразия, различные x и y выбор от одного до шести учитывается на основе алгоритма оптимизации роя частиц (PSO) [26]. Результаты поиска однослойных структур относительно стабильны только для y / x ≧ 1.

Для изучения электронной структуры 2D Sn _x P _y Для монослоев с различным координационным числом наши расчеты были выполнены с использованием метода теории функционала плотности плоских волн (DFT) [27, 28], реализованного в Венском Ab-initio Simulation Package (VASP) [29,30,31]. С помощью обобщенного градиентного приближения (GGA) для описания обменно-корреляционной энергии в форме Per-dew-Burke-Ernzerhof (PBE) [32,33,34,35] электрон-ионный потенциал описывается проекционным усилением волновой метод [33]. Энергия отсечки плоской волны была выбрана равной 500 эВ для Sn _x P _y системы соответственно. Достаточно плотная k-точка (9 × 9 × 1) обратного пространства была отобрана в зоне Бриллюэна. Вакуумное пространство, перпендикулярное плоскости между соседними суперячейками, превышает 25 Å, что исключает взаимодействие между репликациями. При вычислении двух последовательных шагов оно установлено как 10 ⁵ эВ как значение сходимости энергии. Во время геометрической оптимизации атомные силы всех структур меньше 0,02 эВ Å ⁻¹ используя метод сопряженных градиентов, пока атомы не достигнут своего оптимального положения. Кроме того, мы будем использовать суперячейку с 4 × 4 × 1 для расчета ab initio молекулярной динамики (AIMD), когда алгоритм Нозе [36] на 300K.

На подвижность носителей в основном влияет рассеяние акустической боковой волны, рассеяние боковой оптической волны и рассеяние на ионизированных примесях. Поскольку последние два не так важны, как первый, рассчитанная нами подвижность включает подвижность при рассеянии акустических боковых волн. Мобильность в основном влияет на две характеристики транзисторов:во-первых, концентрация носителей вместе определяет проводимость (обратную сопротивлению) полупроводникового материала. Во-вторых, это влияет на рабочую частоту устройства. Основным ограничением частотных характеристик биполярных транзисторов является время, когда неосновные носители пересекают базовую область. Подвижность - важный параметр для измерения проводимости 2D полупроводниковых материалов. Он определяет проводимость полупроводниковых материалов и влияет на скорость работы устройств. Таким образом, подвижность носителей определяется дисперсией фононов и может быть описана теорией деформационного потенциала (ДП), предложенной Бардином и Шокли [37]. Итак, подвижность носителей в 2D-материалах может быть выражена как [38, 39]

где e , ℏ и k _B - приведенный заряд электрона, постоянная Планка и Больцмана соответственно. И Т - это температура, установленная на 300 К. Где m * эффективная масса, E ₁ - постоянная потенциала деформации, а C ^2D жесткость в плоскости.

Линейное влияние системы на световое поле под малым волновым вектором определяется мнимой частью комплексной диэлектрической проницаемости и диэлектрической проницаемостью, которые могут быть вычислены с помощью

где ε ₁ ( ω ) и ε ₂ ( ω ) являются действительной частью функции и мнимой частью, ε ₁ ( ω ) может быть получено из мнимой части ε ₂ ( ω ) диэлектрическая проницаемость по Крамеру – Кронигу может быть выражена [40]. Мнимую часть диэлектрической функции можно выразить как

Кроме того, коэффициент поглощения I ( ω ) был получен

где C - зона проводимости, V - состояния валентной зоны, Ω - объем элементарной ячейки, м - масса свободных электронов, e - заряд свободных электронов, а ω - частота падающих фотонов.

Результаты и обсуждение

Стабильность

Сначала четыре 2D Sn _x P _y монослои считались определяющими для их энергетической устойчивости. Энергия образования - это энергетический параметр термодинамической системы, который является ключевым моментом для проверки устойчивости системы. Относительная стабильность Sn _x P _y монослои могут быть подтверждены путем вычисления энергии формации и рассчитываются как

где E - энергия соединения или составляющего элемента при определенном давлении. N - количество атомов в элементарной ячейке. Отрицательная энергия образования рассчитанной системы свидетельствует о том, что конфигурация является стабильной или метастабильной [41]. Расчетные энергии образования Sn _x P _y монослои составляют -0,235, -0,223, -0,159 и -0,016 эВ / атом (показаны в таблице 1) соответственно. По его определению меньшее значение указывает на более высокую стабильность. Очевидно, что P \ (\ overline {6} \) m2-SnP является наиболее устойчивой из этих четырех структур. В частности, высокая термическая стабильность полупроводниковых материалов особенно важна при применении электронных устройств. Здесь термостабильность Sn _x P _y монослои исследовали с помощью моделирования неэмпирической молекулярной динамики (AIMD). Основываясь на симметрии пространственных групп, мы просто вычисляем устойчивость P \ (\ overline {6} \) m2-SnP для аналогичных структур P \ (\ overline {6} \) m2-SnP и Pmc2 ₁ -SnP ₂ и Pmc2 ₁ -SnP ₂ для Pmc2 ₁ -SnP ₂ и P \ (\ overline {4} {2} _1 \) m-SnP ₂ конструкции. Результаты показывают, что среднее значение полной энергии структуры остается почти неизменным, а структура остается неизменной через 1 пс, 3 пс и 5 пс, предполагают, что Sn _x P _y монослои термически стабильны (на рисунке S1). Затем мы вычислили кривые дисперсии фононов и отсутствие воображаемых частот колебаний означает, что структуры динамически устойчивы (на рисунке S1). В литературе сообщалось о нескольких методах синтеза слоистых материалов, включая микромеханическое расщепление [2], эпитаксиальный рост [42], химическое осаждение из паровой фазы [43] и жидкостное расслоение [44]. Некоторые материалы с подобной структурой были успешно получены экспериментально. Мы нашли некоторые связанные отчеты о том, что несколько слоев нанолистов GaSe были превращены в высокоэффективный фотодетектор в эксперименте [45]. Кроме того, приготовление, изоляция и быстрая однозначная характеристика сверхтонких слоев большого размера MoS ₂ , GaS и GaSe, нанесенные на SiO ₂ Сообщается о подложках / Si [46].

Как показано на рис. 1a, b, структуры P \ (\ overline {3} \) m1-SnP демонстрируют структуру, аналогичную гексагональной фазе P \ (\ overline {6} \) m2-SnP. Pmc2 ₁ -Sn P ₂ тригональная фаза (рис. 1c) показывает, что x / г состав дополнительно увеличивают до 1/2. Материал конструкции похож на P \ (\ overline {4} \) 2 ₁ м-SnP ₂ была доказана устойчивость теоретическим расчетом [47]. Кроме того, новое исследование обнаруживает структуру XY ₂ (Рис. 1d) является полупроводником с непрямой запрещенной зоной и может быть восприимчив к электрическому полю и напряжению. Мы уверены, что прогнозируемый нами материал будет успешно готовиться в будущем с развитием технологий.

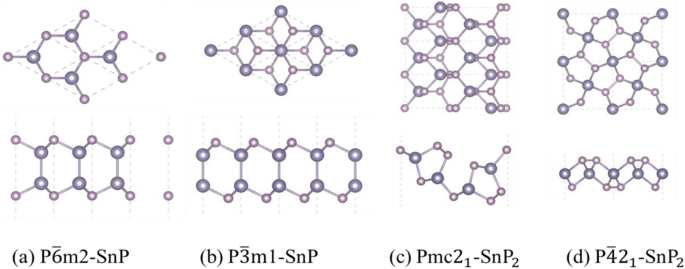
Вид сверху и сбоку на атомные структуры Sn _x P _y монослои: а P \ (\ overline {6} \) m2-SnP, b P \ (\ overline {3} \) m1-SnP, c Pmc2 ₁ -SnP ₂ , и d P \ (\ overline {4} {2} _1 \) m-SnP ₂ ; уровень Ферми (горизонтальная пунктирная линия) смещен до 0 эВ. Тяжелые розовые сферы представляют атомы Sn, а светло-розовые сферы представляют атомы P

Электронные и магнитные свойства

Вычисленные зонные структуры и парциальная плотность состояний Sn _x P _y монослои представлены на рис. 2. Как показано на рис. 2а, P6̅m2-SnP является непрямым полупроводником с шириной запрещенной зоны 1,19 эВ. Максимум валентной зоны (VBM) в направлении Γ → K обеспечивается гибридизированными Sn-p- и P-p-орбиталями, в то время как минимум зоны проводимости (CBM) в точке K происходит из гибридизированных Sn-s- и P-p-орбиталей. P \ (\ overline {3} \) m1-SnP имеет такую ​​же электронную зонную структуру, что и аналог P \ (\ overline {6} \) m2-SnP, но с меньшей шириной запрещенной зоны 1,21 эВ. Дисперсия валентной зоны P \ (\ overline {6} \) m2-SnP и P \ (\ overline {3} \) m1-SnP вблизи точки Γ и уровня Ферми ( E _F ) является довольно плоским, учитывая довольно высокую плотность состояний (DOS) и сингулярность Ван Хова вокруг VBM. Pmc2 ₁ -SnP ₂ имеет прямозонный полупроводниковый характер ( E _g (прямой) - E _g (непрямой) =6 мэВ) с шириной запрещенной зоны 0,72 эВ (см. рис. 2в). Его VBM в основном приписывается P-p-орбиталям, в то время как CBM в основном обеспечивается P-p-орбиталями и Sn-s-орбиталью. P \ (\ overline {4} {2} _1 \) m -SnP ₂ полупроводник с непрямой запрещенной зоной с E _г 1,79 эВ, а полосы, полученные из рис. 2в. Что еще более важно, P \ (\ overline {4} {2} _1 \) m-SnP ₂ монослой имеет аналогичное состояние по сравнению с рис. 2a, b, также возникает характер дисперсии плоских полос вокруг VBM, что приводит к очень высокой плотности состояний и сингулярности Ван Хова.

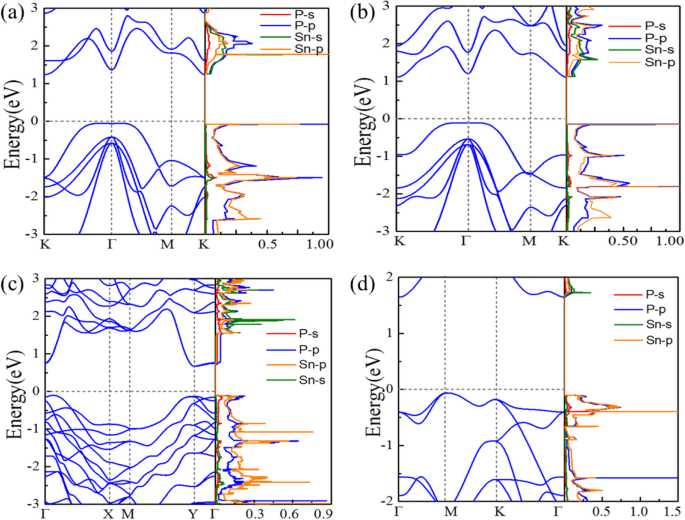
Расчетные электронные зонные структуры и парциальная плотность состояний VBM и CBM Sn _x P _y монослои: а P \ (\ overline {6} \) m2-SnP, b P \ (\ overline {3} \) m1-SnP, c Pmc2 ₁ -SnP ₂ , и d P \ (\ overline {4} {2} _1 \) m-SnP ₂

Согласно критерию Стонера, спонтанный ферромагнетизм возникает, если кинетическая энергия меньше энергии обменного расщепления, то есть, если DOS при E _F достаточно высока. Рисунок 2d показывает очень высокую DOS вокруг VBM; P \ (\ overline {4} {2} _1 \) m-SnP ₂ может удовлетворять критерию Стонера, если его E _F перемещается в положение с высокой плотностью состояний сквозного легирования. Как показано на рис. 3а, дырочное легирование может вводить магнитные моменты при соответствующих концентрациях легирования. Как и ожидалось, результат вычислений предполагает, что P \ (\ overline {4} {2} _1 \) m-SnP ₂ может быть преобразовано в основное ферромагнитное состояние за пределами критической плотности дырок. Среди них плотность отверстий n _h можно выразить как n _h = м _h / S _ячейка , где S _ячейка и м _h - площадь примитивной ячейки и количество отверстий, введенных в примитивной ячейке. Инъекция отверстия в монослой P \ (\ overline {4} {2} _1 \) m-SnP ₂ действительно приводит к ферромагнетизму. Магнитный момент показывает резкую зависимость, напоминающую пик, с плотностью дырок. Поскольку значительный спиновый момент индуцируется дырочным допированием в системе, структура энергетических зон вокруг уровня Ферми сильно изменилась из-за спинового расщепления. В частности, спин-поляризованная зонная структура (показанная на рис. 3b) P \ (\ overline {4} {2} _1 \) m-SnP ₂ при 7,2 × 10 ¹⁴ см ⁻² показывает, что монослой становится идеальным полуметаллом. Итак, мы предсказываем, что стабильное FM-состояние с половинной металличностью может быть реализовано в P \ (\ overline {4} {2} _1 \) m-SnP ₂ монослой.

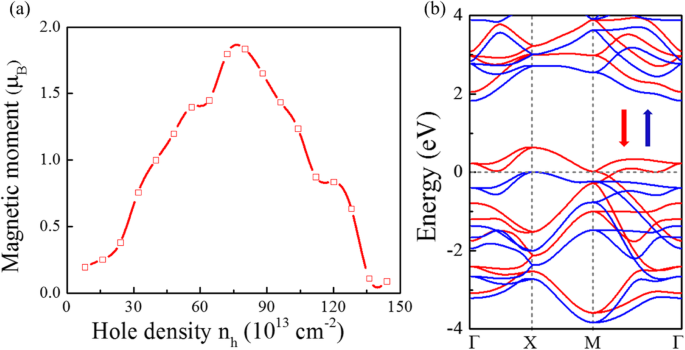
Ферромагнетизм в P \ (\ overline {4} {2} _1 \) m-SnP ₂ монослой. ( а ) Спиновые моменты в зависимости от плотности дырок n _h . б Расчетная структура валентной зоны P \ (\ overline {4} {2} _1 \) m-SnP ₂ в n _h =7,2 × 10 ¹⁴ см ⁻² . Полосы увеличения и уменьшения показаны синим и красным цветом соответственно. Уровень Ферми установлен на 0 эВ

Упругая анизотропия и подвижность носителей монослоя

Влияние деформации на электронные свойства двумерных монослоев Sn _x P _y конструкции тоже интересны. На рис. 4а показано изменение запрещенной зоны при двухосной деформации ε . . Запрещенная зона Sn _x P _y монослои заметно модулируются по некоторым правилам. Например, запрещенная зона P \ (\ overline {6} \) m2-SnP уменьшается с 1,19 до 0,52 эВ с увеличением деформации растяжения до ε =8%, сначала увеличиваясь с 1,12 до 1,36 эВ для ε 2%, затем снижается с 1,36 до 0,51 эВ. Кроме того, поскольку a и b параметра решетки Pmc2 ₁ -SnP ₂ структуры разные, изменения электронных свойств разные по x -axis и y -ось [48], как показано на рис. 4b. Очевидно, что при приложении одноосной деформации в разных направлениях изменение x направление отличается от изменения y направление. Учитывая диапазон энергетических щелей с деформацией ε , диапазон регулируемой ширины запрещенной зоны за счет деформации в плоскости почти покрывает всю область видимого света на основе расчета из первых принципов.

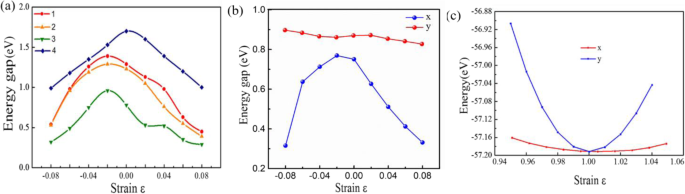
Деформационно-зависимые электронные свойства структур:(1) P \ (\ overline {6} \) m2-SnP, (2) P \ (\ overline {3} \) m1-SnP, (3) Pmc2 ₁ -SnP ₂ и (4) P \ (\ overline {4} {2} _1 \) m-SnP ₂ . б Электронные свойства Pmc2 ₁ , зависящие от одноосной деформации -SnP ₂ . c Энергия Pmc2 ₁ -SnP ₂ монослой против одноосного окрашивания

Кроме того, мы также исследовали влияние одноосного напряжения, как показано на рис. 4c. Жесткость в плоскости C ^2D ( C ^2D =[∂ ² E / ∂ δ ² ] / S ₀ , где S ₀ это площадь 2D Pmc2 ₁ -SnP ₂ монослой) можно получить, подбирая параболу. Интересно, что жесткость в плоскости C ^2D демонстрируя чрезвычайно очевидную упругую анизотропию вдоль a и b направления рассчитаны как 12,1 и 105,6 Н / м соответственно. Поскольку Pmc2 ₁ -SnP ₂ имеет прямозонный полупроводниковый характер, эффективные массы ( m ^∗ = ℏ ² ( ∂ ² E / ∂K ² ) ⁻¹ ) электронов ( м _e составляет | м ^* _e |) и отверстия ( м _h составляет | м ^* _h |), связанный с (квази) прямым полупроводником Pmc2 ₁ -SnP ₂ монослой. Перечислены эффективные массы (таблица 2). Наиболее интересна эффективная масса электронов в k _б направление (0,15 меня) намного меньше, чем в k _а направление (1,31 мэ), что указывает на легкий дрейф электронов в k _б направление. Еще один важный параметр - константа DP E . ₁ ( E ₁ =d E _край / d δ ) для электронов вдоль a и b направления рассчитаны равными 5,36 и 11,57 эВ соответственно. Удивительно, но расчетная несущая может достигать ~ 800 см ² . V ^-1 s ⁻¹ в k _б направление. Для сравнения, мобильность MoS ₂ монослой ∼ 200 см ² V ^-1 s ⁻¹ в экспериментах [8]. Однако подвижность носителей составляет примерно ∼ 8 см ² . V ^-1 s ⁻¹ в k _а направление. Следовательно, высокая подвижность носителей, обнаруженная в этом исследовании, имеет большое значение для изучения электронного транспорта.

Оптические свойства

Фотоэлектрические свойства фотоэлектронных материалов характеризуются диэлектрической функцией, фотопроводимостью и коэффициентом поглощения. Мнимые части диэлектрической проницаемости показаны на рис. 5а. Обратите внимание, что Pmc2 ₁ -SnP ₂ монослой показывает поглощение, начинающееся с ~ 0,70 эВ, и появляются три основных пика поглощения при ~ 0,9, ~ 3,2 и ~ 4,0 эВ. Как показано на рис. 5b, он показывает поглощение во всех трех направлениях в видимом диапазоне и ультрафиолетовом диапазоне для монослоя Pmc2 ₁ -SnP ₂ . Итак, Pmc2 ₁ -SnP ₂ однослойные материалы могут быть использованы для атомарно тонких солнечных слепых фотодетекторов, например, для эффективного обнаружения пламени.

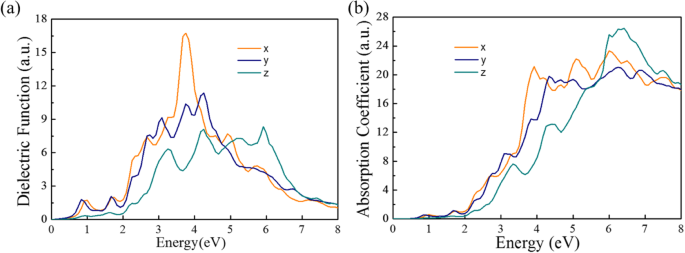
а Вычисленные диэлектрические функции в зависимости от энергии для Pmc2 ₁ -SnP ₂ вдоль разных направлений падающего света. б Расчетный мнимый коэффициент поглощения

Выводы

В заключение, на основе алгоритмов PSO в сочетании с расчетами из первых принципов мы идентифицировали несколько 2D Sn _x P _y монослои с соотношением x / г =1:1 и 1:2. Удивительно, но эти новые монослои также обладают особыми электронными и магнитными свойствами:монослой P \ (\ overline {4} {2} _1 \) m-SnP ₂ структура с уникальной структурой валентной зоны может перейти от немагнитной к ферромагнитной за счет дырочного легирования в соответствии с «критерием Стонера»; Pmc2 ₁ -SnP ₂ структура представляет собой прямозонный полупроводник с плоской упругой анизотропией, обладающий высокой подвижностью электронов до 800 см ² V ^-1 s ⁻¹ вдоль k _б направление, которое намного выше, чем у MoS ₂ (∼ 200 см ² V ^-1 s ⁻¹ ). Пик оптического поглощения материала находится в ультрафиолетовой области. Эти открытия расширяют потенциальные области применения развивающейся области 2D Sn _x P _y структуры в наноэлектронике. Эти желательные свойства многофункционального Sn _x P _y монослои обеспечивают многообещающее применение в электронике и оптоэлектронике.

Доступность данных и материалов

Все они есть в основном тексте и на рисунках.