Спин-поляризованный транспорт и спин-эффект Зеебека в тройных квантовых точках со спин-зависимыми связями между точками

Введение

Наряду с развитием спинтроники [1–3] в последние два десятилетия большое внимание уделяется спиновой калоритронике [4, 5]. В спинтронике одной из наиболее привлекательных задач является управление спином электронов с помощью электрического смещения. В то время как в спиновой калоритронике метод управления вращением - это, в основном, тепловое смещение, температурный градиент, применяемый между разными концами системы. Он рассматривается как сочетание спинтроники и термоэлектричества. Особый интерес представляет спиновый эффект Зеебека (SSE), который генерирует чистый спиновый ток без сопровождающего его зарядового эквивалента, или спиновое смещение, характеризующееся разделением химических потенциалов со спином вверх и вниз. Это открывает способ использования избыточного тепла, выделяемого в наноструктурах, для снижения энергопотребления и повышения производительности тепловых устройств. Такой тип устройства также эффективен при обнаружении градиента температуры системы с помощью степени свободы спина носителей. С 2008 г. К. Учида и др. Постоянно сообщали о некоторых крупных экспериментальных достижениях в наблюдении SSE. в магнитных металлах [6], ферромагнитных изоляторах [7, 8] и ферромагнитных металлах [9]. Впоследствии он был изучен в ферромагнитных полупроводниках [10], немагнитных материалах с магнитным полем [11], парамагнитных материалах [12], антиферромагнитных материалах [13], границе раздела металл-ферромагнетик изолятор [14], а также в топологических изоляторах [15–17]. ].

Махан и его коллеги доказали, что дельтовидная форма функции передачи, которая является обычной для низкоразмерных систем, значительно повысит эффективность термоэлектрических устройств [18]. С тех пор нульмерная квантовая точка (КТ) [19, 20], в которой носители ограничены во всех трех измерениях, была тщательно изучена для увеличения коэффициента SSE (спиновой термоЭДС), который указывает на величину генерируемого спинового смещения при состояние обрыва цепи бесконечно малым тепловым смещением [4–6]. В частности, если в системе более одного пути передачи, электроны будут мешать друг другу и могут возникнуть интересные эффекты Дика [21, 22] или Фано [23, 24], характеризующиеся резким изменением функции передачи и проводимости. . Поэтому большое количество работ было посвящено исследованию SSE в различных кольцевых или многолучевых структурах, содержащих КТ [25–33]. Богатые параметры в нем, такие как настраиваемые уровни точек, кулоновское взаимодействие, магнитный поток, спин-орбитальные взаимодействия, асимметрия связей точка-свинец, позволяют эффективно управлять процессами квантовой интерференции, что приводит к гигантской спиновой термоЭДС, величина которой может достигать как такой же или даже выше, чем у зарядного.

Тройные квантовые точки (ТКТ) различной формы были приготовлены в экспериментах и ​​теоретически изучены, в которых основное внимание уделяется диаграмме стабильности, выпрямлению заряда, фрустрации заряда, квантовому интерференционному эффекту и когерентному управлению спином [34–46]. Среди них точки, соединенные в форму кольца, более интересны из-за наличия квантового интерференционного эффекта [39–46]. По сравнению с электронным транспортом термоэлектрический эффект, особенно SSE, редко исследовался в TQD. В настоящей статье мы исследуем SSE в TQD с учетом спин-зависимых межточочных связей (см. Рис. 1). При приложении статического магнитного поля к туннельным переходам между квантовыми точками спин электрона совершает ларморовскую прецессию, и межточечные связи становятся спин-зависимыми [47, 48]. Недавно было также предложено, что, используя осциллирующие магнитные поля и управляемые во времени напряжения на затворе, можно разделить волновые функции электронов с разными спиновыми компонентами на разные КТ, вызывая скорость передачи с разрешением по спину (силу связи) [49, 50]. В некоторых предыдущих работах уже исследовалось влияние спин-зависимой связи между точками на генерацию спинового тока [51, 52]. Здесь мы показываем, что он может сдвигать положения термостатов со вращением вверх и вниз в противоположных направлениях в пространстве точечного уровня, изменяя антирезонансные состояния Фано, в результате чего получается 100 % спин-поляризованные или чисто спиновые термоЭДС, величина которых может быть такой же большой, как и зарядовая. Такой эффект сильно отличается от случая спин-независимой межточечной связи [53, 54]. Интересно, что полученные результаты могут быть выполнены с очень малой спиновой поляризацией межточечных связей.

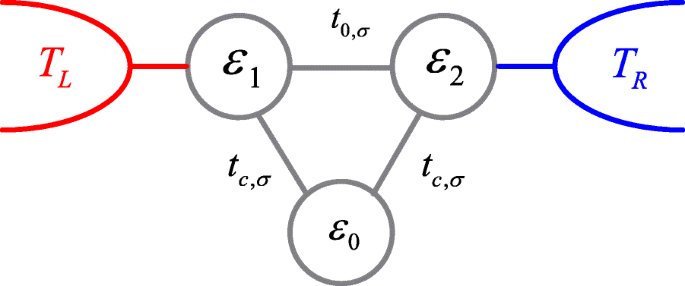
Схема системы тройных квантовых точек. Применяя статическое магнитное поле к туннельным барьерам между точками, межточечные связи становятся спин-зависимыми

Модель и методы

Гамильтониан TQD, показанных на рис. 1, подключенных к двум выводам, может быть смоделирован следующим гамильтонианом Андерсона [25, 33, 51, 52],

где \ (c_ {k \ beta \ sigma} ^ {\ dag} \ left (c_ {k \ beta \ sigma} \ right) \) с β = L , R и \ (d_ {i \ sigma} ^ {\ dag} \ left (d_ {i \ sigma} \ right) \) с i =0,1,2 - соответственно операторы создания (уничтожения) в отведении- β и точка- i со спином σ . Мы предполагаем, что каждая точка включает один уровень энергии ε _я и не учитывает кулоновское взаимодействие между электронами в точках и выводах. QD-1 и QD-2 связаны друг с другом межточечной связью t _{0, σ} = t ₀ (1+ σ p ), а к левому и правому выводам - ​​с помощью точечного соединения V _kL и V _кР , соответственно. QD-0 соединен с QD-1 и QD-2 с силой t _{c , σ} = t _c (1+ σ p ), где σ =± 1 для электронов со спином вверх и вниз соответственно.

В режиме линейного отклика мы можем индивидуально записать спин-зависимые электрический и тепловой токи при бесконечно малой разности потенциалов Δ V и разница температур Δ Т между левым и правым отведениями как [25, 33]

где e - заряд электрона и T температура равновесия системы. Коэффициенты K _{n , σ} в приведенном выше уравнении задаются формулами [25, 33]

где \ (\ hbar \) - приведенная постоянная Планка, μ химический потенциал отведений, f ( ε , μ ) =1 / {1 + exp [( ε - μ ) / k _B Т ]} функция распределения Ферми с постоянной Больцмана k _B .

В формуле. (4) коэффициент передачи T _σ ( ε ) для каждой компоненты спина можно получить в терминах запаздывающей функции Грина как [25, 33] \ (T _ {\ sigma} (\ varepsilon) =\ Gamma _ {L} \ Gamma _ {R} \ left | G_ { 21, \ sigma} ^ {r} (\ varepsilon) \ right | ^ {2} \), где \ (\ Gamma _ {L (R)} =2 \ pi \ sum _ {k} | V_ {kL ( R)} | ^ {2} \ delta \ left [\ varepsilon - \ varepsilon _ {kL (R)} \ right] \) - функция ширины линии. Применяя метод уравнения движения, мы можем легко получить аналитический вид \ (G_ {21, \ sigma} ^ {r} (\ varepsilon) \) как [55, 56]

где \ (\ tilde {\ varepsilon} _ {1 (2)} =\ varepsilon - \ varepsilon _ {1 (2)} + i \ Gamma _ {L (R)} / 2 \). Тогда коэффициент передачи получается как [55, 56]

Термоэдс (коэффициент Зеебека) каждой спиновой составляющей S _σ рассчитывается при условии исчезновения тока заряда Дж _e = Дж _{e , ↑} + J _{e , ↓} =0 и задается формулой [25, 33] S _σ =- К _{1, σ} / ( e Т К _{0, σ} ), а термоЭДС заряда (спина) определяется как S _{c ( s )} = S _↑ + (-) S _↓ .

Результаты и обсуждения

В следующих численных расчетах мы выбираем функцию ширины линии Γ _L = Γ _R = Γ ₀ =1 в качестве единицы энергии и зафиксируем μ =0 в качестве нулевой точки энергии. Константы e , k _B , и h все установлены равными 1. На рисунке 2 показана спин-зависимая проводимость G _σ и термоЭДС S _σ как функции уровня точки ε ₀ = ε ₁ = ε ₂ для t ₀ =0, т.е. TQD соединены последовательно. Когда межточечные связи не зависят от спина ( p =0), проводимости при вращении вверх и вниз на (a) и (b) одинаковы и образуют пик с центром в ε ₀ =0 (черные сплошные линии).

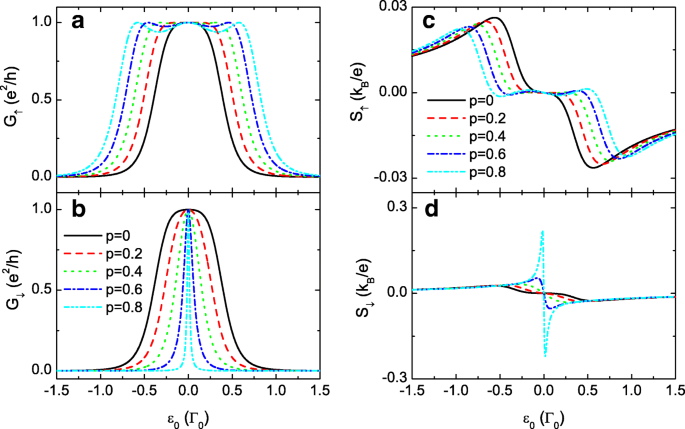
Электропроводность и термоЭДС для t ₀ =0. Спин-поляризованная проводимость G _σ через а и b , и термоЭДС S _σ в c и d как функции уровня точки ε ₀ для фиксированного t ₀ =0 и различные значения спиновой поляризации межточечных взаимодействий. Остальные параметры - отстройка уровня Δ =0, температура T =0,001 и t _c =0,3

При наличии спин-зависимой межточечной связи p 0, единственный пик проводимости при вращении вверх G _↑ на рис. 2а превращается в конфигурацию с тройным пиком с неизменным максимальным значением пика из-за улучшенного межточечного взаимодействия раскрутки вверх t _{c , ↑} . В то время как G _↓ остается паттерн с одним пиком с уменьшенной шириной пика из-за меньшего t _{c , ↓} . Для t _{0, σ} =0 и одинаковые уровни КТ ( ε ₁ = ε ₂ = ε ₀ ), коэффициент передачи в уравнении. (6) сводится к

В функции пропускания есть три резонанса, расположенные соответственно при ε = ε ₀ и \ (\ varepsilon =\ varepsilon _ {0} \ pm \ sqrt {2t_ {c, \ sigma} ^ {2} + \ Gamma _ {0} ^ {2} / 4} \). В условиях низкой температуры в проводимости появляются три резонансных пика при ε ₀ = мк и \ (\ varepsilon _ {0} =\ mu \ pm \ sqrt {2t_ {c, \ sigma} ^ {2} + \ Gamma _ {0} ^ {2} / 4} \) соответственно. В случае слабой связи между точками три пика сливаются в конфигурацию с одним пиком, как показано черными линиями на рис. 2а и. С увеличением междоточечной спиновой поляризации p , значение t _{c , ↑} = t _c (1+ p ) увеличивается, и три пика проводимости со спином вверх разделены в энергетическом пространстве, как показано на рис. 2а. Между тем величина t _{c , ↓} становится меньше и G _↓ на рис. 2б, соответственно, сохраняется картина с одним пиком. Из уравнения. (6) также видно, что ширина пика уменьшается при уменьшении t _{c , ↓} .

Когда p =0, термоЭДС каждой компоненты спина на рис. 2c и d идентичны и антисимметричны относительно точки электронно-дырочной симметрии ( ε ₀ =0), что согласуется с предыдущими работами [33, 57]. Из-за наличия температурного градиента, вызывающего термоэлектрический эффект, температура левого вывода выше, чем у правого, и больше электронов выше химического потенциала μ в левом отведении. Соответственно дыр ниже μ больше . Когда уровни энергии квантовых точек ниже (выше) μ , основными носителями являются дырки (электроны) и тогда термоЭДС положительна (отрицательна) [57]. Термоэдс меняют свой знак при ε ₀ =0 из-за компенсации электронов и дырок. При увеличении p , ширина пика ускоряющейся термоЭДС S _↑ увеличивается с уменьшенным пиковым значением. Тогда как спина сужается. Интересно, что пиковое значение S _↓ очевидно усиливается увеличением p . Для случая большой спиновой поляризации между точками, например p =0,8, пиковое значение S _↓ примерно в десять раз больше S _↑ с почти неизменным значением спин-зависимой проводимости G _σ . Это можно объяснить следующим образом. Для положительного p , скорость межточечного туннелирования t _{c , ↑} > т _{c , ↓} и электроны (или дырки) со спином вверх будут проходить через квантовые точки быстрее, чем электроны со спином вниз. Соответственно, больше электронов (дырок) со спином вниз блокируется в левом (правом) отведениях по сравнению с электронами со спином вверх, что приводит к большему напряжению вращения вниз в ответ на температурный градиент.

Чтобы еще больше увеличить разницу между S _↓ и S _↑ , мы представляем результаты очень большого p на рис. 3. Мы находим, что проводимость при раскручивании вверх G _↑ и термоЭДС S _↓ меньше подвержены влиянию изменения p , который для сравнения показан на вставках к рис. 3а и б. При увеличении p носители со спином вниз становится еще труднее переносить через квантовые точки и будут накапливаться на выводах. Соответственно, значение G _↓ монотонно подавляется, но пиковое значение S _↓ заметно увеличен, предлагая эффективные средства для генерации полностью спин-поляризованной термоЭДС за счет спин-зависимой межточечной связи. Этот результат также может быть многообещающим при обнаружении градиента температуры в системе методом SSE. Теперь, когда слабая связь между точками увеличивает значение термоЭДС, мы выбираем меньшее значение t _c с фиксированным p =0,7 на рис. 4. В этом случае три резонансных пика в проводимости как со спином вверх, так и со спином вниз сливаются в один. Ширина пика проводимости увеличивается при увеличении t _c что согласуется с предыдущими результатами. Рис. 4b и d показывает, что величина обоих S _↑ и S _↓ усиливается за счет уменьшения t _c . Максимумы термоЭДС при замедлении вращения также могут достигать около 4 k _B / e для t _c =0,02 Γ ₀ . В экспериментах межточечные связи регулируются напряжением на затворе или толщиной туннельного барьера. Следовательно, может оказаться более целесообразным увеличить термоэдс, изменив t _c с фиксированной спин-поляризацией p , поскольку магнитное поле обычно труднее контролировать, чем электрическое. Фактически, большая термоЭДС может быть получена с очень маленьким p при некоторых условиях, как показано ниже.

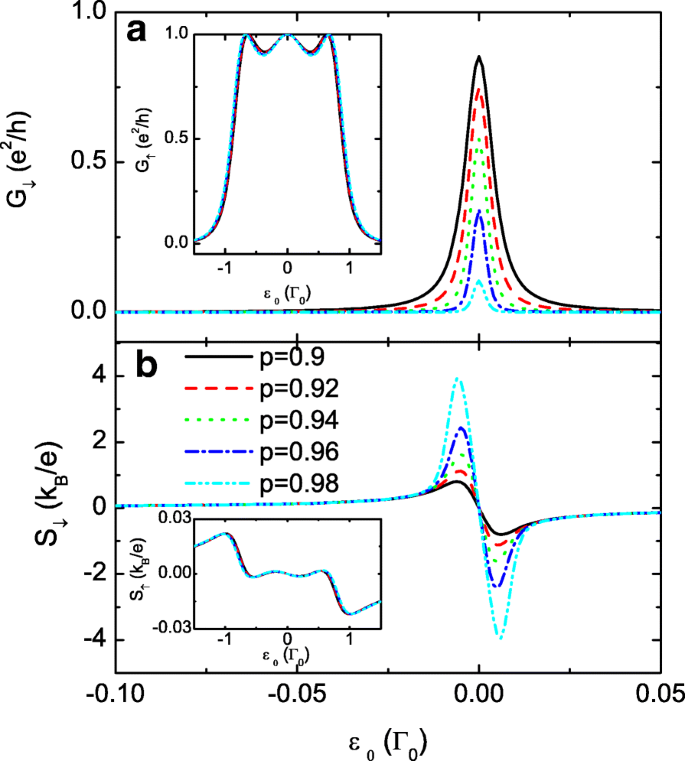
Снижающая проводимость и термоЭДС. Электропроводность при замедлении G _↓ через а и термоЭДС S _↓ в б для случая большой межточечной связи 1> p ≥0.9. Вставка в a для G _↑ в режиме с большими точками, а вставка на b обозначает термоЭДС со спином вверх по сравнению с термоэдс со спином вниз. Остальные параметры как на рис. 2

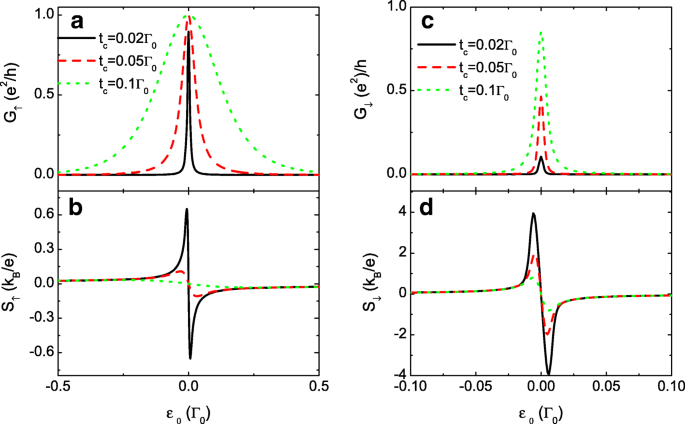
Электропроводность и термоЭДС для разных t _c . Спин-поляризованная проводимость G _σ через а и c , а термоЭДС S _σ в б и d как функции уровня точки ε ₀ для p =0,7 и разные значения t _c . Остальные параметры как на рис. 2

Если квантовые точки соединить в форме кольца, возникший эффект Фано резко изменит свойства проводимости [46] и термоЭДС. В частности, гигантская тепловая энергия возникает вокруг состояния антирезонанса Фано, где функция передачи приближается к нулю T _σ ( ε ) =0 из-за полного отражения [25–33]. Замена энергии электронов на ε химическим потенциалом μ в формуле. (5) можно найти единственное антирезонансное состояние, расположенное в

который определяется исключительно связями между точками и не зависит от других параметров, таких как уровни точек ε ₁ , ε ₂ , температура T или гибридная матрица с точечными выводами Γ _α . Следовательно, регулировать проводимость и термоэлектрические величины в такой сложной системе довольно просто. При условии μ =0, антирезонансное состояние находится только при положительном ε ₀ боковая сторона. На рис. 5а и б показана антирезонансная долина Фано в проводимости. На вставке к рис. 5а показана форма линии Фано проводимости в режиме больших точек. В отличие от случая t ₀ =0, в котором нулевая точка термоЭДС находится в ε ₀ =0, значение t ₀ 0 находится в антирезонансном состоянии, которому термоЭДС антисимметрична. В случае p =0, нулевые точки термоЭДС обеих спиновых компонент находятся при ε ₀ =0,09, как показано на рис. 5c и d. При увеличении p , они разделены и смещены в противоположные стороны на 0,09. По обе стороны от нулевой точки появляется широкий пик с положительными и отрицательными значениями соответственно. Следует отметить, что значение термоЭДС пренебрежимо мало в других режимах с точечными уровнями, что показано на вставке к рис. 5в. Смещение нулевых точек, а также пиков в термоЭДС приводит к двум интересным результатам. Один - 100 % спин-поляризованная термоЭДС, когда пики S _↑ и S _↓ полностью разделены в энергетическом пространстве довольно большими p ценность. См., Например, синюю штрихпунктирную линию на рис. 5c и d для p =0,4. Справа от ε ₀ =0,09, значение S _↓ приближается к нулю, но S _↑ имеет два острых пика. В то время как в левой части ε ₀ =0,09, термоЭДС при замедлении S _↓ имеет два пика с почти нулевым значением S _↑ .

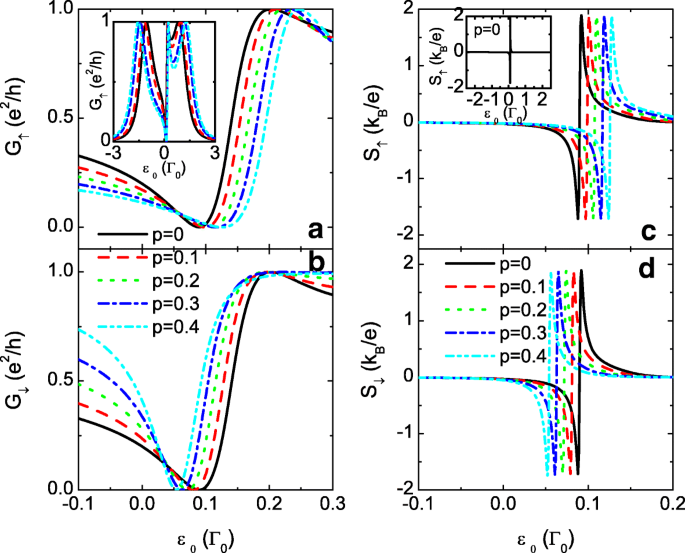
Электропроводность и термоЭДС для t ₀ =1. Спин-поляризованная проводимость G _σ через а и b , а термоЭДС S _σ в c и d как функции уровня точки ε ₀ для t ₀ =1, t _c =0,3 и различные значения спиновой поляризации межточечных взаимодействий p . Вставки в a и c - проводимость и термоэдс в режиме больших точек соответственно. Остальные параметры как на рис. 2

Другой интересный результат - это чистая спиновая термоЭДС, т.е. S _s = S _↑ - С _↓ ≠ 0, а S _e = S _↑ + S _↓ =0, или чистый спиновый ток в замкнутой цепи при конечном тепловом смещении [58]. Это означает, что ускоряющие и замедляющие термоэдс равной величины имеют противоположные знаки. Величина S _s максимизируется, когда острые пики в термоЭДС со вращением вниз и вверх с противоположными знаками встречаются на одном и том же ε ₀ регулируя спин-поляризацию межточечных связей p . Как показано на рис. 6a, нулевые точки, а также пики в S _↑ и S _↓ сдвинуты соответственно в правую и левую части ε ₀ =90 тыс. _B Т из-за p ≠ 0. В результате отрицательный пик термоэдс со спином вверх и положительный пик термоэдс со спином вниз возникают одновременно около ε ₀ =90 тыс. _B Т индуцирование чистой спиновой термоЭДС. Обычно это происходит при малых p потому что два узких пика в S _σ очень близки к нулевым точкам, что подтверждается синей штрихпунктирной линией на рис. 6а с p =0,02. Чтобы ясно показать доминанту малой энергии, мы выбираем k _B Т как единица энергии в нем. Подчеркнем, что эта чистая спиновая термоэдс может быть получена с очень малой спиновой поляризацией межточечной связи, которая реализуется путем приложения слабого магнитного поля к туннельным барьерам. Кроме того, величина чистой спиновой термоЭДС равна зарядовой (зеленая пунктирная линия).

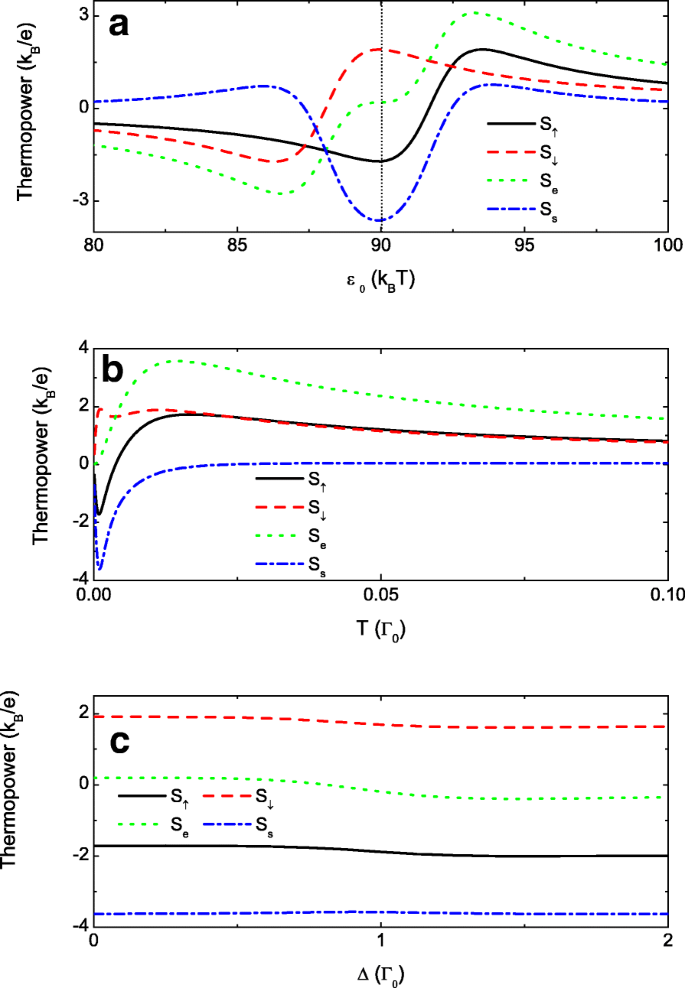
Квантовые регуляторы термоэдс. Термоэлектрические характеристики меняются в зависимости от уровня точки в a , температура в b и отстройка уровня в c . Остальные параметры: p =0,02, t ₀ =1 и t _c =0,3. Уровень точки в b и c выбрано как ε ₀ =0,09 Γ ₀ . Отстройка уровня Δ =0 в a и b , а температура составляет T =0,001 дюйма a и c

Наконец, мы представляем спиновое разрешение, чистый спин и термоЭДС, меняющиеся в зависимости от температуры T и отстройка уровня Δ на рис. 6б и г соответственно. Уровень точки ε ₀ выбрано 0,09, чтобы сфокусироваться на антирезонансной долине Фано. На рисунке 6b показано, что при низкой температуре S _↑ и S _↓ появляются пики с противоположными знаками, обозначенные сплошными и пунктирными линиями, что приводит к довольно большой чистой спиновой термоЭДС S _s (синяя штрихпунктирная линия). Теперь заряд термоЭДС S _e может быть очень маленьким, как показано зеленой пунктирной линией. С повышением температуры эффект Фано разрушается из-за случайного теплового движения носителей, и пики в S _σ размазаны. В результате разница между S _↑ и S _↓ неотличима, а чистая спиновая термоЭДС стремится к нулю. Рисунок 6d показывает, что чистая спиновая термоЭДС устойчива к разнице между уровнями точек Δ . Это согласуется с результатом уравнения. (7) антирезонансное состояние Фано не зависит от точек 1 и 2.

Выводы

В заключение, мы изучили свойства электропроводности и термоэдс в ТКТ, соединенных последовательно или по кругу с помощью спин-зависимых межточечных связей. Особое внимание уделено генерации 100 % спин-поляризованные и чисто спиновые термоэдс. Обнаружено, что первая может быть реализована в конфигурации последовательных ДКТ с достаточно большой спиновой поляризацией межточечного взаимодействия, когда точки достаточно сильно связаны друг с другом. Если же точки слабо связаны, гигантские 100 % Спин-поляризованная термоЭДС может быть реализована при очень малой спиновой поляризации межточечного взаимодействия. Когда точки имеют круговую конфигурацию, термоЭДС антисимметрична по отношению к состоянию антирезонанса Фано, вокруг которого термоЭДС развивает резкие пики. Изменяя спин-поляризацию межточечных взаимодействий, пики в термоэдсах со спином вверх и вниз смещаются в противоположных направлениях в режиме уровней КТ. Теперь 100 % Спин-поляризованные и чисто спиновые термоэдс могут быть реализованы довольно просто. Настоящие результаты могут быть получены при малых значениях спиновой поляризации межточечных связей, что является благоприятным для экспериментов.