Прогнозирование квантового аномального эффекта Холла в сотах MBi и MSb (M:Ti, Zr и Hf)

Фон

Строгие исследовательские усилия были постоянно сосредоточены на изучении новых 2D-материалов, таких как квантово-спиновые изоляторы Холла (QSH). Эти новые материалы, также известные как двумерные топологические изоляторы (2D ТИ), демонстрируют уникальное свойство, заключающееся в том, что края обладают спин-поляризованными бесщелевыми состояниями, несмотря на то, что объемная система является изолятором [1]. Изоляторы QSH демонстрируют бездиссипативный перенос спина / заряда, который очень важен для приложений спинтроники [2]. Недавно было обнаружено, что нарушение симметрии обращения времени (TRS) в изоляторах QSH приводит к системе квантового аномального эффекта Холла (QAHE), в которой спиральные краевые состояния преобразуются в киральные краевые состояния [3]. Бездиссипативный перенос заряда без необходимости во внешнем магнитном поле обеспечивает многообещающие применения в спинтронике с низким энергопотреблением [4, 5] и способствует поиску большего количества систем QAHE [6, 7]. Предсказанный Холдейном в 1988 г., QAHE был экспериментально достигнут только в 2013 г. путем магнитного легирования тонких пленок топологических изоляторов [8]. Теоретические исследования показали, что квантовая аномальная холловская (QAH) фаза может быть достигнута путем нарушения TRS ТИ путем введения ферромагнетизма и индуцирования перехода с инверсией зон за счет эффектов сильной спин-орбитальной связи (SOC) [9, 10]. Таким образом, изоляторы QSH являются хорошими исходными материалами для достижения QAHE. В нескольких исследованиях было предсказано, что тонкие пленки групп IV (Sn) [11–13] и V (Bi, Sb) [6, 14–17] поддерживают фазы QSH, которые также могут быть получены с помощью химической функционализации [17, 18]. Помимо элементов IV и V групп, было также предсказано, что [19–21] соты III-V поддерживают фазу QSH как в автономных, так и в функционализированных случаях. Эти результаты проложили путь к поиску фаз QAHE. Исследования показали, что QAHE существует в функционализированных тонких пленках групп IV [22] и V [17, 18, 22]. Кроме того, расчеты из первых принципов показывают QAHE во фторированных [23] и химически функционализированных [24] сотах III-V. Более того, в нескольких теоретических исследованиях было предсказано, что легирование переходных металлов в соты может индуцировать фазы QAH [17, 25–27]. Это было экспериментально реализовано с помощью легирования Cr и V [8, 28, 29]. Подтверждая открытие, что сотовые материалы III-V являются изоляторами QSH [19], и теоретическое предсказание, что легирование магнитного материала может вызвать магнетизм [10], мы заменяем элемент III группы переходным металлом (M =Ti, Zr и Hf). Карбиды переходных металлов MC (M =Zr и Hf) [30] и галогениды переходных металлов MX (M =Zr и Hf) [31] также являются еще одним семейством материалов, которые, по прогнозам, будут существовать в качестве изоляторов QSH. Однако его потенциал для поддержки QAHE еще не исследован. На основании этих результатов мы предсказываем электронные свойства пниктидов переходных металлов MPn (M =Ti, Zr и Hf; Pn =Sb и Bi) для проявления фазы QAH. В этой работе мы используем расчеты из первых принципов, чтобы предсказать способность переходных металлов (M =Ti, Zr и Hf) индуцировать собственный магнетизм в сотах из Bi / Sb. Мы исследуем как изогнутые, так и плоские случаи и определяем фазовые изменения из-за деформации. Фазы QAH проверяются путем вычисления числа Черна и инверсии полосы наблюдения.

Результаты и обсуждения

Подобно сотам из чистого Bi (с двумя атомами в элементарной ячейке), которые могут иметь как изогнутую, так и плоскую структуру, наш материал получается путем замены половины Bi переходным металлом [например, Ti, Zr и Hf] в элементарной ячейке. . Вид сверху M-Bi / Sb с очерченной элементарной ячейкой 1 × 1 показан на рис. 1a, а виды сбоку изогнутых и плоских сот из M-Bi / Sb показаны на рис. 1b, c, соответственно. Соответствующая первая зона Бриллюэна (ЗБ), помеченная точками высокой симметрии, показана на рис. 1d.

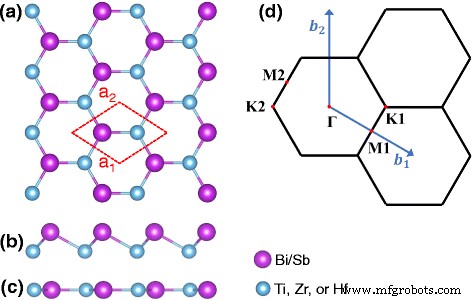
а Кристаллическая структура сот M-Sb / Bi. б , c Виды сбоку на гнутые и плоские конструкции соответственно. г Первая зона Бриллюэна (ЗБ) с точками высокой симметрии

Мы изучаем стабильность сот и влияние деформации, варьируя постоянную решетки и позволяя атомам расслабиться как для изогнутых, так и для плоских случаев. Затем мы идентифицировали их топологические фазы при различных деформациях с помощью вычислений числа Черна. Результат иллюстрируется фазовой диаграммой, представленной на рис. 2. Кривые энергии для TiBi, ZrBi и HfBi показаны на рис. 2a-c соответственно. Мы обнаружили, что соты MBi обладают малой выпуклостью и плоской фазой. С помощью этих рисунков мы идентифицируем константы равновесной решетки для дальнейшего анализа. На рисунке также показано, что изогнутый MBi является энергетически предпочтительной структурой. Однако большинство фаз QAH наблюдается при увеличении деформации, которая превращает материал из гнутого в плоские соты. Следует также отметить, что фазы QAH можно было наблюдать в выпученном HfBi, но только в небольшом диапазоне постоянных решетки [см. Рис. 2c].

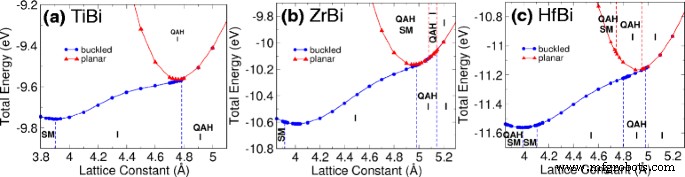
Фазовая диаграмма а TiBi, b ZrBi и c HfBi показывает полную энергию при различных постоянных решетки. Диаграмма разделена на различные области, обозначенные как QAH (квантовая аномальная холловская фаза), I (изолятор) и SM (полуметалл). Синие кружки и красные треугольники представляют изогнутый и плоский случаи соответственно

Таблицы 1 и 2 показывают равновесные постоянные решетки для структур M-Bi и M-Sb. Также указаны соответствующая запрещенная зона, магнитный момент, фаза и классификация материалов. QAHE присутствует, когда вычисленное число Черна, C, является ненулевым целым числом. Ширина запрещенной зоны рассчитывается как разница между самой низкой незанятой и самой высокой занятой полосами. Наши расчеты показывают, что фаза изолятора QAH может быть найдена в планарных TiBi и HfBi с шириной запрещенной зоны 15 и 7 мэВ соответственно. Более того, фазовый переход может быть вызван в TiBi, изменяя расстояние потери устойчивости [см. Рис. 3] и вызывая деформацию в изогнутом HfBi [рис. 4]. В TiBi мы обнаружили, что пересечение полос из-за изменения расстояния потери устойчивости происходит в точках с низкой симметрией, показанных на рис. 3d; в то время как в HfBi мы наблюдали два пересечения зон (критические точки перехода) сначала на K2 ( a =4.8 Å), а затем при K1 ( a =5,0 Å) из-за деформации на рис. 4в, ж.

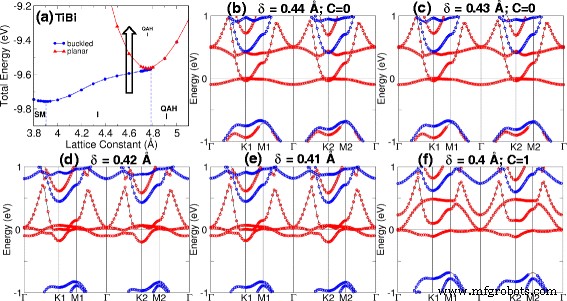
Фазовый переход после изменения длины изгиба. а Фазовая диаграмма TiBi на a =4,6 Å. Стрелка показывает путь перехода. б - е Переход ленточной структуры как расстояние потери устойчивости ( δ ) уменьшилось с 0,44 до 0,4 Å. Переход происходит при δ =0,41 Å

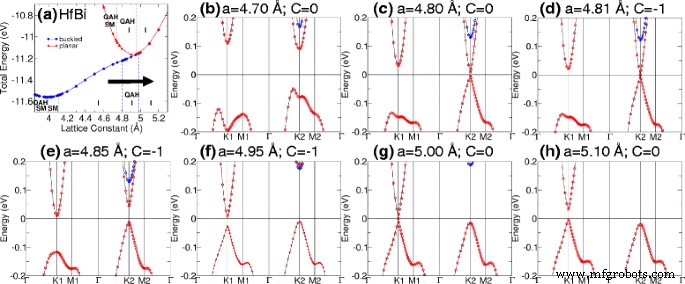
Фазовый переход после изменения постоянной решетки. а Фазовая диаграмма изогнутого HfBi. Стрелка показывает путь перехода. б - ч Переход зонной структуры при увеличении постоянной решетки с 4,7 до 5,1 Å

На рис. 5a, b показаны электронные зонные структуры при равновесных постоянных решетки для M-Bi и M-Sb в планарной и выпученной структурах соответственно. Красные и синие кружки - это вклады увеличения и уменьшения вращения соответственно. Этап QAH (с C =1) с наибольшей шириной запрещенной зоны составляет 15 мэВ, наблюдаемую в плоском TiBi. Planar HfBi также является изолятором QAH с небольшой шириной запрещенной зоны 7 мэВ (с C =−1). Однако в изогнутой форме HfBi представляет собой полуметалл с высоким C =−3. С другой стороны, изогнутые ZrBi, TiSb, ZrSb и ​​планарный ZrSb оказались тривиальными изоляторами.

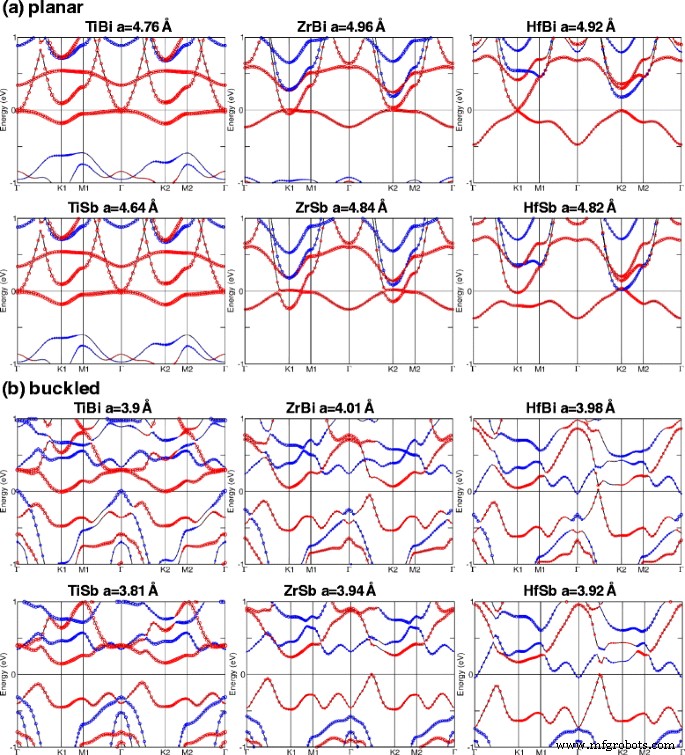
Электронные зонные структуры M-Pn (M =Ti, Zr и Hf; Pn =Sb и Bi) при их равновесных постоянных решетки для a планарный и b чехлы с пряжками. Равновесные постоянные решетки указаны над зонной структурой. Красные и синие круги обозначают + s _z и - s _z взносы соответственно

Природу QAHE можно понять, изучив эффекты SOC в немагнитных и ферромагнитных расчетах. Для этого мы выбрали планарный TiBi (с a =4,76 Å) в качестве образца. Зонные структуры, полученные в немагнитных и ферромагнитных расчетах с SOC и без него, показаны на рис. 6. Наши расчеты показывают, что эта структура имеет магнитный момент 1,05 μ _B на элементарную ячейку, который в основном вносят атомы Ti. В немагнитных расчетах мы находим, что система металлическая [рис. 6а, в]. На рис. 6b можно наблюдать, что суммарный магнитный момент может быть индуцирован из-за ферромагнитного упорядочения, на которое влияет переходный металл Ti. Кроме того, теперь система имеет бесщелевые состояния со спином вверх (красные линии) и состояния со спином вниз с щелью, и, применяя SOC к ферромагнитному расчету, затем получается щель в 15 мэВ. Это показывает, что инверсия полосы вызвана SOC, а открытие промежутка приводит к QAHE.

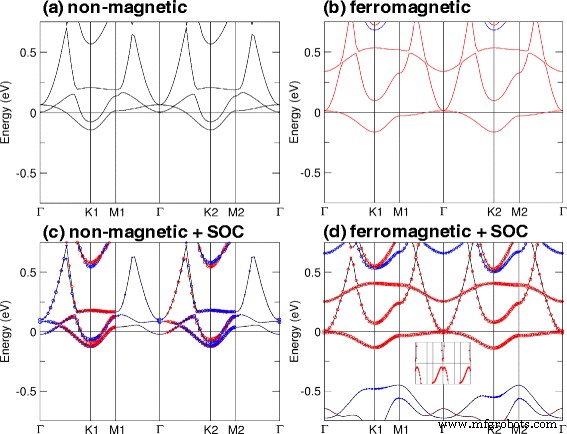
Электронные зонные структуры планарной пленки TiBi на a =4,76 Å для немагнитных расчетов ( a ) без SOC и ( c ) с помощью SOC, а также ферромагнитные расчеты ( b ) без SOC и ( d ) с SOC. Красные и синие круги обозначают + s _z и - s _z взносы, соответственно, для ( c ) немагнитный ( d ферромагнетик) расчеты с SOC

Наконец, мы проверяем спектр краевой полосы плоских сот HfBi на наличие краевых состояний, используя гамильтонианы сильной связи, полученные с помощью функций Ванье. Мы построили ленты HfBi с зигзагообразными краями и шириной 127 Å, как показано на рис. 7. Рисунок также подтверждает наличие краевых состояний, обозначенных и пропорциональных размеру красных и синих кружков, которые представляют правый и левый края, соответственно. . Раздельные краевые состояния возникают из-за асимметрии правого и левого зигзагообразных краев. Мы также можем наблюдать нечетное количество краевых полос, пересекающих уровень Ферми. Мы обнаружили, что это число совпадает с абсолютным значением числа Черна, что дополнительно подтверждает фазу QAH в планарном HfBi.

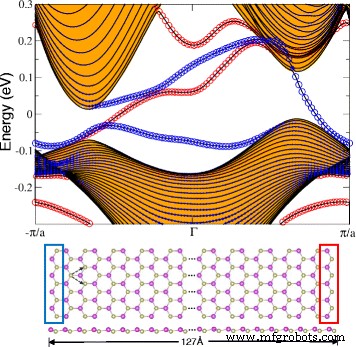
Ленточная структура вдоль края изогнутой зигзагообразной наноленты HfBi с a =4,9 Å и шириной 127 Å. Синие (красные) кружки показывают вклад левого (правого) края. Объемные полосы обозначаются оранжевой заливкой

Далее мы рассчитали фононный спектр для каждой системы и отметили, что эти системы обладают отрицательной частотой. Таким образом, вышеупомянутым системам потребуется подложка для стабилизации. Мы также отметили, что вышеупомянутые расчеты были выполнены с использованием одной за одной элементарной ячейкой, и материалы с ферромагнитной (FM) конфигурацией являются наиболее стабильным состоянием. Однако для более крупной сверхъячейки мы обнаружили, что FM по-прежнему имеет более низкую энергию, чем антиферромагнитная (AFM) конфигурация в изогнутых случаях, в то время как как FM-, так и AFM-конфигурации вырождены по энергии в плоских случаях.

Выводы

Подводя итог, наши расчеты из первых принципов предсказывают, что замена переходных металлов (Ti, Zr и Hf) на сотовые пленки Sb или Bi потенциально может привести к появлению фазы QAH. Хотя эти материалы энергетически более стабильны в изогнутой форме, преобразование их в плоскую форму дает фазу QAH в вполне разумном диапазоне постоянных решетки. Такая фаза также может быть вызвана изменением расстояния потери устойчивости и приложением деформации, как и должно быть в наших расчетных фазовых диаграммах. Мы обнаружили, что планарные структуры TiBi и HfBi существуют как QAH-изоляторы с шириной запрещенной зоны 15 и 7 мэВ соответственно. Эти открытия предлагают еще один способ реализации фазы QAH в сотовых материалах, которые потенциально могут быть использованы в спинтронных приложениях.

Методы / экспериментальные

Расчеты из первых принципов в рамках теории функционала плотности (DFT) были выполнены с использованием приближения обобщенного градиента (GGA) [32–36] и метода расширенной волны (PAW) [37], реализованного в Vienna Ab-Initio Simulation. Версия пакета 5.3 (VASP) [38, 39]. Ограничение кинетической энергии было установлено на 350 эВ, и кристаллические структуры были оптимизированы до тех пор, пока остаточные силы не стали больше 5 × 10 ⁻³ . эВ / Å. Критерии самосогласованности для сходимости были установлены на уровне 10 ⁻⁶ . эВ для расчета электронной структуры со спин-орбитальной связью или без нее. Мы моделируем тонкую пленку, вставляя вакуумный слой толщиной не менее 20 Å вдоль z направление на выбранной двумерной зоне Бриллюэна гамма-центрированных сеток Монкхорста-Пак размером 24 × 24 × 1 [40]. Мы рассчитали максимально локализованные функции Ванье с помощью пакета WANNIER90 [41], которые затем использовались для вычисления краевых состояний. Топологические фазы были идентифицированы путем вычисления числа Черна с помощью пакета Z2Pack [42, 43], в котором используется методика отслеживания гибридных центров заряда Ванье.