Чрезвычайно улучшенный отклик фототока в нанолистах топологического изолятора с высокой проводимостью

Введение

Постоянно идет поиск материалов с более высокой чувствительностью к фототоку. Малая глубина проникновения света в твердотельные материалы приводит к тому, что в отклике фототока преобладают поверхностные носители. Материал с более высоким содержанием поверхностных носителей является лучшим кандидатом в качестве фотодетектора. В течение долгого времени широко изучались материалы с высоким отношением поверхности к объему, такие как нанопроволоки [1–6]. Наряду с широкой полосой фотодетектирования низкоразмерные материалы с линейной ЭК-дисперсией, такие как графен, [7, 8] гетероструктуры на основе графена [1–4], двумерные дихалькогениды переходных металлов (ДПМ) и топологические материалы, привлекли широкое внимание [9–16].

Недавние сообщения показывают, что заявленный отклик фототока варьируется в широких пределах [17–22]. Эти распределения можно интуитивно приписать разным условиям роста материала и экспериментам. В большинстве отчетов основное внимание уделяется корректировке компонентов материала. Возможные внутренние механизмы этих распределений менее изучены и обсуждаются. Уточнение внутреннего механизма может помочь устранить потенциальный дефект и значительно оптимизировать производительность. Считается, что качество образца должно быть решающим фактором, определяющим отклик фототока [17–22]. Существуют ли какие-либо другие простые физические методы, помимо анализа кристаллической структуры и компонентов, для определения качества образца? Мы обратили внимание на то, что светочувствительность распространяется в широком диапазоне с различным сопротивлением листа на основе ряда экспериментальных отчетов. Процессы переноса электронно-дырочных пар, индуцированные фотонами, следуют за процессами рассеяния в мезоскопических твердотельных системах, поэтому проводимость материала будет решающим фактором в доминировании зарегистрированного отклика фототока. Однако этот эффект еще недостаточно изучен, и соответствующие экспериментальные работы отсутствуют.

Чтобы выявить влияние проводимости на отклик фототока, мы систематически исследовали отклик фототока в нанолистах топологического изолятора с разной проводимостью. Фототок линейно зависит от силы света, а фототок пропорционален темновому току. Более высокий фототок наблюдается в нанолисте с более высокой проводимостью. Чувствительность пропорциональна проводимости нанолиста более двух порядков. Чувствительность не зависит от силы света в вакууме, но чувствительность резко снижается при низкой интенсивности света в воздухе. Отношение чувствительности в воздухе к чувствительности в вакууме отрицательно пропорционально обратной величине силы света. Такое поведение понимается как статистический фототок в системе с заблокированными молекулами. Постоянная времени уменьшается с увеличением толщины. Такое поведение можно понять как процесс протекания тока однородности. Определены постоянные времени заряда и разряда при различных давлениях. Более длительная постоянная времени наблюдается при более низком атмосферном давлении. Отзывчивость, R , линейно зависит от проводимости нанолиста. R в V =0,1 В достигает 731 на нанолистах с более высокой проводимостью. Это выше, чем все указанные значения в (Sb, Bi) ₂ (Te, Se) ₃ топологические изоляторы и низкоразмерные материалы и только ниже, чем несколько описанных гетероструктур.

Экспериментальный метод

Монокристаллы Sb ₂ Se ₂ Те выращивали в самодельной печи с плавающей зоной с резистивным нагревом (RHFZ). Исходное сырье Sb ₂ Se ₂ Смешивали в соответствии со стехиометрическим соотношением. Сначала стехиометрические смеси высокочистых элементов Sb (99,995%), Se (99,995%) и Te (99,995%) плавили при температурах 700 ∼ 800 ° C в течение 20 ч, а затем медленно охлаждали до комнатной температуры в откачанная трубка из кварцевого стекла. Полученный материал использовали в качестве питающего стержня для следующего эксперимента RHFZ. После выращивания кристаллы охлаждали в печи до комнатной температуры. Выращенные кристаллы раскалывались вдоль базисной плоскости, создавая серебристую блестящую зеркальную поверхность, а затем готовились к дальнейшим экспериментам. Спектры комбинационного рассеяния света, EDS и XPS подтверждают, что кристалл Sb ₂ Se ₂ Te. Дифракция рентгеновских лучей показывает резкие пики, которые указывают на то, что Sb ₂ Se ₂ Кристалл имеет высокую кристалличность и однородность. Наши предыдущие работы показывают, что физические параметры, извлеченные из ARPES и квантовой осцилляции ШдГ, согласованы. Они поддерживают Sb ₂ Se ₂ Кристалл демонстрирует высокое качество и однородность.

Сб ₂ Se ₂ Нанолисты были получены расслаиванием объемных кристаллов с помощью ленты для нарезки кубиков, а затем были диспергированы на изолирующем SiO ₂ (300 нм) / n -Si шаблоны с предварительно нанесенными схемами Ti / Au. Затем на выбранный Sb ₂ были нанесены два металлических контакта из платины (Pt). Se ₂ Нанолисты с использованием метода сфокусированного ионного пучка (FIB). На рис. 1a – c показаны изображения трех Sb ₂ , полученные с помощью СЭМ. Se ₂ Нанолисты. Толщина нанолистов определена с помощью атомно-силовой микроскопии, и измеренная толщина трех синтезированных нанолистов составила 58 нм, 178 нм и 202 нм соответственно. Электропроводность этих нанолистов измерялась Keithley 4200-SCS. Сила тока измерялась как функция приложенного напряжения двухзондовым методом. Я ⁺ и V ⁺ являются той же точкой контакта, и I ^- и V ^- являются той же точкой контакта. Чтобы определить влияние собственной проводимости на отклик фототока, для измерения фототока были подготовлены три нанолиста с разной проводимостью.

а , b , и c показать SEM-изображения трех Sb ₂ Se ₂ Нанолисты. Толщина нанолиста измеряется с помощью АСМ. На нанолист наносились два Pt-контакта для измерения фототока. г , e , и f выявляют зависимость напряжения от тока, и она является линейной. Это указывает на омический контакт между платиновыми электродами и Sb ₂ Se ₂ Нанолисты

Результаты и обсуждение

На рис. 1d – f показана линейная зависимость напряжения от тока. Это указывает на металлические характеристики и омические контакты между платиновыми электродами и нанолистами. Измеренная проводимость, G , равны 4 × 10 ⁻⁵ , 0,006 и 7 × 10 ⁻⁵ (S) для нанолистов толщиной 202, 178 и 58 нм соответственно. Электропроводность выше 1000 (См / м), что обеспечивает чрезвычайно высокое качество кристаллов в наших нанолистах.

На рис. 2а – с показаны измеренные токи в зависимости от силы света. На рис. 2г – е видно, что измеренный ток пропорционален силе света [27, 28]. Отношение может быть выражено как I _на = β P ^α + Я _выкл , где I _на - измеренные токи со светом, I _выкл - измеренные токи без света, β - константа, связанная с реакцией фототока, P - сила света, а α - константа, связанная с состоянием освещения между устройствами и светом. Стоит отметить, что чем больше I _на наблюдается в нанолисте с большим I _выкл . Фототок, I _ph , определяется как I _на - Я _выкл . В таблице 1 приведены результаты подгонки. Это показывает, что α ≈1 для всех нанолистов с разной толщиной, что поддерживает согласованные оптические характеристики этих нанолистов. Стоит отметить, что β / G составляет 1,1 × 10 ⁵ ± 0,2 × 10 ⁵ (A / WS) для всех нанолистов. Это указывает на то, что наблюдаемый фототок пропорционален эффективной проводимости. Этот вывод подтверждает, что помимо геометрии системы и зонной структуры материала, эффективная проводимость нанолистов также будет критическим фактором, определяющим отклик фототока.

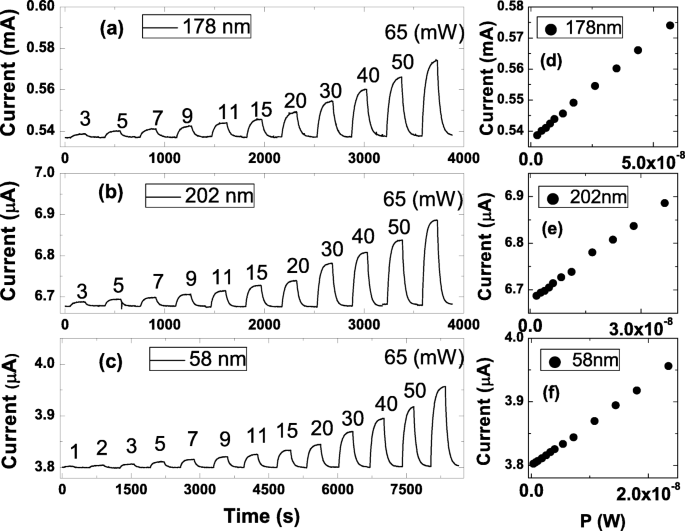
а , b , и c показать измеренные токи как функцию силы света в трех образцах разной толщины. г , e , и f показывают, что измеренные токи пропорциональны силе света. Обращаем внимание, что чем больше I _на наблюдается в нанолисте с большим I _выкл

Я _ph возникает из электронно-дырочных пар, индуцированных взаимодействием между инжектированными фотонами и нанолистами. Индуцированные электроны и дырки текут в противоположных направлениях под действием электрического смещения. Эффективный Я _ph пропорциональна приложенному напряжению и количеству электронно-дырочных пар. Больше инжектированных фотонов приводит к большему количеству электронно-дырочных пар. Глубина проникновения света небольшая и слабая в зависимости от силы света. Сообщается, что глубина проникновения света в топологических изоляторах составляет примерно 20 нм, что меньше толщины наших нанолистов [23, 24]. Я _ph не должно зависеть от толщины нанолиста, если толщина больше глубины проникновения света. Площадь поверхности нанолиста распределяется в 3 раза, но наблюдаемое значение I _ph распространяется на разницу в два порядка. Помимо эффективных индуцированных электронно-дырочных пар, наблюдаемые различные I _ph должны происходить из внутренних свойств. Чтобы исключить влияние внешней геометрии на I _ph и количественно определить характеристики этих нанолистов, чувствительность, R , рассчитывается по следующей формуле:

где P и S - сила света и эффективная площадь соответственно.

На рисунке 3 показан R . как функция силы света, отличается от того, о котором в большинстве случаев сообщалось, что R резко снижается с увеличением интенсивности света в топологических изоляторах на основе Bi и низкоразмерных материалах [25, 26]. Наши результаты показывают, что R и G не зависят от силы света в вакууме. Это также подтверждает, что глубина проникновения света должна быть меньше, чем толщина нанолиста в наших экспериментальных условиях. Чем больше R наблюдается в нанолисте с более высокой проводимостью. Это подтверждает, что наблюдаемый более высокий фотоотклик происходит из-за внутренних транспортных характеристик, а не из-за геометрии нанолиста или условий эксперимента.

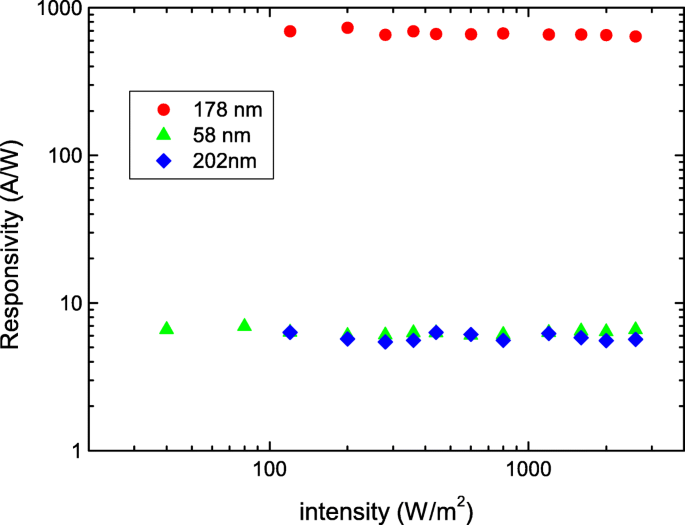
Чувствительность трех Sb ₂ Se ₂ Нанолисты. Выявлена ​​слабая зависимость силы света от чувствительности. Более высокая чувствительность наблюдается в нанолисте с более высокой проводимостью

Как показано на рис. 1, линейная зависимость напряжения от тока подтверждает, что нанолисты проявляют металлическое поведение. Индуцированные светом электронно-дырочные пары будут перемещаться к контактам двух электродов из-за приложенного напряжения смещения [27–29]. Согласно закону Ома соответствующий фототок может быть определен через соотношение I _ph = V G где V это приложенное напряжение смещения между двумя электродами. Я _ph пропорциональна G .

На рисунке 4 показан R как функция G в бревенчатом участке. Точки данных Sb ₂ Se ₂ Te - результаты измерений в этой работе, а точки данных Sb ₂ СЕТЬ ₂ взяты из нашей предыдущей работы при тех же условиях выращивания кристаллов и измерительных установках [27]. Толщина Sb ₂ СЕТЬ ₂ нанолисты имеют размер около 180 нм. Длина волны 532 нм. Оба Sb ₂ Se ₂ Те и Сб ₂ СЕТЬ ₂ показать, что R не зависит от силы света. Эти точки данных повторяют тенденцию пунктирной линии в широком диапазоне проводимости нанолиста. Это подтверждает, что R пропорциональна G , что соответствует нашему предложению.

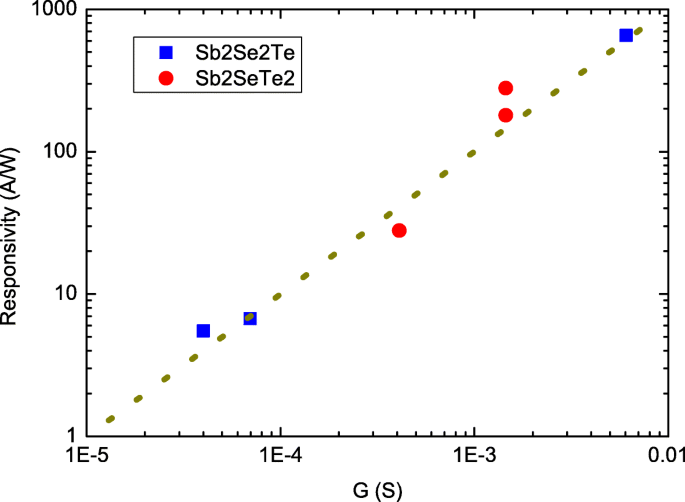
Чувствительность как функция проводимости нанолиста. Это показывает, что чувствительность пропорциональна проводимости нанолиста. Сб ₂ СЕТЬ ₂ данные взяты из наших отчетных значений

Для потенциальных приложений очень предпочтительна система с более высокой чувствительностью по фототоку. Помимо поиска новых материалов или систем с определенной структурой зон и шириной запрещенной зоны, надлежащая обработка системы также может быть подходящим методом для улучшения фотоотклика. Наши экспериментальные результаты подтверждают, что собственная электрическая проводимость будет критическим фактором для оптимизации отклика фототока. Это может быть достигнуто за счет соответствующих условий роста. Как показано на рис. 4, фототок увеличивается на 2 порядка за счет регулировки проводимости. Это исследование может помочь другим исследователям разработать подходящие рекомендации по выбору лучшей системы для дальнейших экспериментальных исследований с помощью простого электрического теста.

R и обнаруживаемость на V =0,1 В достигает 731 и 2,6 × 10 ¹⁰ на нанолисте с более высокой проводимостью. Эти фотоответы превышают все зарегистрированные значения в (Sb, Bi) ₂ (Te, Se) ₃ топологические изоляторы и низкоразмерные материалы [27, 28] и только ниже, чем несколько описанных гетероструктур. В последнее время большое внимание в области фототока привлекли низкоразмерные материалы. Мы обращаем внимание на то, что проводимость этих низкоразмерных материалов чрезвычайно высока. Это согласуется с нашим экспериментальным результатом, согласно которому проводимость является решающим фактором, определяющим отклик фототока.

На рисунке 5 изображен R как функции силы света в вакууме и атмосфере. Нашему вниманию предлагается R резко уменьшается при интенсивности света ниже 500 Вт · м ⁻² в атмосфере. Это подтверждает, что это уменьшение R при низкой интенсивности света в атмосфере может происходить из-за влияния адсорбированной молекулы на поверхности нашего Sb ₂ Se ₂ Нанолист.

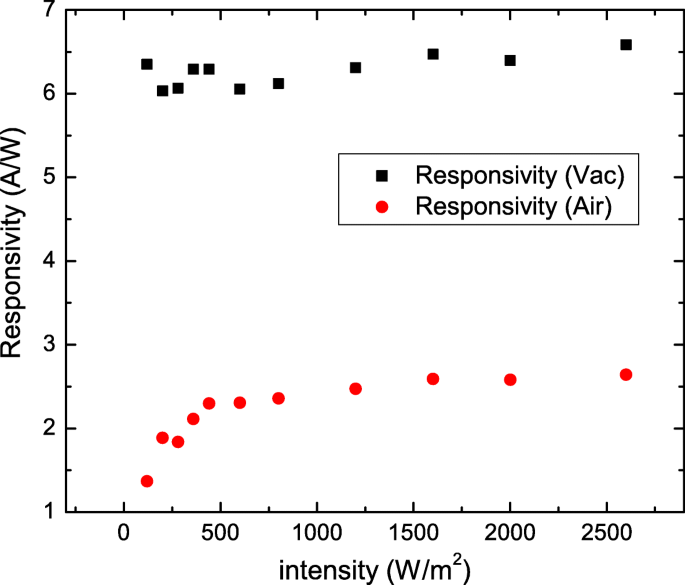
Чувствительность и коэффициент фотопроводимости как функции интенсивности света на длине волны 532 нм. Чувствительность - это слабая зависимость силы света в вакууме. Чувствительность уменьшается по мере уменьшения интенсивности света в атмосфере, когда сила света ниже 500 Вт / м ²

Фотоотклик будет чрезвычайно чувствителен к состоянию поверхности образца. Помимо уменьшения эффективной площади отклика, поверхностные дефекты и окисление могут снизить подвижность носителей и срок их службы.

Недавно сообщалось, что адсорбированные молекулы на поверхности Bi ₂ Se ₃ топологические изоляторы искривляют конструкцию и приводят к дополнительному 2DEG. Этот индуцированный 2DEG может увеличить эффективную подвижность носителей [30]. Система с более высокой подвижностью носителей может уменьшить время прохождения носителей и произвести более высокий фототок. С другой стороны, повышенная подвижность носителей не должна зависеть от интенсивности света. Они подтверждают, что наблюдаемый R подавление происходит в основном из-за эффективной светящейся площади, а не из-за внутренних транспортных характеристик. Таким образом, считается, что падение R в воздухе при низкой интенсивности света должно быть больше связано с эффектом адсорбированной молекулярной тени, чем с эффектом релаксации собственного сложного носителя.

Определение чувствительности - это отношение индуцированного носителя к падающим фотонам, и это также может быть выражено как \ (R =\ eta \ frac {q} {hf}, \), где q , hf , и η - заряд носителей, энергия фото и квантовая эффективность соответственно. η напрямую зависит от свойств материала и длины волны света. Чтобы исключить другие внешние и внутренние эффекты и оптимизировать эффект тени молекулы, R ( а я г ) / R ( v а c ) представляет собой график как функцию силы света. Как показано на рис. 6, это соотношение увеличивается по мере увеличения энергоемкости и постепенно достигает насыщения при высокой энергоемкости.

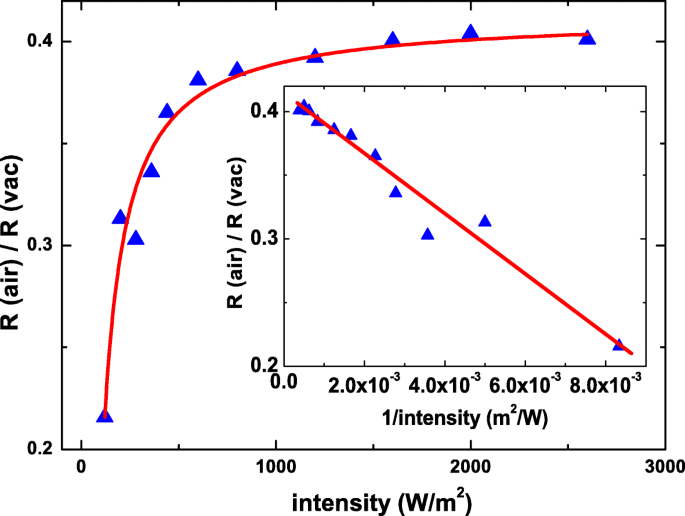
Отношение чувствительности в воздухе к чувствительности в вакууме в зависимости от силы света. Точки данных хорошо согласуются с теоретическим предположением. На вставке показано, что отношение чувствительности в воздухе к чувствительности в вакууме отрицательно пропорционально обратной величине силы света

Мы предлагаем модель, в которой число падающих фотонов равно Y , м фотоны взаимодействуют с материалом, и n фотоны блокируются адсорбированными молекулами на поверхности. То есть Y = м + н . Z - среднее число носителей фототока, индуцированных одним фотоном. При очень слабой интенсивности света число фото намного меньше, чем общая молекулярная единица, эффективный фототок должен соответствовать статистическим расчетам, и результат подтверждает, что квантовая эффективность, η , может быть выражено как

Этот статический расчет подтверждает, что эффективный фототок будет сильно зависеть от интенсивности света в пределе слабой силы света и большого времени релаксации; количество фотонов может быть меньше, чем у «создателя фотоносителя». Эффективный фототок можно выразить как

Y прямо пропорциональна силе света. R ( а я г ) / R ( v а c ) отрицательно пропорционален обратной величине Y и слабо зависит от Y в ситуации Y ≫ n . Как показано на рис. 6, он ясно показывает, что измеренные точки данных хорошо согласуются с теоретическим уравнением, а на вставке показано, что точки данных отрицательно пропорциональны обратной величине интенсивности света. Они подтверждают, что наблюдаемое падение фототока в основном связано с теневым эффектом адсорбированных молекул на поверхности. \ (\ Frac {R (воздух)} {R (vac)} \) составляет примерно 0,4 при высокой энергоемкости, и это указывает на то, что поверхность покрыта адсорбированными молекулами на 40%.

На левой нижней вставке рис. 7 показан фототок как функция времени. Процесс зарядки можно описать e ^{- t / к} , где k - характерная постоянная времени. Наш экспериментальный результат показывает, что измеренный фототок хорошо согласуется с линией подгонки. На правой верхней вставке показана постоянная времени извлеченного заряда как функция толщины. Он показывает, что постоянная времени уменьшается с увеличением толщины. Такое поведение можно понять как процесс протекания тока однородности [27, 28]. С другой стороны, определены постоянные времени заряда и разряда при различных давлениях атмосферы. Он показывает, что постоянная времени заряда примерно такая же, как постоянная времени разряда, а более длительная постоянная времени наблюдается при более низком атмосферном давлении.

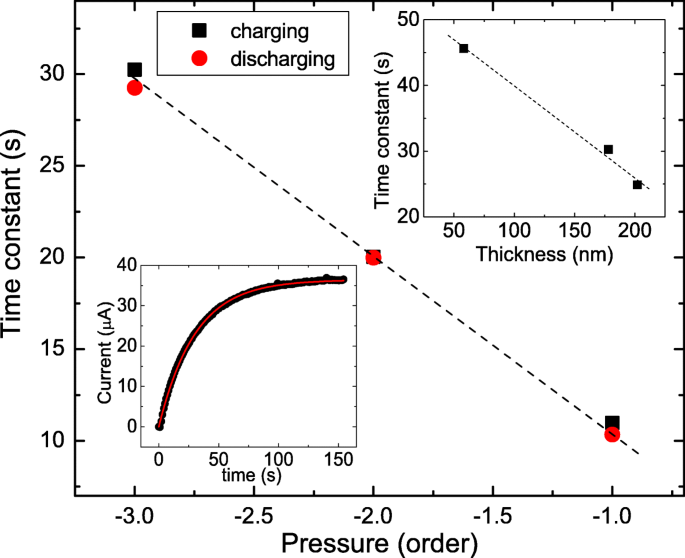
На нижней левой вставке показан фототок как функция времени в процессе зарядки, и это хорошо сочетается с линией фитинга. На правой верхней вставке показана постоянная времени заряда как функция толщины. Постоянная времени заряда и разряда как функция давления

Заключение

Фототок проводился в Sb ₂ Se ₂ Топологический изолятор с разной проводимостью на длине волны 532 нм. Фототок линейно зависит от силы света, а фототок пропорционален темновому току. Более высокий фототок наблюдается в нанолисте с более высокой проводимостью. Чувствительность пропорциональна проводимости нанолиста. Чувствительность не зависит от силы света в вакууме, но чувствительность резко снижается при низкой интенсивности в воздухе, то есть в отличие от большинства опубликованных результатов. Отношение чувствительности в воздухе к чувствительности в вакууме отрицательно пропорционально обратной величине силы света. Такое поведение понимается как статистический фототок в системе с заблокированными молекулами. Согласно теоретической модели, в воздухе поверхность покрывается адсорбированными молекулами на 40%. Постоянная времени уменьшается с увеличением толщины. Такое поведение можно понять как процесс протекания тока однородности. Определены постоянные времени заряда и разряда при различных давлениях. Более длительная постоянная времени наблюдается при более низком атмосферном давлении. R и обнаруживаемость на V =0,1 В достигает 731 и 2,6 × 10 ¹⁰ на нанолисте с более высокой проводимостью. Это выше, чем все указанные значения в (Sb, Bi) ₂ (Te, Se) ₃ топологические изоляторы и низкоразмерные материалы и только ниже, чем несколько описанных гетероструктур.

Сокращения

ARPES:

Фотоэмиссионная спектроскопия с угловым разрешением

EDS:

Энергодисперсионная рентгеновская спектроскопия

SdH:

Шубников-де Хаас

XPS:

Рентгеновская фотоэлектронная спектроскопия