Бифуркация магнитной восприимчивости в топологическом изоляторе Sb2Te3, легированном никелем, с антиферромагнитным порядком, сопровождаемым слабым ферромагнитным выравниванием

Введение

Трехмерные топологические изоляторы обладают бесщелевым поверхностным состоянием с линейной дисперсией, защищенным симметрией относительно обращения времени [1, 2]. Топологическое поверхностное состояние состоит из спин-фильтрованных фермионов Дирака. Эта спин-спиральная текстура топологического состояния поверхности привлекла большое внимание из-за ее возможных электрических и спиновых приложений [3,4,5,6,7,8,9,10,11,12,13,14 , 15,16,17,18,19,20]. Помимо присущих ему экзотических характеристик, введение намагниченности в топологический изолятор изменит электронику. Это обменное взаимодействие между электроном проводимости и магнитными атомами нарушает симметрию относительно обращения времени, что открывает разрыв в поверхностном состоянии Дирака. Фермион Дирака в поверхностном состоянии становится массивным [1, 2, 21] и приводит ко многим интересным свойствам, таким как квантовый аномальный эффект Холла, [22, 23] топологический магнитоэлектрический эффект [24], перестраиваемость киральной краевой моды [ 25, 26] и плетение Майорана [27,28,29]. Носитель из топологического поверхностного состояния доминирует над этими магнитоэлектрическими свойствами. Многие экспериментальные работы были выполнены в тонких пленках Mn, Cr и V (Bi, Sb) \ (_ {2} \) Te \ (_ {3} \), чтобы реализовать теоретические предсказания [30]. Большинство этих исследований в основном сосредоточено на электромагнето-транспортных свойствах, таких как квантовый аномальный эффект Холла, топологический магнитоэлектрический эффект и связанные с ними приложения. Из-за слабого сигнала магнетизма в тонкой пленке со слабым топологическим изолятором, легированным магнитными элементами, сообщалось о редких исследованиях внутренних магнитных свойств легированных магнитами топологических изоляторов, легированных магнитными элементами, и связанная с этим магнитная связь недостаточно изучена. Чтобы понять характерные новые физические свойства топологического изолятора, легированного магнитным элементом, особенно роль магнитного элемента и связанного с ним магнитного взаимодействия, было бы полезно точно использовать магнито-свойства в соответствующем приложении.

В данной работе исследованы магнитные свойства монокристалла топологического изолятора Sb \ (_ {2} \) Te \ (_ {3} \), легированного никелем. Петля гистерезиса с низким коэрцитивным полем наблюдалась ниже температуры Нееля (\ (T _ {\ mathrm {N}} \)). Магнитная восприимчивость показывает толчок в \ (T _ {\ mathrm {N}} \), который не зависит от внешнего магнитного поля. Магнитная восприимчивость холодных процессов с нулевым полем и холодных процессов по полю совпадают выше \ (T _ {\ mathrm {N}} \) и являются бифуркационными ниже \ (T _ {\ mathrm {N}} \). Расщепление магнитной восприимчивости больше при более низких внешних магнитных полях и температурах. При магнитном поле выше 7000 Э расщепления магнитной восприимчивости больше не наблюдается. Наше исследование подтверждает, что эти характеристики магнитной восприимчивости происходят из антиферромагнитного порядка, сопровождаемого слабым ферромагнетизмом. Извлеченная насыщенная восприимчивость хорошо согласуется с тенденцией измеренного каспа магнитной восприимчивости. Помимо большинства сообщений о том, что касп магнитной восприимчивости возникает из-за текстуры спина носителей в точке Дирака топологического состояния поверхности, наши результаты показывают, что это может быть связано с ферромагнетизмом магнитных элементов.

Экспериментальный метод

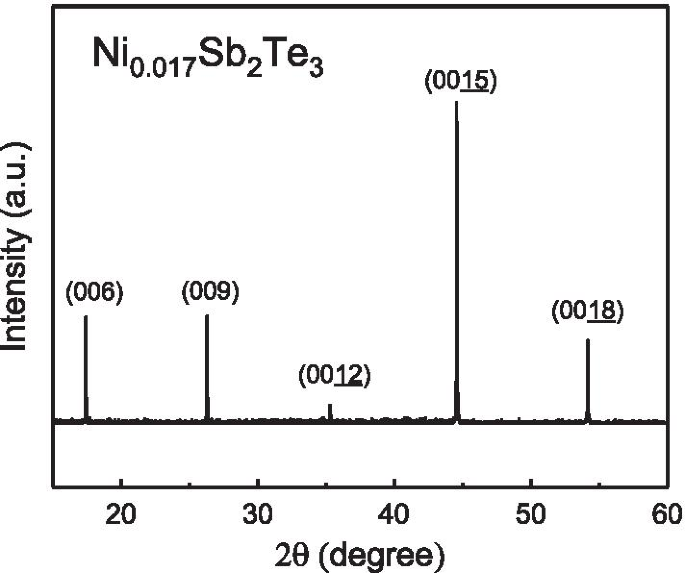
Спектр XRD монокристалла Ni \ (_ {0.016} \) Sb \ (_ {2} \) Te \ (_ {3} \). Он показывает острые пики и поддерживает структуру с высокой степенью монокристаллизации

Монокристаллы Sb \ (_ {2} \) Te \ (_ {3} \) были выращены в самодельной плавучей зонной печи с резистивным нагревом (RHFZ). Исходное сырье Sb \ (_ {2} \) Te \ (_ {3} \) смешивали в соответствии со стехиометрическим соотношением. Сначала стехиометрические смеси элементов высокой чистоты Ni (99,995%), Sb (99,995%) и Te (99,995%) плавили при \ (700 \ sim 800 ^ {\ circ} \) C в течение 20 ч, а затем медленно. охлаждали до комнатной температуры в вакуумированной трубке из кварцевого стекла. Материал был использован в качестве питающего стержня для следующего эксперимента RHFZ. Наша предыдущая работа подтверждает, что чрезвычайно высокая кристаллическая однородность в кристаллах топологического изолятора может быть получена с помощью метода RHFZ. После выращивания кристаллы охлаждали в печи до комнатной температуры. Выращенные кристаллы раскалывались вдоль базисной плоскости до серебристой блестящей зеркальной поверхности, а затем были подготовлены для дальнейших экспериментов. Результаты энергодисперсионного спектра (EDS) подтверждают, что \ (\ mathrm {Ni}:\ mathrm {Sb}:\ mathrm {Te} =0,017:2:3 \). На рисунке 1 показан спектр рентгеновской дифракции (XRD). Он показывает острые пики, и эти пики согласуются с базой данных Sb \ (_ {2} \) Te \ (_ {3} \). Это подтверждает, что наш образец сильно кристаллизован. Ожидается, что атомы Ni будут равномерно и беспорядочно распределены в монокристалле. Размер кристалла составляет 3 мм в длину, 2 мм в ширину и 0,42 мм в толщину. Измерения магнетизма проводились с использованием стандартной методики в коммерческом приборе (Quantum Design MPMS) с магнитным полем до 7 Т. Магнитное поле прикладывалось перпендикулярно к большой поверхности скола.

Результаты и обсуждение

На рис. 2 показана зависимость намагниченности от магнитных полей при различных температурах и выявлена ​​диамагнитная характеристика в широком диапазоне магнитных полей и температур. Этот диамагнетизм возникает из-за спина носителей заряда и согласуется с предыдущими сообщениями о топологических изоляторах BSTS [31]. Как показано на правой верхней вставке, в отличие от предыдущих отчетов, петля гистерезиса наблюдалась при температурах ниже 125 К. Коэрцитивное поле петли гистерезиса показывает слабую температурную зависимость и составляет примерно 50 Э. Остаточная и насыщенная намагниченность петли гистерезиса составляет примерно \ (10 ​​^ {- 5} \) emu / g и \ (10 ​​^ {- 4} \) emu / g при 100 K. Низкое коэрцитивное поле, небольшая остаточная , а небольшая насыщенная намагниченность указывает на слабый ферромагнетизм. Как показано на вставке внизу слева, четких петель гистерезиса не наблюдалось при температурах выше 125 К. Ферромагнетизм возникает из-за совмещенных магнитных моментов магнитных элементов. Тепловая энергия может хаотизировать выровненный магнитный момент и размывать ферромагнетизм выше критической температуры. Наше наблюдение показывает, что в системе наблюдается переход слабого ферромагнетизма около 120 К.

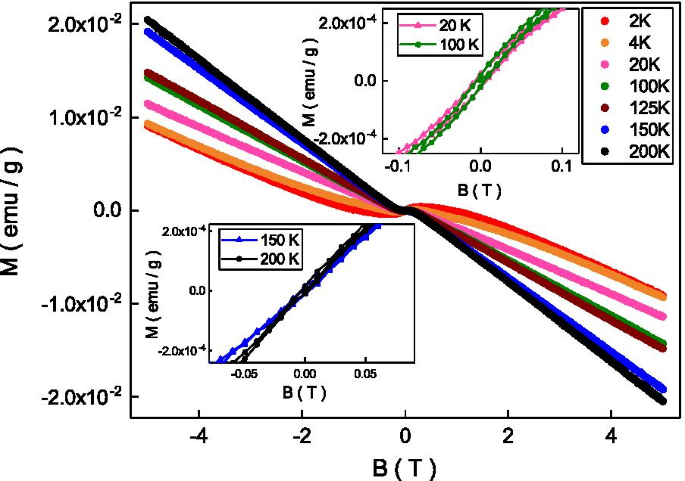
Восприимчивость как функция магнитных полей от 2 до 200 К. Выявляет диамагнетизм в сильных магнитных полях. Вставка вверху справа:петля гистерезиса наблюдалась при температуре ниже 125 К. Вставка внизу слева:петля гистерезиса не наблюдалась при температуре выше 125 К.

Чтобы исследовать собственный магнетизм, характерный для наблюдаемого слабого ферромагнитного перехода, определение магнитной восприимчивости, зависящей от температуры, проводилось с помощью процессов с полевым охлаждением и охлаждением в нулевом поле. На рис. 3 показана магнитная восприимчивость процессов с полевым охлаждением и охлаждением в нулевом поле при различных внешних магнитных полях. Магнитная восприимчивость увеличивается с понижением температуры. Он показывает разрыв при 125 К (\ (T _ {\ mathrm {N}} \)) и \ (T _ {\ mathrm {N}} \) не зависит от внешних магнитных полей. \ (T _ {\ mathrm {N}} \) - это температура Нееля, и подробный механизм будет обсужден и пояснен ниже. Магнитная восприимчивость охлаждаемых полем и нулевых полей совпадает выше \ (T _ {\ mathrm {N}} \) и раздваивается ниже \ (T _ {\ mathrm {N}} \). Большее расщепление магнитной восприимчивости наблюдается при меньших внешних магнитных полях. Наш экспериментальный результат показывает, что этот разрыв и расщепление магнитной восприимчивости больше не наблюдается при магнитном поле выше 7000 Э. Следует отметить, что флуктуация сигнала при магнитном поле 50 Э, очевидно, больше, чем в других магнитных полях. Одна из возможных причин заключается в том, что выравнивание магнитного момента является метастабильным при 50 Э, что близко к коэрцитивному полю петли гистерезиса. Как показано на рис. 2, петля гистерезиса наблюдалась только ниже 125 К, что совпадает с критической температурой бифуркации магнитной восприимчивости на рис. 3. Это указывает на то, что наблюдаемое расщепление магнитной восприимчивости может быть связано со слабым ферромагнетиком ниже температуры \ (Т _ {\ mathrm {N}} \). Известно, что ферромагнитный эффект будет размыт тепловой энергией, а магнитная восприимчивость выше критической температуры может быть описана законом Кюри-Вейсса:\ (\ chi =\ chi _ {0} + \ frac {C} { T- \ theta} \), где \ (\ chi \) - измеренная магнитная восприимчивость, \ (\ chi _ {0} \) - магнитная восприимчивость при 0 K, C - постоянная Кюри, соответствующая магнетону Бора, T - температура, а \ (\ theta \) - температура Кюри [32]. На вставке к рис. 4 показана температурная зависимость охлаждаемого в нулевом поле \ (\ frac {1} {\ chi - \ chi _ {0}} \) при различных внешних магнитных полях. \ (\ Frac {1} {\ chi - \ chi _ {0}} \) пропорционален температуре от 125 до 250 K, и наклон больше при более низких внешних магнитных полях. Наклон связан с постоянной Кюри. Линейная экстраполяция \ (\ frac {1} {\ chi - \ chi _ {0}} \) между 125 и 250 K всех внешних магнитных полей совпадают при -125 K. Согласно закону Кюри-Вейсса, это значение соответствует \ (\ theta \). Отрицательное значение \ (\ theta \) (-125 K) указывает на то, что это антиферромагнитная система ниже \ (T _ {\ mathrm {N}} \) и \ (T _ {\ mathrm {N}} \) известна как Температура Нееля [33]. Абсолютное значение \ (\ theta \) согласуется с наблюдаемым \ (T _ {\ mathrm {N}} \) на рис. 3, а критическая температура для наблюдения петли гистерезиса (125 K) на рис. Эти наблюдения показывают, что слабый ферромагнетизм и антиферромагнетизм сосуществуют ниже \ (T _ {\ mathrm {N}} \).

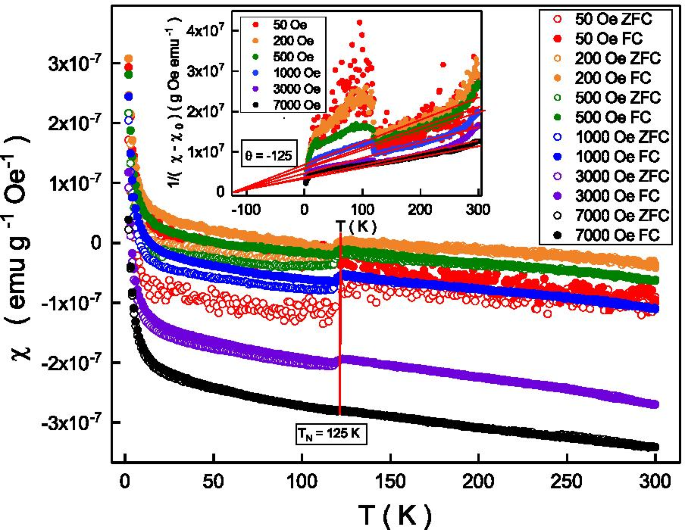
Магнитная восприимчивость охлаждаемых полем и нулевых процессов при различных внешних магнитных полях. Магнитная восприимчивость охлаждаемых полем и охлаждаемых в нулевом поле устройств совпадает выше 125 К и раздваивается ниже 125 К. Большее расщепление магнитной восприимчивости при более низких внешних магнитных полях и температурах. При магнитном поле выше 7000 Э расщепления магнитной восприимчивости больше не наблюдается. Вставка вверху справа:магнитная восприимчивость соответствует закону Кюри-Вейсса

Как показано на вставке к рис. 3, постоянная Кюри C , больше в более сильных магнитных полях. Следуя парамагнитной функции Ланжевена, C может быть выражено как \ (C =\ frac {N \ mu _ {0} \ mu ^ {2}} {3k _ {\ mathrm {B}} T} \), где N - количество магнитных элементов на единицу грамма, \ (\ mu \) - эффективный момент магнитного элемента, \ (\ mu _ {0} \) - проницаемость вакуума и \ (k _ {\ mathrm {B}} \) - постоянная Больцмана [34]. Расчетное значение \ (\ mu \) при 200 э.э. составляет около 3,5 \ (\ mu _ {\ mathrm {B}} \), что близко к теоретическому значению 3,32 \ (\ mu _ {\ mathrm {B}} \ ) [35]. Это подтверждает, что поведение магнетизма можно объяснить законом Кюри-Вейсса.

Магнитный момент случайно замораживается в холода без поля и замораживается вдоль направления внешнего магнитного поля в холода поля. Бифуркация магнитной восприимчивости возникает из-за магнитной анизотропии. Эта особенность может быть характерной для порядка антиферромагнетизма, сопровождаемого слабым ферромагнетизмом; ферромагнитные моменты доменов замерзают в случайном направлении в холодном нулевом поле, в то время как они вынуждены выравниваться вдоль приложенного магнитного поля при охлаждении поперек \ (T _ {\ mathrm {N}} \) в холодном поле [36]. Как обсуждалось выше, он состоит из слабых ферромагнитных и антиферромагнитных характеристик ниже \ (T _ {\ mathrm {N}} \) в нашей системе. Слабое ферромагнитное выравнивание могло бы немного нарушить порядок антиферромагнетизма и вызвать магнитную анизотропию. Под бифуркацией магнитной восприимчивости можно понимать слабый ферромагнетизм в антиферромагнитной системе. Эти результаты подтверждают, что наблюдаемая бифуркация магнитной восприимчивости ниже 125 К является магнитной характеристикой слабого ферромагнетизма в антиферромагнитной системе. Различное расщепление восприимчивости при разном внешнем магнитном поле может происходить из-за разного уровня парциальной поляризации антиферромагнетизма во внешних магнитных полях.

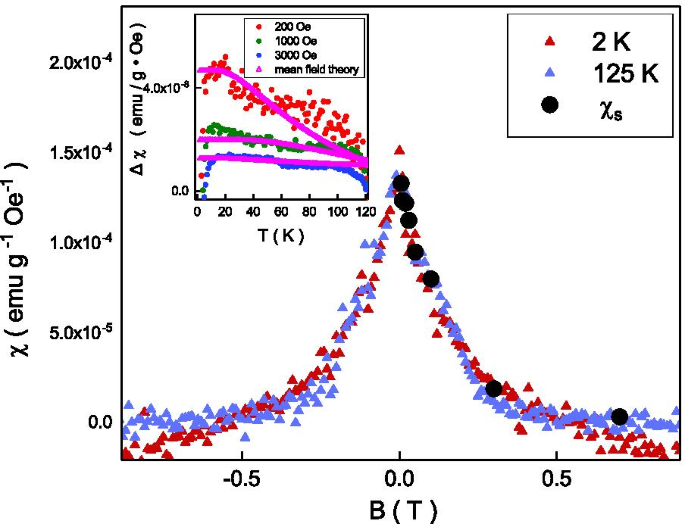
Верхняя левая вставка:разница магнитной восприимчивости охлаждаемого поля и охлаждения в нулевом поле соответствует теории среднего поля. Извлеченная насыщенная восприимчивость хорошо согласуется с тенденцией измеренного каспа магнитной восприимчивости

Следуя теории среднего поля, [37] \ (T _ {\ mathrm {N}} \) связано с силой обменной связи, \ (J_ {0} \), и его можно выразить как \ (T _ {\ mathrm {N}} =\ frac {S (S + 1)} {3k _ {\ mathrm {B}} T} J_ {0} \), где S - спиновой момент, \ (k _ {\ mathrm {B}} \) - постоянная Больцмана. \ (J_ {0} \) переходит в \ (4.28 \ times 10 ^ {22} \) джоуль в нашей системе с \ (T _ {\ mathrm {N}} \) =125 К. Теория среднего поля поддерживает что намагниченность связана с тепловой энергией в \ (e ^ {\ frac {-J_ {0} S} {k _ {\ mathrm {B}} T}} \). Магнитная восприимчивость может быть выражена как \ (\ chi =\ chi _ {\ mathrm {S}} (1-e ^ {\ frac {-J_ {0} S} {k _ {\ mathrm {B}} T}} ) \), где \ (\ chi _ {\ mathrm {S}} \) - насыщенная магнитная восприимчивость. Расщепление магнитной восприимчивости \ (\ chi _ {\ mathrm {FC}} - \ chi _ {\ mathrm {ZFC}} \) может быть выражено как \ (\ chi _ {\ mathrm {S}} e ^ {\ frac {-J_ {0} S} {k _ {\ mathrm {B}} T}} \). \ (\ Chi _ {\ mathrm {S}} \) чувствителен к внешним магнитным полям. Как показано на вставке к рис. 4, это уравнение может хорошо объяснить наш экспериментальный результат в широком диапазоне температур и внешних магнитных полей. Извлеченный \ (\ chi _ {\ mathrm {S}} \) является функцией внешних магнитных полей. Для дальнейшего изучения результата, зависимость восприимчивости от магнитного поля выполняется при температурах ниже \ (T _ {\ mathrm {N}} \), и на ней виден излом при нулевых магнитных полях. Этот пик магнитной восприимчивости при нулевом магнитном поле широко наблюдается в топологических материалах, и предполагается, что он возникает из-за текстуры спина со свободным выравниванием в точке Дирака [38]. Фотоэмиссионная спектроскопия с угловым разрешением (ARPES) показывает, что уровень Ферми находится ниже точки Дирака в нашем Sb \ (_ {2} \) Te \ (_ {3} \) [39]. Наблюдаемый касп не должен происходить из спиновой текстуры в точке Дирака. С другой стороны, коэрцитивное поле петли гистерезиса составляет около 50 Э, что на два порядка меньше полной ширины на половине максимума каспа, 0,4 Тл, и петля гистерезиса не должна быть основным источником наблюдаемого каспа. . Как показано на вставке к рис. 4, извлеченная зависимость от магнитного поля \ (\ chi _ {\ mathrm {S}} \) следует той же тенденции магнитного поля, что и измеренная магнитная восприимчивость. Это указывает на то, что широко наблюдаемый острие восприимчивости может происходить из антиферромагнитного порядка, сопровождаемого слабым выравниванием ферромагнетизма.

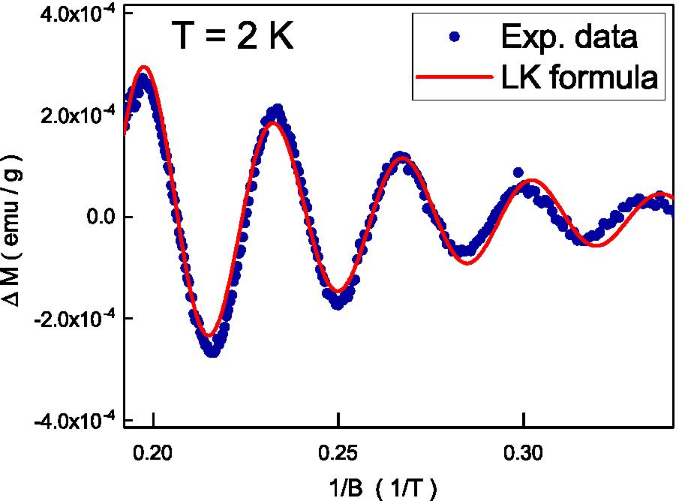
Колебания dHvA как функция обратных магнитных полей. Результат эксперимента хорошо согласуется с теоретическим уравнением

Согласно анализу, бифуркация восприимчивости возникает из-за магнетизма слабого порядка ферромагнетизма, сопровождаемого антиферромагнетизмом. Расщепление магнитной восприимчивости связано с магнитокристаллической анизотропией. При этом мы дополнительно оцениваем энергию магнитокристаллической анизотропии \ (\ Delta E =\ frac {M _ {\ mathrm {S}} H _ {\ mathrm {C}} V} {2} \), где \ (H _ {\ mathrm {C}} =50 \) э, \ (M _ {\ mathrm {S}} =1.81 \ times 10 ^ {- 11} \) J / T и \ (V =2.5 \ times 10 ^ {- 9} \ ) m \ (^ {3} \) в нашей системе и \ (\ Delta E \ sim 1.13 \ times 10 ^ {22} \) Джоуль [40]. Следуя энергии магнитного момента, \ (g \ mu _ {\ mathrm {B}} B \), можно было бы оценить, что энергия магнитокристаллической анизотропии будет ниже, чем энергия магнитного момента при \ (B> 0,61 \) Тл. Это согласуется с нашим наблюдением, что расщепление магнитной восприимчивости больше не наблюдается при внешних магнитных полях выше 0,7 Тл.

На рисунке 5 показана зависимость магнитной восприимчивости от 1 / B . и показывает периодические колебания. Это известно как осцилляции эффекта Де Гааза-Ван Альфена (dHvA), которые возникают из-за орбитального движения странствующего электрона в сильных магнитных полях [41]. Мы анализируем колебания dHvA, подгоняя колебательную намагниченность к формуле Лифшица-Косевича (ЛК) [42], \ (\ Delta M \ propto -R \ sin [2 \ pi (\ frac {F} {B} - \ delta _{п})]\). R связано со скоростью рассеяния носителей заряда, эффектом Зеемана и уширением уровней Ландау [43]. Колебания описываются синусоидальным членом, который содержит фазовый коэффициент \ (\ delta _ {p} \). \ (\ delta _ {p} \) относится к фазе Берри (\ (\ Phi _ {B} \)), \ (\ delta _ {p} =\ frac {1} {2} - \ frac { \ Phi _ {B}} {2 \ pi} \). Размер кармана Ферми характеризует значение \ (\ delta _ {p} \). Как показано на рис. 5, теоретическое уравнение хорошо согласуется с нашим экспериментальным результатом и извлеченными значениями \ (\ delta _ {p} =0,43 \) и \ (F =29,8 \) T. Это согласуется с теоретическим предсказанием и наблюдаемый dHvA происходит из состояния топологической поверхности. Следуя соотношению Онзагера [44], \ (F =\ frac {\ hbar K_F ^ {2}} {2 \ pi} \), можно оценить, что \ (K_ {F} =0,030 \) Å ^{- 1} согласуется с сообщенным значением ARPES. Эти результаты предполагают, что колебания dHvA происходят из топологического состояния поверхности.

Заключение

В данной работе мы исследовали магнитное поведение монокристалла топологического изолятора Sb \ (_ {2} \) Te \ (_ {3} \), легированного никелем. Ниже температуры Нееля наблюдалась петля гистерезиса с низким коэрцитивным полем. Магнитная восприимчивость обнаруживает скачок температуры Нееля, не зависящий от внешнего магнитного поля. Магнитная восприимчивость процессов охлаждения в нулевом поле и охлаждения в поле совпадают выше температуры Нееля и являются бифуркационными ниже температуры Нееля. Расщепление магнитной восприимчивости больше при меньшем внешнем магнитном поле. Расщепление магнитной восприимчивости больше не наблюдается, когда энергия анизотропии магнитного момента ниже энергии магнитного момента при 0,7 Тл. Наше исследование подтверждает, что эти характеристики магнитной восприимчивости происходят из антиферромагнитного порядка, сопровождаемого слабым ферромагнетизмом. Извлеченная насыщенная магнитная восприимчивость хорошо согласуется с тенденцией измеренного каспа магнитной восприимчивости. Это указывает на то, что широко наблюдаемый куспид восприимчивости может быть результатом слабого ферромагнетизма. Колебания dHvA согласуются с теоретическим предсказанием. Это подтверждает, что наблюдаемая осцилляция dHvA связана с топологическим состоянием поверхности.

Доступность данных и материалов

Наборы данных, созданные во время и / или проанализированные в ходе текущего исследования, доступны у соответствующих авторов по разумному запросу.

Сокращения

XPD:

Рентгеновская дифракция

EDS:

Энергодисперсионная рентгеновская спектроскопия

ARPES:

Фотоэмиссионная спектроскопия с угловым разрешением

dHvA:

Де Хаас-Ван Альфен