Наблюдение зависимых от уровня Ландау колебаний Ааронова-Бома в топологическом изоляторе

Введение

Интерференция Ааронова-Бома (AB) возникает из-за интерференции волновой функции носителя в петле, которая может быть узорчатым кольцом [1, 2], геометрической структурой материала [3–6, 8–11] или траекторией переноса носителя [12]. Магнитное поле, Б , через петлю вызовет фазовый сдвиг волновой функции несущей, что приведет к периодическим интерференционным колебаниям волновой функции. Этот период колебаний зависит от транспортных характеристик носителей, таких как длина когерентности и подвижность носителей [3, 12]. Квантовая интерференция - отличный инструмент для определения характеристик переноса материала и понимания внутренних механизмов. Из-за короткой длины когерентности носителей и небольшого кванта потока квантовая интерференция в основном наблюдается в нанопроволоках с высокой подвижностью или структурированных нанокольцах при низких B [3–6, 8–11]. Отчеты о макроскопической системе при высоком B редки. Работы по квантовой интерференции AB при высоких B менее изучены, а соответствующий механизм менее понятен.

В данной работе квантовые колебания выполнялись в BiSbTe ₃ макрочастица топологического изолятора при высоких B . Помимо осцилляции Шубникова-де Гааза (ШдГ), наблюдались осцилляции типа Ааронова-Бома (ABL). Период колебаний АПС составляет B -зависимы и отличаются от традиционных колебаний AB, период колебаний которых не зависит от B . Наблюдаемый период колебаний ABL постоянен на каждом уровне Ландау (LL), который определяется по колебаниям ШдГ. Более короткие периоды колебаний наблюдаются при меньших ЛП. Период колебаний пропорционален квадратному корню из LL при температурах. Отношение периода колебаний АПС к эффективной массе имеет слабую зависимость ЛЛ. Зависимые от LL колебания ABL могут возникать из-за зависимой от LL эффективной массы.

Экспериментальный метод

Условия роста BiSbTe ₃ монокристалл такой же, как и наша предыдущая работа по топологическим изоляторам [13–16]. Наша предыдущая работа продемонстрировала, что ТИ с чрезвычайно высокой однородностью можно получить с помощью метода RHFZ [13–16]. Рамановский, EDS и XPS спектр доказали, что кристалл представляет собой BiSbTe ₃ . БиСбТе ₃ Монокристаллические чешуйки получали методом скотча. Геометрия сколотых чешуек составляет примерно 3 мм в длину, 2 мм в ширину и 170 μ м толщиной. Измерения магнитотранспорта были выполнены с использованием стандартной шестизоновой техники в коммерческом аппарате (Quantum Design PPMS) с B до 14 т. B наносился перпендикулярно большой поверхности скола. Точки данных берутся на 100 Гаусс в диапазоне магнитного поля от 6 до 14 Тл в режиме постоянного магнитного поля, а не в режиме качающегося магнитного поля.

Результаты и обсуждение

На рисунке 1 показано магнитосопротивление (MR) как функция B . . R (14T) / R (0T) достигает 10 и превышает большинство заявленных значений в Bi _x Сб _{2− x} Te _y Se _{3− y} топологические изоляторы [17–23, 23–33]. Как теоретические, так и экспериментальные исследования подтверждают, что отношение MR пропорционально подвижности носителей [34]. Измеренное высокое отношение MR подтверждает высокое качество нашего BiSbTe ₃ образец. Верхняя левая вставка показывает d R / d Б как функция 1 / B . Он показывает, что периодические колебания, а также пики и спады колебаний находятся на одном и том же B при 2 и 8 К. Это известно как колебание ШдГ, возникающее в двумерной системе. Период колебаний ШдГ соответствует вектору импульса Ферми k _f . В правом нижнем углу вставки показано быстрое преобразование Фурье (БПФ) колебаний ШдГ. Резкий пик при 48 Тл наблюдается как для 2, так и для 8 К. Следуя соотношению Онзагера, можно оценить k _f через \ (F =\ frac {\ hbar k_ {f} ^ {2}} {2e} \), где F - частота колебаний ШдГ. F =48 Тл приводит к k _f =3,8Å ^-1 , что согласуется с наблюдаемым значением ARPES из другой партии того же кристалла и значениями, опубликованными в литературе [35]. Это поддерживает высокое качество и единообразие нашего BiSbTe ₃ кристалл. На левой верхней вставке наряду с осцилляцией ШдГ видны осцилляции с коротким периодом. Чтобы подавить влияние колебаний ШдГ и извлечь колебательные характеристики, d ² R / d Б ² выполняется.

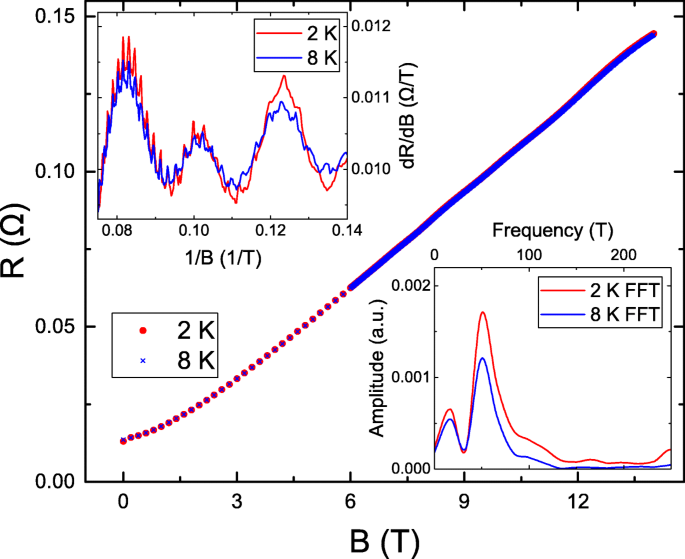
Магнитосопротивление как функция магнитных полей при 2 и 8 К. На вставке вверху слева показано d R / d Б как функция обратных магнитных полей. В нем обнаруживаются периодические колебания. В правом нижнем углу вставки показано быстрое преобразование Фурье колебаний ШдГ и острый пик при 48 Тл как для 2, так и для 8 К

На рисунке 2 изображен d R / d Б и d ² R / d Б ² как функция от B при 2 и 8 К. Пунктирными линиями отмечены пики колебаний в d ² R / d Б ² , а длинные пунктирные линии соответствуют B LL, которые определяются по извлеченной частоте колебаний ШдГ. Периодические колебания аналогичны колебаниям АБ. Период колебаний AB выражается как \ (\ Delta B =\ frac {\ Phi} {A} \). Φ - квант потока, где \ (\ frac {h} {e} \), а A это геометрическая область, замкнутая траекториями носителей тактового и противочасового счета в замкнутой структуре. Из-за небольшого кванта потока колебания AB в основном наблюдаются в ограничении искусственными наноструктурами [1, 2], такими как нанокольца и нанопроволоки [3–11]. Недавно сообщалось, что траектория упругого рассеяния носителей может образовывать серию связанных замкнутых контуров в макроскопической системе. А Б Поток через эти петли вызовет фазовый сдвиг волновой функции несущей и приведет к периодическим колебаниям ABL [12]. Извлеченная длина упругого рассеяния составляет примерно 150 нм, что соответствует периоду колебаний 0,02 Тл и согласуется с нашими экспериментальными наблюдениями.

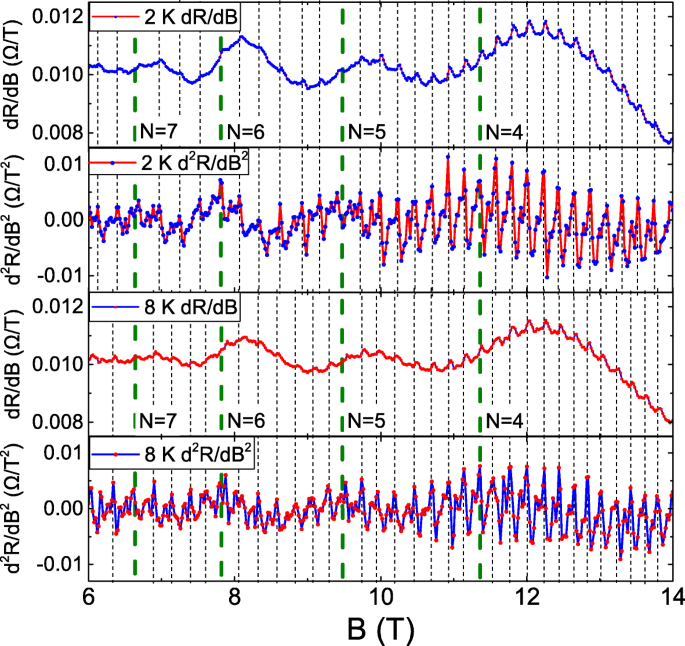
d R / d Б и d ² R / d Б ² как функция от B при 2 и 8 К. Он показывает периодические колебания, а период колебаний является зависимостью от уровня Ландау

Следуя пунктирным линиям на рис. 2, можно заметить, что период колебаний постоянен на каждом LL, а период колебаний короче на более низких LL. Это поведение отличается от традиционного колебания AB. Чтобы извлечь и определить эти периоды колебаний, выполняется БПФ на разных LL. На рис. 3 показано БПФ при различных значениях нижнего предела при 2 и 8 К, и на нем четко видна более высокая частота колебаний при более низких значениях нижнего предела при 2 и 8 К.

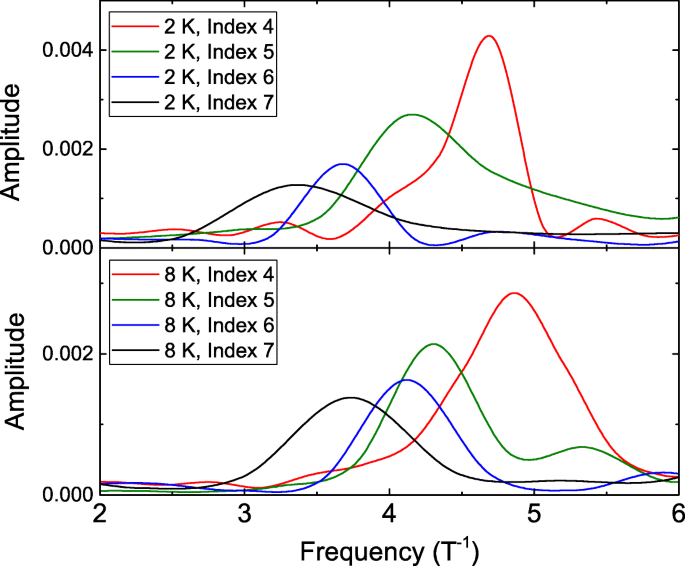
Быстрое преобразование Фурье d R / d Б при разных уровнях и температурах Ландау. Более высокий пик частоты колебаний наблюдается на более низких уровнях Ландау

Аналогичная ЛЛ-зависимая осцилляция АПС наблюдается в целочисленном квантовом режиме Холла в полупроводниковом двумерном электронном газе [36, 37]. Это было интерпретировано либо как конструктивная интерференция одномерного электрона, движущегося по краевым каналам, либо как квантовая интерференция волн краевых электронов. Путь транспортировки носителей в разных краевых каналах приводит к разным эффективным областям в ограниченном шаблоне и, в конечном итоге, к разным периодам колебаний ABL в краевых каналах на разных LL [38-40]. Дальнейшие исследования электрических интерферометров Фабри-Перо в целочисленном и дробном квантовом режиме Холла показывают, что период колебаний ABL связан с периодом потока соотношением \ (\ frac {\ Phi} {f} \), где f - полностью занятый LL в перетяжках. Ожидается, что период колебаний будет \ (\ frac {\ Phi} {A f} \), где A - геометрическая область ограниченной формы [41, 42].

В таблице 1 перечислены периоды колебаний, извлеченные из БПФ при различных LL и температурах. Анализ показывает, что отношение периода колебаний к квадратному корню из LL постоянно при каждой температуре. Это отличается от поведения интерферометра Фабри-Перо, в котором колебания обратно пропорциональны LL [41, 42]. С другой стороны, электрическая интерференция Фабри-Перо возникает из-за связи траекторий носителей между различными LL изнутри и снаружи ограниченного паттерна [37]. Колебания сильно связаны с геометрией рисунка. На поверхности наших образцов нет искусственных узоров, и не должно быть подходящих каналов связи между разными ЛЖ. Кроме того, геометрические размеры наших образцов находятся в миллиметровом масштабе, и соответствующий период колебаний AB был бы слишком мал, чтобы его можно было обнаружить. Несмотря на эти отличия от существующих работ, мы думаем, что помимо геометрической площади и длины когерентности носителей, характеристики собственных носителей могут играть решающую роль в LL-зависимых колебаниях ABL [3, 43].

Следуя теории Лифшица-Косевича (ЛК), можно выделить характерные параметры транспортных носителей в поверхностном состоянии топологического изолятора, а температурная зависимость амплитуды колебаний ШдГ выражается как

где \ (\ lambda (T / B) =(2 \ pi ^ {2} k_ {B} Tm_ {cyc}) / (\ hbar eB) \). На рис. 4 показана извлеченная нормализованная амплитуда колебаний ШдГ в зависимости от температуры при различных ЛП. Это хорошо согласуется с теорией LK и выявляет разные тенденции на разных LL. Результаты подгонки подтверждают, что м _цикл =0,152 м ₀ , 0,170 м ₀ , 0,185 м ₀ , и 0,191 м ₀ , где м ₀ - масса свободного электрона, для N =4, 5, 6 и 7 соответственно. Эти значения согласуются с данными об эффективных массах топологических изоляторов [21, 22]. Эта эффективная масса, зависящая от уровня Ландау, недавно наблюдалась в трехмерном полуметалле Дирака ZrTe ₅ [44]. Однако происхождение эффективной массы, зависящей от магнитного поля, пока не ясно. Это требует дальнейшего изучения, чтобы прояснить внутренний механизм. Различная эффективная масса будет напрямую отклонять характеристику собственного переноса носителей заряда на поверхности Ферми, такую ​​как скорость Ферми, которая напрямую связана с длиной фазовой когерентности носителей. Более высокая эффективная масса приведет к меньшей длине когерентности, что соответствует более длительному периоду колебаний типа AB. Это качественно согласуется с нашим экспериментальным наблюдением. Как показано в таблице 1, отношение периода AB-подобных колебаний к эффективной массе показывает слабую зависимость LL. Эффективная масса, зависящая от уровня Ландау, может быть одним из внутренних эффектов, которые приводят к периоду колебаний, зависящему от LL.

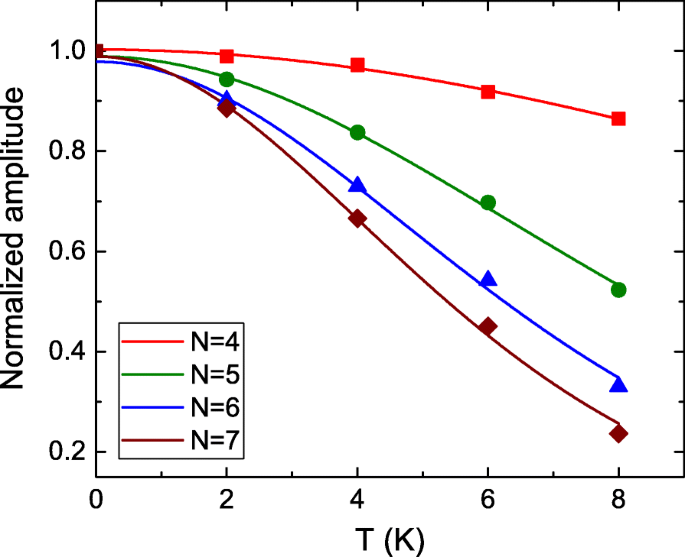
Извлеченная нормализованная амплитуда колебаний ШдГ как функция температуры на разных уровнях Ландау. Это хорошо согласуется с теорией ЛК и выявляет разные тенденции на разных уровнях Ландау

LL - транспортная характеристика двумерной системы. Это указывает на то, что LL-зависимые колебания могли происходить от носителя поверхностного состояния в ТИ. Ягодная фаза характерна для транспортных носителей. Выделение фазы Берри может помочь идентифицировать источник этих LL-зависимых периодических колебаний AB. Определим номер индекса колебания AB, разделив соответствующий B пиков колебаний в d Б / d Б на соответствующий период колебаний в LL. Он показывает, что порядковый номер пика колебаний в d Б / d Б соответствует N +0.25, где N является целым числом для всех колебаний при различных ЛП и температурах. Это также подтверждает, что период колебаний AB связан с LL. На рисунке 5 показано, что числа индекса колебаний AB пропорциональны B . при разных ЛП и температурах. Пересечение составляет 0,25, что указывает на сдвиг фазы 0,5 на графике колебаний AB. Это поддерживает фазу Берри: π и наблюдаемые колебания AB могут быть характеристикой переноса носителей для поверхностного состояния в нашем BiSbTe ₃ топологический изолятор [45].

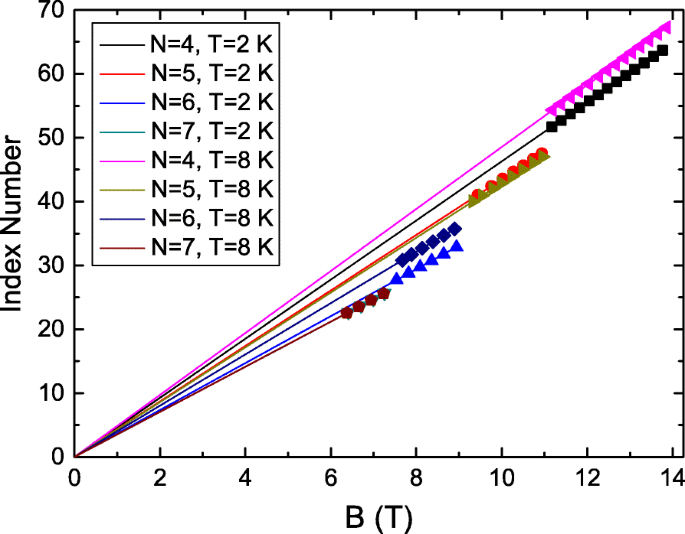
Номер индекса колебания AB как функция от B при разных уровнях и температурах Ландау. Пересечение составляет 0,25, что указывает на сдвиг фазы 0,5 на графике колебаний AB. Это поддерживает фазу Берри: π

Заключение

Мы сообщили о квантовых колебаниях в BiSbTe ₃ топологический изолятор макрочастица. Помимо осцилляции Шубникова-де Гааза (ШдГ), он обнаруживает колебания типа Ааронова-Бома (АПС). Период колебаний АПС составляет B -зависимый. Период колебаний АПС постоянен на каждом уровне Ландау (LL). Более короткие периоды колебаний наблюдались при меньших нижних пределов, что определялось по колебаниям ШдГ. Период колебаний пропорционален квадратному корню из LL при различных температурах. Отношение периода колебаний АПС к эффективной массе имеет слабую зависимость ЛЛ. Зависимые от LL колебания ABL могут возникать из-за зависимой от LL эффективной массы.

Доступность данных и материалов

Наборы данных, созданные во время и / или проанализированные в ходе текущего исследования, доступны у соответствующих авторов по разумному запросу.

Сокращения

EDS:

Энергодисперсионная рентгеновская спектроскопия

XPS:

Рентгеновская фотоэлектронная спектроскопия

ARPES:

Фотоэмиссионная спектроскопия с угловым разрешением

SdH:

Шубников-де Хаас