Зависимость электронных и оптических свойств многослоев MoS2 от межслоевой связи и сингулярности Ван Хова
Аннотация
В этой статье структурные, электронные и оптические свойства MoS 2 мультислои исследуются методом первых принципов. До шести слоев MoS 2 были сравнительно изучены. Ковалентность и ионность в MoS 2 Показано, что монослой сильнее, чем в объеме. Когда количество слоев увеличивается до двух или более двух, расщепление полосы становится значительным из-за межслойной связи. Мы обнаружили, что длинные плато возникают в мнимых частях диэлектрической проницаемости \ ({\ varepsilon} _2 ^ {xx} \ left (\ omega \ right) \) и совместной плотности состояний (JDOS) MoS 2 многослойные, обусловленные особенностями Ван Хова в двумерном материале. Одна, две и три маленьких ступеньки появляются на порогах длинного плато \ ({\ varepsilon} _2 ^ {xx} \ left (\ omega \ right) \) и JDOS для монослоя, двухслойного и трехслойного соответственно. . По мере дальнейшего увеличения количества слоев количество маленьких ступенек увеличивается, и ширина маленьких ступенек соответственно уменьшается. Из-за межслойной связи самое длинное и самое короткое плато JDOS происходит от монослоя и объема, соответственно.
Введение
Дисульфид молибдена (MoS 2 ) является одним из типичных дихалькогенидов переходных металлов и широко используется в качестве катализатора [1] и материала для хранения водорода [2, 3]. Из-за сильных взаимодействий в плоскости и слабых ван-дер-ваальсовых взаимодействий между MoS 2 атомные слои [4, 5], MoS 2 кристаллы были известны как важная твердая смазка на протяжении многих лет [6, 7]. Монослой MoS 2 , так называемый 1 H -MoS 2 , был отслоен от объемного MoS 2 с помощью микромеханического скола [8]. Так называемые 2 H -MoS 2 (среди 1T , 2H , 3R ) является наиболее устойчивой структурой объемного MoS 2 [9, 10] и представляет собой полупроводник с непрямой запрещенной зоной 1,29 эВ [4, 11, 12]. Монослой MoS 2 также привлек большое внимание из-за своей двумерной природы и графеноподобной сотовой структуры. Интересно, что однослойный MoS 2 имеет прямую запрещенную зону 1,90 эВ [4, 13], которая может использоваться как токопроводящий канал полевых транзисторов [14]. С другой стороны, нулевая запрещенная зона графена ограничивает его применение в оптике и применении транзисторов [15,16,17,18]. Более того, теоретические и экспериментальные работы показывают, что ширина запрещенной зоны электронов уменьшается с увеличением количества MoS 2 слои увеличены [19,20,21,22]. Межслойное сцепление многослойного MoS 2 чувствительна к толщине слоя [21]. Некоторые исследования многослойного MoS 2 доступны [19,20,21,22,23,24,25]; однако электронные структуры и оптические свойства многослойного MoS 2 до сих пор не установлены, особенно в отношении зависящих от слоя физических свойств, связанных с межслойной связью. Особенность Ван Хова (VHS) играет важную роль в оптических свойствах [26, 27]. Единственными доступными критическими точками в двумерных материалах являются точки P 0 ( P 2 ) и P 1 типа, которые проявляются в виде ступеньки и логарифмической особенности [26, 27]. В этой статье мы анализируем электронные и оптические свойства MoS 2 . связанных с сингулярностью Ван Хова, слой за слоем и до шести атомных слоев.
В настоящее время расчеты из первых принципов успешно выполняются для изучения структурных, электронных и оптических свойств самых разных материалов. В этой работе мы систематически исследовали электронные и оптические свойства монослойного, многослойного и объемного MoS 2 с помощью расчетов ab initio. Особое внимание уделяется обсуждению оптических свойств. Наши результаты показывают, что для E || x мнимые части диэлектрической функции \ ({\ varepsilon} _2 ^ {xx} \ left (\ omega \ right) \) имеют длинные плато. На этих порогах этих плато \ ({\ varepsilon} _2 ^ {xx} \ left (\ omega \ right) \) монослоя, бислоя и трехслоя демонстрируют один, два и три маленьких шага, соответственно. Мнимая часть диэлектрической функции также анализируется совместной плотностью состояний и элементами матрицы перехода. Подробно обсуждается JDOS в сочетании с ленточными структурами и особенностями Ван Хова.
Методы
Настоящие расчеты были выполнены с использованием пакета Венского ab initio моделирования (VASP) [28, 29], который основан на теории функционала плотности, базисе плоских волн и представлении расширенной волны проектора (PAW) [30]. Обменно-корреляционный потенциал рассматривается в рамках приближения обобщенного градиента (GGA) в форме функционала Пердью-Берк-Эрнцерхоф (PBE) [31]. Чтобы учесть слабое межслоевое притяжение в этом слоистом кристалле, были выполнены расчеты PBE-D2 [32], которые включают полуэмпирическую поправку Ван-дер-Ваальса. Для получения более точных значений ширины запрещенной зоны в этой работе также выполняются расчеты гибридного функционала Хейда-Скузерии-Эрнцерхофа (HSE06) [33,34,35,36]. Волновые функции всех рассчитанных систем разложены по плоским волнам с обрезанием по кинетической энергии 500 эВ. Интеграция зоны Бриллюэна (ЗБ) рассчитывается с использованием специального k -точечной выборки схемы Монкхорста-Пака [37], с размером 45 × 45 × 1 Γ -центрированная сетка для однослойного и многослойного MoS 2 и сетка 45 × 45 × 11 для объемного MoS 2 для расчетов PBE-D2. Для расчетов HSE06 9 × 9 × 1 Γ -центрированная сетка используется для однослойного и многослойного MoS 2 . Для однослойного и многослойного MoS 2 , все вычисления моделируются суперячейкой с вакуумным пространством 35 Å в Z -направление, чтобы избежать взаимодействия между соседними MoS 2 плиты. Все атомные конфигурации полностью релаксированы до тех пор, пока силы Геллмана-Фейнмана на всех атомах не станут меньше 0,01 эВ / Å. Наши спин-поляризованные расчеты показывают, что зонные структуры MoS 2 мультислои довольно нечувствительны к спин-поляризованному эффекту (см. Дополнительный файл 1:Рисунок S1); поэтому все представленные результаты расчетов основаны на схеме без спиновой поляризации.
Экситонные эффекты в монослое MoS 2 оказались значительными и наблюдались с помощью фотолюминесценции. Мы использовали квазичастицу G 0 W 0 метод [38] и уравнение Бете-Солпитера (BSE) [39, 40] для учета экситонных эффектов. Ширина запрещенной зоны монослоя MoS 2 рассчитаны равными 2,32 и 2,27 эВ для k -точечные сетки 15 × 15 × 1 и 24 × 24 × 1 Γ -центрированная сетка, полученная G 0 W 0 с расчетами SOC. Мнимые части диэлектрической проницаемости показаны на рис. 1, рассчитанные как из G 0 W 0 и G 0 W 0 + Методы BSE. Обнаружены два экситонных пика при 1.84 и 1.99 эВ, что хорошо согласуется с экспериментальными наблюдениями [4, 41]. Хотя G 0 W 0 + Схема BSE могла бы лучше описать экситонные эффекты, в этой статье мы представляем только результаты (без экситонных пиков) под функционалом GGA-PBE.
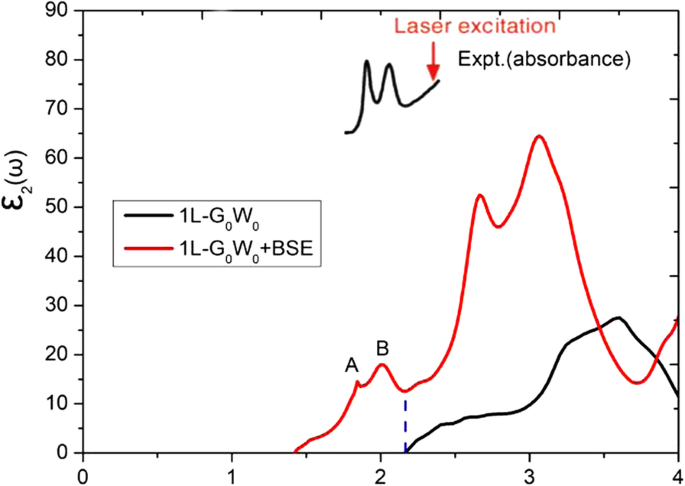
Мнимые части диэлектрической проницаемости для монослоя MoS 2 , используя G 0 W 0 и G 0 W 0 + Методы BSE соответственно. Экспериментальный спектр поглощения MoS 2 взят из работы. [4]
Результаты и обсуждение
Электронные структуры MoS 2 Многослойные
Кристаллический MoS 2 встречается в природе и имеет три кристаллических типа:1 T , 2 H , и 3 R , что соответствует кристаллам с тригональной, гексагональной и ромбоэдрической примитивными ячейками соответственно [9]. 2 H -MoS 2 известна как наиболее устойчивая структура [10]; поэтому мы рассматриваем только 2 H тип массового MoS 2 в этой работе. Группа 2 H -MoS 2 имеет гексагонально-слоистую структуру, состоящую из слоев атомов молибдена, окруженных шестью атомами серы, с наложенными друг на друга листами S-Mo-S (как показано на рис. 2). Соседние листы навалом 2 H -MoS 2 слабо связаны со слабыми ван-дер-ваальсовыми взаимодействиями. Однослойный MoS 2 затем легко отслаивается от основной массы. Постоянные решетки объемного MoS 2 рассчитываются как a =b =3,19Å, c =12,41 Å, что соответствует заявленным значениям a =b =3,18 Å, c =13,83 Å [18]. Оптимизированные постоянные решетки для однослойного MoS 2 являются a =b =3,19 Å, что соответствует объемному MoS 2 . Как показано в Таблице 1, вычисленные постоянные решетки в a , b направления одинаковы для разного количества слоев MoS 2 . Об этом также сообщили Kumar et al. [19], что постоянные решетки ( a, b ) монослоя MoS 2 практически идентичны основной части.
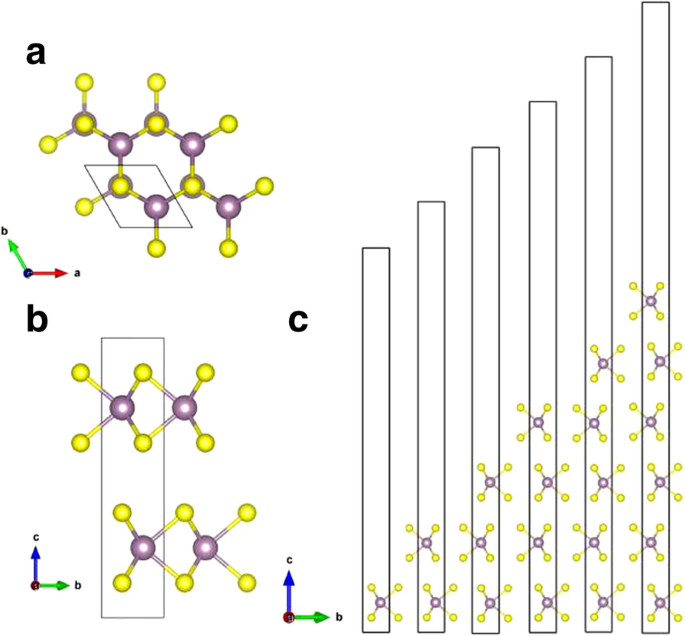
а Вид сверху и b вид сбоку на bulk-MoS 2 . c Вид сбоку на однослойные, двухслойные, трехслойные, а также четырех-, пяти- и шестислойные структуры MoS 2 . Элементарная ячейка показана на b . . Фиолетовые и желтые шары представляют собой атомы Mo и S соответственно
На рисунке 3 показаны рассчитанные зонные структуры и плотность электронных состояний (DOS) различного количества слоев MoS 2 . . Результаты для однослойного, двухслойного, трехслойного и четырехслойного, а также для объемного MoS 2 приведены на рис. 3, а результаты для пяти- и шестислойного MoS 2 очень похожи на четырехслойные и наливные. Для однослойного MoS 2 , как максимум валентной зоны (VBM), так и минимум зоны проводимости (CBM) появляются в K-точке BZ, показывая прямую ширину запрещенной зоны 1,64 эВ. Для двухслойного и трехслойного MoS 2 , оба VBM расположены в точке Γ, в то время как оба CBM находятся в точке K, вызывая непрямые промежутки 1,17 и 1,08 эВ, соответственно. Однако, поскольку количество MoS 2 слоев увеличивается до четырех и выше четырех, все многослойные MoS 2 показывают те же символы, что VBM находится в точке Γ, в то время как CBM находится между точками Γ и K, что такое же, как в балке. Непрямая запрещенная зона составляет 1,03 эВ, 1,01 эВ, 0,99 эВ, 0,93 эВ для четырех-, пяти-, шестислойного MoS 2 . , и навалом соответственно. Расчеты PBE-D2 и HSE06 (таблица 1) показывают, что основная ширина запрещенной зоны монотонно увеличивается, когда количество MoS 2 слоев уменьшается, что связано с большим удержанием электронов в слое [4, 5, 19, 42]. Более того, когда объемный MoS 2 пластина уменьшается до однослойной, она превращается в прямозонный полупроводник, как упоминалось ранее, объемный MoS 2 является непрямозонным полупроводником. На рис. 3а показан график зонной структуры объемного MoS 2 показать расщепление полос (по сравнению с однослойным MoS 2 ), в основном вокруг  - точка, обусловленная межслойным сцеплением [16]. Ленточные конструкции для двухслойного (2L) и более 2L MoS 2 демонстрируют аналогичное расщепление полос из-за межслоевого взаимодействия. Однако расщепление полос в объеме несколько более значимо, чем в многослойном MoS 2 , что указывает на (немного) более сильную межслойную связь в объеме, чем в мультислоях. С другой стороны, расщепление полос в окрестности точки K в BZ очень мало. Электронные состояния в точке K для самой высокой занятой зоны в основном состоят из d xy и \ ({d} _ {x ^ 2- {y} ^ 2} \) орбитали атомов Mo, а также небольшие части ( p x , p y ) -орбитали атомов S (показаны на рис. 4б). Атомы Mo расположены в среднем слое листа S-Mo-S, что вызывает пренебрежимо малую межслойную связь в точке K (поскольку ближайшие атомы между MoS 2 слои S и S). Как показано на рис. 4, более сильная межслойная связь в точке Γ может быть обнаружена по сравнению с таковой в точке K, поскольку в электронных состояниях в точке Γ для самой высокой занятой зоны преобладают \ ({d} _ {z ^ 2} \ ) орбитали атомов Мо и p z орбитали атомов S. Следовательно, S-S-связь (межслойная связь) явно сильнее в точке Γ, чем в точке K. Наши результаты согласуются с другими теоретическими работами [21]. Вообще говоря, электронная плотность состояний многослойного MoS 2 аналогичны массовым MoS 2 (см. рис. 3), поскольку объемный MoS 2 на самом деле многослойный материал со слабым взаимодействием между MoS 2 слои.
- точка, обусловленная межслойным сцеплением [16]. Ленточные конструкции для двухслойного (2L) и более 2L MoS 2 демонстрируют аналогичное расщепление полос из-за межслоевого взаимодействия. Однако расщепление полос в объеме несколько более значимо, чем в многослойном MoS 2 , что указывает на (немного) более сильную межслойную связь в объеме, чем в мультислоях. С другой стороны, расщепление полос в окрестности точки K в BZ очень мало. Электронные состояния в точке K для самой высокой занятой зоны в основном состоят из d xy и \ ({d} _ {x ^ 2- {y} ^ 2} \) орбитали атомов Mo, а также небольшие части ( p x , p y ) -орбитали атомов S (показаны на рис. 4б). Атомы Mo расположены в среднем слое листа S-Mo-S, что вызывает пренебрежимо малую межслойную связь в точке K (поскольку ближайшие атомы между MoS 2 слои S и S). Как показано на рис. 4, более сильная межслойная связь в точке Γ может быть обнаружена по сравнению с таковой в точке K, поскольку в электронных состояниях в точке Γ для самой высокой занятой зоны преобладают \ ({d} _ {z ^ 2} \ ) орбитали атомов Мо и p z орбитали атомов S. Следовательно, S-S-связь (межслойная связь) явно сильнее в точке Γ, чем в точке K. Наши результаты согласуются с другими теоретическими работами [21]. Вообще говоря, электронная плотность состояний многослойного MoS 2 аналогичны массовым MoS 2 (см. рис. 3), поскольку объемный MoS 2 на самом деле многослойный материал со слабым взаимодействием между MoS 2 слои.
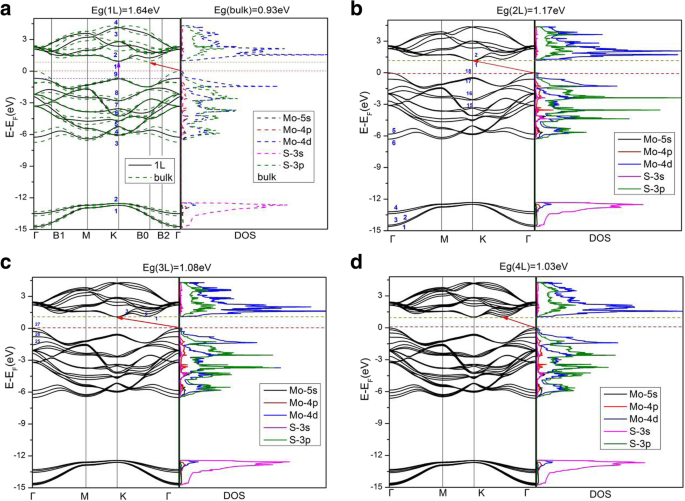
Расчетные зонные структуры и плотность состояний a однослойный (сплошные линии) и объемный (пунктирные линии), b двухслойный, c трехслойный и d четырехслойный MoS 2 . В а , самые высокие занятые зоны для объема и монослоя в точке K устанавливаются на одну и ту же энергию. Минимальная зона проводимости массы находится в точке B0
Распределение зарядов в самой высокой занимаемой полосе в a точка  и b точка K для объемного MoS 2 . Значение изоповерхности установлено равным 0,004 э / Å
3
.
и b точка K для объемного MoS 2 . Значение изоповерхности установлено равным 0,004 э / Å
3
.
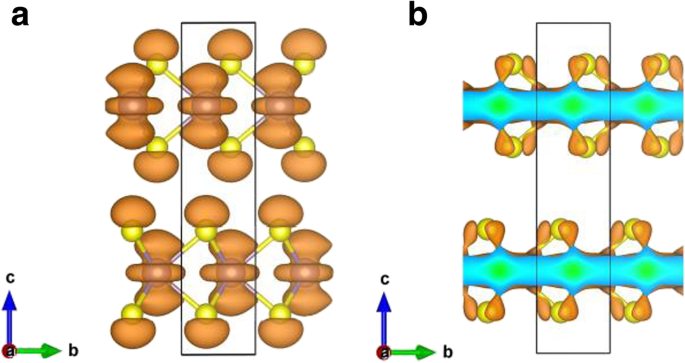
Чтобы глубоко изучить природу связывания в однослойном MoS 2 плотность деформационного заряда представлена на рис. 5а. Плотность деформационного заряда определяется как Δρ 1 ( г ) = ρ ( г ) - ∑ μ ρ атом ( г - R μ ) где ρ ( г ) - полная плотность заряда, а ∑ μ ρ атом ( г - R u ) обозначает суперпозицию независимых плотностей атомных зарядов. Результаты демонстрируют, что связывание в MoS 2 монослой характеризуется четкой ковалентностью (сплошные контурные линии между атомами Mo-S), а также сильными ионными взаимодействиями (представлены чередующимися участками пунктирных и сплошных контуров). Чтобы увидеть силу сцепления в монослое MoS 2 по сравнению с объемным, разница в плотности заряда между монослоем и объемным MoS 2 , Δρ 2 ( г ), также представлена на рис. 5б. Разница плотности заряда определяется как Δρ 2 ( г ) = ρ 1 L ( г ) - ρ навалом ( г ), где ρ 1 L ( г ) и ρ навалом ( г ) - полные плотности заряда монослоя и объемного MoS 2 , соответственно. Рисунок 5b указывает на более сильную электронную связь в случае монослоя, чем в объеме, что отражается в большем накоплении заряда (сплошные контурные линии) между атомами Mo-S в монослое, а также в более сильной ионной связи в слое. однослойный MoS 2 поскольку чередующиеся области штриховых и сплошных контуров на рис. 5б более значительны, чем в объеме. Более того, график разности зарядов (рис. 5b) показывает, что атом Mo монослоя потерял больше электронов, чем атом Mo в объеме; следовательно, ионность монослоя сильнее, чем объемного. Однако следует отметить, что порядок величины разности зарядов на рис. 5б довольно мал (интервал изолиний на рис. 5б составляет всего 2,5 × 10 −4 э / Å 3 ). Судя по эффекту квантового ограничения, опять же, внутрислойное взаимодействие монослоя должно быть сильнее объемного. Следовательно, ожидается, что ширина запрещенной зоны монослоя (1,64 эВ) будет больше, чем в объеме (0,93 эВ). Квантовое ограничение уменьшается с увеличением номера слоя [4, 42], что усиливает межслойное взаимодействие и уменьшает внутрислойное взаимодействие. Таким образом, ширина запрещенной зоны MoS 2 уменьшается с увеличением межслойной связи. Перераспределение межслойной плотности заряда для двухслойного MoS 2 , Δρ 3 ( г ), также представлены на рис. 5в. Значок Δρ 3 ( г ) определяется выражением Δρ 3 ( г ) = ρ 2 L ( г ) - ρ слой1 ( г ) - ρ слой2 ( г ), где ρ 2 L ( г ), ρ слой1 ( г ), ρ слой2 ( г ) - плотности заряда двухслойного MoS 2 , первый слой двухслойного MoS 2 и второй слой двухслойного MoS 2 , соответственно. Плотности заряда слоя 1 и 2 двухслойного MoS 2 рассчитываются с использованием соответствующей структуры в двухслойном MoS 2 . Перенос заряда из MoS 2 слои (бислой) к промежуточной области между MoS 2 Слои хорошо видны на рис. 5в и показаны сплошными контурными линиями. Ионные взаимодействия между атомными слоями в двухслойном MoS 2 также четкие, что видно по чередованию участков пунктирных и сплошных контуров. Опять же, порядок величины межслоевых плотностей зарядов, Δρ 3 ( г ), очень малы (интервал изолиний всего 2,5 × 10 -4 э / Å 3 ). Как правило, перераспределение плотности заряда между слоями в 2L, 3L,…, объемном MoS 2 все системы очень похожи.
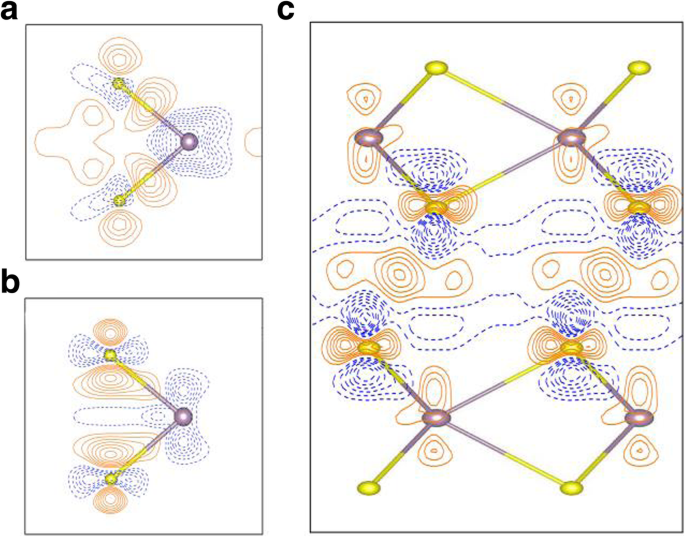
а Плотность деформационного заряда, Δ ρ 1 ( г ) = ρ ( г ) - ∑ μ ρ атом ( г - R μ ), в монослое MoS 2 . б Различия между плотностями заряда монослоя и соответствующего слоя объема. c Перераспределение межслоевой плотности заряда двухслойного MoS 2 . Интервал изолиний а равно 2,5 × 10 −2 э / Å 3 , а оба варианта b и c равны 2,5 × 10 −4 э / Å 3 . Сплошные оранжевые и пунктирные синие линии соответствуют Δ ρ > 0 и Δ ρ <0 , соответственно
Оптические свойства MoS 2 Многослойные
После получения основных электронных структур материала можно исследовать его оптические свойства. Мнимая часть диэлектрической проницаемости \ ({\ varepsilon} _2 ^ {\ alpha \ beta} \ left (\ omega \ right) \) определяется следующим уравнением [43]:
$$ {\ displaystyle \ begin {array} {c} {\ varepsilon} _2 ^ {\ alpha \ beta} \ left (\ omega \ right) =\ frac {4 {\ pi} ^ 2 {e} ^ 2} {\ Omega} {\ lim} _ {q \ to 0} \ frac {1} {q ^ 2} \ underset {c, v, k} {\ Sigma} 2 {w} _k \ delta \ left ({E } _ {ck} - {E} _ {vk} - \ mathrm {\ hslash} \ omega \ right) \\ {} \ times \ left \ langle {u} _ {ck + {e} _ {\ alpha} q } | {u} _ {vk} \ right \ rangle \ left \ langle {u} _ {ck + {e} _ {\ beta} q} | {u} _ {vk} \ right \ rangle \ ast \ end { массив}} $$ (1)где индексы α и β обозначают декартовы направления, c и v относятся к зоне проводимости и валентной зоне, E ck и E вк - энергии зоны проводимости и валентной зоны соответственно. Инверсия Крамерса-Кронига может применяться для получения действительной части диэлектрической функции \ ({\ varepsilon} _1 ^ {\ alpha \ beta} \ left (\ omega \ right) \), определяемой мнимой частью \ ({\ varepsilon} _2 ^ {\ alpha \ beta} \ left (\ omega \ right) \):
$$ {\ varepsilon} _1 ^ {\ alpha \ beta} \ left (\ omega \ right) =1 + \ frac {2} {\ pi} P {\ int} _0 ^ {\ infty} \ frac {\ varepsilon_2 ^ {\ alpha \ beta} \ left (\ omega \ hbox {'} \ right) \ omega \ hbox {'}} {\ omega {\ hbox {'}} ^ 2 - {\ omega} ^ 2 + i \ эта} d \ omega \ hbox {'} $$ (2)в котором P представляет собой главное значение. Начиная с MoS 2 имеет одноосную структуру, ε xx ( ω ) тогда идентично ε гг ( ω ). В этой работе нам достаточно обсудить электрический вектор E . который параллелен x-y плоскости, т. е. E || x параллельно MoS 2 х-у самолет.
Для исследования детальных оптических спектров MoS 2 системе коэффициент поглощения α ( ω ) и коэффициент отражения R ( ω ) вычислялись по действительной части ε 1 ( ω ) и мнимая часть 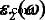 диэлектрической функции. Уравнения упомянутых параметров представлены ниже:
диэлектрической функции. Уравнения упомянутых параметров представлены ниже:
Если матричный элемент \ (\ left \ langle {u} _ {ck + {e} _ {\ alpha} q} | {u} _ {vk} \ right \ rangle \) изменяется очень медленно, как k -вектор, термин \ (\ left \ langle {u} _ {ck + {e} _ {\ alpha} q} | {u} _ {vk} \ right \ rangle \ left \ langle {u} _ {ck + { e} _ {\ beta} q} | {u} _ {vk} \ right \ rangle \ ast \) в уравнении. (1) можно вынести вне суммирования. В формуле. (1) большая часть дисперсии в \ ({\ varepsilon} _2 ^ {\ alpha \ beta} \ left (\ omega \ right) \) связана с суммированием по дельта-функции δ ( E ck - E вк - ℏ ω ). Это суммирование можно преобразовать в интегрирование по энергии, задав совместную плотность состояний (JDOS) [25, 44],
$$ {J} _ {cv} \ left (\ omega \ right) =\ frac {1} {4 {\ pi} ^ 3} \ int \ frac {dS_k} {\ nabla_k \ left ({E} _ { ck} - {E} _ {vk} \ right)} $$ (5)в котором ℏ ω равно E ck - E вк , S k представляет собой поверхность постоянной энергии, обозначенную E ck - E вк =ℏ ω =Const. Совместная плотность состояний J cv ( ω ) связан с переходами из валентной зоны в зону проводимости, а большие пики в J cv ( ω ) возникнет в спектре, где ∇ k ( E ck - E вк ) ≈ 0. Баллы в k -пространство, где ∇ k ( E ck - E вк ) =0 называются критическими точками или особенностями Ван Хова (VHS), а E ck - E вк называются энергиями критических точек [26, 27]. Критические точки ∇ k E ck =∇ k E вк =0 обычно возникают только в точках высокой симметрии, в то время как критические точки ∇ k E ck =∇ k E вк ≠ 0 может встречаться в любых общих точках зоны Бриллюэна [27, 45]. В двумерном случае есть три типа критических точек, т. Е. P 0 (точка минимума), P 1 (седловая точка) и P 2 (максимальный балл). В точках P 0 или P 2 , особенность ступенчатой функции произошла в JDOS, а в седловой точке P 1 , JDOS описывалась логарифмической особенностью [27]. Более подробно, E c ( к x , k y ) - E v ( к x , k y ) можно разложить в ряд Тейлора о критической точке. Ограничивая разложение квадратичными членами, когда линейный член не возникает из-за свойства особенности, тогда мы имеем
$$ {E} _c \ left ({k} _x, {k} _y \ right) - {E} _v \ left ({k} _x, {k} _y \ right) ={E} _0 + \ frac {\ mathrm {\ hslash}} {2} \ left ({b} _x \ frac {k_x ^ 2} {m_x} + {b} _y \ frac {k_y ^ 2} {m_y} \ right) $$ (6)Таким образом, возникают три типа критических точек. Для P 0 , ( b x > 0, b y > 0), для P 1 , ( b x > 0, b y <0) или ( b x <0, b y > 0), а для P 2 , ( b x <0, b y <0). В этой статье для случая MoS 2 многослойные, только P 0 критическая точка задействована.
На рисунке 6а показаны мнимые части диэлектрической функции \ ({\ varepsilon} _2 ^ {xx} \ left (\ omega \ right) \) MoS 2 . многослойные для E || х. Мы обнаружили интересное явление, что мнимые части диэлектрической проницаемости \ ({\ varepsilon} _2 ^ {xx} \ left (\ omega \ right) \) имеют плато, а плато различных слоев MoS 2 примерно равны в диапазоне 1,75 эВ ~ 2,19 эВ. От пороговой энергии до 1,75 эВ \ ({\ varepsilon} _2 ^ {xx} \ left (\ omega \ right) \) сильно различаются для разных мультислоев MoS 2 . Пороговая и конечная энергии плато в разных слоях различаются, в частности, диапазон энергий \ ({\ varepsilon} _2 ^ {xx} \ left (\ omega \ right) \) плато монослоя значительно шире, чем у других многослойных. Пороговая энергия монослоя MoS 2 диэлектрическая функция равна его прямой запрещенной зоне 1,64 эВ. Однако пороговая энергия двухслойной диэлектрической проницаемости - это не непрямая запрещенная зона 1,17 эВ, а минимум прямой запрещенной зоны 1,62 эВ между валентной зоной и зоной проводимости. Это связано с тем, что мы изучаем только переходы между валентной зоной и зоной проводимости с одним и тем же волновым вектором электрона, которые классифицируются как прямые оптические переходы [36, 47]. По количеству MoS 2 увеличилось до 4 слоев, мы обнаружили, что \ ({\ varepsilon} _2 ^ {xx} \ left (\ omega \ right) \) многослойного MoS 2 системы были почти неотличимы от основной массы. Следовательно, мы подробно обсуждаем здесь только плато монослоя, бислоя и трехслоя, а также объемный MoS 2 . Плато \ ({\ varepsilon} _2 ^ {xx} \ left (\ omega \ right) \) монослоя, двухслойного, трехслойного и объемного MoS 2 закончились при 2,57 эВ, 2,28 эВ, 2,21 эВ и 2,19 эВ соответственно. Чтобы объяснить это более точно, JDOS однослойного, двухслойного, трехслойного и объемного MoS 2 показаны на рис. 7. На рис. 7 также показаны плато в JDOS. Плато однослойного, двухслойного и трехслойного JDOS оканчивается на 2,57 эВ, 2,28 эВ, 2,21 эВ соответственно, что в точности совпадает с таковыми в их \ ({\ varepsilon} _2 ^ {xx} \ left (\ omega \ right ) \). Для массового MoS 2 , плато JDOS закончилось на 2,09 эВ, что немного меньше, чем 2,19 эВ по диэлектрической проницаемости \ ({\ varepsilon} _2 ^ {xx} \ left (\ omega \ right) \).
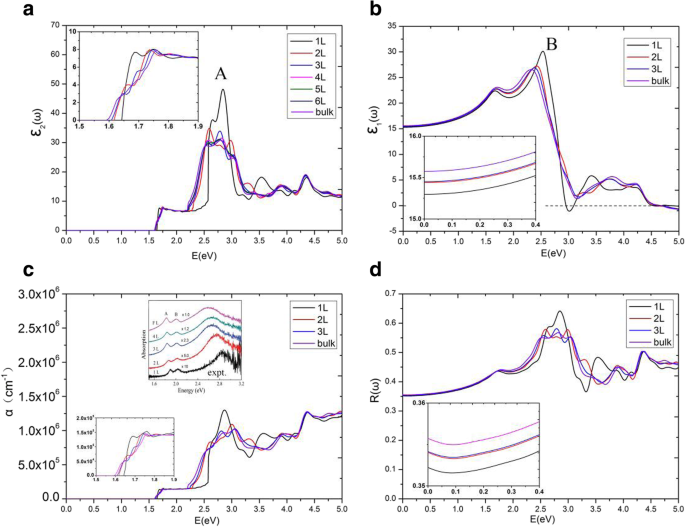
а Мнимые части диэлектрической проницаемости b действительные части диэлектрической проницаемости, c коэффициенты поглощения и d спектры отражения для разного количества MoS 2 слои. Вставка в c также показаны экспериментальные данные [46]
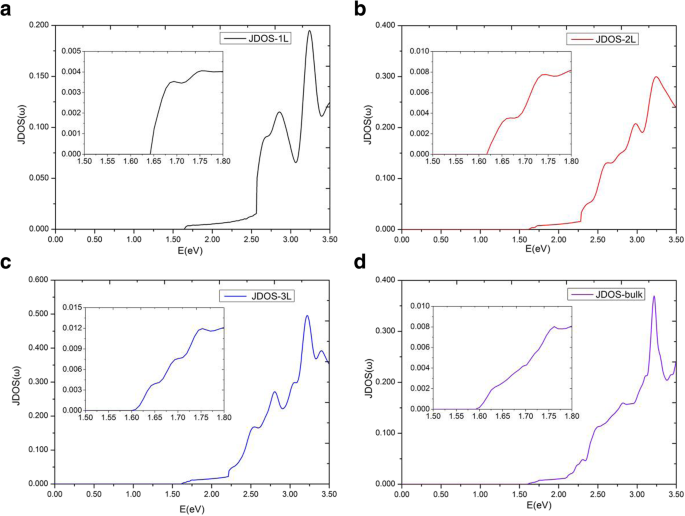
Совместная плотность состояний для монослоя, двухслойного, трехслойного и объемного MoS 2
Для точного анализа электронных переходов и детального анализа диэлектрической проницаемости \ ({\ varepsilon} _2 ^ {xx} \ left (\ omega \ right) \) прямые энергетические зазоры ΔE (NC - NV) между зоны проводимости и валентные зоны монослоя, двухслойного, трехслойного и объемного MoS 2 представлены на рис. 8. Обозначения NC и NV обозначают порядковые номера зон проводимости и валентной зоны. Следовательно, NC =1, 2 и 3 обозначают самый низкий, второй самый низкий и третий самый низкий незанятые полосы материала. С другой стороны, NV =9, 18 и 27 (что зависит от количества электронов в элементарной ячейке) обозначают самую высокую занятую полосу монослоя, двухслойного и трехслойного MoS 2 , соответственно. Для монослоя в области 0 ~ 2,57 эВ обнаружено, что электронные переходы вносят вклад только от самой высокой занятой полосы NV =9 в самую низкую незанятую зону NC =1. Из рис. 8а минимум появляется в точке высокой симметрии. K и порог JDOS (рис. 7a) появляется на уровне 1,64 эВ, который фактически является прямой запрещенной зоной монослоя MoS 2 . Вблизи точки высокой симметрии K кривая ΔE (NC =1 - NV =9) подобна параболе для монослоя MoS 2 . Следовательно, ∇ k ( E ck - E вк ) =0 в точке K, что означает критическую точку в точке высокой симметрии K. В двумерной структуре эта критическая точка принадлежит P 0 особенность типа [27], и поэтому она приводит к ступеньке в JDOS. Таким образом, пороговая энергия плато JDOS находится при энергии критической точки 1,64 эВ. Конечная энергия плато JDOS составляет около 2,57 эВ, что является результатом появления двух P 0 особенности типа в точке B1 ( k =(0.00, 0.16, 0.00)) и точка B2 ( k =(- 0,10, 0,20, 0,00)). Наклоны кривой ΔE (NC =1 - NV =9) вблизи двух критических точек B1 и B2 очень малы, что приводит к быстрому увеличению JDOS (см. Уравнение (5)). Основные критические точки для этих длинных плато JDOS перечислены в таблице 2, включая тип, расположение, переходные полосы и прямую запрещенную зону ΔE (NC - NV). Кроме того, мы обнаружили, что ∇ k E ck =∇ k E вк =0 произошло в точке высокой симметрии K, где наклоны валентной зоны и зоны проводимости горизонтальны. Пока ∇ k E ck =∇ k E вк 0 произошло в точках B1 и B2, что означает, что наклоны двух полос параллельны. Одновременно анализ зонной структуры и прямой запрещенной зоны (см. Рис. 8a) для монослоя показывает, что, когда прямая запрещенная зона ΔE ниже 2,65 эВ, только переходы между NV =9 и NC =1 вносят вклад в JDOS; когда ΔE больше 2,65 эВ, переходы от NV =9 к NC =2 также начинают давать вклад в JDOS; в то время как, когда ΔE достигает значения выше 2,86 эВ, переходы от NV =9 к NC =3 влияют на JDOS. Следует отметить, что для энергии, превышающей 2,65 эВ, многие полосы на рис. 8а будут вносить вклад в JDOS. JDOS однослойного MoS 2 имеет плато в диапазоне 1,64 ~ 2,57 эВ и вариацию выражения | M vc | 2 / ω 2 оказывается малым в этом диапазоне. Согласно уравнениям. (1) и (5) мнимая часть диэлектрической проницаемости \ ({\ varepsilon} _2 ^ {xx} \ left (\ omega \ right) \) в основном определяется JDOS и элементами матрицы перехода, это дает a similar plateau for the imaginary part of dielectric function \( {\varepsilon}_2^{xx}\left(\omega \right) \) as compared to JDOS.
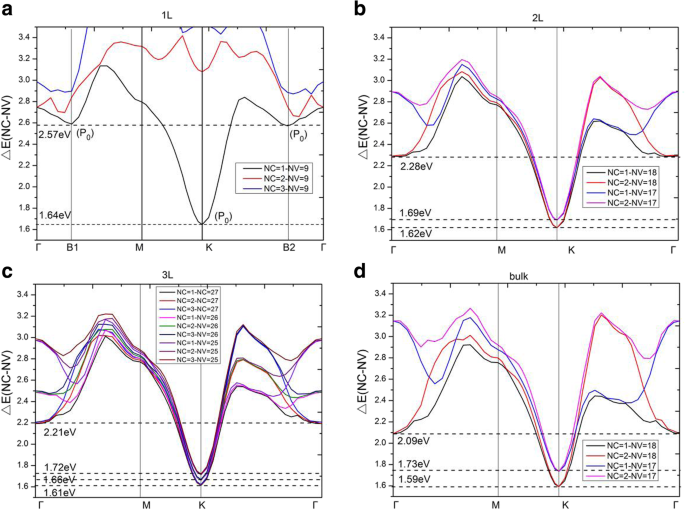
Direct energy gaps, ΔE(NC − NV), between conduction and valence bands for the a monolayer, b bilayer, c trilayer, and d bulk MoS2 . а - г There are three, six, twelve, and six critical points in interband transitions for the monolayer, bilayer, trilayer, and bulk MoS2 соответственно
For bilayer MoS2 , in the region of 0 ~ 2.28 eV (the endpoint of JDOS plateau), the electronic transitions are contributed to NV =17, 18 to NC =1, 2. The minimum energy in ΔE(NC − NV) is situated at the K point with a gap of 1.62 eV. In Fig. 8b, similar to monolayer MoS2 , bilayer MoS2 holds two parabolic curves going upward (which come from ΔE(NC = 1 − NV = 18) and ΔE(NC = 2 − NV = 18)) at K point. Therefore, there are two P 0 type singularities (∇k ( E ck - E vk ) = 0) at K point, causing a step in the JDOS. The critical point energies are both 1.62 eV, this is because that the conduction bands (NC =1 and NC =2) are degenerate at point K (as shown in Fig. 3b), which results in the same direct energy gap between transitions of NV =18 to NC =1 and NV =18 to NC =2. From Fig. 8b, as the direct energy gap is increased to 1.69 eV, two new parabolas (which come from ΔE(NC = 1 − NV = 17) and ΔE(NC = 2 − NV = 17)) appear and two new singularities emerge again at K point in the direct energy gap graph, leading to a new step in JDOS for bilayer MoS2 (see Fig. 7b). As a result, the JDOS of the bilayer MoS2 has two steps around the threshold of long plateau (see inset in Fig. 7b). Two parabolas (in Fig. 8b) contribute to the first step and four parabolas contribute to the second step in JDOS. It means that the value of the second step is roughly the double of the first one. As the ΔE reaches to 2.28eV, two new singularities appear at Γ point (where interband transitions come from Γ(NV =18→NC =1) and Γ(NV =18→NC =2)), which have great contribution to the JDOS and bring the end to the plateau. Our calculations demonstrate that ∇k E ck = ∇k E vk = 0 are satisfied not only at high symmetry point K, but also at high symmetry point Γ. Similar to the case of monolayer, we found that the term of |Mvc | 2 / ω 2 is a slowly varying function in the energy range of bilayer JDOS plateau; hence, \( {\varepsilon}_2^{xx}\left(\omega \right) \) of bilayer have a similar plateau in the energy range.
For trilayer MoS2 , in the region of 0 ~ 2.21 eV, the JDOS are contributed from electronic transitions of NV =25, 26, and 27 to NC =1, 2, and 3. As shown in Fig. 8c, trilayer MoS2 have nine singularities at three different energies (ΔE =1.61 eV, 1.66 eV, and 1.72 eV, respectively) at the K point. Figure 3c depicts that the conduction bands (NC =1, 2, 3) are three-hold degenerate at point K; this means that there are three singularities at each critical point energy. According to our previous analysis, the JDOS and \( {\varepsilon}_2^{xx}\left(\omega \right) \) of trilayer MoS2 will show three steps near the thresholds of the long plateaus, the endpoints of the long plateaus of trilayer JDOS, and \( {\varepsilon}_2^{xx}\left(\omega \right) \) are then owing to the appearance of three singularities at Γ point with ΔE =2.21 eV (see Fig. 7c), which come from the interband transitions of Γ(NV =27→NC =1, 2, 3).
For bulk MoS2 , the thresholds of \( {\varepsilon}_2^{xx}\left(\omega \right) \) and JDOS are also located at K point, with the smallest ΔE(NC − NV) equals to 1.59 eV. Nevertheless, there is no obvious step appeared in the thresholds of plateaus for both the \( {\varepsilon}_2^{xx}\left(\omega \right) \) and JDOS (see Fig. 6a and Fig. 7d). Based on the previous analysis, the number of steps in the monolayer, bilayer, and trilayer MoS2 are 1, 2, and 3, respectively. As the number of MoS2 layers increases, the number of steps also increases in the vicinity of the threshold energy. Thus, in the bulk MoS2 , the JDOS curve is composed of numerous small steps around the threshold energy of the long plateau, and finally the small steps disappear near the threshold energy since the width of the small steps decreases. In the region of 0 ~ 2.09 eV, the electron transitions of bulk MoS2 are contributed to NV =17, 18 to NC =1, 2. The 2.09 eV is the endpoint of JDOS plateau of bulk MoS2 , which is attributed to two singularities, i.e., the interband transitions of Γ(NV =18→NC =1) as well as Γ(NV =18→NC =2), as presented in Fig. 8d. However, the plateau endpoint of the imaginary part of dielectric function \( {\varepsilon}_2^{xx}\left(\omega \right) \) is 2.19 eV, which is greater than the counterpart of JDOS (e.g., 2.09 eV). Checked the transition matrix elements, it verified that some transitions are forbidden by the selection rule in the range of 2.09 eV to 2.19 eV. Therefore, the imaginary part of the dielectric function \( {\varepsilon}_2^{xx}\left(\omega \right) \) is nearly invariable in the range of 2.09 ~ 2.19 eV. As a result, the plateau of \( {\varepsilon}_2^{xx}\left(\omega \right) \) of bulk MoS2 is then 1.59 ~ 2.19 eV.
It has been shown that these thresholds of the JDOS plateaus are determined by singularities at the K point for all of the studied materials, see Fig. 8. The endpoint energy of the monolayer JDOS plateau is determined by two critical points at B1 and B2 (Fig. 8a). Nevertheless, the endpoint energies of bilayer, trilayer, and bulk JDOS plateaus are all dependent on the critical points at Γ(Fig. 8b–d). The interlayer coupling near point Γ is significantly larger than the near point K for all the systems of multilayer MoS2 . The smallest direct energy gap decreases and the interlayer coupling increases as the number of layers grow. With the layer number increases, a very small decrease of direct energy gap at point K and a more significant decrease of direct energy gap at point Γ can be observed, as a result, a faint red shift in the threshold energy and a bright red shift in the end of both JDOS and \( {\varepsilon}_2^{xx}\left(\omega \right) \) plateaus can also be found. For monolayer MoS2 , the smallest ΔE(NC − NV) at point Γ is 2.75 eV which is larger than that at point B1 (or point B2) with a value around 2.57 eV. When it goes to multilayer and bulk MoS2 , the strong interlayer coupling near point Γ makes the smallest ΔE(NC − NV) at Γ less than those at point B1 (or point B2). Hence, monolayer owns the longest plateau of JDOS, which is between 1.64 eV and 2.57 eV. The shortest plateau of JDOS (from 1.59 eV to 2.09 eV) is shown in the bulk.
As the energy is increased to the value larger than the endpoint of long platform of the dielectric function, a peak A can be found at the position around 2.8 eV, for almost all the studied materials (Fig. 6a). The width of peak A for monolayer is narrower compared with those of multilayer MoS2; however, the intensity of peak A for monolayer is found to be a little stronger than multilayers. The differences between the imaginary parts of dielectric function for the monolayer and multilayer MoS2 are evident, on the other hand, the differences are small for multilayer MoS2 .
In order to explore the detailed optical spectra of MoS2 multilayers, the real parts of the dielectric function ε 1 ( ω ), the absorption coefficients α ( ω ), and the reflectivity spectra R ( ω ) are presented in Fig. 6b–d. Our calculated data of bulk MoS2 for the real and imaginary parts of the dielectric function, ε 1 ( ω ) and ε 2 ( ω ), the absorption coefficient α ( ω ) and the reflectivity R ( ω ) agree well with the experimental data, except for the excitonic features near the band edge [48,49,50]. The calculated values of 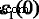 , which is called the static dielectric constant, for MoS2 multilayers and bulk can be found in Table 1. From Table 1, the calculated values of \( {\varepsilon}_1^{xx}(0) \) for multilayers and bulk MoS2 are all around 15.5, which is very close to the experimental value of 15.0 for bulk MoS2 [50]. The values of \( {\varepsilon}_1^{xx}(0) \) increase with the increasing number of MoS2 layers. For monolayer MoS2 , a clear peak B of \( {\varepsilon}_1^{xx}\left(\omega \right) \) appears about 2.54 eV. Peak B of monolayer is clearly more significant than multilayers, and they are all similar for multilayer MoS2 . As the layer number increases, the sharp structures (peak B) also move left slightly. In Fig. 6c, we also observe the emergence of long plateaus in the absorption coefficients, and absorption coefficients are around 1.5 × 10
5
см
−1
at the long plateaus. There are also small steps around the thresholds for the absorption coefficients, which are consistent to those of the imaginary parts of dielectric function. With the layer number increases, the threshold energy of absorption coefficient decreases, while the number of small steps increases at the starting point of the plateau. For monolayer and multilayer MoS2 , strong absorption peaks emerge at visible light range (1.65–3.26 eV), and the monolayer MoS2 own a highest absorption coefficient of 1.3 × 10
6
см
−1
. The theoretical absorption coefficients for different number of MoS2 layers are compared with confocal absorption spectral imaging of MoS2 (the inset) [46], as shown in Fig. 6c. For monolayer and multilayer MoS2 , a large peak of α ( ω ) can be found at the position around 2.8 eV for both the calculation and experiment [46, 51]. Furthermore, a smoothly increase of α ( ω ) can be found between 2.2 and 2.8 eV for both the theoretical and experimental curves. Therefore, from Fig. 6c, the calculated absorption coefficients of MoS2 multilayers show fairly good agreement with the experimental data [46], except for the excitonic peaks. The reflectivity spectra are given in Fig. 6d. The reflectivity spectra of MoS2 multilayers are all about 0.35–0.36 when energy is zero, which means that MoS2 system can reflect about 35 to 36% of the incident light. In the region of visible light, the maximum reflectivity of monolayer MoS2 is 64%, while the maxima of multilayer and bulk MoS2 are all about 58%. Because of the behaviors discussed, MoS2 monolayer and multilayers are being considered for photovoltaic applications.
, which is called the static dielectric constant, for MoS2 multilayers and bulk can be found in Table 1. From Table 1, the calculated values of \( {\varepsilon}_1^{xx}(0) \) for multilayers and bulk MoS2 are all around 15.5, which is very close to the experimental value of 15.0 for bulk MoS2 [50]. The values of \( {\varepsilon}_1^{xx}(0) \) increase with the increasing number of MoS2 layers. For monolayer MoS2 , a clear peak B of \( {\varepsilon}_1^{xx}\left(\omega \right) \) appears about 2.54 eV. Peak B of monolayer is clearly more significant than multilayers, and they are all similar for multilayer MoS2 . As the layer number increases, the sharp structures (peak B) also move left slightly. In Fig. 6c, we also observe the emergence of long plateaus in the absorption coefficients, and absorption coefficients are around 1.5 × 10
5
см
−1
at the long plateaus. There are also small steps around the thresholds for the absorption coefficients, which are consistent to those of the imaginary parts of dielectric function. With the layer number increases, the threshold energy of absorption coefficient decreases, while the number of small steps increases at the starting point of the plateau. For monolayer and multilayer MoS2 , strong absorption peaks emerge at visible light range (1.65–3.26 eV), and the monolayer MoS2 own a highest absorption coefficient of 1.3 × 10
6
см
−1
. The theoretical absorption coefficients for different number of MoS2 layers are compared with confocal absorption spectral imaging of MoS2 (the inset) [46], as shown in Fig. 6c. For monolayer and multilayer MoS2 , a large peak of α ( ω ) can be found at the position around 2.8 eV for both the calculation and experiment [46, 51]. Furthermore, a smoothly increase of α ( ω ) can be found between 2.2 and 2.8 eV for both the theoretical and experimental curves. Therefore, from Fig. 6c, the calculated absorption coefficients of MoS2 multilayers show fairly good agreement with the experimental data [46], except for the excitonic peaks. The reflectivity spectra are given in Fig. 6d. The reflectivity spectra of MoS2 multilayers are all about 0.35–0.36 when energy is zero, which means that MoS2 system can reflect about 35 to 36% of the incident light. In the region of visible light, the maximum reflectivity of monolayer MoS2 is 64%, while the maxima of multilayer and bulk MoS2 are all about 58%. Because of the behaviors discussed, MoS2 monolayer and multilayers are being considered for photovoltaic applications.
Выводы
In this study, by employing ab initio calculations, the electronic and optical properties of MoS2 multilayers are investigated. Compared to bulk MoS2 , the covalency and ionicity of monolayer MoS2 are found to be stronger, which results from larger quantum confinement in the monolayer. With the increase of the layer number, quantum confinement and intra-layer interaction both decrease, meanwhile, the interlayer coupling increases, which result in the decrease of the band gap and the minimum direct energy gap. As the layer number becomes larger than two, the optical and electronic properties of MoS2 multilayers start to exhibit those of bulk. Band structures of multilayers and bulk show splitting of bands mainly around the Γ-point; however, splitting of bands in the vicinity of K point are tiny, owing to the small interlayer coupling at point K.
For optical properties, Van Hove singularities lead to the occurrence of long plateaus in both JDOS and \( {\varepsilon}_2^{xx}\left(\omega \right) \). At the beginnings of these long plateaus, monolayer, bilayer, and trilayer structures appear one, two, and three small steps, respectively. With the layer number increases, the number of small steps increases and the width of the small steps decreases, leading to unobvious steps. A small red shift in the threshold energy and a noticeable red shift in the end of both JDOS and \( {\varepsilon}_2^{xx}\left(\omega \right) \) plateaus are observed, since the increased number of layers leads to small changes in the direct energy gap near point K (weak interlayer coupling) and larger changes near point Γ (stronger interlayer coupling). Thus, the longest plateau and shortest plateau of JDOS are from the monolayer and bulk, respectively. Our results demonstrate that the differences between electronic and optical properties for monolayer and multilayer MoS2 are significant; however, the differences are not obvious between the multilayer MoS2 . The present data can help understand the properties of different layers of MoS2 , which should be important for developing optoelectronic devices.
Доступность данных и материалов
Наборы данных, подтверждающие выводы этой статьи, включены в статью.
Сокращения
- Δ E:
-
The direct energy gap
- 1L:
-
Monolayer MoS2
- 2L:
-
Bilayer MoS2
- 3L:
-
Trilayer MoS2
- 4L:
-
Four-layer MoS2
- 5L:
-
Five-layer MoS2
- 6L:
-
Six-layer MoS2
- BSE:
-
Bethe-Salpeter equation
- BZ:
-
Brillouin zone
- CBM:
-
Минимальная зона проводимости
- GGA:
-
Обобщенное приближение градиента
- GW:
-
Quasi-particle energy calculation
- JDOS:
-
Joint density of states
- MoS 2 :
-
Дисульфид молибдена
- NC:
-
The ordinal numbers of conduction band
- NV:
-
The ordinal numbers of valence band
- PAW:
-
Projector augmented wave
- PBE:
-
Perdew-Burke-Ernzerhof
- VASP:
-
Пакет для моделирования в Вене ab initio
- VBM:
-
Максимальный диапазон валентности
- VHS:
-
Van Hove singularity
Наноматериалы
- Раскрытие атомной и электронной структуры углеродных нановолокон с набором чашек
- Структура и электронные свойства наноглины каолинита, легированной переходным металлом
- Модуляция свойств электронной и оптической анизотропии ML-GaS вертикальным электрическим полем
- Легкий синтез и оптические свойства малых нанокристаллов и наностержней селена
- Влияние толщины бислоя на морфологические, оптические и электрические свойства наноламинатов Al2O3 / ZnO
- Оптические и электронные свойства фемтосекундных лазерно-индуцированных гипердопированных серой кремниевы…
- Исследование структурных, электронных и магнитных свойств кластеров Ag n V (n =1–12)
- Зависимость токсичности наночастиц от их физических и химических свойств
- Оптические свойства пленок ZnO, легированных алюминием, в инфракрасной области и их применения для поглощения
- Монослой g-GaN, адсорбированный щелочными металлами:сверхнизкие работы выхода и оптические свойства



