Влияние деформации на термоэлектрические характеристики монослоя InSe

Введение

Двумерные (2D) полупроводниковые материалы привлекают внимание исследователей для изучения их удивительных свойств и полезного применения с момента открытия графена. В частности, было обнаружено, что семейство двумерных халькогенидов металла демонстрирует большой потенциал в наноэлектронике и нанофотонике благодаря своим необычным электронным, оптическим и механическим свойствам [1,2,3,4]. В последнее время селенид индия (InSe), слоистое соединение металл-халькогенид III-VI групп, представляет большой интерес как экспериментально, так и теоретически. Сообщалось, что атомный слой InSe успешно синтезирован физическими [5,6,7,8,9,10] и химическими методами [11,12,13,14], а также применением нанолиста InSe на сенсорах [15] , оптоэлектроника и фотоприемники. Шриниваса и др. сообщил о создании многослойных фотоприемников InSe с высокой чувствительностью и широким спектральным детектированием от видимой до ближней инфракрасной области [6]. Бандурин и др. обнаружили качественный двумерный электронный газ в многослойном InSe с подвижностями носителей 10 ³ и 10 ⁴ см ² / Vs при комнатной температуре и температуре жидкого гелия [16]. Wei et al. обнаруженные многослойные полевые транзисторы из InSe с обратным затвором демонстрируют сверхвысокую подвижность носителей до 1055 см ² / Vs при комнатной температуре из-за подавленного рассеяния носителей заряда на диэлектрической подложке [5].

2D InSe имеет довольно необычную зонную структуру, которая представляет собой комбинацию плоской зоны наверху валентной зоны и параболической зоны внизу зоны проводимости, демонстрируя, таким образом, высокие термоэлектрические характеристики [17]. В частности, термоэлектрические характеристики могут быть описаны безразмерным показателем добротности, ZT , определяемый как ZT =S ² Tσ / ( Κ _e + Κ _l ), где S эффективен ли Зеебек, T абсолютная температура, σ - электропроводность, а Κ _e и Κ _l - теплопроводность с вкладами электронных носителей и решетки соответственно. Теплопроводность решетки K _l отношение к фононным транспортным свойствам играет важную роль для определения термоэлектрических характеристик. Предыдущие зарегистрированные K _l монослоя InSe намного меньше, чем у графена, в то время как он был в 10 раз больше, чем у листа SnSe [18, 19].

Высокий уровень подвижности электронов и низкая теплопроводность благоприятно сказываются на термоэлектрических характеристиках. Кроме того, однослойный InSe демонстрирует превосходную механическую гибкость, а его электронные свойства можно непрерывно модулировать умеренной деформацией в широком диапазоне [20,21,22]. Было продемонстрировано, что коэффициент термоэдс монослоя InSe может быть значительно увеличен за счет сходимости зон при деформации сжатия [23]. Для термоэлектрических материалов деформация при растяжении также может вызывать изменение зонной структуры и свойств теплопереноса. Однако зависимость теплопередающих свойств от деформации непредсказуема и тесно связана с конкретным материалом и кристаллической структурой. В этой статье настоящая работа выполняется на эффекте двухосной деформации растяжения для термоэлектрических характеристик монослоя InSe с помощью расчетов из первых принципов, включая электронные и фононные транспортные свойства. Из-за повышенного ангармонического рассеяния определено положительное влияние деформации растяжения на термоэлектрические характеристики монослоя InSe.

Методология

Расчет структурных и электронных свойств монослоя InSe выполняется на основе теории функционала плотности (DFT), реализованной в пакете для моделирования Vienna ab initio (VASP) [24,25,26]. Для обменно-корреляционного функционала мы выбрали метод проекционно-дополненных волн с приближением локальной плотности (LDA) [27,28,29]. И вакуум 12 Å по z -ось используется, чтобы избежать взаимодействия между периодическими изображениями плит. K-сетки Монкхорста-Пак 21 × 21 × 1 и 31 × 31 × 1 использовались при расчетах структурной релаксации и электронной структуры элементарной ячейки. Энергетическая обрезка базиса плоских волн была установлена ​​равной 500 эВ. Критерий сходимости для полной энергии был установлен как 10 ⁻⁴ эВ, и все положения атомов и структуры решетки были полностью расслаблены с допуском силы 10 ⁻³ эВ / Å.

Термоэлектрические транспортные свойства могут быть получены в рамках приближения постоянного времени релаксации по теории Больцмана, реализованной в программе BoltzTraP [30, 31]. В этом приближении коэффициенты электронного переноса можно определить как

где Ω - объем элементарной ячейки, f _μ - функция распределения Ферми-Дирака, а α и β - тензорные индексы. Функция распределения транспорта ∑ _αβ ( ε ) дается

где N ₀ указывает количество q отобранных точек, i это индекс полосы, v - групповая скорость носителей, а τ время релаксации.

Пакет ShengBTE [32] используется для решения фононного уравнения переноса Больцмана и определения тепловых и других параметров решетки. Суперячейка 5 × 5 × 1 используется для расчета гармонических межатомных силовых констант с помощью расчета теории возмущений функционала плотности (DFPT) [33]. А метод конечных разностей используется для вычисления ангармонических межатомных силовых постоянных с суперячейкой 4 × 4 × 1 [34]. Фононный спектр был рассчитан с помощью программы Phonopy [35].

Результат и обсуждение

Монослой InSe представляет собой четырехатомный лист с ковалентным связыванием Se-In-In-Se в один слой. Сверху монослой представляет собой сотовую решетку, и каждый атом Se связан с другими тремя атомами In, как показано на рис. 1a. На основе минимизации полной энергии параметры решетки этого кристалла рассчитываются как a ₀ =3,95 Å. В этой статье мы используем двухосную деформацию монослоя InSe, сохраняя симметрию кристалла, изменяя его решетку как δ =( а - а ₀ ) / а ₀ × 100%, где a и a ₀ - постоянная решетки монослоя InSe при деформации и без деформации соответственно. Когда двухосная деформация растяжения накладывается на монослой InSe, длина связи d _InSe монотонно увеличиваются с увеличением деформации, и это приводит к увеличению угла связи In-Se-In (см. рис. 1b).

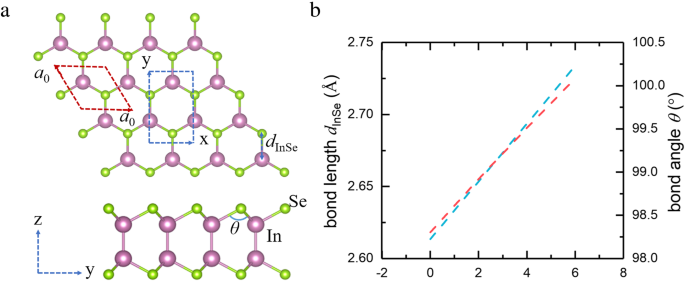
а Монослой InSe, вид сверху и сбоку. Розовые и зеленые шары представляют собой атомы In и Se соответственно. б Изменение длины связи и угла связи с увеличением двухосной деформации растяжения. Базовый a ₀ × а ₀ элементарная ячейка и x × г суперячейки монослоя InSe обозначены красными и синими пунктирными линиями соответственно

Монослой InSe представляет собой непрямой полупроводник с шириной запрещенной зоны 1,67 эВ, где минимум зоны проводимости (CBM) существует в точке Г, а точки максимума валентной зоны (VBM) находятся между точками Г и K, как показано на рис. 2a. Валентная зона монослоя InSe демонстрирует дисперсию мексиканской шляпы, которая также может быть обнаружена во многих двумерных материалах [36,37,38,39]. Модификация зонной структуры в ответ на растягивающую деформацию была исследована на рис. 2, и три экстремума зоны проводимости обозначены символами I, II и III соответственно. При растяжении зона проводимости с наименьшей энергией чувствительна к деформации и смещается вниз, в то время как валентная зона почти остается постоянной, что приводит к уменьшению ширины запрещенной зоны. Без деформации между вторым и третьим минимумом зоны проводимости есть мельчайшие различия, а впадины зон имеют тенденцию к конвергенции. Однако с увеличением деформации растяжения разница в энергии постепенно увеличивается. Мы также сравнили ширину запрещенной зоны при различных деформациях с соответствующими теоретическими и экспериментальными результатами, как подробно описано в Дополнительном файле 1:Таблица S2.

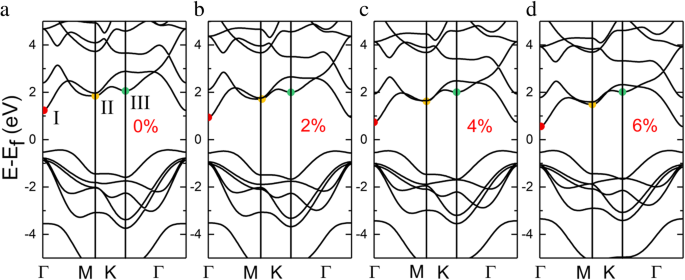
Зонная структура монослоя InSe при различных условиях деформации

Влияние деформации растяжения на термоэлектрические коэффициенты переноса

На основе рассчитанной электронной структуры мы проводим расчеты коэффициента термоэлектрического переноса по полуклассической теории Больцмана. По времени рассеяния τ , Коэффициент Зеебека S , и электропроводность σ можно рассчитать. На рис. 3а показана рассчитанная зависимость коэффициента Зеебека от уровня Ферми. Для простоты часто предполагается, что зонная структура остается неизменной от легирования при конечных температурах [40, 41], а влияние легирования на коэффициент термоэлектрического переноса может быть получено путем изменения положения уровня Ферми. Отрицательный ε _f указывает на легирование p-типа, перемещая уровень Ферми в валентную зону, и может быть получен положительный коэффициент Зеебека. Точно так же положительное ε _f дала отрицательный коэффициент Зеебека. Можно найти, что полученный результат без деформации очень близок к предыдущему отчету [17], а максимум коэффициента Зеебека уменьшается с увеличением деформации растяжения, что связано с изменением ширины запрещенной зоны [42].

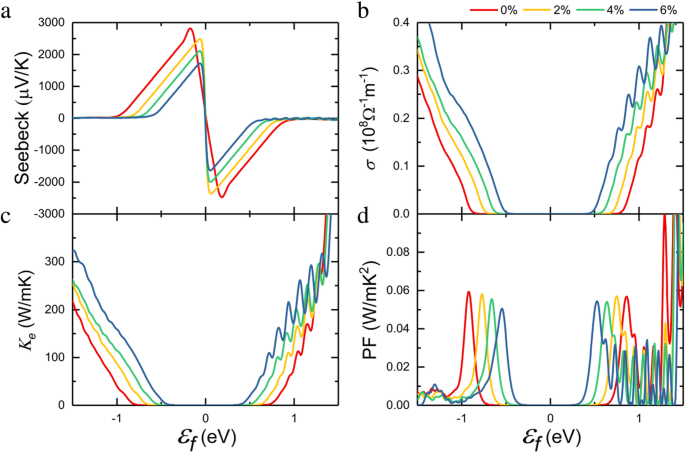
а Коэффициент Зеебека, b электропроводность, c электронная теплопроводность, d коэффициент мощности монослоя InSe в зависимости от химического потенциала при 300 K при приложении различной двухосной деформации

Для расчета электропроводности σ , время релаксации τ требуется, потому что на выходе будет σ / τ в коде BoltzTraP. Здесь τ определяется

где μ мобильность носителя и м * - эффективная масса. В теории потенциала деформации подвижность носителей в 2D-материалах может быть рассчитана по [43, 44]

Здесь e - заряд электрона, ℏ - постоянная Планка, и k _B - постоянная Больцмана. C представляет модуль упругости и может быть рассчитан с помощью C =( ∂ ² E / ∂δ ² ) / S ₀ , где E , δ , и S ₀ - полная энергия, приложенная деформация и площадь равновесия для 2D-системы соответственно. E ₁ постоянная потенциала деформации, обозначенная как E ₁ = ΔE _край / Δδ , где ΔE _край - изменение энергии краев зоны. м _d - средняя эффективная масса, полученная из \ ({m} _d =\ sqrt {m_x ^ {\ ast} {m} _y ^ {\ ast}} \). Чтобы вычислить подвижность, прямоугольник x × г суперячейка принята, как показано на рис. 1а. Полученное значение C вдоль x ( г ) направление составляет 60,43 Н / м (53,68 Н / м), что получается путем аппроксимации кривой зависимости энергии от деформации, как показано в Дополнительном файле 1:Рисунок S1. Расчетный потенциал деформации E ₁ составляет 6,13 эВ (6,14 эВ) для электрона вдоль x ( г ) направлении и 3,45 эВ (3,33 эВ) для дырки вдоль x ( г ) направление. Результаты расчетов эффективной массы, подвижности носителей заряда и времени релаксации для монослоя InSe при разной деформации сведены в Таблицу 1. Мы можем обнаружить, что разница между различными направлениями небольшая, а эффективная масса и подвижность носителей в целом изотропны. Поэтому мы используем среднее значение x и y инструкции для оценки термоэлектрических характеристик позже. Эффективные массы дырок увеличиваются за счет приложенной деформации, в то время как эффективные массы для электрона почти не меняются. С рассчитанным временем релаксации, электропроводность может быть получена при заданном химическом потенциале на рис. 3b. Видно, что удельная электропроводность σ увеличиваются с увеличением деформации растяжения в системе с сильным легированием p-типа из-за увеличения подвижности дырок, тогда как σ остается относительно низким при низком уровне легирования. Более того, тенденция электронной теплопроводности согласуется с электрической проводимостью в соответствии с законом Видемана-Франца: K _e = LσT на рис. 3c, где L это число Лоренца. Коэффициент мощности можно получить как PF = S . ² σ / τ , который определяет, сколько электроэнергии может быть произведено. Учитывая общую тенденцию коэффициента Зеебека и электропроводности, деформация растяжения немного снижает коэффициент мощности, как показано на рис. 3d.

Влияние деформации при растяжении на Κ _l

В металлах электроны ответственны за теплоносители, тогда как в полупроводниках и диэлектрических твердых телах, где легирование и температура не очень высоки, колебания решетки будут основной причиной переноса энергии [45]. Теплопроводность решетки - очень важный параметр для термоэлектрических применений. С теоретической точки зрения и в простом приближении теплопроводность решетки Κ _l можно выразить следующим образом [46,47,48]:

где C _λ , v _λ , и V - теплоемкость, групповая скорость фононов и объем кристалла соответственно. τ _λ - время релаксации моды λ, которое можно оценить с помощью правила Маттиссена [49]:

где \ (\ frac {1} {\ tau _ {\ uplambda} ^ b} \) - граничная скорость рассеяния, \ (\ frac {1} {\ tau _ {\ uplambda} ^ {\ mathrm {iso}}} \ ) - скорость изотропного примесного рассеяния, а \ (\ kern0.1em \ frac {1} {\ tau _ {\ uplambda} ^ {3 \ mathrm {ph}}} \) - скорость трехфононного рассеяния.

На рисунке 4a представлены Κ _l изменение монослоя InSe с температурой при различной деформации. Решеточная теплопроводность в бездеформационном случае составляет 25,9 Вт / мК при комнатной температуре, что сопоставимо с предыдущим отчетом [19]. При увеличении приложенной деформации до 6% теплопроводность решетки снизилась до 13,1 Вт / мК, что подтверждает, что инженерия деформации является очень эффективным методом изменения теплопроводности решетки. Мы построили соответствующую кривую дисперсии фононов монослоя InSe для различных деформаций на рис. 4c, чтобы определить причину уменьшения теплопроводности решетки. Он содержит 12 фононных мод, поскольку монослой InSe имеет четырехатомную элементарную ячейку. В фононных спектрах отсутствует отрицательная частота, что подтверждает термическую стабильность монослоя InSe. Три ветви, начинающиеся с 0 в области низких энергий на кривой дисперсии фононов, равны z -осевой акустический (ZA), продольный акустический (LA) и поперечный акустический (TA), соответственно, а остальные являются оптическими модами. С увеличением деформации растяжения квадратичный характер ZA-моды превращается в почти прямую в области низких энергий. Тенденцию к снижению частоты оптических мод можно наблюдать при деформации растяжения, поскольку деформация растяжения ослабляет связи, а затем приводит к более низким частотам. Мы также обсуждаем вклад каждой фононной ветви в Κ _l для недеформированного монослоя InSe с деформацией 6% на рис. 4б. В состоянии без деформации режим ZA вносит значительный вклад в перенос тепла, а когда к монослою InSe прикладывается 6% -ная деформация растяжения, относительный вклад моды ZA снижается с 58 до 38%. По мере увеличения деформации растяжения режим ZA становится более жестким, что приводит к уменьшению вклада в Κ _l .

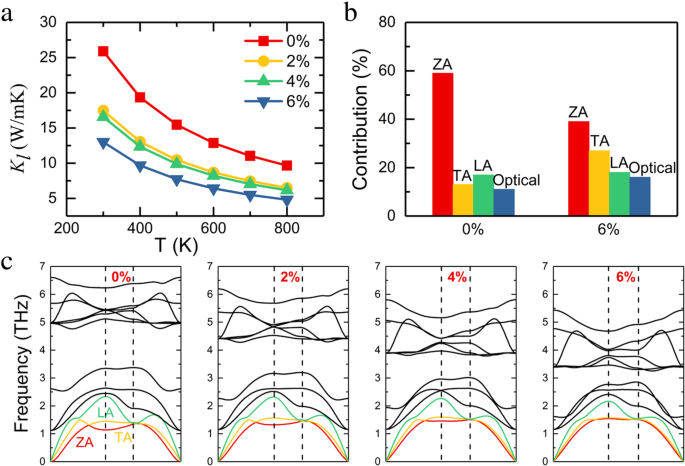
а Расчетное влияние двухосной деформации на теплопроводность решетки при различных температурах. б Вклад ZA, TA, LA и всех оптических ветвей в теплопроводность решетки для недеформированных и 6% деформированных систем. c Кривые фононной дисперсии монослоя InSe для различных деформаций

Далее представлен подробный анализ изменения групповой скорости фононов, вызванного деформацией растяжения, чтобы понять свойства переноса фононов. Для плоских акустических мод групповые скорости фононов уменьшаются при деформации 6%, как показано на рис. 5a, b. В сочетании с повышенным вкладом LA и TA снижение групповой скорости фононов играет жизненно важную роль в уменьшении Κ _l . Изменение групповых скоростей фононов происходит из-за изменения структуры, вызванной деформацией:при включении деформации растяжения расстояние связи увеличивается, а прочность связи уменьшается, что приводит к снижению частоты фононов и групповой скорости. Учитывая, что три ветви акустических фононов вносят основной вклад в Κ _l , повышенные групповые скорости фононов оптических ветвей имеют ограниченный эффект.

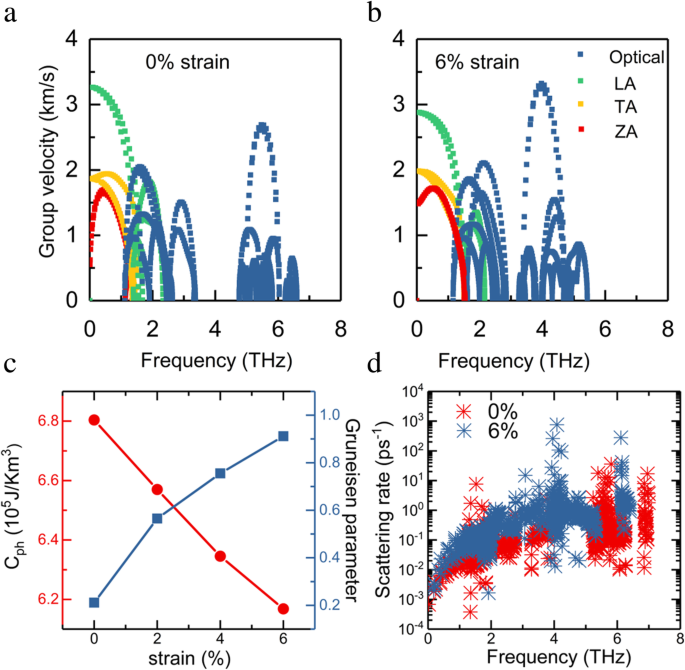
Вклад ZA, TA, LA и оптических мод в групповую скорость монослоя InSe для ( a ) без напряжения и ( b ) 6% напряженных систем. c Фононная теплоемкость ( C _ph ) и параметр Грюнайзена как функция деформации при 300 К. d Зависимость скорости рассеяния фононов недеформированного и 6% напряженного монослоя InSe от частоты.

Скорость трехфононного рассеяния монослоя InSe без деформации и с 6% -ной деформацией как функция частоты показана на рис. 5d. Можно заметить, что скорость трехфононного рассеяния 6% -ного деформированного монослоя InSe в области более низких частот значительно выше, чем у ненапряженного случая, что указывает на то, что увеличение напряжения приводит к более сильному трехфононному рассеянию. Повышенное трехфононное рассеяние в основном отвечает за понижение решеточной теплопроводности, что также согласуется с предыдущим выводом [19]. Аналогичная тенденция скорости рассеяния фононов с увеличением деформации растяжения наблюдалась в ZrS ₂ и 2H MoTe ₂ монослой [50, 51]. Мы также проанализировали влияние двухосной деформации растяжения на теплоемкость фононов ( C _ph ), как показано на рис. 5в. С увеличением деформации растяжения фононная теплоемкость монослоя InSe монотонно уменьшается. Для системы с напряжением 6% фононная теплоемкость снижается до 6,2 × 10 ⁵ Дж / км ³ . Из-за линеаризации и усиления ZA-моды плотность фононных состояний уменьшается, что приводит к уменьшению фононной теплоемкости. Параметры Грюнайзена предоставляют информацию об ангармоничности системы и могут быть получены из ангармонических межатомных силовых констант (IFC) [32, 52]. На рис. 5в показаны рассчитанные параметры Грюнайзена при различных деформациях. Повышенный параметр Грюнайзена, вызванный деформацией растяжения, означает более сильный ангармонизм, что приводит к более низкой теплопроводности [18].

При всех доступных термоэлектрических транспортных свойствах можно получить добротность ZT. Приложенная деформация растяжения по-разному влияет на эти транспортные свойства, и улучшение термоэлектрических характеристик монослоя InSe требует сложного баланса между этими параметрами S , σ , и κ . На рисунке 6 показана рассчитанная добротность с различной деформацией как функция химического потенциала при 300 К, и очевидно, что изменение значения ZT при разных деформациях сильно зависит от химического потенциала, а максимальное значение ZT может быть эффективно увеличено с помощью повышение напряжения. Без деформации монослой InSe имеет максимальное значение ZT 0,36 при комнатной температуре, что близко к таковому у силицена (0,36), германена (0,41) и однослойного MoS ₂ (0,58) [53, 54] и ниже, чем у 2D-монохалькогенидов (1,29 ~ 2,63 при 700 K) [55]. Учитывая высокую подвижность носителей и превосходную механическую гибкость, напряженный монослой InSe также является многообещающим потенциальным материалом для термоэлектрических применений. При приложении растягивающей деформации ослабленная межатомная связь вызывает более сильный ангармонизм. Повышенная скорость рассеяния фононов, уменьшенная групповая скорость фононов и фононная теплоемкость вместе привели к снижению теплопроводности решетки, что привело к увеличению добротности. Предыдущие теоретические расчеты показали, что монослой InSe может выдерживать деформацию растяжения более 20%, что намного больше, чем наши предсказанные деформации [20]. В эксперименте приложение деформации к 2D-материалам в основном происходит из-за их взаимодействия с подложкой, которое может быть вызвано нагревом [56], рассогласованием решеток между эпитаксиальными тонкими пленками [57] или изгибом 2D-материала на подложке [58, 59]. Фактически, экспериментально чаще применяется одноосная деформация вместо двухосной деформации. Основываясь на предыдущих отчетах [20], одноосная деформация может демонстрировать аналогичное улучшение термоэлектрических свойств монослоя InSe.

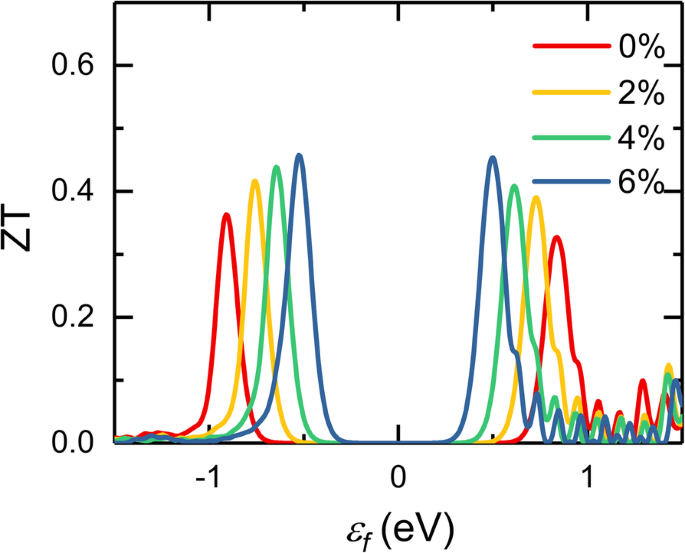
Расчетная добротность монослоя InSe как функция химического потенциала при различных деформациях

Заключение

В заключение мы систематически исследуем возможное влияние двухосной деформации растяжения на электронные, термоэлектрические и фононные транспортные свойства монослоя InSe с помощью расчетов из первых принципов. Ширина запрещенной зоны уменьшается по мере увеличения деформации растяжения, что приводит к уменьшению коэффициента Зеебека. Растягивающая деформация также вызывала более сильное ангармоническое рассеяние, и уменьшение решеточной теплопроводности могло быть связано с результирующим увеличением скорости рассеяния фононов, уменьшением групповой скорости фононов и теплоемкости фононов. Уменьшение теплопроводности решетки перевешивает снижение коэффициента Зеебека, что приводит к улучшенным характеристикам с увеличением деформации растяжения.

Доступность данных и материалов

Наборы данных, созданные и / или проанализированные в ходе текущего исследования, доступны по запросу у соответствующего автора.

Сокращения

2D:

Двумерный

CBM:

Минимальная зона проводимости

τ :

Время релаксации

C _ph :

Фононная теплоемкость

FET:

Полевой транзистор

Лос-Анджелес:

Продольная дисперсия акустических фононов

PF:

Коэффициент мощности

S :

Коэффициент Зеебека

TA:

Поперечная дисперсия акустических фононов

VBM:

Максимальный диапазон валентности

ZA:

г -осевая дисперсия акустических фононов

ZT:

Достоинства

ε _f :

Уровень Ферми

Κ _e :

Коэффициент теплопроводности с учетом вкладов электронных носителей

Κ _l :

Коэффициент теплопроводности с учетом решетки

σ :

Электропроводность