Плазмонный резонанс при фотопоглощении коллоидных высоколегированных нанокристаллов ZnO

Фон

Во многом оптические свойства наночастиц определяются наличием в их спектрах возбуждения локализованных поверхностных плазмонных резонансов (ЛППР) [1–8]. Kriegel et al. [2] опубликовали довольно подробный обзор возникающих коллоидных нанокристаллов (НК), включая НК оксидов металлов, легированных примесью, НК халькогенидов меди и НК вырожденно легированных полупроводников, и подробно обсудили их оптические свойства, а также приложения для зондирования ближнего поля. совершенствование спектроскопии, перестраиваемых оптоэлектронных устройств или биомедицинских приложений. Все эти новые материалы являются альтернативой НК благородных металлов, которые широко изучались в течение последних десятилетий; для всестороннего обзора см. также Ref. [9]. Было показано, что можно регулировать оптический отклик сильно легированных полупроводниковых нанокристаллов (НК) вплоть до ИК-диапазона [10–15], воздействуя на различные управляющие параметры [11, 13, 16–20], тем самым открывая новые перспективы нанофотоники. Основное преимущество полупроводниковых НК состоит в том, что плотность носителей можно регулировать в широком интервале. В то время как металлический проводник имеет фиксированную плотность электронов, полупроводник можно легировать для достижения произвольной плотности носителей в диапазоне 10 ¹⁶ ÷ 10 ²² см ⁻³ [10, 13, 21, 22]. Легирование носителем позволяет получить доступ к настраиваемому LSPR в широком диапазоне частот от ТГц до ИК и видимой области [13]. Такая перестраиваемость плотности носителей является уникальным свойством полупроводниковых наночастиц и не может быть достигнута с помощью металлических капель [23–25]. Легирование может быть выполнено путем включения различных типов примесей в кристаллическую решетку [7, 10, 18], а частота плазмонного резонанса может быть настроена или переключена путем активного управления носителями [13, 16–18, 21, 22]. Более того, частота плазмона и форма его линии зависят не только от плотности носителей НК, но и от типа легирования, которое может быть «объемным» или «поверхностным» [15, 22]. В первом случае заряд свободных носителей нейтрализуется зарядом легирующих примесей по всему объему НК, а во втором случае свободные носители инжектируются в объем НК донорами / акцепторами из окружающих сред, расположенных в Интерфейс ЧПУ.

Теоретические исследования оптического отклика полупроводниковых наночастиц выявили существенные различия между квантово-механическими и классическими описаниями [5, 22, 24, 26]. По мере уменьшения размера наночастиц плазмонный резонанс смещается в область более высоких энергий с видимым отклонением от классических предсказаний [5, 21, 22]. Более того, динамические свойства высоколегированных НК претерпевают переход от режима размерного квантования к классическому режиму плазмонных колебаний [22]. Это можно наблюдать, варьируя количество несущих или размер NC.

В этой работе мы представляем теоретический анализ оптического отклика фотодегированных НК ZnO, экспериментально исследованных в [4]. [21, 27]. В этих экспериментальных исследованиях были измерены сечения фотопоглощения коллоидных НК ZnO фиксированных размеров и плотностей носителей. Фотоэлектроны зоны проводимости генерировались в НК ZnO путем фотодопирования, в то время как дырки захватывались центрами поглощения дырок в окружающем толуоле. Средняя концентрация проводящих электронов n _e в почти сферических фотодопированных нанокристаллах разного радиуса (от 1,75 до 6 нм) достигала верхнего предела (1,4 ± 0,4) × 10 ²⁰ см ⁻³ [21, 27]. Внутриполосное поглощение измерялось в диапазоне от 0,2 до 1,0 эВ, и наблюдались значительные различия с предсказанием классической модели Друде. Авторы показали, что квантово-механический подход, основанный на одночастичных переходах, дал экспериментальную размерную зависимость резонансной частоты только качественно [21].

Целью данной статьи является пересмотр теоретического подхода к плазмонным резонансам в фотодопированных НК ZnO путем выхода за рамки приближения невзаимодействующих одночастичных частиц [21, 27]. Он основан на самосогласованной многочастичной квантово-механической трактовке электронов проводимости в рамках приближения случайных фаз (RPA) с локальным обменом [28]. Было показано, что свободные носители заряда в полупроводниковых наночастицах образуют атомоподобные оболочки [29, 30]. Мы решаем уравнения Кона-Шэма приближения локальной плотности (LDA) для описания структуры электронной оболочки. Электронные корреляции, ответственные за коллективные плазмонные возбуждения, учитываются в RPA. Показано, что плазмонный резонанс в НК ZnO существенно отличается от хорошо известного резонанса Ми в металлических каплях. В отличие от объемных легированных НК, в поверхностноподобных легированных НК ZnO не происходит восстановления положительного заряда. Следовательно, кулоновское отталкивание между свободными электронами подталкивает их ближе к поверхности НК. В свою очередь, эта конкретная электронная конфигурация приводит к дипольной моде, в которой возбуждаются только угловые степени свободы, а радиальное движение электронов не участвует. В отличие от обычного поверхностного дипольного плазмона Ми, где электроны совершают чисто поступательные колебания, электроны в сильно легированных НК ZnO испытывают тангенциальные колебания внутри довольно тонкой электронной оболочки аналогично плазмонным колебаниям в молекулах фуллерена [31]. Мы также показываем, что переход этой плазмонной моды из классического режима в режим квантового ограничения определяется отношением размера НК к эффективному боровскому радиусу и не зависит от числа свободных электронов. Квантовые эффекты в плазмонных колебаниях приводят к синему сдвигу частоты дипольного резонанса, что хорошо согласуется с экспериментально наблюдаемой зависимостью LSPR от размера [21].

Методы

Целью исследования является теоретический анализ оптических свойств фотолегированных нанокристаллов ZnO. Конфигурации основного состояния систем с различным числом частиц рассчитывались в приближении локальной плотности. Волновые функции основного состояния представляют собой одночастичные энергии, которые были получены путем самосогласованного численного решения системы уравнений Кона-Шэма [32]. Полный базис одночастичных состояний был создан с использованием метода B-сплайнов [33] путем разложения базисных функций в полости большого радиуса на конечное число B-сплайнов. Радиус полости выбирался равным радиусу NC. Желаемая точность вычислений с использованием дискретного базиса B-сплайнов была достигнута соответствующим выбором количества и порядка используемых в вычислении B-сплайнов. Мы использовали 50 B-шлицев 7-го порядка для достижения достаточной точности (10 ⁻⁵ ) результатов. Стандартная подпрограмма RG из пакета подпрограмм eigensystem (EISPACK) была использована для получения собственных значений и собственных векторов матричного уравнения RPA [28], решение которого предоставляет нам набор энергий возбуждения диполей и соответствующие силы осцилляторов. Спектр фотопоглощения был получен путем уширения рассчитанного распределения силы колебаний лоренцевыми профилями с фиксированной шириной складки.

Результаты и обсуждение

Основная структура состояния

Мы рассматриваем систему N электроны зоны проводимости, локализованные внутри НК ZnO радиуса R . Следуя [21], мы предполагаем, что количество электронов зависит от размера НК как N =4 π нет _e R ³ / 3, где фиксированная средняя концентрация электронов, n _e =1,4 × 10 ²⁰ см ⁻³ , определяется наивысшим достижимым уровнем в процессе фотодопирования. Радиус рассматриваемых НК составляет от 2,4 до 6 нм; соответственно, количество электронов проводимости, N , варьируются от 8 до 128.

Мы используем приближение огибающей функции для описания движения электрона в предположении, что R намного больше постоянной решетки. Известно, что электронная зонная структура объемного ZnO ​​характеризуется неизотропным и непараболическим энергетическим спектром [34]. Однако для текущей проблемы коллективной динамики N делокализованных электронов, мы пренебрежем этими эффектами малого энергетического спектра и рассмотрим изотропную параболическую дисперсию энергии с эффективной массой \ (m_ {e} ^ {*} =0.3 ~ m_ {e} \) [34]. По той же причине мы рассматриваем НК ZnO как сферические системы.

Поскольку электроны сильно локализованы в объеме НК ZnO из-за сильного смещения зоны проводимости на границе НК [6], мы заставляем все волновые функции электронов обращаться в нуль на границе НК r = R . Таким образом, мы рассматриваем N взаимодействующие электроны локализованы в бесконечной сферической яме, общая нейтральность заряда которой обеспечивается положительным поверхностным распределением заряда, которое не создает никакого поля внутри НК. Эффективный гамильтониан рассматриваемой системы просто:

где V ( г _а , г _б ) обозначает парное кулоновское взаимодействие электронов. Его явное выражение, учитывающее поляризацию материала ZnO и окружающей среды, записывается как мультипольное разложение [3],

где r _< и r _> являются наименьшим и наибольшим из двух радиальных положений соответственно. Диэлектрической проницаемости ZnO и толуола присваиваются их объемные значения ε _я =3,7 и ε _м =2.25 [21] соответственно. С этими параметрами эффективный радиус Бора \ (a_ {0} =\ hbar ^ {2} \ varepsilon _ {i} / m_ {e} ^ {*} e ^ {2} =0,65 \) нм меньше, чем Радиус ЧПУ.

Энергии одночастичных электронов, ε _я , и огибающие волновые функции ψ _я удовлетворяют системе LDA-уравнений Кона-Шэма,

где средний потенциал поля V _мф дается суммой прямых, V _Д ( г ) и обменять, V _x ( г ), детали,

где \ (\ rho =\ sum _ {i} | \ psi _ {i} | ^ {2} \) - плотность электронов. Обратите внимание, что мы могли бы заменить член обмена, зависящий от локальной плотности, в его дираковской форме на более реалистичный член обменной корреляции, зависящий от локальной плотности, как это обычно делается. Мы не делаем этого, так как теоретическое построение возбужденных состояний, которое будет следовать автоматически, учитывает большую часть корреляций основных состояний, присущих природе RPA.

Для простоты мы рассматриваем сферически-симметричные электронные конфигурации с замкнутыми электронными оболочками. В этом случае одночастичные волновые функции задаются как произведения радиальной, угловой и спиновой составляющих [35]. Следовательно, индекс i =( n , l ), где n - радиальное квантовое число, а l угловой момент. Численное решение уравнения. (3) для числа электронов N <130 показали, что основная электронная конфигурация состоит из занятых электронных состояний с наименьшими радиальными квантовыми числами n =1. Эти электронные состояния имеют безузловые радиальные волновые функции и различаются значениями угловых моментов l . Таким образом, с учетом спинового вырождения «магические» числа электронов для таких симметричных конфигураций равны N =2 ( l _макс +1) ² , где l _макс - максимальный момент количества движения наивысшего занятого электронного состояния. На рис. 1 показаны распределения плотности ρ ( г ) для ЧПУ с N =18, 50, 128 электронов. Видно, что радиальное распределение плотности становится все более узким и смещается в сторону границы раздела NC с увеличением размера. На вставке к рис. 1 показана размерная зависимость среднего электронного значения электронного радиального распределения 〈 r 〉 От радиуса NC R и отношение δ г / R , его дисперсии \ (\ delta r =\ sqrt {\ langle r ^ {2} \ rangle - {\ langle r \ rangle} ^ {2}} \) (которую можно рассматривать как эффективную ширину электронной оболочки) до радиус NC. Это соотношение составляет всего ∼ 0,15 для наименьшего НК с N . =8 электронов быстро убывает для больших систем. Численно ширина электронной оболочки δ г составляет примерно две трети эффективного радиуса Бора a ₀ тогда как пик электронной оболочки смещен от границы раздела NC из-за квантового отражения примерно на R - 〈 r 〉 ≃2 a ₀ . Эта особенность электронной системы следует из сильного кулоновского отталкивания, которое толкает электроны к границе NC, образуя полое сферическое распределение заряда. Если радиус NC достаточно велик, сила кулоновского отталкивания на границе NC e ² N / ε _я R ² становится намного сильнее центробежной силы \ (\ hbar ^ {2} l (l + 1) / m_ {e} ^ {*} {\ langle r \ rangle} ^ {3} \) даже для самого высокого занятого состояния с \ (l =l_ {max} =\ sqrt {N / 2} -1 \). Видно, что их соотношение составляет a ₀ / 2 R . Вот почему радиальное и угловое движения электронов разделены, если R ≫ а ₀ . В этом случае электронная система подобна квантовому ротатору, например, энергетический спектр занятых одночастичных состояний ε _я уравнения (3) хорошо аппроксимируется формулой

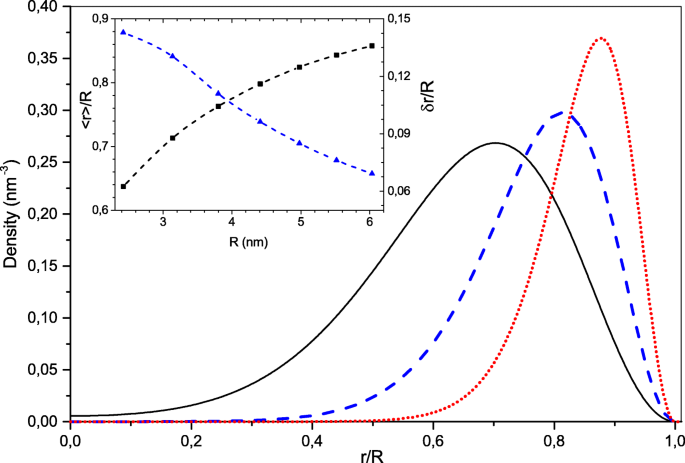
Распределения радиальной плотности для НК с разным числом делокализованных электронов, N =18 (сплошная черная линия), 50 (пунктирная синяя линия), 128 (пунктирная красная линия). На вставке приведенный средний радиус (черный) и его дисперсия (синий) представлены как функция от радиуса NC

Оптический ответ

В приближении линейного отклика внешнее гармоническое электрическое поле индуцирует зависящие от времени самосогласованные поля той же частоты. Знание соответствующих колебаний малой амплитуды дает информацию о возбужденных состояниях диполя, а также о вероятностях переходов между основным состоянием и возбужденными состояниями. Для системы, основное состояние которой является определителем Слейтера | Φ ₀ >, коррелированные многочастичные дипольные возбужденные состояния в рамках подхода RPA строятся как линейная суперпозиция возбуждения частица-дырка [36]:

. $$ (6)

Индексы i , м , ( j , n ) относятся к одночастичным состояниям выше (ниже) уровня Ферми F; \ (\ hat {a} ^ {+} \) и \ (\ hat {a} \) - одночастичные операторы создания и уничтожения, соответственно.

Прямые амплитуды \ (X_ {ij} ^ {\ nu} \) и обратные \ (Y_ {ij} ^ {\ nu} \) могут быть получены путем решения матричного уравнения RPA [ 28]:

$$ \ left (\ begin {array} {ll} \ mathbf {A} &\ mathbf {B} \\ \ mathbf {B} ^ {\ star} &\ mathbf {A} ^ {\ star} \ end { массив} \ right) \ left (\ begin {array} {l} \ mathbf {X} ^ {\ nu} \\ \ mathbf {Y} ^ {\ nu} \ end {array} \ right) =\ omega_ { \ nu} \ left (\ begin {array} {l} \ mathbf {X} ^ {\ nu} \\ - \ mathbf {Y} ^ {\ nu} \ end {array} \ right), $$ (7 )

где собственные значения ω _ν - энергии возбуждения. Матрицы A и B определены следующим образом

$$ {\ begin {align} A_ {ij, mn} &\, =\, \ delta_ {im} \ delta_ {jn} \ left (\ varepsilon_ {i} - \ varepsilon_ {j} \ right) \, + \, \ left \ langle в \ left | \ hat {v} \ right | jm \ right \ rangle, \ quad B_ {ij, mn} &\, =\, \ left \ langle im \ left | \ hat {v} \ right | jn \ right \ rangle \\ \ hat {v} (\ mathbf {r}, \ mathbf {r} ^ {\ prime}) &=V (\ mathbf {r}, \ mathbf {r} ^ {\ prime} ) + \ delta \ left (\ mathbf {r} - \ mathbf {r} ^ {\ prime} \ right) \ delta V_ {x} / \ delta \ rho. \ конец {выровнено}} $$ (8)

Попутно отметим, что обратные амплитуды \ (Y_ {ij} ^ {\ nu} \) измеряют вклад корреляций электрон-дырка в основное состояние \ (\ hat {a} _ {j} ^ {+} \ hat { a} _ {i} | \ Phi _ {0}> \) соответственно возбуждению возбужденного состояния | Φ _ν > частоты ω _ν .

Соответствующие силы дипольного осциллятора f _ν выражаются через амплитуды RPA X ^ν и Д ^ν ,

$$ f _ {\ nu} =\ frac {2 m_ {e} ^ {*} D ^ {2} _ {\ nu} \ omega _ {\ nu}} {\ hbar ^ {2}}, \ quad D_ { \ nu} =\ sum_ {ij} \ left (X ^ {(\ nu)} _ {ij} d_ {ij} + Y ^ {(\ nu)} _ {ij} d_ {ji} \ right), $ $ (9)

где d _ij =〈 я | z | j 〉 - одночастичные дипольные матричные элементы.

Сечения фотопоглощения были получены путем расширения рассчитанного распределения силы осцилляторов лоренцевыми профилями с шириной складки 0,2 ω . Спектры фотопоглощения вместе с распределениями силы осцилляторов для НК с N =8 (а), 32 (б), 50 (в) и 128 (г) электронов показаны на рис. 2. На рис. 2г мы сравниваем рассчитанное сечение фотопоглощения с экспериментальными данными [5]. [21] для ZnO NC с R ≃ 6 нм. Видно, что во всех рассмотренных НК в спектрах преобладает одна резонансная линия, положение которой фактически определяет максимум сечения фотопоглощения. Действительно, этого следовало ожидать, поскольку одночастичный электронный спектр похож на квантовый ротатор. Наиболее сильные переходы происходят при максимальном перекрытии волновых функций, т.е. при одинаковом радиальном квантовом числе n . В нашем случае есть только один такой оптический переход из наивысшего занятого состояния j =(1, l _макс ) в самое низкое вакантное состояние i =(1, l _макс +1). Однако соответствующее дипольное возбуждение сильно отличается от невзаимодействующего одночастичного перехода, когда сильное кулоновское отталкивание делает корреляции электронов важными и подавляющими. Это тот случай, когда R ≫ а ₀ . А именно энергия коллективного возбуждения ω _ν , превышает энергию одночастичного перехода

$$ \ Delta =\ left (\ epsilon_ {1, l_ {max} +1} - \ epsilon_ {1, l_ {max}} \ right) =\ frac {\ hbar ^ {2} (l_ {max} + 1)} {m_ {e} ^ {*} {\ langle r \ rangle} ^ {2}}. $$ (10)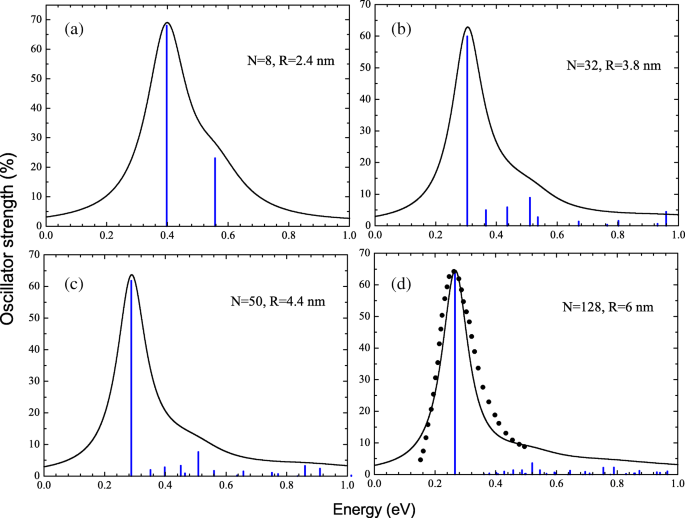

Распределения силы осцилляторов и соответствующие профили пиков фотопоглощения, рассчитанные в рамках подхода RPAE для NC с N =8 ( а ), 32 ( б ), 50 ( c ) и 128 ( d ) электроны зоны проводимости. Сравнение экспериментальных [21] (черные квадраты) и расчетных (сплошная линия) профилей резонансных пиков для NC с R ≈6 нм ( d )

На рис. 3 мы сравниваем положения максимумов фотопоглощения ω _res , рассчитанные здесь (синие кружки) с экспериментальными результатами [21] (красные звезды). Наблюдается замечательное согласие между экспериментальными данными и нашими теоретическими результатами. Для сравнения мы также наносим сюда энергии Δ одночастичного перехода (зеленые квадраты). Электронные корреляции значительно увеличивают энергию коллективного возбуждения по сравнению с Δ . Простой анализ RPA Eq. (7) объясняет это наблюдение. Если рассматривать только основной оптический переход от j =(1, l _макс ) на j =(1, l _макс +1) утверждает, что уравнение RPA. (7) сводится к матричному уравнению 2 × 2, у которого собственное значение ω просто:

$$ \ omega ^ {2} =\ Delta ^ {2} + 2V \ Delta, $$ (11)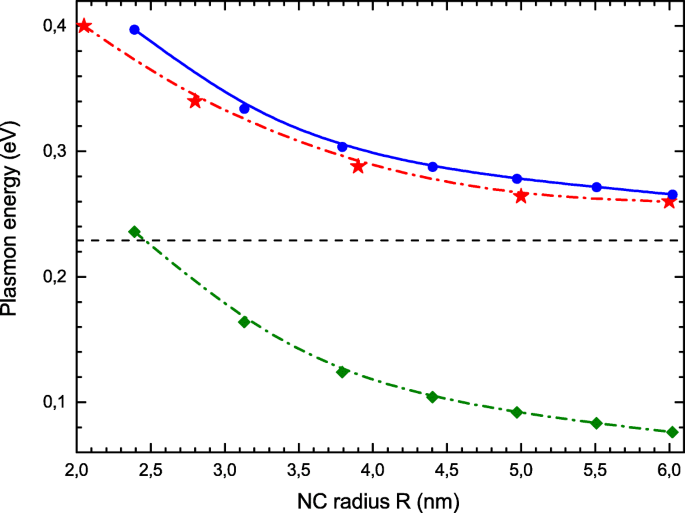

Размерная зависимость энергии LSPR. Экспериментальные значения [21] (красные звезды), RPA с локальным обменом (синие кружки), энергии одночастичного перехода (зеленые ромбы на нижней кривой). Классическое значение (13) показано горизонтальной пунктирной линией

где \ (V =\ left \ langle ij \ left | \ hat {v} \ right | ij \ right \ rangle \) обозначает кулоновский матричный элемент RPA. Первый член в прав. уравнения (11) дает одночастичный вклад, тогда как второй член является результатом взаимодействия частиц с дырками. Их соотношение можно оценить, взяв радиальную координату электрона на поверхности r = R в матричном элементе RPA V , и пренебрегая сроком обмена. Эта оценка дает

$$ \ frac {2V} {\ Delta} \ simeq \ frac {4R \ varepsilon_ {i}} {a_ {0} (\ varepsilon_ {i} +2 \ varepsilon_ {m})} \ simeq \ frac {2R} {а_ {0}}. $$ (12)

Таким образом, вклад электронных корреляций доминирует, если R ≫ а ₀ . В пределе больших НК распределение электронной плотности сосредоточено на поверхности НК; поэтому, согласно формуле. (12) резонансная энергия в уравнении. (11) имеет тенденцию

$$ \ omega =\ sqrt {\ frac {2 \ hbar ^ {2} e ^ {2} N} {m_ {e} ^ {*} (\ varepsilon_ {i} +2 \ varepsilon_ {m}) R ^ {3}}}, $$ (13)

что в точности совпадает с частотой классического дипольного плазмона в тонкой сферической оболочке [37]. Эта плазмонная мода соответствует тангенциальному колебанию электрона. Таким образом, он похож на резонанс поверхностного плазмона в C ₆₀ молекулы, где резонансная частота хорошо описывается уравнением, аналогичным уравнению. (13) [38]. Отметим, что, как и в случае фуллерена [39], эта плазмонная мода собирает две трети общей силы колебаний (см. Рис. 2). Это происходит потому, что это колебание включает только угловые степени свободы, сохраняя невозмущенное радиальное движение.

В отличие от хорошо известной дипольной поверхностной плазмонной моды в однородных сферах, которая носит чисто поступательный характер, рассматриваемый здесь режим является компрессионным. Индуцированная плотность создает электрическое поле, параллельное поверхности, которое играет роль восстанавливающей силы для этой плазмонной моды. Более того, чисто квантовое изменение локального уровня Ферми из-за индуцированных осцилляций плотности вносит вклад в восстанавливающую силу. Соответствующий квантовый вклад давления в резонансную частоту определяется выражением Δ член в формуле. (11). Он меньше кулоновского вклада во всех рассмотренных НК из-за малости эффективного боровского радиуса a ₀ в ZnO. Однако в NC с большим значением a ₀ , можно было наблюдать переход от классического дипольного плазмонного резонанса к режиму размерного квантования при R ∼ а ₀ . Стоит отметить, что в случае легированных НК параметр a ₀ / R который контролирует классический / квантовый характер дипольного резонанса, зависит только от размера NC и не зависит от количества свободных носителей N .

На рис. 3 горизонтальная линия соответствует энергии классического плазмонного резонанса (13). Голубой сдвиг резонансной частоты по сравнению с ее классическим значением вызван двумя квантовыми эффектами:квантовым вкладом давления, о котором говорилось выше, и уменьшением среднего радиуса электрона. Последнее происходит из-за того, что электроны выталкиваются в объем NC из-за квантового отражения от границы, так что 〈 r 〉 ≃ R −2 а ₀ . Этот эффект увеличивает матричный элемент V что, в свою очередь, увеличивает резонансную частоту. Примерно этот эффект можно воспроизвести, заменив ЧПУ радиус R в знаменателе уравнения. (13) автор:〈 r 〉. Согласно уравнениям. (11) - (13), оба эффекта обеспечивают сдвиг частоты синего цвета, пропорциональный обратному радиусу NC ∝1 / R . Однако в количественном отношении вклад последнего является наибольшим.

Выводы

В заключение этого письма мы разработали теорию, которая хорошо предсказывает сильный дипольный резонанс, наблюдаемый в сильно легированных n-примесью коллоидных НК ZnO. Новый тип поверхностных дипольных плазмонных возбуждений теоретически исследован с использованием многочастичного квантового подхода. Мы продемонстрировали, что сильное кулоновское отталкивание в фотодопированных нанокристаллах ZnO приводит к специфическому распределению электронов в основном состоянии, локализованному в тонком поверхностном слое вблизи внутренней поверхности. Когда диполь возбужден, это электронное распределение поддерживает коллективные плазмонные колебания, которые по существу формируются из углового движения. Переход этой поверхностной плазмонной моды из классического режима в режим квантового ограничения определяется одним параметром, равным отношению размера нанокристалла к эффективному боровскому радиусу. Отражение электронов от границы раздела NC уменьшает радиус электронной оболочки. Кроме того, изменение локального уровня Ферми дает дополнительный вклад в восстанавливающую силу плазмонного осциллятора. Эти квантовые эффекты приводят к размерной зависимости частоты резонансных плазмонов, что замечательно согласуется с экспериментальными наблюдениями. В пределе большого радиуса НК резонансная линия плавно стремится к классической плазмонной частоте заряженной оболочки бесконечно малой ширины.

Сокращения

LDA:

Приближение локальной плотности

LSPR:

Локализованный поверхностный плазмонный резонанс

NC:

Нанокристалл

RPA:

Аппроксимация случайной фазы