Теорема подстановки - пошаговое руководство с решенным примером
Анализ и решение электрических цепей с использованием теоремы подстановки
Теорема о подстановке
Как следует из названия, теорема подстановки используется для замены одного элемента схемы другим элементом. Но при замене элемента нужно иметь в виду, что поведение схемы не должно измениться.
Теорема о замещении утверждает, что
Эта теорема используется для доказательства нескольких теорем. Чтобы заменить ветвь сети, эта теорема сообщает нам граничные условия.
Если значение тока проходит через ветвь и известно значение напряжения на ветви, мы можем заменить эту ветвь другими элементами, такими как источник напряжения, источник тока, различные значения резисторов и т. д. при этом исходное состояние остается неизменным.
Эта теорема неприменима, когда цепь имеет более двух источников, соединенных последовательно или параллельно.
- Публикация по теме:Теорема Тевенина. Пошаговое руководство с примером решения
Объяснение теоремы подстановки
Теорема подстановки — это замена любой ветви сети эквивалентной ветвью, состоящей из других элементов. В этой теореме, если какая-либо ветвь или элемент заменены источником напряжения и тока, который совпадает с исходной сетью, имеет напряжение и ток этой ветви.
Давайте разберемся в теореме подстановки с сетью, показанной на рисунке ниже.
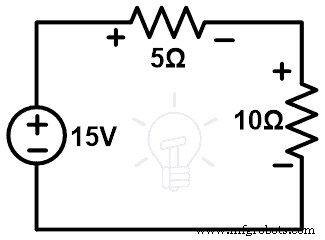
Как показано на рисунке выше, он имеет два резистора, соединенных последовательно с источником постоянного тока. Теперь мы попробуем заменить любую ветвь или элемент другими элементами. Перед этим нам нужно знать напряжение и ток, которые проходят по всем ветвям.
Здесь эта схема имеет только один цикл. Поэтому ток проходит по всем ветвям и элементам одинаков. Этот ток можно определить, подав КВЛ в сеть.
Допустим, I количество тока, проходящего через контур.
+15 =5I + 10Я
15 =15I
Я =1А
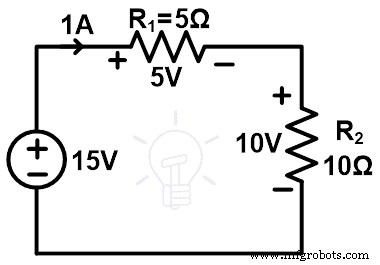
Итак, ток, проходящий через каждый элемент, равен 1 А. Теперь нам нужно найти напряжение на всех элементах.
Одна ветвь имеет источник напряжения. Итак, мы не находим напряжение той ветки. Это напряжение делится на два резистора. И нам нужно найти напряжение на каждом резисторе. Его можно найти, применив правило делителя напряжения.
Итак, напряжение на резисторе 5 Ом равно;
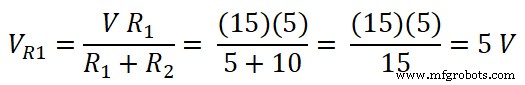
Аналогично, напряжение на резисторе 10 Ом равно;
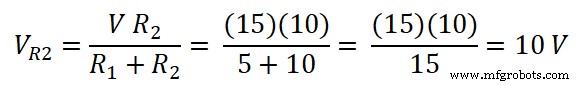
- Публикация по теме:Теорема Нортона. Пошаговое руководство с примером решения
Заменить-1
Мы можем заменить ветвь резистора 10 Ом на источник напряжения 10 В, как показано на рисунке ниже.
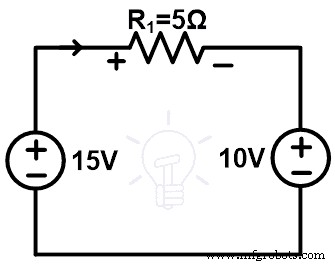
Теперь примените KVL к сети,
+15–10 =5I
5 =5I
Я =1А
Таким образом, ток контура такой же, как и в исходной цепи. Теперь вычислите напряжение на элементах. Ветвь резистора 10 Ом заменена источником 10 В. Следовательно, напряжение на этой ветви равно 10 В. И это напряжение совпадает с напряжением этой ветви в исходной цепи.
Теперь найдите напряжение на ветви резистора 5 Ом. Через эту ветвь проходит ток 1А. Следовательно, согласно закону Ома;
V 5 Ом =1А × 5 =5В
Итак, ток проходит через все ответвления, а напряжение во всех ответвлениях такое же, как и в исходной сети.
Заменить-2
Удалите ветку резистора 5 Ом. И замените эту ветвь источником напряжения 5В. Принципиальная схема этой замены показана на рисунке ниже.
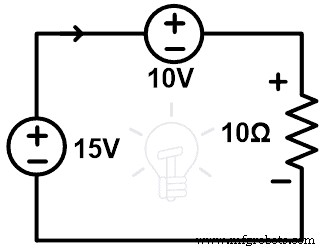
Теперь рассчитайте ток и напряжение всех ветвей и сравните их с исходной сетью.
Чтобы найти ток, проходящий через цикл, примените KVL;
+15–5 =10I
10 =10I
Я =1А
Поэтому контурный ток или ток, проходящий через элементы, совпадает с током, проходящим через исходную сеть.
Ветвь резистора 5 Ом заменена источником напряжения 5 В. Следовательно, напряжение этой ветви такое же, как и напряжение в исходной сети. Теперь нам нужно рассчитать напряжение на ветви резистора 10 Ом.
Ток, проходящий через ветвь резистора 10 Ом, составляет 1 А. По закону Ома;
V 10 Ом =ИК
V 10 Ом =1 × 10
V 10 Ом =+10 В
Итак, после замены резистора 5 Ом на источник напряжения 5 В поведение сети не изменилось.
- Публикация по теме: Теорема о суперпозиции — анализ цепей с решенным примером
Заменить-3
Удалите ветвь резистора 10 Ом и замените ее источником тока 1 А. Принципиальная схема после замены показана на рисунке ниже.
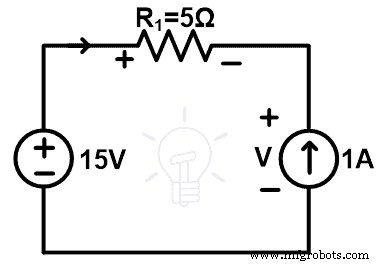
В цепи есть источник тока. Поэтому ток, проходящий через петлю, такой же, как и величина тока источника. В этом состоянии к сети подключен источник тока 1А. Следовательно, ток, проходящий через петлю, равен 1 А, что соответствует току, проходящему через исходную сеть.
Теперь рассчитайте напряжение на резисторе 5 Ом и источнике тока 1 А.
В соответствии с законом Ома,
V 5 Ом =ИК
V 5 Ом =1 × 5
V 5 Ом =+5 В
Теперь найдите напряжение на источнике тока 1 А. Предположим, что напряжение на источнике тока 1 А равно В.
На рисунке выше;
+15 – 5 – В =0
V =+10 В
Итак, доказано, что напряжение и ток, проходящий через все элементы, такие же, как и в исходной сети после замены резистора 10 Ом на источник тока 1 А.
- Публикация по теме:Теорема Миллмана. Анализ цепей переменного и постоянного тока. Примеры
Подстановка-4
Удалите ветвь резистора 10 Ом и замените ее резистором 5 Ом, подключенным последовательно к источнику напряжения 5 В. Принципиальная схема этого заменителя показана на рисунке ниже.
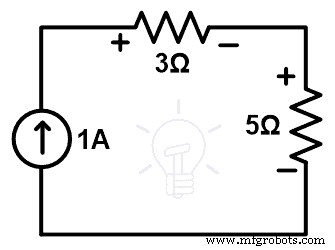
Теперь нам нужно найти текущие проходы в цикле. Итак, применим KVL к вышеуказанной сети.
15 – 5 =5I + 5Я
10 =10I
Я =1А
Итак, текущие проходы через элемент такие же, как и в исходной сети. Теперь найдите напряжение на всех элементах.
Чтобы найти напряжение на резисторе 5 Ом; мы используем закон Ома.
V 5 Ом =ИК
V 5 Ом =1 × 5
V 5 Ом =5 В
Теперь найдем напряжение в точках A и B.
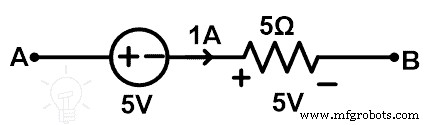
Из приведенного выше рисунка видно, что ток, проходящий через резистор 5 Ом, равен 1 А. Итак, напряжение на этом элементе равно 5В. А общее напряжение между точками A и B равно
V АВ =5 + V 5 Ом
V АВ =5 + 5
V АВ =+10В
Следовательно, после замены ветви резистора 10 Ом резистором 5 Ом и источником напряжения 5 В поведение сети остается прежним.
Итак, можно сказать, что существует несколько доступных методов поиска замены элемента любой сети без изменения напряжения и тока элемента и без изменения поведения сети. сети.
- Публикация по теме: Теорема Теллегена — Решенные примеры и моделирование MATLAB
Шаги решения сети с помощью теоремы подстановки
Шаг 1 Найдите напряжение и ток всех элементов сети. Как правило, напряжение и ток можно рассчитать, просто используя KCL, KVL или закон Ома.
Шаг 2 Найдите соответствующую ветвь, которую вы хотите удалить с помощью другого элемента, такого как источник тока, источник напряжения или сопротивление.
Шаг 3 Найдите подходящее значение заменяемого элемента при условии, что напряжение и ток не должны изменяться.
Шаг 4 Проверьте новую цепь, рассчитав напряжение и ток всех элементов. И сравните его с исходной сетью.
Это все о теореме подстановки. Теперь давайте рассмотрим пример.
- Похожая запись: Теорема о максимальной передаче мощности для цепей переменного и постоянного тока
Пример и решение теоремы о подстановке
Решите приведенную ниже схему, используя теорему подстановки, чтобы вычислить ток и напряжение на всех резисторах.
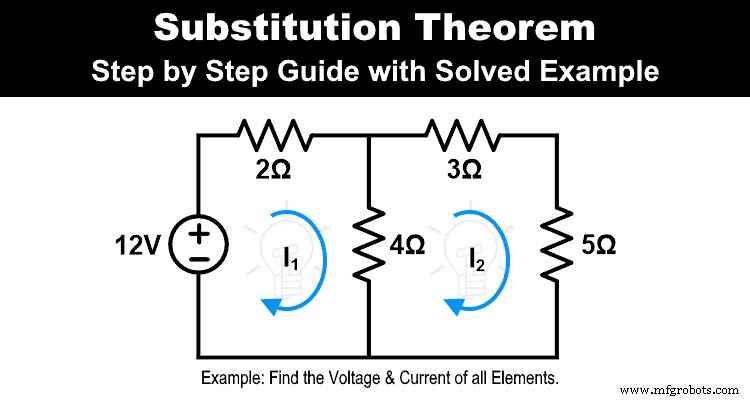
Шаг 1 Найдите напряжение и ток всех элементов. Для этого в этом примере мы применяем KVL к сети.
Применить KVL в цикле-1;
14 =6I 1 – 4Я 2 … (1)
Применить KVL в цикле-2;
0 =12I 2 – 4Я 1
12Я 2 =4Я 1
Я 1 =3Я 2 … (2)
Поместите это значение в уравнение-1;
14 =6(3I 2 ) – 4Я 2
14 =18I 2 – 4Я 2
14 =14I 2
Я 2 =1А
Из уравнения-2;
Я 1 =3А
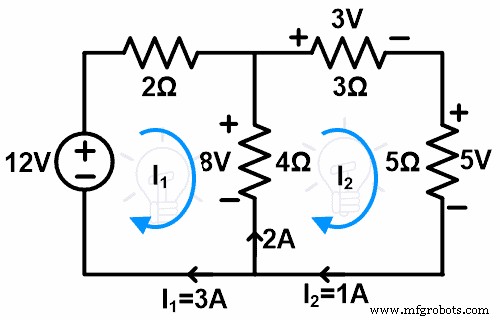
Шаг 2 Теперь мы удалим ответвления петли-1 и создадим одну петлю.
Шаг 3 Мы можем поставить источник напряжения или источник тока вместо резистора 4 Ом. Здесь мы поместим текущий источник.
Ток, проходящий через петлю-2, составляет 1 А. Поэтому заменяем ветку на источник тока 1А. Итак, оставшаяся схема показана на рисунке ниже.

Шаг 4 Давайте проверим напряжение и ток всех элементов.
Эта сеть имеет один цикл. И этот цикл имеет текущий источник. Таким образом, значение тока, проходящего через контур, такое же, как значение источника тока.
Здесь значение текущего источника равно 1A. Следовательно, ток проходит через ветвь резистора 3 Ом, а ветвь резистора 5 Ом составляет 1 А, что совпадает с исходной сетью.
Теперь найдите напряжение на резисторе 3 Ом, используя закон Ома;
V 3 Ом =ИК
V 3 Ом =1 х 3
V 3 Ом =3В
Теперь найдите напряжение на резисторе 5 Ом, используя закон Ома;
V 5 Ом =ИК
V 5 Ом =1 х 5
V 5 Ом = 5В
Итак, напряжение и ток такие же, как и в исходной сети. Так работает теорема о подстановке.
Вместо источника тока, если мы выберем источник напряжения на шаге 3. В этом состоянии значение источника напряжения аналогично значению ветви резистора 4 Ом.
В исходной сети ток проходит через ветвь резистора 4 Ом;
Я 1 – Я 2 =3 – 1 =2А
Согласно закону Ома;
V 4 Ом =2 х 4 =8В
Итак, нам нужно соединить источник напряжения 8 В с сетью, а оставшаяся схема показана на рисунке ниже.
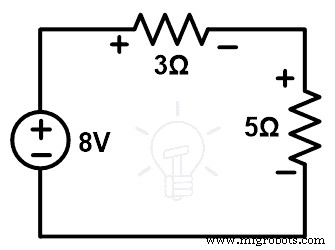
Шаг 4. Проверьте напряжение и силу тока. Примените KVL к вышеуказанному циклу.
8 =3I + 5Я
8 =8I
Я =8А
Напряжение на резисторе 3 Ом;
V 3 Ом =1 × 3 =3В
Напряжение на резисторе 5 Ом;
V 5 Ом =1 × 5 =5В
Итак, напряжение и ток после замены такие же, как и в исходной сети.
Связанные руководства по анализу электрических цепей:
- Анализ схемы СУПЕРУЗЛА — шаг за шагом с решенным примером
- Анализ цепей SUPERMESH — пошаговый пример решения
- Закон Кирхгофа о токе и напряжении (KCL и KVL) | Решенный пример
- Калькулятор правила Крамера — система уравнений 2 и 3 для электрических цепей
- Мост Уитстона — схема, работа, вывод и приложения
- Калькуляторы для электротехники и электроники
- 5000+ формул и уравнений для электротехники и электроники
Промышленные технологии
- Теорема Миллмана
- Теорема суперпозиции
- Некоторые примеры цепей переменного тока
- Изменение затрат с существующими поставщиками:руководство
- Теорема Нортона. Простая пошаговая процедура с примером
- Теорема Тевенина. Пошаговая процедура с решенным примером
- Как запрограммировать микроконтроллер PIC18 на C? Пошаговое руководство
- Теорема Теллегена — Решенные примеры и моделирование MATLAB
- Емкостный делитель напряжения:подробное руководство
- Эквивалент LM311:полное руководство



