Теорема Тевенина. Пошаговая процедура с решенным примером

Теорема Тевенина в анализе цепей постоянного тока

Французский инженер М. Л. Тевенин , совершил один из таких квантовых скачков в 1893 году. Теорема Тевенина  (также известная как Теорема Гельмгольца–Тевенина ) сам по себе не инструмент анализа, а основа очень полезного метода упрощения активных цепей и сложных сетей. Эта теорема полезна для быстрого и простого решения сложных линейных цепей и сетей, особенно электрических цепей и электронных сетей.

Теорема Тевенина можно указать ниже:

• V_TH =Напряжение Тевенина
• Р_TH =Тевенин  Сопротивление

Публикация по теме:Теорема Нортона. Простая пошаговая процедура с примером (изображения)

Этапы анализа электрической цепи с использованием теоремы Тевенина

1. Откройте нагрузочный резистор.
2. Рассчитайте/измерьте напряжение холостого хода. Это Напряжение Thevenin (V_TH ) .
3. Открытые источники тока и короткие источники напряжения.
4. Рассчитайте/измерьте сопротивление разомкнутой цепи. Это сопротивление тевенину (R_TH ) .
5. Теперь перерисуйте схему с измеренным напряжением холостого хода (V_TH ) на шаге (2) в качестве источника напряжения и измеренное сопротивление холостого хода (R_TH ) на шаге (4) в качестве последовательного сопротивления и подключите нагрузочный резистор, который мы удалили на шаге (1). Это эквивалентная схема Thevenin. этой линейной электрической сети или сложная схема которую нужно было упростить и проанализировать с помощью теоремы Тевенина . Вы сделали это.
6. Теперь найдите общий ток, протекающий через нагрузочный резистор, используя закон Ома:I_T =V_TH / (R_TH + Р_Л ).
   

Публикация по теме:Анализ схемы SUPERMESH | Шаг за шагом с решенным примером

Пример решения по теореме Тевенина:

Пример:

Найти V_TH , R_TH и ток нагрузкиI_L протекание и напряжение нагрузки на нагрузочном резисторе на рис. (1) с использованием теоремы Тевенина .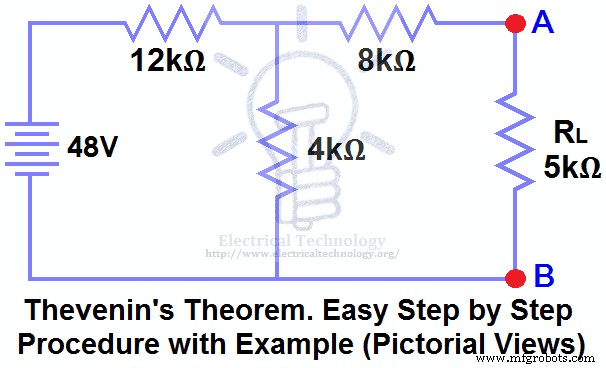

Решение:-

ШАГ 1.

Отключите нагрузочный резистор 5 кОм. (Рис. 2).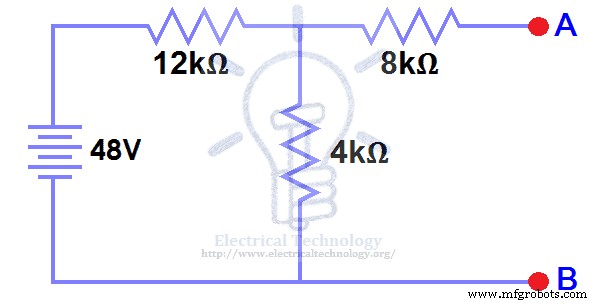

ШАГ 2.

Рассчитать/измерить напряжение холостого хода. Это Напряжение Thevenin (V_TH ) . Рис (3).

На рис. 1 мы уже убрали нагрузочный резистор, поэтому цепь стала разомкнутой. как показано на рис. 2. Теперь нам нужно рассчитать напряжение Тевенина. Поскольку 3 мА ток течет в обоих 12 кОм и 4 кОм резисторы так как это последовательная цепь, и ток не будет течь в 8 кОм резистор, поскольку он открыт.

Так, 12 В (3 мА x 4 кОм) появится через резистор 4 кОм . Мы также знаем, что ток не протекает через резистор 8 кОм, так как это разомкнутая цепь, но резистор 8 кОм подключен параллельно сопротивлению 4 кОм. . Таким образом, такое же напряжение, т. е. 12 В, появится на резисторе 8 кОм. а также резистор 4кОм. Следовательно, на клеммах AB появится 12 В. т. е.

V_TH =12 В

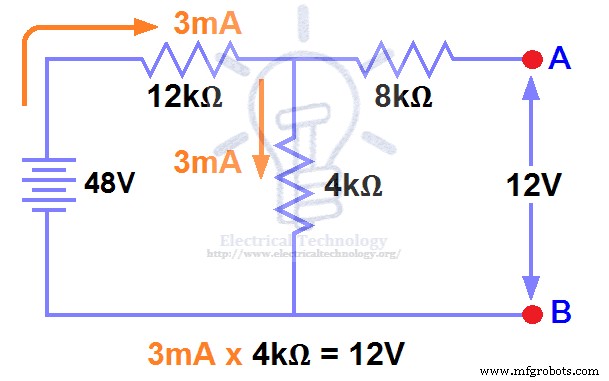
ШАГ 3.

Открыть текущие источники и источники короткого замыкания как показано ниже. Рис. (4)

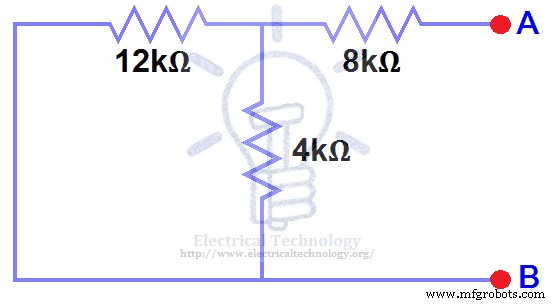
ШАГ 4.

Рассчитать / измерить сопротивление разомкнутой цепи . Это Сопротивление Тевенину (R_TH )

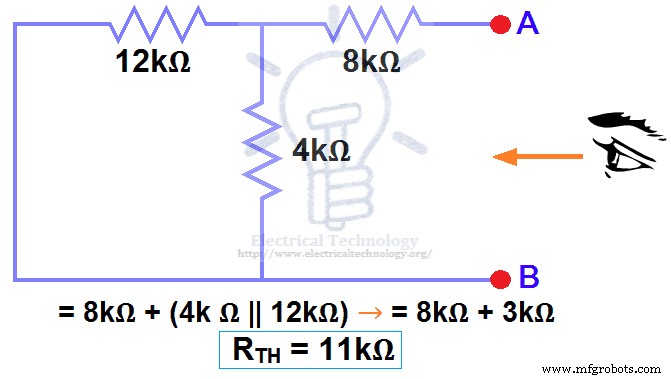
Мы удалили источник постоянного тока 48 В. до нуля как эквивалент, т. е. источник постоянного тока 48 В был заменен на короткое замыкание на шаге 3 (как показано на рис. 3). Мы видим, что резистор 8 кОм включен последовательно с параллельным соединением резистора 4 кОм и резистора 12 кОм. то есть:

8 кОм + (4 кОм || 12 кОм) ….. (|| =параллельно)

R_TH =8 кОм +  [(4 кОм x 12 кОм) / (4 кОм + 12 кОм)]

R_TH =8кОм + 3кОм

R_TH =11 кОм

ШАГ 5.

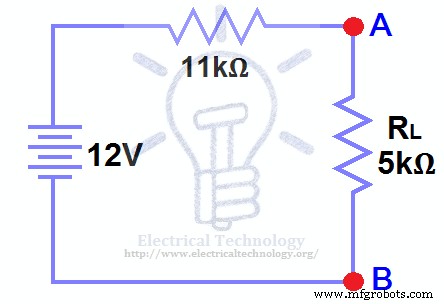
Подключите R_TH последовательно с источником напряжения V_TH и снова подключите нагрузочный резистор. Это показано на рис. (6), т. е. схема Thevenin с нагрузочным резистором. Это эквивалентная схема Тевенина .

ШАГ 6.

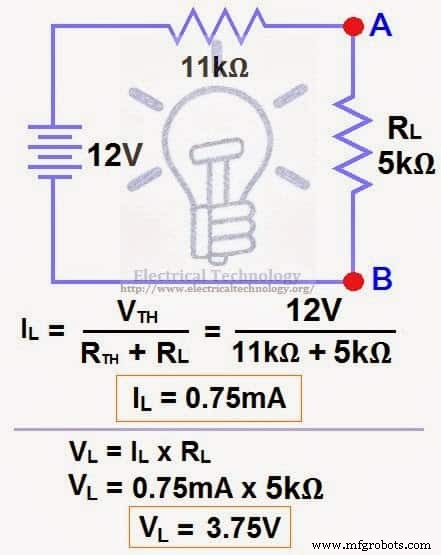
Теперь применим последний шаг, то есть закон Ома. Рассчитать общий ток нагрузки и напряжение нагрузки как показано на рис. 6.

I_L =V_TH / (R_TH + Р_Л )

I_L =12 В / (11 кОм + 5 кОм) → =12/16 кОм

I_L =0,75 мА

И

V_L =Я_Л х П_Л

V_L =0,75 мА x 5 кОм

V_L =3,75 В

Теперь сравните эту простую схему с исходной схемой, показанной на рис. 1. Вы видите, насколько проще будет измерять и вычислять ток нагрузки в сложной цепи и сети для различных нагрузочные резисторы по теореме Тевенина ? Да и только да.

Полезно знать: Теоремы Тевенина и Нортона могут быть применены к цепям переменного и постоянного тока, содержащим различные компоненты, такие как резисторы, катушки индуктивности, конденсаторы и т. д. Имейте в виду, что напряжение Тевенина «V_TH ” в цепи переменного тока выражается комплексным числом (полярная форма), тогда как сопротивление Тевенина “R_TH ” указано в прямоугольной форме.

Похожие сообщения:

• Теорема о максимальной передаче мощности для цепей переменного и постоянного тока
• Закон Кирхгофа о токе и напряжении (KCL и KVL) | Решенный пример
• Теорема о компенсации – доказательство, объяснение и примеры решения
• Теорема о подстановке — пошаговое руководство с примером решения
• Теорема Миллмана. Анализ цепей переменного и постоянного тока. Примеры.
• Теорема о суперпозиции — анализ цепей с решенным примером
• Теорема Теллегена — Решенные примеры и моделирование в MATLAB
• Анализ схемы SUPERNODE | Шаг за шагом с решенным примером
• Анализ цепей SUPERMESH | Шаг за шагом с решенным примером
• Правило делителя напряжения (VDR) — примеры решений для цепей R, L и C
• Current Divider Rule (CDR) – Решенные примеры для цепей переменного и постоянного тока
• Преобразование из звезды в дельту и из дельты в звезду. Преобразование Y-Δ