Теорема Нортона. Простая пошаговая процедура с примером

Теорема Нортона в анализе цепей постоянного тока

Теорема Нортона — еще один полезный метод анализа электрических цепей, аналогичный теореме Тевенина, которая сводит линейные, активные цепи и сложные сети к простой эквивалентной схеме. Основное различие между теоремой Тевенина и теоремой Нортона заключается в том, что теорема Тевенина обеспечивает эквивалентный источник напряжения и эквивалентное последовательное сопротивление, а теорема Нортона обеспечивает эквивалентный источник тока и эквивалентное параллельное сопротивление.

Теорема Нортона утверждает, что:

Другими, но простыми словами, любая линейная цепь эквивалентна реальному и независимому источнику тока на определенных клеммах.

Публикация по теме:Теорема Тевенина. Простая пошаговая процедура с примером (изображения)

Этапы анализа электрической цепи с использованием теоремы Нортона

1. Закоротите нагрузочный резистор.
2. Рассчитайте/измерьте ток короткого замыкания. Это Norton Current (I_N ).
3. Открытые источники тока, короткие источники напряжения и открытый нагрузочный резистор.
4. Рассчитайте/измерьте сопротивление разомкнутой цепи. Это Сопротивление Нортона (R_N ).
5. Теперь перерисуйте цепь с измеренным током короткого замыкания (I_N ) на шаге (2) в качестве источника тока и измеренное сопротивление холостого хода (R_N ) в шаге (4) в качестве параллельного сопротивления и подключите нагрузочный резистор, который мы удалили в шаге (3). Это эквивалентная схема Нортона той линейной электрической сети или сложной цепи, которую нужно было упростить и проанализировать. Вы сделали это.
6. Теперь найдите ток нагрузки, протекающий через нагрузочный резистор, и напряжение нагрузки на нагрузочном резисторе, используя правило делителя тока. Я_Л =Я_Н / (R_Н / (R_Н + Р_Л ))  ((Для ясного объяснения… проверьте приведенный ниже пример решения).

Пример решения Нортон Теорема:

Пример:

Найти R_N , я_Н , ток, протекающий через нагрузочный резистор, и напряжение нагрузки на нагрузочном резисторе на рис. (1) с использованием теоремы Нортона.

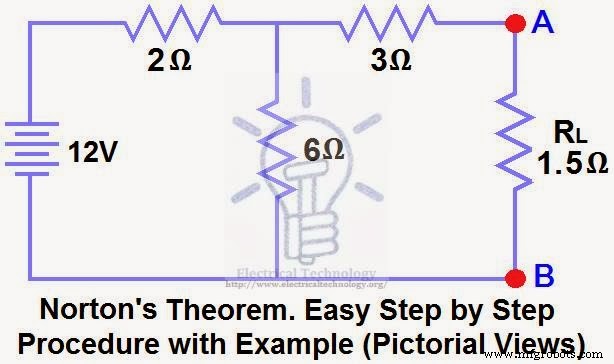
  Решение:-

ШАГ 1.

Замкните накоротко нагрузочный резистор 1,5 Ом, как показано на (рис. 2).

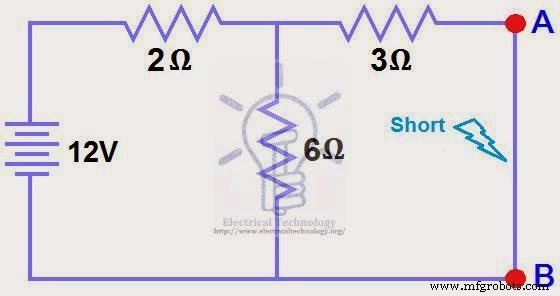
ШАГ 2.

Рассчитайте/измерьте ток короткого замыкания. Это Norton Current (I_N ).

Мы замкнули клеммы AB, чтобы определить ток Norton, I_N. Затем 6 Ом и 3 Ом соединены параллельно, и эта параллельная комбинация 6 Ом и 3 Ом последовательно соединена с 2 Ом.

Поэтому общее сопротивление цепи источнику равно:-

2 Ом + (6 Ом || 3 Ом) ….. (|| =параллельно).

R_T =2 Ом + [(3 Ом x 6 Ом) / (3 Ом + 6 Ом)] → I_T =2 Ом + 2 Ом =4 Ом.

R_T =4 Ом

Я_Т =В ÷ R_T

Я_Т =12 В ÷ 4 Ом

Я_Т =3А..

Теперь нам нужно найти I_SC =Я_Н   … Применить CDR… (Правило текущего делителя)…

Я_SC =Я_Н =3A x [(6Ω ÷ (3Ω + 6Ω)] =2A.

I_SC =I_Н =2А.

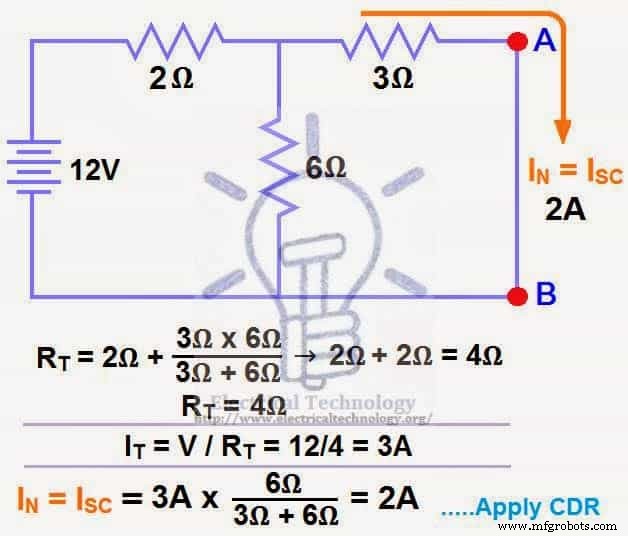
ШАГ 3.

Открытые источники тока, короткие источники напряжения и открытый нагрузочный резистор. Рис. (4)

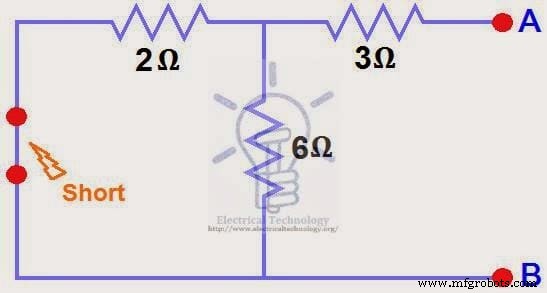
ШАГ 4.

Рассчитайте/измерьте сопротивление разомкнутой цепи. Это Сопротивление Нортона (R_N )

Мы уменьшили источник постоянного тока 12 В до нуля, что эквивалентно замене его на короткое замыкание на шаге (3), как показано на рисунке (4). Мы видим, что резистор 3 Ом последовательно с параллельной комбинацией резистора 6 Ом и резистора 2 Ом. то есть:

3 Ом + (6 Ом || 2 Ом) ….. (|| =параллельно)

R_N =3 Ом + [(6 Ом x 2 Ом) ÷ (6 Ом + 2 Ом)]

R_N =3 Ом + 1,5 Ом

R_N =4,5 Ом

<я>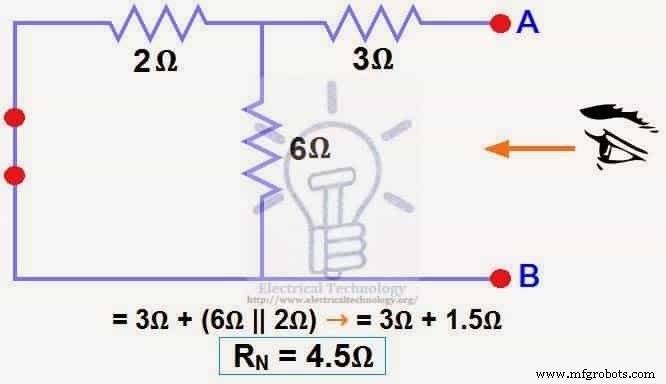

ШАГ 5.

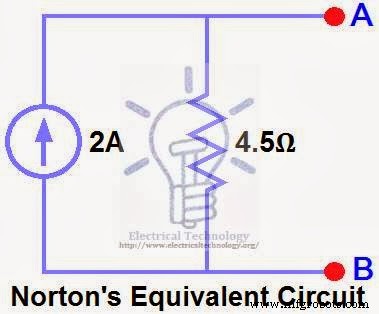
Соедините R_N параллельно с текущим источником I_N  и снова подключите нагрузочный резистор. Это показано на рис. (6), то есть эквивалентной схеме Norton с нагрузочным резистором.

ШАГ 6.

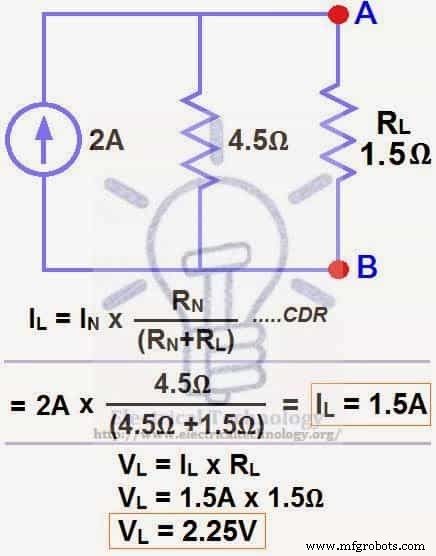
Теперь выполните последний шаг, т. е. рассчитайте ток нагрузки через нагрузочный резистор и напряжение нагрузки на нагрузочном резисторе по закону Ома, как показано на рис. 7. 

Ток нагрузки через нагрузочный резистор…

I_L =Я_Н х [R_Н ÷ (R_Н + Р_Л )]

=2 А x (4,5 Ом ÷ 4,5 Ом + 1,5 Ом) → =1,5 А

I_L =1,5 А

И

Нагрузочное напряжение на нагрузочном резисторе…

V_L =Я_Л х П_Л

V_L =1,5 А x 1,5 Ом

V_L =2,25 В

Теперь сравните эту простую схему с приведенной исходной схемой. на рисунке 1. Вы видите, насколько проще будет измерять/вычислять ток нагрузки и напряжение нагрузки для различных нагрузочных резисторов с помощью теоремы Нортона даже в гораздо более сложных схемах? Только и только да.

Полезно знать: Обе теоремы Нортона и Тевенина могут применяться как к цепям переменного, так и постоянного тока, содержащим различные компоненты, такие как резисторы, катушки индуктивности, конденсаторы и т. д. Имейте в виду, что ток Нортона «I_N ” в цепи переменного тока выражается комплексным числом (полярная форма), тогда как сопротивление Нортона “R_N ” указано в прямоугольной форме.

Похожие сообщения:

• Теорема о максимальной передаче мощности для цепей переменного и постоянного тока
• Закон Кирхгофа о токе и напряжении (KCL и KVL) | Решенный пример
• Теорема о компенсации – доказательство, объяснение и примеры решения
• Теорема о подстановке — пошаговое руководство с примером решения
• Теорема Миллмана. Анализ цепей переменного и постоянного тока. Примеры.
• Теорема о суперпозиции — анализ цепей с решенным примером
• Теорема Теллегена — Решенные примеры и моделирование в MATLAB
• Анализ схемы SUPERNODE | Шаг за шагом с решенным примером
• Анализ цепей SUPERMESH | Шаг за шагом с решенным примером
• Правило делителя напряжения (VDR) — примеры решений для цепей R, L и C
• Current Divider Rule (CDR) – Решенные примеры для цепей переменного и постоянного тока
• Преобразование из звезды в дельту и из дельты в звезду. Преобразование Y-Δ