Теорема суперпозиции

Теорема суперпозиции - это один из тех гениальных ходов, которые рассматривают сложный предмет и упрощают его до идеального смысла. Теорема, подобная теореме Миллмана, безусловно, работает хорошо, но не совсем очевидно, почему это так хорошо работает. С другой стороны, суперпозиция очевидна.

Последовательный / параллельный анализ

Стратегия, используемая в теореме суперпозиции, заключается в устранении всех источников питания в сети, кроме одного, с использованием последовательного / параллельного анализа для определения падений напряжения (и / или токов) в модифицированной сети для каждого источника питания отдельно. Затем, как только падение напряжения и / или токи были определены для каждого источника питания, работающего отдельно, все значения «накладываются» друг на друга (складываются алгебраически), чтобы найти фактические падения / токи напряжения со всеми активными источниками. Давайте еще раз посмотрим на нашу примерную схему и применим к ней теорему суперпозиции:

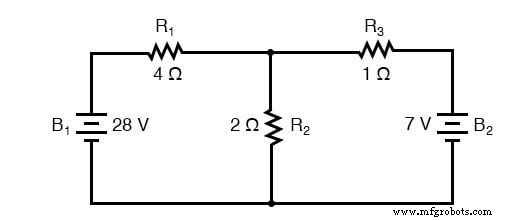
Поскольку у нас есть два источника питания в этой цепи, нам нужно будет рассчитать два набора значений для падений напряжения и / или токов, один для схемы с действующей только 28-вольтовой батареей. . .

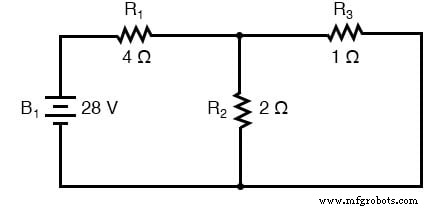
. . . и один для схемы, в которой работает только 7-вольтовая батарея:

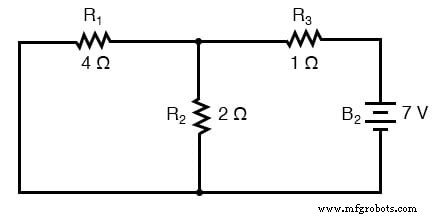
При повторном рисовании схемы для последовательного / параллельного анализа с одним источником все остальные источники напряжения заменяются проводами (короткими замыканиями), а все источники тока - с разомкнутыми цепями (обрывами). Поскольку в нашей примерной схеме есть только источники напряжения (батареи), мы заменим каждый неактивный источник во время анализа на провод.

Анализируя схему только с 28-вольтовой батареей, мы получаем следующие значения напряжения и тока:

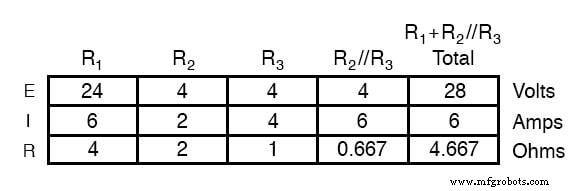
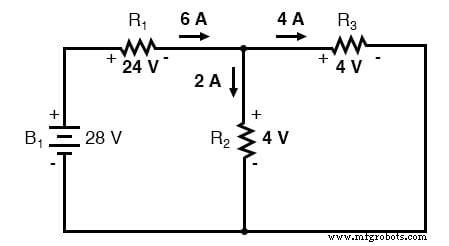
Анализируя схему только с 7-вольтовой батареей, мы получаем другой набор значений напряжения и тока:

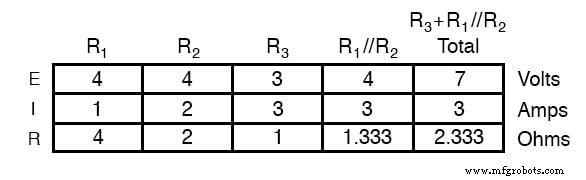
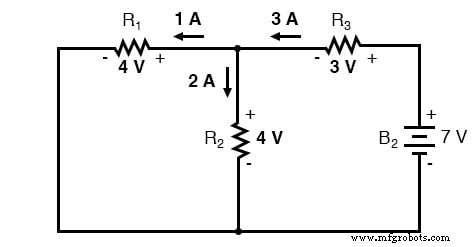
Путем наложения

При наложении этих значений напряжения и тока мы должны очень внимательно учитывать полярность (падения напряжения) и направление (потока тока), так как значения должны складываться алгебраически . .

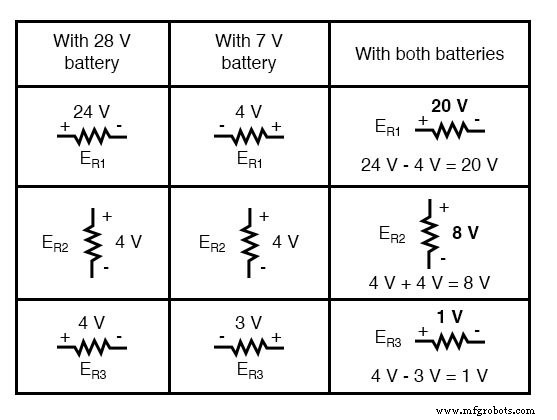
Если применить к схеме эти наложенные значения напряжения, конечный результат будет выглядеть примерно так:

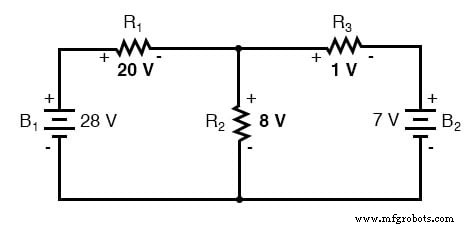
Токи также складываются алгебраически и могут либо накладываться друг на друга, как это делается при падении напряжения на резисторе, либо просто вычисляться из конечных падений напряжения и соответствующих сопротивлений (I =E / R). В любом случае ответы будут одинаковыми. Здесь я покажу метод наложения, применяемый к току:

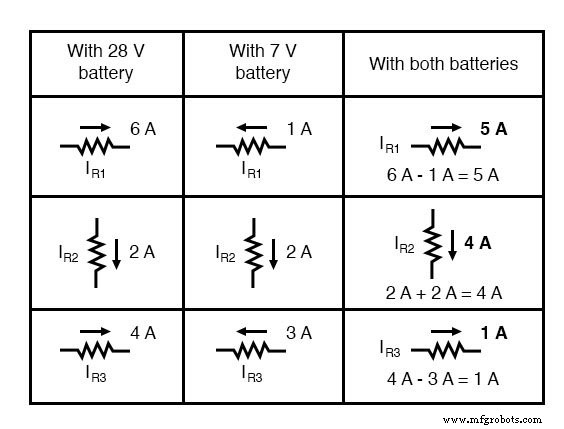
Еще раз применяем эти наложенные друг на друга фигуры к нашей схеме:

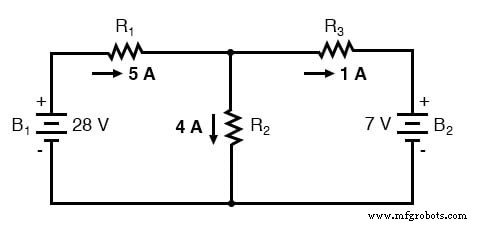
Предпосылки для теоремы суперпозиции

Довольно просто и элегантно, не правда ли? Однако следует отметить, что теорема суперпозиции работает только для схем, которые сводятся к последовательным / параллельным комбинациям для каждого из источников питания одновременно (таким образом, эта теорема бесполезна для анализа несимметричной мостовой схемы), и только работает там, где лежащие в основе уравнения линейны (без математических степеней или корней). Требование линейности означает, что теорема суперпозиции применима только для определения напряжения и тока, не мощности !!! Рассеивание мощности, являясь нелинейными функциями, алгебраически не увеличивает точную сумму, когда одновременно рассматривается только один источник. Необходимость линейности также означает, что эту теорему нельзя применять в цепях, в которых сопротивление компонента изменяется в зависимости от напряжения или тока. Следовательно, сети, содержащие такие компоненты, как лампы (лампы накаливания или газоразрядные) или варисторы, не могут быть проанализированы.

Еще одним предварительным условием для теоремы суперпозиции является то, что все компоненты должны быть «двусторонними», что означает, что они ведут себя одинаково с электронами, проходящими через них в любом направлении. Резисторы не имеют поведения, зависящего от полярности, поэтому все схемы, которые мы изучали до сих пор, соответствуют этому критерию.

Теорема суперпозиции находит применение при изучении цепей переменного тока (AC) и полупроводниковых цепей (усилителей), где иногда переменный ток часто смешивается (накладывается) с постоянным. Поскольку уравнения для переменного напряжения и тока (закон Ома) линейны, как и для постоянного тока, мы можем использовать суперпозицию для анализа схемы только с источником питания постоянного тока, а затем только с источником питания переменного тока, объединяя результаты, чтобы определить, что произойдет с переменным и переменным током. Действующие источники постоянного тока. На данный момент, однако, суперпозиции будет достаточно, чтобы избавиться от необходимости выполнять одновременные уравнения для анализа схемы.

ОБЗОР:

• Теорема суперпозиции утверждает, что схема может быть проанализирована только с одним источником питания за раз, а соответствующие напряжения и токи компонентов алгебраически сложены, чтобы выяснить, что они будут делать со всеми действующими источниками питания.
• Чтобы отключить все источники питания, кроме одного, для анализа замените любой источник напряжения (батареи) на провод; заменить любой текущий источник открытым (перерывом).

СВЯЗАННЫЙ РАБОЧИЙ ЛИСТ:

• Рабочий лист теоремы суперпозиции