Теорема о компенсации – доказательство, объяснение и примеры решения

Доказательство, объяснение, эксперимент и решенные примеры теоремы о компенсации для анализа цепей

Теорема о компенсации

В то же время в теории сетей важно знать или изучать эффект изменения импеданса в одной из ее ветвей. Это повлияет на соответствующие напряжения и токи сети или цепи. Теорема о компенсации дает информацию об изменении сети.

Теорема о компенсации работает на основе основной концепции закона Ома. Согласно закону Ома, когда через резистор проходит ток, на резисторе возникает некоторое падение напряжения. Это падение напряжения будет противодействовать напряжению источника.

Поэтому мы подключаем дополнительный источник напряжения в противоположной полярности по сравнению с напряжением источника, а величина равна падению напряжения. Теорема компенсации работает на этой концепции.

Теорема о компенсации утверждает, что

• Публикация по теме:Теорема Тевенина. Пошаговое руководство с примером решения

Объяснение теоремы о компенсации

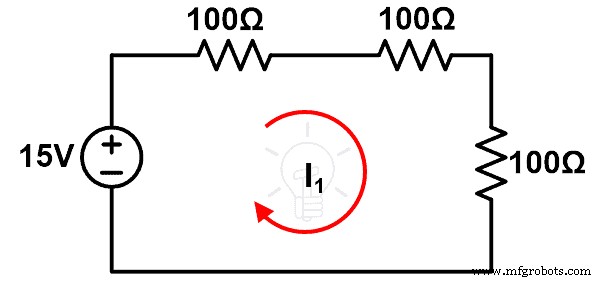
Чтобы понять теорему о компенсации, рассмотрите рисунок ниже.

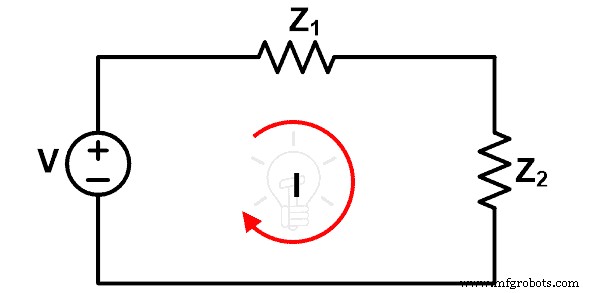
На этом рисунке источник напряжения V представляет собой независимое напряжение и источник и два импеданса Z₁ и Z₂ являются линейными или двусторонними элементами. Следовательно, к этой сети можно применить теорему о компенсации. Ток, который проходит через контур, равен I.

Теперь предположим, что импеданс Z₂ увеличилась на ∆Z. Из-за этого изменения ток, проходящий через петлю, изменяется и равен I’. Новая принципиальная схема показана на рисунке ниже.

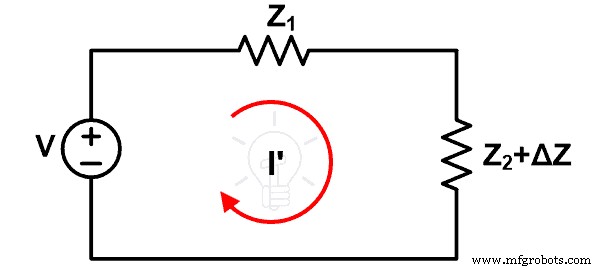
Из-за изменения импеданса изменение тока определяется ∆I.

ΔI =Я – Я

Согласно формулировке теоремы о компенсации, мы можем напрямую рассчитать изменение текущего ∆I. Для этого нам нужно изменить схему.

Первая модификация заключается в том, что подключается источник напряжения со значением I∆Z, в ветви которого изменяется импеданс. И полярность этого источника напряжения противоположна основному источнику. Недавно добавленный источник напряжения V_C называется источником компенсации.

V_C =Я ΔZ

Вторая модификация заключается в том, что нам нужно удалить старый источник напряжения по его внутреннему импедансу. Если мы рассмотрим идеальный источник напряжения, в этом состоянии мы можем удалить этот источник напряжения, замкнув накоротко его клемму. После этих изменений оставшаяся схема выглядит так, как показано на рисунке ниже.

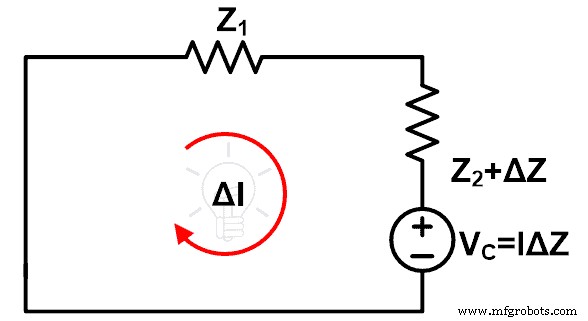
Решив приведенную выше схему, мы можем легко найти изменение тока после изменения импеданса.

• Публикация по теме:Теорема Нортона. Пошаговое руководство с примером решения

Доказательство теоремы о компенсации

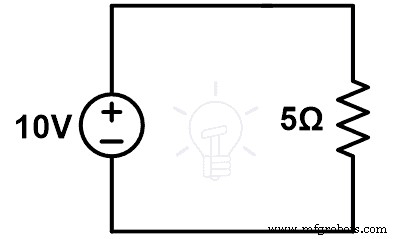
Рассмотрите схему, представленную на рисунке 1. Рассчитайте ток (I), проходящий через контур.

Применить KVL к фигуре-1;

Теперь мы предположили, что импеданс Z₂ изменяется на ∆Z. И модифицированная схема показана на рисунке 2. Нам нужно рассчитать (I’) ток, проходящий через контур на рисунке 2.

Применить KVL к фигуре-2;

Из-за изменения импеданса изменение тока контура обозначается как ∆I. А ∆I равен разнице между старым током I и новым током I’.

ΔI =Я – Я

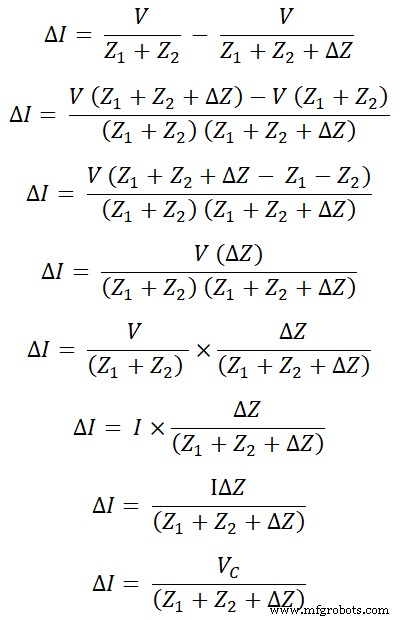
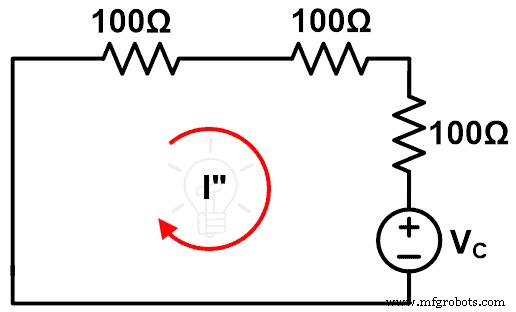
Теперь рассмотрим рисунок ниже.

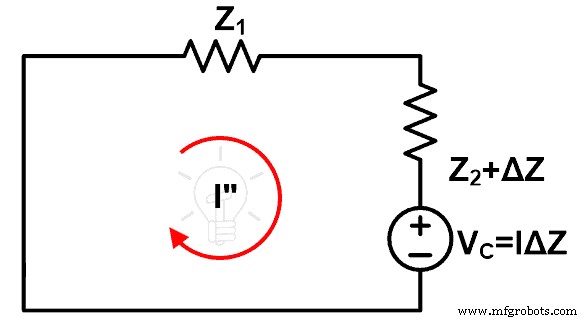
На этом рисунке показана схема после реализации теоремы о компенсации. Здесь первоначальный источник напряжения удаляется за счет короткого замыкания (предположим, что это идеальный источник напряжения).

Мы найдем текущие проходы через этот цикл, то есть I». И сравните этот ток с током, рассчитанным выше.

Чтобы рассчитать ток, проходящий через контур, примените KVL к приведенному выше рисунку.

V_C =Z ₁ Я” +(Z ₂ +ΔZ ) Я”

V_C =Я” (Я ₁ + Z ₂ + ΔZ )

Я =V_С / (Z ₁ + Z ₂ + ΔZ )

Я =ΔI

Таким образом, доказано, что изменение тока (∆I) после модификации совпадает с током, рассчитанным по теореме компенсации.

И мы доказали утверждение теоремы о компенсации.

• Публикация по теме: Теорема о суперпозиции — анализ цепей с решенным примером

Экспериментальная теорема компенсации

Цель: Докажите теорему о компенсации и найдите изменение тока.

Аппарат: Вольтметр, Амперметр, Резисторы, Соединительные провода, Макет,

Схема:

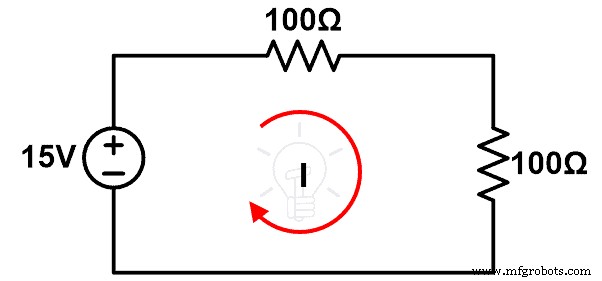
Процедура:

Шаг 1. Соедините компоненты, как показано на рис. 5, с помощью соединительного провода на макетной плате.

Шаг 2. Измерьте текущее I.

Шаг 3. Соедините компоненты, как показано на рисунке 6. Здесь мы подключили дополнительный резистор.

Шаг 4. Измерьте текущий I1.

Шаг 5. Рассчитайте изменение тока (∆I) по значениям I и I1.

Шаг 6. Соедините компоненты, как показано на рисунке 7. Эта схема является компенсационной схемой.

Шаг 7. Измерьте текущее I”.

Шаг 8. Сравните изменение тока (∆I) с I”.

Экспериментальная таблица:

<тд ширина="150"> <тд ширина="150"> <тд ширина="150"> <тд ширина="150">

Старший. Нет.	Я	Я 1	∆I	I”
1

Результат:

Сравнивая значение текущего I’’ с ∆I, мы можем доказать теорему о компенсации.

• Публикация по теме: Теорема Миллмана. Анализ цепей переменного и постоянного тока. Примеры

Пример теоремы о компенсации

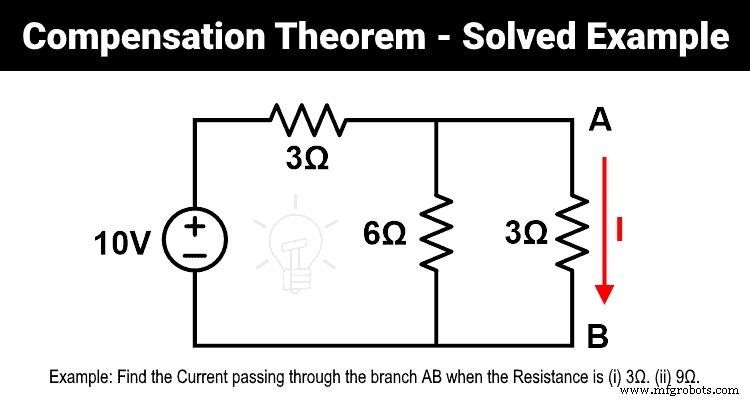
Пример 1

• 1) Найдите ток, проходящий через ветвь AB, когда сопротивление равно 3 Ом.
• 2) Найдите ток, проходящий через ветвь AB, используя теорему о компенсации, когда сопротивление 3 Ом изменяется на 9 Ом.
• 3) Докажите теорему о компенсации.

Ответ-1

Как показано на рисунке, резисторы 6 Ом и 3 Ом включены параллельно. И эта параллельная комбинация соединена последовательно с резистором 3 Ом. Следовательно, эквивалентное сопротивление будет;

R _{Уравнение} =6 | | 3+3

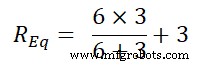
R _{Уравнение} =2 + 3

R _{Уравнение} =5 Ом

Согласно закону Ома;

10 =Я (5)

Я =10 ÷ 5

Я =2 А

Теперь нам нужно найти текущие проходы через ветвь AB. Итак, в соответствии с текущим правилом делителя;

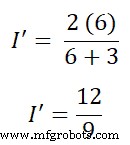
Я =1,333 А (или 3/4 А)

• Публикация по теме: Теорема о подстановке — пошаговое руководство с примером решения

Ответ 2

Нам нужно заменить резистор 3 Ом на резистор 9 Ом. Согласно теореме о компенсации нам нужно добавить новый источник напряжения последовательно с резистором 9 Ом. И значение этого источника напряжения равно;

V_C =Я ΔZ

Где

ΔZ =9 – 3 =6 Ом и I’ =4/3 А (или 1,333 А)

V_C =(4/3А) х 6 Ом

V_C =8 В

Измененная принципиальная схема или компенсированная принципиальная схема показана на рисунке ниже.

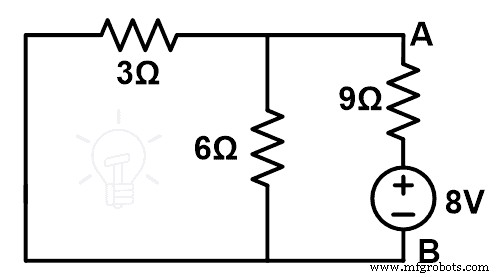
Теперь мы найдем эквивалентное сопротивление. Здесь резисторы 3 Ом и 6 Ом соединены параллельно. И эта параллельная комбинация соединена последовательно с резистором 9 Ом.

R_Eq =3 | | 6 + 9

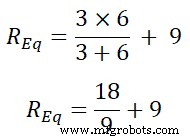
R_Eq =2 + 9

R_Eq =11 Ом

Теперь по закону Ома;

V =ΔЯ R

8 =ΔI (11 Ом)

ΔI =8 ÷ 11

ΔI =0,7272 А

Итак, согласно теореме о компенсации; изменение тока составляет 0,7272 А.

• Публикация по теме: Теорема Теллегена — Решенные примеры и моделирование MATLAB

Ответ 3

Мы хотим доказать теорему о компенсации. Итак, мы вычисляем ток в данном примере с резистором 9 Ом.

Измененная принципиальная схема показана на рисунке ниже.

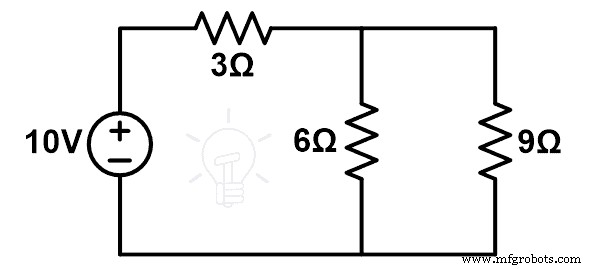
Здесь резисторы 9 Ом и 6 Ом соединены параллельно, и эта параллельная комбинация соединена последовательно с резистором 3 Ом.

Эквивалентное сопротивление равно;

R_Eq =9 | | 6 + 3

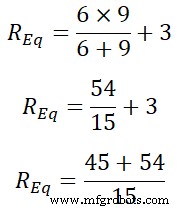
R_Eq =99 ÷ 15

R_Eq =6,66 Ом

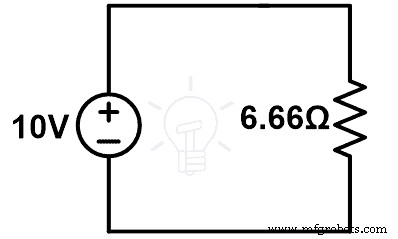
На рисунке выше;

10 =Я (6.66)

Я =10 ÷ 6,66

Я =1,5151 А

Согласно текущему правилу разделителя;

Я =0,6060 А

ΔI =Я – Я”

ΔI =(4/3А) – 0,6060

ΔI =1,333 А – 0,6060

ΔI =0,7273 А

Таким образом, доказано, что изменение тока, рассчитанное по теореме о компенсации, такое же, как изменение тока, рассчитанное по исходной схеме.

• Похожая запись:  Теорема о максимальной передаче мощности для цепей переменного и постоянного тока
  

Пример 2

В приведенной ниже схеме найдите изменение тока, если резистор 3 Ом заменить резистором 7 Ом, используя теорему о компенсации. И докажите теорему о компенсации.

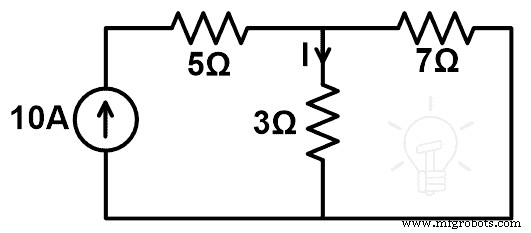
Приведенная выше сеть состоит только из резисторов и независимых источников тока. Итак, к этой сети можно применить теорему о компенсации.

На этом рисунке сеть питается от текущего источника. Теперь нам нужно найти ток, который проходит через ветвь резистора 3 Ом. Этот ток можно найти с помощью ККЛ или КВЛ. Но здесь этот ток можно легко найти по правилу делителя тока.

Поэтому в соответствии с текущим правилом разделителя;

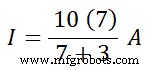
Я =70 ÷ 10 А

Я =7 А

В исходной сети с резистором 3 Ом ток, проходящий через эту ветвь, составляет 3 А. Теперь нам нужно изменить этот резистор с 3 Ом на 7 Ом. Из-за этой модификации ток, проходящий через эту ветвь, будет изменен. И это изменение тока мы найдем по теореме о компенсации.

Для этого нам нужно создать компенсационную сеть. Чтобы создать компенсационную сеть, нам нужно удалить все независимые источники, доступные в сети, замкнув накоротко источник напряжения и разомкнув источник тока.

В этой сети доступен только один текущий источник. Предположим, что источник тока является идеальным источником тока. Поэтому нам не нужно добавлять внутреннее сопротивление.

Вторая модификация, которую нам нужно внести в схему компенсации, — добавить дополнительный источник напряжения. И значение этого напряжения равно;

V_C =Я ΔZ

V_C =7 × (7 – 3)

V_C =7 × 4

V_C =28 В

Компенсационная сеть показана на рисунке ниже.

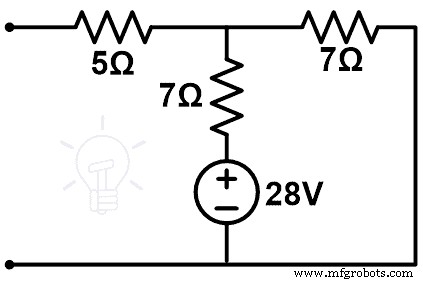
На этой фигуре только одна петля. А ток, проходящий через ветвь 7 Ом, даст нам изменение тока (∆I).

ΔI =В_С ÷ (7+7)

ΔI =28 ÷ 14

ΔI =2 А

Для доказательства теоремы о компенсации найдем ток в цепи с подключенным резистором 7 Ом. Модифицированная принципиальная схема показана на рисунке ниже.

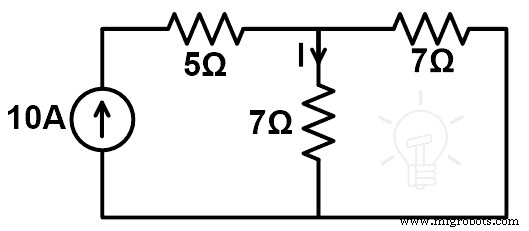
Я =(10 (7)) ÷ (7 + 7)

Я =70 ÷ 14

Я =5 А

Применяя текущее правило разделителя;

Чтобы найти изменение тока, нам нужно вычесть этот ток из тока, проходящего через исходную сеть.

ΔI =Я – Я”

ΔI =7 – 5

ΔI =2 А

Таким образом, мы доказали теорему о компенсации.

Связанные учебные пособия по анализу электрических цепей:

• Анализ схемы SUPERNODE — шаг за шагом с решенным примером
• Анализ цепей SUPERMESH — шаг за шагом с решенным примером
• Закон Кирхгофа о токе и напряжении (KCL и KVL) | Решенный пример
• Калькулятор по правилу Крамера – система из 2 и 3 уравнений для электрических цепей
• Мост Уитстона — схема, работа, происхождение и применение
• Калькуляторы для электротехники и электроники
• 5000+ формул и уравнений для электротехники и электроники