Правило делителя напряжения (VDR) – Решенные примеры для цепей R, L и C

Разделение напряжения «VDR» для резистивных, индуктивных и емкостных цепей

Что такое правило делителя напряжения?

В цепи, когда несколько элементов соединены последовательно, входное напряжение делится между элементами. А в цепи, когда несколько элементов соединены параллельно, ток делится между элементами.

Поэтому в параллельной цепи используется правило делителя тока, а в последовательной цепи правило делителя напряжения используется для анализа и решения схемы.

При последовательном соединении двух или более импедансов входное напряжение делится на все импедансы. Для расчета напряжения на каждом элементе используется правило делителя напряжения. Правило делителя напряжения — это наиболее важное и простое правило анализа цепей для расчета отдельного напряжения любых элементов.

Правило делителя напряжения также известно как правило делителя потенциала. В некоторых условиях требуется определенное выходное напряжение. Но у нас нет этой конкретной ценности источника. В этом состоянии мы делаем ряд пассивных элементов и снижаем уровень напряжения до определенного значения. И здесь правило делителя напряжения используется для расчета удельного выходного напряжения.

В соответствии с элементами, используемыми в схеме, правило делителя напряжения можно разделить на три типа; резистивный делитель напряжения, индуктивный делитель напряжения и емкостный делитель напряжения. Теперь мы докажем правило делителя напряжения для всех этих типов цепей.

Связанный пост:

• Калькулятор делителя напряжения «VDR», примеры и приложения
  
• Правила делителя напряжения и тока (VDR и CDR) Уравнения

Правило делителя напряжения для резистивных цепей

Чтобы понять правило резистивного делителя напряжения, возьмем схему, в которой два резистора соединены последовательно с источником напряжения.

Поскольку резисторы соединены последовательно, ток, проходящий через оба резистора, одинаков. Но напряжение не одинаково для обоих резисторов. Входное напряжение схемы делится на оба резистора. А значение отдельного напряжения зависит от сопротивления.

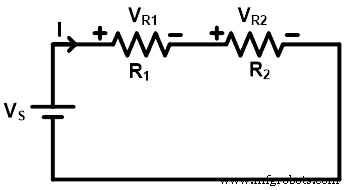
Как показано на рисунке выше, два резистора R₁ и R₂ соединены последовательно с источником напряжения V_s . Суммарный ток, отдаваемый источником, составляет 1 ампер. Поскольку все элементы соединены последовательно, получится один контур, а ток, проходящий через все элементы, будет одинаковым (I ампер).

Напряжение на резисторе R₁ V_R1 а напряжение на резисторе R₂ V_R2 . И общее подаваемое напряжение делится между обоими резисторами. Следовательно, общее напряжение представляет собой сумму V_R1 и V_R2 .

V_S =В _{Р 1} + В _{Р 2} … (1)

В соответствии с законом Ома,

V_R1 =ИК ₁ + ИК ₂ … (2)

Поэтому из уравнения-(1) и (2);

V_S =ИК ₁ + ИК ₂

V_S =I(R ₁ + R ₂ )

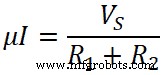
Теперь подставьте значение текущего I в уравнение-(2);

V_R1 =ИК ₁

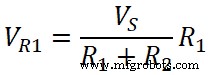
Аналогично;

V_R2 =ИК ₂

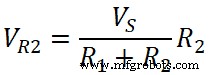
Следовательно, правило делителя напряжения для резистивной цепи противоположно правилу делителя тока. Здесь напряжение резистора представляет собой отношение произведения общего напряжения и этого сопротивления к общему сопротивлению.

Похожие сообщения:

• Теорема Тевенина. Пошаговое руководство с примером решения
• Теорема Нортона. Пошаговое руководство с примером решения

Решенный пример резистивной цепи с использованием VDR

Пример 1

Найдите напряжение на каждом резисторе, используя правило делителя напряжения.

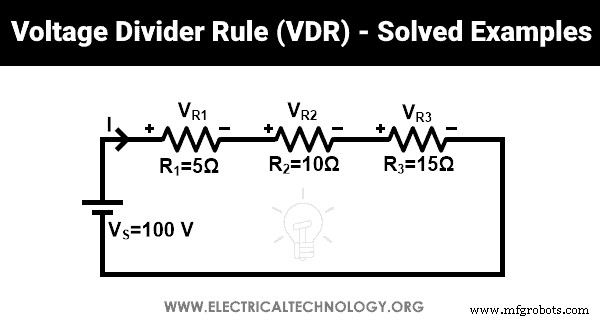
Здесь три резистора (R₁ , R₂ и R₃ ) соединены последовательно с источником напряжения 100В. Напряжение на резисторах R₁ , R₂ и R₃ V_R1 , V_R2 и V_R3 соответственно.

Напряжение на резисторе R₁;

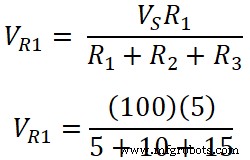
V_{R 3} =500 / 30

V_{R 3} =16,67 В

Напряжение на резисторе R₂;

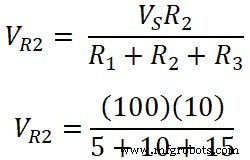
V_{R 3} =100/30

V_{R 3} =33,33 В

Напряжение на резисторе R₃;

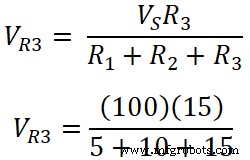
V_{R 3} =1500 / 30

V_{R 3} =50 В

Общее напряжение В_T;

V_T =V _{Р 1} + В _{Р 2} + В _{Р 3}

V_T =16,67 + 33,33 + 50

V _Т =100 В

V_T =В_С

Следовательно, доказано, что общее напряжение=похоже на подаваемое напряжение.

Правило делителя напряжения для индуктивных цепей

Когда цепь с более чем двумя катушками индуктивности соединена последовательно, ток, проходящий через катушки индуктивности, одинаков. Но напряжение источника делится на все катушки индуктивности. В этом случае напряжение на отдельном индукторе можно найти по правилу делителя напряжения индуктора.

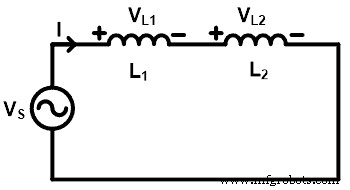
Рассмотрите, как показано на рисунке выше, две катушки индуктивности (L₁ и L₂ ) соединены последовательно. И полный ток I прохожу через индуктор. Напряжение на катушке индуктивности L₁ V_L1 и напряжение на катушке индуктивности L₂ V_L2 . А напряжение питания V_S . Теперь нам нужно найти напряжение V_L1 и V_L2 используя правило делителя напряжения индуктора.

Как мы знаем уравнение напряжения для катушки индуктивности;

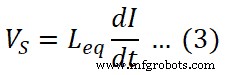
Где L_eq - полная индуктивность цепи. Здесь две катушки индуктивности соединены последовательно. Следовательно, эквивалентная индуктивность представляет собой сумму обеих индуктивностей.

L_eq =Л ₁ + Л ₂

От, уравнение-(3);

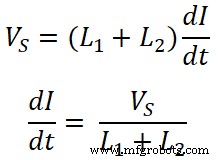
Теперь напряжение на катушке индуктивности L₁ есть;

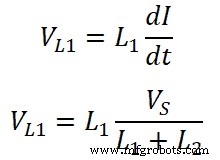
Аналогично, напряжение на катушке индуктивности L₂ есть;

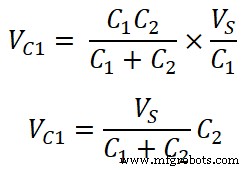
Итак, мы можем сказать, что правило делителя напряжения для катушки индуктивности такое же, как и для резисторов.

Пример решения индуктивной цепи с использованием VDR

Пример 2

Найдите напряжение на каждой катушке индуктивности для данной цепи, используя правило делителя напряжения.

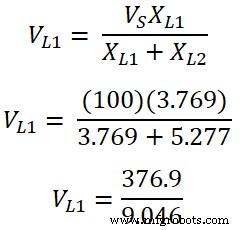
Здесь две катушки индуктивности соединены последовательно с источником 100 В, 60 Гц. Напряжение на катушке индуктивности L₁ V_L1 и напряжение на катушке индуктивности L₂ V_L2 .

Чтобы найти напряжение на катушках индуктивности, нам нужно найти реактивное сопротивление каждой катушки индуктивности.

Реактивное сопротивление катушки индуктивности L₁ есть;

X_{L 1} =2 π f Л₁

X_{L 1} =2 × 3,1415 × 60 × 10 × 10 ^-3

X_{L 1} =3,769 Ом

Реактивное сопротивление катушки индуктивности L₂ есть;

X_{L 2} =2 π f Л₂

X_{L 2} =2 × 3,1415 × 60 × 14 × 10 ^-3

X_{L 2} =5,277 Ом

Согласно правилу делителя напряжения,

Напряжение на катушке индуктивности L₁ есть;

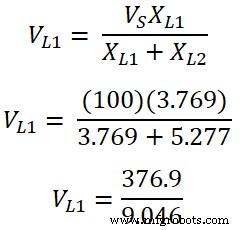
V _{Л 1} =41,66 В

Напряжение на катушке индуктивности L₂ есть;

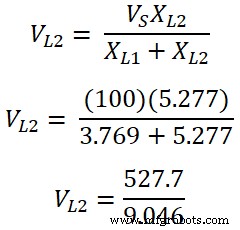
В_{Л 2} =58,35 В

Общее напряжение В_T есть;

V_T =V _{Л 1} + В _L2

V_T =41,66 + 58,35

V _Т =100 В

V_T =В_С

Итак, общее напряжение совпадает с подаваемым напряжением.

Правило делителя напряжения для Емкостный   Схемы

Для конденсатора правило делителя напряжения другое, чем для катушки индуктивности и резистора. Чтобы вычислить правило делителя напряжения для конденсаторов, давайте рассмотрим цепь с двумя или более конденсаторами, соединенными последовательно.

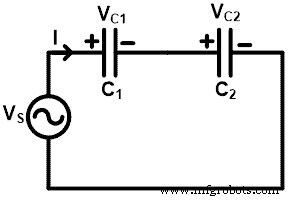
Здесь два конденсатора соединены последовательно с источником напряжения V_S . Напряжение источника делится на два напряжения; одно напряжение на конденсаторе C₁ а второе напряжение подается на конденсатор C₂ .

Напряжение на конденсаторе C₁ V_C1 и напряжение на конденсаторе C₂ V_C2 . Как показано на приведенной выше принципиальной схеме, оба конденсатора соединены последовательно. Следовательно, эквивалентная емкость равна;

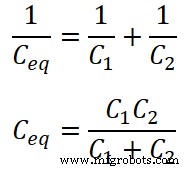
Общая стоимость, предоставленная источником, равна Q;

Вопрос =С _экв. В_С

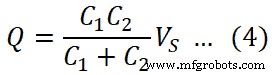
Напряжение на конденсаторе C₁ есть;

V_C1 =В ₁ / С ₁

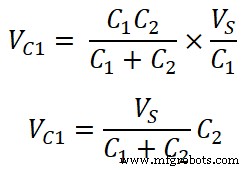
Напряжение на конденсаторе C₂ есть;

V_C2 =В ₁ / С ₂

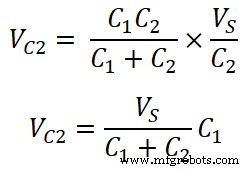
Итак, из расчета мы можем сказать, что отдельное напряжение на конденсаторе представляет собой отношение произведения общего напряжения источника и противоположной емкости к общей емкости.

Пример решенной емкостной цепи с использованием VDR

Пример 3

Найдите напряжение на каждом конденсаторе для данной сети, используя правило делителя напряжения.

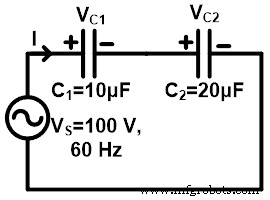
Здесь два конденсатора соединены последовательно с источником 100 В, 60 Гц. Напряжение на конденсаторе C₁ V_C1 и напряжение на конденсаторе C₂ V_C2 .

Чтобы рассчитать напряжение на каждом конденсаторе, нам нужно найти емкостное сопротивление.

Емкостное сопротивление на C₁ есть;

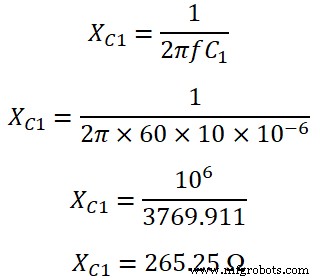
Емкостное сопротивление на C₂ есть;

X _{С 2} =1 / (2 π f С₂ )

X _{С 2} =1 / (2 π × 60 × 20 × 10 ^-6 )

X _{С 2} =10 ^-6 / 7539,822

X _{С 2} =132,63 Ом

Согласно правилу делителя напряжения, напряжение на конденсаторе C₁ есть;

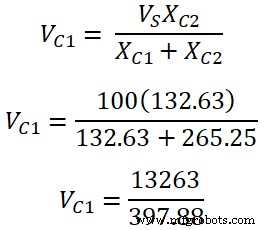
V _C1 =33,33 В

напряжение на конденсаторе C₂ есть;

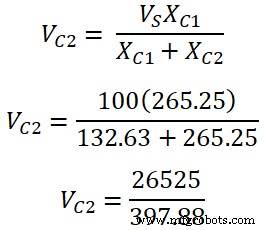
V _{С 2} =66,67 В

Общее напряжение на конденсаторе V_T есть;

V_T =V _{С 1} + В _C2

V_T =33,33 + 66,67

V _Т =100 В

V_T =В_С

Связанные учебные пособия по анализу электрических цепей:

• Анализ схемы SUPERNODE — шаг за шагом с решенным примером
• Анализ схемы SUPERMESH — шаг за шагом с решенным примером
• Калькулятор правила делителя напряжения «VDR» — примеры и приложения
• Калькулятор текущего правила делителя «CDR» — примеры и приложения
• Закон Кирхгофа о токе и напряжении (KCL и KVL) | Решенный пример
• Калькулятор по правилу Крамера – система из 2 и 3 уравнений для электрических цепей
• Мост Уитстона — схема, работа, происхождение и применение
• Калькуляторы для электротехники и электроники
• 5000+ формул и уравнений для электротехники и электроники