MATLAB — Дифференциал
MATLAB предоставляет diff команда для вычисления символьных производных. В простейшей форме вы передаете функцию, которую хотите отличить, в команду diff в качестве аргумента.
Например, вычислим производную функции f(t) =3t 2 + 2t -2
Пример
Создайте файл сценария и введите в него следующий код —
syms t f = 3*t^2 + 2*t^(-2); diff(f)
Когда приведенный выше код скомпилирован и выполнен, он дает следующий результат —
ans = 6*t - 4/t^3
Ниже приведен октавный эквивалент приведенного выше расчета —
pkg load symbolic
symbols
t = sym("t");
f = 3*t^2 + 2*t^(-2);
differentiate(f,t)
Octave выполняет код и возвращает следующий результат —
ans = -(4.0)*t^(-3.0)+(6.0)*t
Проверка элементарных правил дифференциации
Сформулируем кратко различные уравнения или правила дифференцирования функций и проверим эти правила. Для этого мы будем писать f'(x) для производной первого порядка и f"(x) для производной второго порядка.
Ниже приведены правила дифференциации —
Правило 1
Для любых функций f и g и любых действительных чисел a и b являются производными функции -
h(x) =af(x) + bg(x) относительно x задается -
h'(x) =af'(x) + bg'(x)
Правило 2
сумма и вычитание Правила гласят, что если f и g — две функции, f' и g' — их производные соответственно, то
(f + g)' =f' + g'
(f - g)' =f' - g'
Правило 3
продукт Правило гласит, что если f и g — две функции, f' и g' — их производные соответственно, то
(f.g)' =f'.g + g'.f
Правило 4
Коэффициент Правило гласит, что если f и g — две функции, f' и g' — их производные соответственно, то
(f/g)' =(f'.g - g'.f)/g 2
Правило 5
Полином или правило элементарной мощности утверждает, что если y =f(x) =x n , то f' =n. х (n-1)
Прямым следствием этого правила является то, что производная любой константы равна нулю, т. е. если y =k , любая константа, то
f' =0
Правило 6
цепочка правило гласит, что производная функции функции h(x) =f(g(x)) относительно x,
h'(x)=f'(g(x)).g'(x)
Пример
Создайте файл сценария и введите в него следующий код —
syms x syms t f = (x + 2)*(x^2 + 3) der1 = diff(f) f = (t^2 + 3)*(sqrt(t) + t^3) der2 = diff(f) f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2) der3 = diff(f) f = (2*x^2 + 3*x)/(x^3 + 1) der4 = diff(f) f = (x^2 + 1)^17 der5 = diff(f) f = (t^3 + 3* t^2 + 5*t -9)^(-6) der6 = diff(f)
Когда вы запускаете файл, MATLAB отображает следующий результат —
f = (x^2 + 3)*(x + 2) der1 = 2*x*(x + 2) + x^2 + 3 f = (t^(1/2) + t^3)*(t^2 + 3) der2 = (t^2 + 3)*(3*t^2 + 1/(2*t^(1/2))) + 2*t*(t^(1/2) + t^3) f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2) der3 = (2*x - 2)*(3*x^3 - 5*x^2 + 2) - (- 9*x^2 + 10*x)*(x^2 - 2*x + 1) f = (2*x^2 + 3*x)/(x^3 + 1) der4 = (4*x + 3)/(x^3 + 1) - (3*x^2*(2*x^2 + 3*x))/(x^3 + 1)^2 f = (x^2 + 1)^17 der5 = 34*x*(x^2 + 1)^16 f = 1/(t^3 + 3*t^2 + 5*t - 9)^6 der6 = -(6*(3*t^2 + 6*t + 5))/(t^3 + 3*t^2 + 5*t - 9)^7
Ниже приведен октавный эквивалент приведенного выше расчета —
pkg load symbolic
symbols
x = sym("x");
t = sym("t");
f = (x + 2)*(x^2 + 3)
der1 = differentiate(f,x)
f = (t^2 + 3)*(t^(1/2) + t^3)
der2 = differentiate(f,t)
f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)
der3 = differentiate(f,x)
f = (2*x^2 + 3*x)/(x^3 + 1)
der4 = differentiate(f,x)
f = (x^2 + 1)^17
der5 = differentiate(f,x)
f = (t^3 + 3* t^2 + 5*t -9)^(-6)
der6 = differentiate(f,t)
Octave выполняет код и возвращает следующий результат —
f = (2.0+x)*(3.0+x^(2.0)) der1 = 3.0+x^(2.0)+(2.0)*(2.0+x)*x f = (t^(3.0)+sqrt(t))*(3.0+t^(2.0)) der2 = (2.0)*(t^(3.0)+sqrt(t))*t+((3.0)*t^(2.0)+(0.5)*t^(-0.5))*(3.0+t^(2.0)) f = (1.0+x^(2.0)-(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0)) der3 = (-2.0+(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0))+((9.0)*x^(2.0)-(10.0)*x)*(1.0+x^(2.0)-(2.0)*x) f = (1.0+x^(3.0))^(-1)*((2.0)*x^(2.0)+(3.0)*x) der4 = (1.0+x^(3.0))^(-1)*(3.0+(4.0)*x)-(3.0)*(1.0+x^(3.0))^(-2)*x^(2.0)*((2.0)*x^(2.0)+(3.0)*x) f = (1.0+x^(2.0))^(17.0) der5 = (34.0)*(1.0+x^(2.0))^(16.0)*x f = (-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-6.0) der6 = -(6.0)*(-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-7.0)*(5.0+(3.0)*t^(2.0)+(6.0)*t)
Производные показательной, логарифмической и тригонометрической функций
В следующей таблице представлены производные обычно используемых экспоненциальных, логарифмических и тригонометрических функций —
| Функция | Производный |
|---|---|
| c a.x | c a.x .ln c.a (ln — натуральный логарифм) |
| е х | е х |
| длина x | 1/x |
| лнc х | 1/x.ln c |
| х х | х х .(1 + ln x) |
| sin(x) | cos(x) |
| cos(x) | -sin(x) |
| загар(х) | сек 2 (x) или 1/cos 2 (x) или 1 + tan 2 (х) |
| детская кроватка(x) | -csc 2 (x) или -1/sin 2 (x) или -(1 + кроватка 2 (х)) |
| сек(х) | sec(x).tan(x) |
| csc(x) | -csc(x).cot(x) |
Пример
Создайте файл сценария и введите в него следующий код —
syms x y = exp(x) diff(y) y = x^9 diff(y) y = sin(x) diff(y) y = tan(x) diff(y) y = cos(x) diff(y) y = log(x) diff(y) y = log10(x) diff(y) y = sin(x)^2 diff(y) y = cos(3*x^2 + 2*x + 1) diff(y) y = exp(x)/sin(x) diff(y)
Когда вы запускаете файл, MATLAB отображает следующий результат —
y = exp(x) ans = exp(x) y = x^9 ans = 9*x^8 y = sin(x) ans = cos(x) y = tan(x) ans = tan(x)^2 + 1 y = cos(x) ans = -sin(x) y = log(x) ans = 1/x y = log(x)/log(10) ans = 1/(x*log(10)) y = sin(x)^2 ans = 2*cos(x)*sin(x) y = cos(3*x^2 + 2*x + 1) ans = -sin(3*x^2 + 2*x + 1)*(6*x + 2) y = exp(x)/sin(x) ans = exp(x)/sin(x) - (exp(x)*cos(x))/sin(x)^2
Ниже приведен октавный эквивалент приведенного выше расчета —
pkg load symbolic
symbols
x = sym("x");
y = Exp(x)
differentiate(y,x)
y = x^9
differentiate(y,x)
y = Sin(x)
differentiate(y,x)
y = Tan(x)
differentiate(y,x)
y = Cos(x)
differentiate(y,x)
y = Log(x)
differentiate(y,x)
% symbolic packages does not have this support
%y = Log10(x)
%differentiate(y,x)
y = Sin(x)^2
differentiate(y,x)
y = Cos(3*x^2 + 2*x + 1)
differentiate(y,x)
y = Exp(x)/Sin(x)
differentiate(y,x)
Octave выполняет код и возвращает следующий результат —
y = exp(x) ans = exp(x) y = x^(9.0) ans = (9.0)*x^(8.0) y = sin(x) ans = cos(x) y = tan(x) ans = 1+tan(x)^2 y = cos(x) ans = -sin(x) y = log(x) ans = x^(-1) y = sin(x)^(2.0) ans = (2.0)*sin(x)*cos(x) y = cos(1.0+(2.0)*x+(3.0)*x^(2.0)) ans = -(2.0+(6.0)*x)*sin(1.0+(2.0)*x+(3.0)*x^(2.0)) y = sin(x)^(-1)*exp(x) ans = sin(x)^(-1)*exp(x)-sin(x)^(-2)*cos(x)*exp(x)
Вычисление производных высших порядков
Чтобы вычислить высшие производные функции f, мы используем синтаксис diff(f,n) .
Вычислим вторую производную функции y =f(x) =x .e -3x
f = x*exp(-3*x); diff(f, 2)
MATLAB выполняет код и возвращает следующий результат —
ans = 9*x*exp(-3*x) - 6*exp(-3*x)
Ниже приведен октавный эквивалент приведенного выше расчета —
pkg load symbolic
symbols
x = sym("x");
f = x*Exp(-3*x);
differentiate(f, x, 2)
Octave выполняет код и возвращает следующий результат —
ans = (9.0)*exp(-(3.0)*x)*x-(6.0)*exp(-(3.0)*x)
Пример
В этом примере давайте решим задачу. Учитывая, что функция y =f(x) =3 sin(x) + 7 cos(5x) . Нам нужно выяснить, верно ли уравнение f" + f =-5cos(2x). верно.
Создайте файл сценария и введите в него следующий код —
syms x
y = 3*sin(x)+7*cos(5*x); % defining the function
lhs = diff(y,2)+y; %evaluting the lhs of the equation
rhs = -5*cos(2*x); %rhs of the equation
if(isequal(lhs,rhs))
disp('Yes, the equation holds true');
else
disp('No, the equation does not hold true');
end
disp('Value of LHS is: '), disp(lhs);
Когда вы запускаете файл, он отображает следующий результат —
No, the equation does not hold true Value of LHS is: -168*cos(5*x)
Ниже приведен октавный эквивалент приведенного выше расчета —
pkg load symbolic
symbols
x = sym("x");
y = 3*Sin(x)+7*Cos(5*x); % defining the function
lhs = differentiate(y, x, 2) + y; %evaluting the lhs of the equation
rhs = -5*Cos(2*x); %rhs of the equation
if(lhs == rhs)
disp('Yes, the equation holds true');
else
disp('No, the equation does not hold true');
end
disp('Value of LHS is: '), disp(lhs);
Octave выполняет код и возвращает следующий результат —
No, the equation does not hold true Value of LHS is: -(168.0)*cos((5.0)*x)
Поиск максимума и минимума кривой
Если мы ищем локальные максимумы и минимумы для графика, мы в основном ищем самые высокие или самые низкие точки на графике функции в определенной местности или для определенного диапазона значений символической переменной.
Для функции y =f(x) точки на графике, в которых график имеет нулевой наклон, называются стационарными точками . Другими словами, стационарные точки находятся там, где f'(x) =0.
Чтобы найти точки покоя функции, которую мы дифференцируем, нам нужно приравнять производную к нулю и решить уравнение.
Пример
Найдем точки покоя функции f(x) =2x 3 + 3x 2 − 12x + 17
Выполните следующие шаги —
Давайте сначала введем функцию и построим ее график.
syms x y = 2*x^3 + 3*x^2 - 12*x + 17; % defining the function ezplot(y)
MATLAB выполняет код и возвращает следующий график —
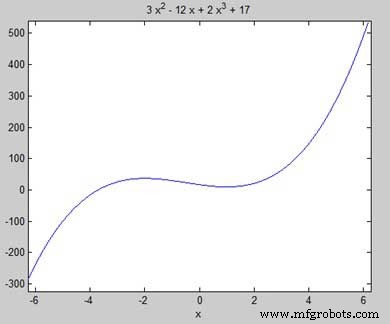
Вот эквивалентный код Octave для приведенного выше примера —
pkg load symbolic
symbols
x = sym('x');
y = inline("2*x^3 + 3*x^2 - 12*x + 17");
ezplot(y)
print -deps graph.eps
Наша цель — найти локальные максимумы и минимумы на графике, поэтому давайте найдем локальные максимумы и минимумы для интервала [-2, 2] на графике.
syms x y = 2*x^3 + 3*x^2 - 12*x + 17; % defining the function ezplot(y, [-2, 2])
MATLAB выполняет код и возвращает следующий график —
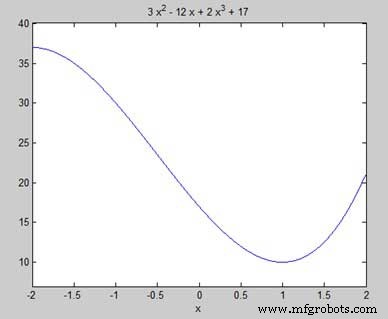
Вот эквивалентный код Octave для приведенного выше примера —
pkg load symbolic
symbols
x = sym('x');
y = inline("2*x^3 + 3*x^2 - 12*x + 17");
ezplot(y, [-2, 2])
print -deps graph.eps
Далее вычислим производную.
g = diff(y)
MATLAB выполняет код и возвращает следующий результат —
g = 6*x^2 + 6*x - 12
Вот октавный эквивалент приведенного выше расчета —
pkg load symbolic
symbols
x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)
Octave выполняет код и возвращает следующий результат —
g = -12.0+(6.0)*x+(6.0)*x^(2.0)
Давайте решим функцию производной g, чтобы получить значения, при которых она становится равной нулю.
s = solve(g)
MATLAB выполняет код и возвращает следующий результат —
s = 1 -2
Ниже приведен октавный эквивалент приведенного выше расчета —
pkg load symbolic
symbols
x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)
roots([6, 6, -12])
Octave выполняет код и возвращает следующий результат —
g = -12.0+(6.0)*x^(2.0)+(6.0)*x ans = -2 1
Это согласуется с нашим сюжетом. Итак, оценим функцию f в критических точках x =1, -2. Мы можем заменить значение в символьной функции, используя subs команда.
subs(y, 1), subs(y, -2)
MATLAB выполняет код и возвращает следующий результат —
ans = 10 ans = 37
Ниже приведен октавный эквивалент приведенного выше расчета —
pkg load symbolic
symbols
x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)
roots([6, 6, -12])
subs(y, x, 1), subs(y, x, -2)
ans = 10.0 ans = 37.0-4.6734207789940138748E-18*I
Следовательно, минимальное и максимальное значения функции f(x) =2x 3 + 3x 2 − 12x + 17, в интервале [-2,2] находятся 10 и 37.
Решение дифференциальных уравнений
MATLAB предоставляет dsolve команда для символьного решения дифференциальных уравнений.
Самая основная форма dsolve команда для нахождения решения одного уравнения
dsolve('eqn')
где уравнение это текстовая строка, используемая для ввода уравнения.
Он возвращает символьное решение с набором произвольных констант, которые MATLAB помечает как C1, C2 и т. д.
Вы также можете указать начальные и граничные условия для задачи в виде списка, разделенного запятыми, следующего за уравнением как -
dsolve('eqn','cond1', 'cond2',…)
Для использования команды dsolve производные обозначаются буквой D . Например, такое уравнение, как f'(t) =-2*f + cost(t), вводится как -
'Df =-2*f + cos(t)'
Более высокие производные обозначаются буквой D после порядка производной.
Например, уравнение f"(x) + 2f'(x) =5sin3x должно быть введено как -
'D2y + 2Dy =5*sin(3*x)'
Возьмем простой пример дифференциального уравнения первого порядка:y' =5y.
s = dsolve('Dy = 5*y')
MATLAB выполняет код и возвращает следующий результат —
s = C2*exp(5*t)
Возьмем другой пример дифференциального уравнения второго порядка:y" - y =0, y(0) =-1, y'(0) =2.
dsolve('D2y - y = 0','y(0) = -1','Dy(0) = 2')
MATLAB выполняет код и возвращает следующий результат —
ans = exp(t)/2 - (3*exp(-t))/2
MATLAB



