Электроуправляемое псевдомагнетосопротивление долины в графене с Y-образным искажением решетки Кекуле
Аннотация
Мы предлагаем новый метод регулирования долинного псевдомагнетосопротивления в полевых полевых транзисторах на основе баллистического графена с учетом Y-образного искажения решетки Кекуле и электрического барьера. Устройство включает инжекцию впадин и обнаружение впадин источником и стоком ферромагнитной деформации. Управление долиной в канале достигается за счет Y-образного искажения решетки Кекуле и электрического барьера. Центральный механизм этих устройств основан на Y-образной форме искажения решетки Кекуле в графене, которая может вызвать прецессию впадины, тем самым управляя ориентацией впадин электронов канала и, следовательно, током, собираемым на стоке. Мы обнаружили, что настраиваемое внешнее напряжение смещения заставляет псевдомагнетосопротивление долины колебаться между положительными и отрицательными значениями, и может быть достигнуто колоссальное псевдомагнетосопротивление туннельной долины более 30 000%. Наши результаты показывают, что синергия Valleytronics и цифровой логики может предоставить новые парадигмы для обработки информации на основе Valleytronic и обратимых вычислений.
Введение
Графен, представляющий собой двумерный слой атомов углерода, который обладает превосходной подвижностью носителей и предлагает максимально тонкий канал для использования в конструкции полевых транзисторов металл-оксид-полупроводник [1]. Семенов предложил спиновый полевой транзистор с использованием слоя графена в качестве канала [2], который включает инжекцию спина и обнаружение спина ферромагнитным источником и стоком, а манипуляция спином в канале достигается посредством электрического управления электронным обменом. взаимодействие с ферромагнитным затвором. Кроме того, спин-орбитальное взаимодействие Рашбы - еще один многообещающий инструмент для управления спином в графене [3]. Спин-орбитальное взаимодействие Рашбы может вызывать прецессию спина, контролируя, таким образом, ориентацию спинов канальных электронов. Спиновые полевые транзисторы также вдохновили на многие важные исследовательские идеи, такие как гигантское магнитосопротивление и туннельное магнитосопротивление [3, 4]. Гигантское магнитосопротивление и туннельное магнитосопротивление можно применять в технологиях цифровой памяти и магнитных датчиков.
С другой стороны, электроны Дирака в графене обладают дополнительной долиной степени свободы помимо обычных зарядовых и спиновых аналогов. Из-за большой разницы в импульсе между двумя долинами и подавления междолинного рассеяния в чистых образцах графена [5–7] считается, что степень свободы долины оказывает тот же эффект, что и спин электрона, при переносе и манипулировании информацией, что ведет к появлению новой дисциплины вальтроники. В качестве аналога спинового полевого транзистора, полевой транзистор долины также теоретически предлагается в графене [8], который состоит из квантового одномерного канала графена с зазором, зажатого между двумя кресельными графеновыми нанолентами (истоком и стоком); затем электрическое поле бокового затвора прикладывается к каналу и модулирует поляризацию впадины носителей из-за взаимодействия впадины и орбиты, таким образом управляя величиной тока, собираемого на стоке. Однако из-за того, что связь долин в графене долгое время не стала физической реальностью, дальнейших исследований, основанных на полевых транзисторах графена долины, и связанных с ними исследований мало. Недавние эксперименты Gutierrez et al. [9] обнаружили необычную Y-образную текстуру связи Кекуле (Kek-Y) в сотовой решетке на сверхрешетке графен-медь, где один из шести атомов углерода в каждой элементарной ячейке сверхрешетки не имеет атомов меди под ней и приобретает более короткий связь ближайшего соседа. Кроме того, Гамаюн показал, что текстура связи Kek-Y предлагает путь для управляемой импульсом прецессии долины [10]. Beenakker et al. [11] показали, что система Кека может вызывать эффект переворота долины через андреевское отражение. Rencently Wang et al. [12] обнаружили, что модуляция длины связи C-C решетки Кекуле, которая поддерживает инверсионную симметрию системы, может использоваться для управления степенью свободы долины аналогично прецессирующему спину обменного поля. Это позволяет создать новый тип долинного полевого транзистора в графене. Более того, нет сообщений о совместном влиянии искажения решетки Кека-Y на псевдомагнетосопротивление долин в графене. Псевдомагнетосопротивление долины [13, 14] аналогично магнитосопротивлению в магнитном туннельном переходе [15], где величина спинового тока зависит от магнитной ориентации электродов [4].
Методы
В данной работе мы предлагаем новый тип долинных полевых транзисторов (VFET) для электронов на основе графена. Конструкция устройства предполагает наличие источника / стока ферромагнитной деформации (FM-S) для впрыска / детектирования с поляризованной долиной поляризации, что напоминает обычный спиновый транзистор (см. Рис. 1a). Вращение долины в канале графена основано на сверхрешетке графена Kek-Y [10–12], которая может быть достигнута с помощью сверхрешетки графена, эпитаксиально выращенной на Cu (111), при этом атомы меди совпадают с атомами углерода [9]. Однако атомы меди отсутствуют под некоторыми атомами углерода, в результате чего некоторые периодические вакансии атомов меди появляются под графеном. Такая вакансия атома подложки приводит к сжатию трех соседних связей. Здесь мы используем δ т чтобы представить изменение энергии прыжка электрона, соответствующего этим трем связям. Мы предполагаем, что ферромагнитный графен состоит из той же металлической полосы FM. Две намагниченности истока и стока направлены вдоль направления тока ( x оси), которые могут быть либо в параллельном (P), либо в антипараллельном (AP) положении, с помощью внешнего магнитного поля в плоскости. В калибровке Ландау магнитный векторный потенциал, возникающий из краевого поля, имеет вид [16, 17] \ (A (r) =A_ {y} (x) \ overrightarrow {y} \) с A y ( x ) = А y [ Θ (- x ) ± Θ ( x - L )], где знак плюс (минус) соответствует P (AP) конфигурации намагниченностей, Θ ( x ) - ступенчатая функция Хевисайда. С другой стороны, мы предполагаем, что на исток и сток полевых транзисторов действует одинаковая нагрузка, которая может быть вызвана натяжением подложки из графена [18]. Упругая деформация может рассматриваться как возмущение амплитуд прыжков и действует как калибровочный потенциал A S ( г ). Натяжение задается по x направление, в данном случае A S ( г ) равномерное по y ось [16]. Для определенности возьмем типичный гладкий профиль его y компонент как A Sy ( x ) = А S [ Θ (- x ) + Θ ( x - L )], где A S это амплитуда. Кроме того, в области решетки Kek-Y применяется электрический барьер, который можно регулировать внешним напряжением смещения.
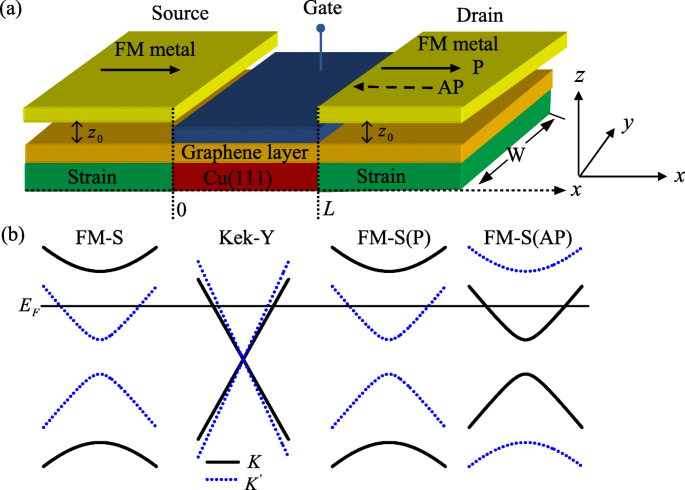
а Схематическое изображение VFET, использующего канал графена с искажением решетки Kek-Y и смещением затвора, которое контролирует ориентацию впадины электронов канала. Исток и сток - это графен FM-S, который инжектирует и детектирует электроны с определенной поляризацией. Где z 0 - расстояние между слоем графена и полосой FM. L длина канала, Вт ширина образца графена в y направление и W ≫ L . б Ленточная структура вблизи точек Дирака. Горизонтальная линия обозначает энергию Ферми (цвет онлайн)
Распространение низкоэнергетических возбуждающих квазичастиц в полевых транзисторах со сверхрешетками графена Kek-Y можно описать следующим одночастичным гамильтонианом [10–12]
$$ \ begin {array} [c] {ll} H =&v_ {F} (\ mathbf {P} \ cdot \ sigma) + v _ {\ tau} (\ mathbf {P} \ cdot \ tau) \ Theta \ left (x \ right) \ Theta \ left (Lx \ right) + \\ &U \ sigma_ {0} \ tau_ {0} \ Theta \ left (x \ right) \ Theta \ left (Lx \ right) + A_ {M} (x) \ sigma_ {y} + \ tau_ {z} A_ {S} (x) \ sigma_ {y}. \ end {массив} $$ (1)Здесь σ и τ - матрицы Паули для подрешетки и долины соответственно. P =( p x , p y ) - импульс безмассовых дираковских электронов, τ z =± 1 для K и \ (K ^ {^ {\ prime}} \) долины, v F =10 6 м / с - скорость дираковских электронов в чистом графене, а v τ ≃ v F δ т / 3 t - член модификации скорости из-за эффекта сжатия связи в решетке Кека-Y [12], где t - энергия прыжка между ближайшими соседними центрами для чистого графена. U - настраиваемый затвором потенциальный барьер. А M ( x ) = e v F А y ( x ) [19]. Собственные значения гамильтониана в графене с искажением решетки Кека и электрическим барьером имеют вид
$$ E _ {\ alpha, \ beta} =U + \ alpha (\ hbar v_ {F} + \ beta \ hbar v _ {\ tau}) \ sqrt {k_ {x \ beta} ^ {2} + k_ {y} ^ {2}}. $$ (2)Здесь α =+ 1 (−1) определяет зону проводимости (валентную). β =± 1 обозначает две разделенные долиной подзоны зоны проводимости и валентной зоны. Из-за трансляционной инвариантности в y направление, поперечный волновой вектор k y сохраняется. Собственные состояния в графене с однородным искажением решетки Кека-Y характеризуются выражением \ (\ Psi _ {\ beta} ^ {\ pm} (k_ {x \ beta}, k_ {y}) =\ frac {1} { N _ {\ beta}} \ left (1, P _ {\ beta} ^ {\ pm}, Q _ {\ beta} ^ {\ pm}, R _ {\ beta} ^ {\ pm} \ right) ^ {T} \), где N β - константа нормализации \ (N _ {\ beta} =\ left (1 + P _ {\ beta} ^ {2} + Q _ {\ beta} ^ {2} + R _ {\ beta} ^ {2} \ right) ^ {\ frac {1} {2}} \) и \ (P _ {\ beta} ^ {\ pm}, Q _ {\ beta} ^ {\ pm} \) и \ (R _ {\ beta} ^ {\ pm} \) - это функции, определенные следующим образом:
$$ \ begin {array} [c] {cc} P _ {\ beta} ^ {\ pm} =&\ frac {(EU) ^ {2} + \ left (\ hbar ^ {2} v_ {F} ^ {2} - \ hbar ^ {2} v _ {\ tau} ^ {2} \ right) \ left (k_ {x \ beta} ^ {2} + k_ {y} ^ {2} \ right)} {2 (ЕС) \ hbar v_ {F} (\ pm k_ {x \ beta} - {ik} _ {y})}, \\ Q _ {\ beta} ^ {\ pm} =&\ frac {(EU) ^ {2} - \ left (\ hbar ^ {2} v_ {F} ^ {2} - \ hbar ^ {2} v _ {\ tau} ^ {2} \ right) \ left (k_ {x \ beta} ^ {2} + k_ {y} ^ {2} \ right)} {2 (EU) \ hbar v _ {\ tau} (\ pm k_ {x \ beta} - {ik} _ {y})}, \\ R _ {\ beta} ^ {\ pm} =&\ frac {(EU) ^ {2} - \ left (\ hbar ^ {2} v_ {F} ^ {2} + \ hbar ^ {2} v _ {\ tau} ^ {2} \ right) \ left (k_ {x \ beta} ^ {2} + k_ {y} ^ {2} \ right)} {2 \ hbar ^ {2} v_ {F} v _ {\ tau} (\ pm k_ {x \ beta} - {ik} _ {y}) ^ {2}}. \ конец {массив} $$ (3)Вероятность передачи из долины \ (K ^ {^ {\ prime}} \) в долину \ (K (K ^ {^ {\ prime}}) \) \ (T_ {K ^ {^ {\ prime}}, K (K ^ {^ {\ prime}})} \) можно вычислить, используя метод матрицы передачи [20]. Согласно формуле Лаудауэра-Бтиттикера проводимость, зависящая от долины, определяется как [21]:
$$ G_ {K ^ {^ {\ prime}}, K (K ^ {^ {\ prime}})} =G_ {0} {\ int _ {- \ frac {\ pi} {2}} ^ {\ гидроразрыв {\ pi} {2}}} T_ {K ^ {^ {\ prime}}, K (K ^ {^ {\ prime}})} \ cos (\ phi_ {0}) d \ phi_ {0} . $$ (4)Здесь \ (G_ {0} =2e ^ {2} W / \ left (v_ {F} \ pi ^ {2} \ hbar ^ {2} \ right) \ left \ vert E \ right \ vert \), W ширина образца графена в y направление и ϕ 0 угол падения относительно x направление.
Прежде чем приступить к расчетам, обсудим зонную структуру с k y =0, как показано на рис. 1б. В области источника FM-S энергетическая зона графена записывается как \ (E =\ alpha \ sqrt {(\ hbar v_ {F} k_ {x}) ^ {2} + (A_ {M} + \ tau _ {z} A_ {S}) ^ {2}} \). Можно обнаружить, что вырожденная долина является подъемной, и при K индуцируются различные зазоры. и \ (K ^ {^ {\ prime}}} \) указывает, потому что полный векторный потенциал A M + A S действует на K электронов выше полного векторного потенциала | A M - А S | действующее на \ (K ^ {^ {\ prime}}} \) электроны [19]. Это означает, что только \ (K ^ {^ {\ prime}} \) электроны могут проходить через область источника FM-S, когда падающая энергия находится в | A M - А S | < E < А M + A S [22, 23]. Точно так же в области стока FM-S энергетическая зона графена может быть записана как \ (E =\ alpha \ sqrt {(\ hbar v_ {F} k_ {x}) ^ {2} + (\ pm A_ { M} + \ tau _ {z} A_ {S}) ^ {2}} \), где знак ± соответствует P- и AP-конфигурации намагниченностей. Таким образом, только \ (K ^ {^ {\ prime}}} \) электроны обнаруживаются в P-структуре и только K электроны обнаруживаются в AP-структуре, когда энергия Ферми находится в диапазоне [| A M - А S |, А M + A S ]. В канале графена вырожденная долина - это тоже подъем, но есть важное отличие. В отличие от свинцового случая, где фазы K и компоненты \ (K ^ {^ {\ prime}} \) развиваются с одним и тем же волновым вектором [т.е. \ (k =E / \ hbar v_ {F} \)], теперь они развиваются отдельно с разными волновыми векторами ( \ (k _ {+} =(EU) / (\ hbar v_ {F} + \ hbar v _ {\ tau}) \) и \ (k _ {-} =(EU) / (\ hbar v_ {F} - \ hbar v _ {\ tau}) \)) из-за графеновых сверхрешеток Kek-Y, перемешивающих долину (см. уравнение 2). Это приводит к долинной прецессии канальных электронов в долинном пространстве [12]. Прецессия долины в графене является основой полевого транзистора долины [8]. И прецессия долины также может быть охарактеризована псевдомагнетосопротивлением долины (VPMR) в переходах FM-S / Kek-Y / FM-S, аналогичным магнитосопротивлению в квантовых туннельных переходах на основе графена со спин-орбитальным взаимодействием [4] , который определяется как \ (VPMR =\ frac {G_ {P} -G_ {AP}} {G_ {P}} \), где G P и G AP представляют проводимость в конфигурациях P и AP, соответственно, и \ (G_ {P} =G_ {K ^ {^ {\ prime}}, K ^ {^ {\ prime}}}, G_ {AP} =G_ {K ^ {^ {\ prime}}, K} \). Величина тока впадины зависит от магнитной ориентации истока и стока в рассматриваемом нами устройстве.
Числовые результаты и обсуждения
Ниже мы представляем численные результаты для перехода FM-S / Kek-Y / FM-S в графене. На протяжении всей статьи мы устанавливаем длину канала L . =207 нм, и ограничить энергию Ферми 20 мэВ < E <140 мэВ, предполагается, что он удовлетворяет | A M - А S | < E < А M + A S . На рисунках 2a и b показаны результаты расчета туннельной проводимости и VPMR как функции v . т с энергией Ферми E =80 мэВ и прямоугольный потенциальный барьер U =-10 мэВ. Мы можем найти, что G P и G AP имеют те же периоды колебаний, но обратные фазы. Следовательно, VPMR колеблется с увеличением v т и может появиться отрицательное значение VPMR. Эти явления аналогичны случаю магнитосопротивления в квантовых туннельных переходах на основе баллистического графена со спин-орбитальным взаимодействием [4]. Колебательные характеристики проводимости G P и G AP можно объяснить разностью фаз между двумя составляющими долины. Когда угол падения ϕ 0 =0, фазовый сдвиг определяется как:\ (\ Delta \ theta =(k_ {x +} - k_ {x -}) L =- \ frac {2 (EU) v _ {\ tau}} {\ hbar (v_ {F} ^ {2} -v _ {\ tau} ^ {2})} L \). Δ θ определяет ориентацию поляризации долины перед тем, как электрон попадает в сток, относительно ориентации состояния стока [8]. Для Δ θ =± 2 n π , n =1,2,3 ⋯, две поляризации выровнены, что приводит к проводимости G P максимум и VPMR - высокое положительное значение (как показано в v τ =0,022, 0,033). С другой стороны, для Δ θ =± (2 n +1) π , n =0,1,2 ⋯, они ортогональны друг другу, что приводит к проводимости G AP минимальный и отрицательный VPMR (как показано в v τ =0,0167, 0,027, 0,038).
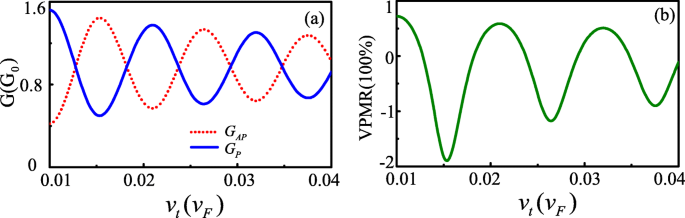
Поведение G P , А P и VPMR по сравнению с v т в L =207 нм, E =80 мэВ и U =−10 мэВ (цвет онлайн)
Проводимость и VPMR являются не только осцилляционными функциями модификации энергии прыжка, они также осциллируют вместе с энергией Ферми и эффективным барьерным потенциалом, поскольку Δ θ масштабы также линейны с энергией Ферми и потенциальным барьером U . На рис. 3а и б показаны зависимости проводимости от энергии Ферми и эффективного барьерного потенциала соответственно. Соответствующие VPMR показаны на рис. 3c и d. Все они показывают колебательные характеристики, изменяющиеся на E и U значение, даже когда эффективный барьерный потенциал U больше энергии Ферми E . Физическая причина такого явления связана с туннелированием Клейна [12]. Хотя есть аналогичные явления осцилляции проводимости и VPMR для увеличенного E и U , также могут быть обнаружены некоторые отличия. Как E увеличивается, разница между G P и G AP проводимость становится все меньше и меньше, что приводит к тому, что амплитуда колебаний VPMR уменьшается с увеличением энергии Ферми. При условии Δ θ =± n π выполнено, разница между G P и G AP тем больше, чем больше U , особенно в некоторых местах, G P и G AP проводимость представляет характеристики переключения. Персонажи более желательны для применения VPMR. Примечательно, что наблюдаемое максимальное значение VPMR составляет более 30 000% при малых E . Это значение значительно превышает MR ~ 175 % в квантовых туннельных переходах на основе баллистического графена со спин-орбитальным взаимодействием [4] и псевдомагнетосопротивлением ~ 100 % в двухслойном графене, управляемом внешними вентилями [24], что даже больше, чем VPMR ~ 10000 % в системе сливающихся конусов Дирака [13].
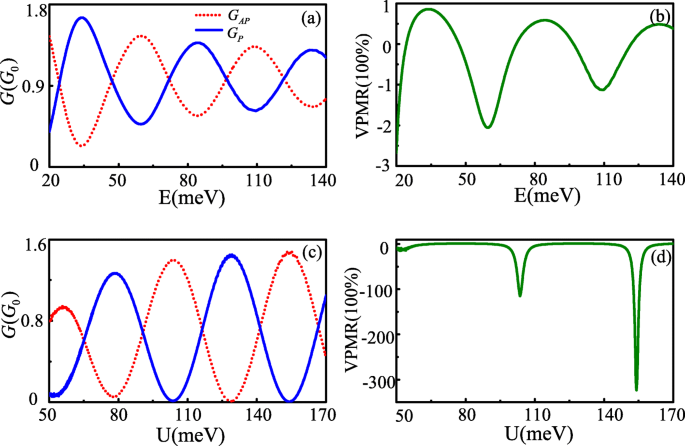
Поведение G P , А P ( а , c ) и VPMR ( b , d ) как функции энергии Ферми и электрического барьера при L =207 нм, v т =0,02 v f . остальные параметры: U =−10 мэВ для a и c , E =80 мэВ для b и d (цвет онлайн)
Выводы
В заключение мы предложили тип долинных полевых транзисторов для электрона на основе графена и исследовали через него долинное псевдомагнетосопротивление. Мы показали, что осцилляционная особенность долинного псевдомагнетосопротивления связана не только с модификацией энергии прыжка и энергией Ферми, но также может быть настроена в значительной степени за счет эффективного барьерного потенциала. Псевдомагнетосопротивление долины, настраиваемое внешним напряжением смещения, приносит пользу устройству полевого транзистора долины, и мы ожидаем, что предложенные здесь квантовые устройства долины с электрическим управлением могут сыграть роль в квантовых и квантово-классических гибридных компьютерах.
Дальнейшие исследования могут включать различную деформацию (одноосную или двухосную), регулирующую долинное рассеяние электронов и транспорт в предлагаемых нами полевых полевых транзисторах на основе графена, поскольку окрашивание полезно для контроля степени междолинного рассеяния в диаграммах Кекуле [25]. . Затем другие двухмерные материалы (MoS 2 , WS 2 , WSe 2 и т. д.) аналоги в графене могут также обеспечить интересную платформу для других двумерных долинных полевых транзисторов на основе материала с Y-образным искажением решетки Кекуле.
Доступность данных и материалов
Наборы данных, подтверждающие выводы этой статьи, включены в статью.
Сокращения
- AP:
-
Антипараллельный
- FM-S:
-
Ферромагнитная деформация
- Kek-Y:
-
Y-образный кекуле
- P:
-
Параллельно
- VFET:
-
Полевые транзисторы Valley
- VPMR:
-
Долина псевдомагнетосопротивления
Наноматериалы
- Решетка:MachX03D FPGA повышает безопасность за счет аппаратных возможностей корневого доверия
- Графен заменяет наноматериалы
- Графен в динамиках и наушниках
- Графеновая нанолента
- Совместно модифицированные ТИМы RGO и трехмерных графеновых сетей с высокой производительностью
- Оценка структур графен / WO3 и графен / CeO x как электродов для применения в суперконденсаторах
- Графен / полианилиновый аэрогель со сверхэластичностью и высокой емкостью в качестве высокостойкого к сжати…
- Экологичный и простой синтез нанопроволок Co3O4 и их перспективное применение с графеном в литий-ионных батаре…
- Нанокомпозиты на основе оксида графена, украшенные наночастицами серебра в качестве антибактериального аге…
- Получение нанокомпозита сверхвысокой молекулярной массы полиэтилен / графен Полимеризация на месте с помощь…



