Динамика намагничивания, модулируемая взаимодействием Дзялошинского-Мориа в магнитном туннельном переходе с двойной границей раздела спин-передача крутящего момента

Введение

Магнитная память с произвольным доступом (MRAM) является одним из наиболее многообещающих кандидатов для энергонезависимой памяти следующего поколения благодаря низкому энергопотреблению, высокой плотности, высокой скорости доступа, почти бесконечному сроку службы и хорошей совместимости с технологией CMOS [1, 2]. Элементарным устройством MRAM является магнитный туннельный переход (MTJ), который состоит из туннельного барьера, зажатого между двумя ферромагнитными слоями (называемыми закрепленным слоем и свободным слоем). Благодаря прогрессу в перпендикулярной анизотропии размер элемента MTJ был уменьшен до менее 40 нм или даже 1 × нм [3,4,5]. Тем не менее, проблема для MTJ менее 40 нм состоит в том, чтобы поддерживать адекватный барьер термической стабильности E = мк ₀ M _s H _k V / 2. (с μ ₀ магнитная проницаемость вакуума, М _s намагниченность насыщения, H _k поле анизотропии, V объем свободного слоя). Как указано в этом уравнении, E уменьшается с масштабированием MTJ, что приводит к сокращению времени хранения данных. Чтобы преодолеть эту проблему, были предложены MTJ с двойным интерфейсом для достижения достаточно высокого E на технологическом узле ниже 40 нм [6,7,8,9,10]. При использовании двух связанных ферромагнитных слоев в качестве свободного слоя композита эквивалентный объем ( V ) в двойном интерфейсе MTJ увеличен, чтобы повысить барьер термической стабильности. Между тем, постоянная демпфирования уменьшается для поддержания низкого коммутируемого тока.

В MTJ с двойным интерфейсом структура ферромагнетик / тяжелый металл (FM / HM) играет важную роль в оптимизации производительности. С одной стороны, структура FM / HM увеличивает спин-орбитальную связь (SOC), вызывая перпендикулярную анизотропию. С другой стороны, тяжелый металл работает как прокладка между двумя ферромагнитными слоями свободного слоя композита, обеспечивая взаимодействие Рудермана-Киттеля-Касуя-Йосиды (РККИ) [11], которое ферромагнитно связывает намагниченности двух ферромагнитных слоев в чтобы они вели себя как один и тот же слой. Кроме того, недавние работы демонстрируют, что сильное КПО тяжелого металла в сочетании с атомными спинами ферромагнетика может образовывать антисимметричную обменную связь, называемую взаимодействием Дзялошинского – Мориа (DMI) [12, 13]. Следовательно, DMI естественным образом индуцируется в MTJ с двойным интерфейсом со структурами FM / HM. DMI поддерживает киральные магнитные текстуры (например, спиновые спирали, скирмионы и доменные стенки неелевского типа) и существенно влияет на динамику намагничивания, что подтверждается недавними исследованиями [14,15,16,17,18,19,20,21 , 22,23,24,25]. Важно отметить, что роль DMI в двухинтерфейсном MTJ станет более сложной, так как два интерфейса FM / HM необходимо рассматривать вместе с дополнительным взаимодействием RKKY. Поэтому важно выявить влияние DMI на MTJ с двойным интерфейсом.

В этом письме мы впервые изучаем процесс переключения двухинтерфейсных MTJ под действием взаимодействия DMI и RKKY. MTJ с двойным интерфейсом переключается крутящим моментом передачи вращения (STT), который является основным подходом для записи данных в MRAM. Недавно сообщалось, что DMI пагубно влияет на переключение STT [21, 22]. Здесь наши результаты демонстрируют, что в MTJ с двойным интерфейсом отрицательное влияние DMI может быть подавлено взаимодействием RKKY, что приводит к быстрому переключению и более равномерной динамике. Наша работа доказывает устойчивость двойного интерфейса STT-MTJ к отрицательному межфазному эффекту.

Методы

Устройство, исследованное в данной работе, показано на рис. 1а со структурой FM / HM / FM в качестве свободного слоя композита. Толщина слоя HM регулируется до подходящего значения для того, чтобы индуцированное взаимодействие РККИ ферромагнитно связывало два FM-слоя. Один из FM-слоев более мягкий в магнитном отношении и обозначается как FL1 (свободный слой 1), а другой более жесткий в магнитном отношении и обозначается как FL2 (свободный слой 2). Чтобы переключить намагниченность композитного свободного слоя, ток подается на MTJ с двойным интерфейсом и генерирует STT. В этой работе мы рассматриваем только переданный STT от опорного уровня к FL1, в то время как другие моменты между FL1 и FL2 не учитываются. Эта упрощенная модель согласуется с ранее опубликованными работами [26,27,28]. DMI индуцируются как в интерфейсах FM / HM, так и в HM / FM и имеют противоположные знаки из-за разной хиральности [29].

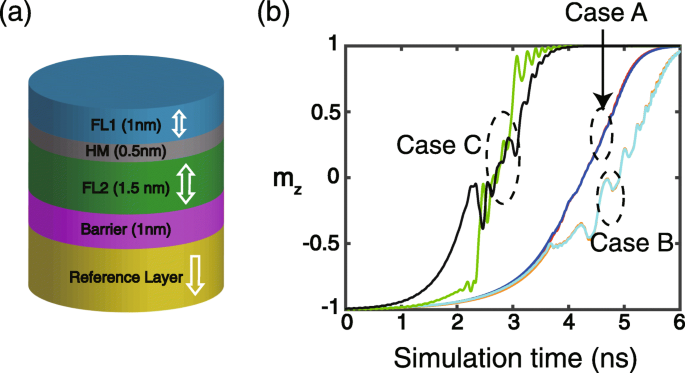
а Принципиальная схема устройства, исследуемого в данной работе. Остальные слои не показаны для ясности. б Типичные результаты зависящего от времени м _z (перпендикулярная составляющая единичной намагниченности). Случай A:σ =1 × 10 ⁻³ Дж / м ² , D ₁ = D ₂ =0 (красный для FL1, синий для FL2). Случай B:σ =1 × 10 ⁻³ Дж / м ² , D ₁ =1 мДж / м ² , D ₂ =−1 мДж / м ² (оранжевый для FL1, голубой для FL2). Случай C:σ =1 × 10 ⁻⁴ Дж / м ² , D ₁ = D ₂ =0 (зеленый для FL1, черный для FL2)

Динамика намагничивания FL1 и FL2 в MTJ с двойным интерфейсом изучается с помощью микромагнитного моделирования. Временная эволюция единичного вектора намагниченности регулируется следующим уравнением Ландау-Лифшица-Гильберта (ЛЛГ). Мы выбрали пакет OOMMF, инструмент микромагнитного моделирования с открытым исходным кодом [30], чтобы смоделировать структуру устройства и решить уравнение ЛЛГ для анализа динамики намагничивания.

где γ - гиромагнитное отношение, м - единичный вектор вдоль намагниченности, z - единичный вектор в направлении толщины, H _eff - эффективное поле, включающее одноосную перпендикулярную анизотропию, обменную энергию 6-соседей, поле DMI, взаимодействие РККИ, поле размагничивания, дипольное взаимодействие и STT. Другие параметры и их значения по умолчанию перечислены в таблице 1, если не указано иное. Эти значения параметров соответствуют новейшим технологиям. Что касается величины DMI, мы рассматриваем композитный свободный слой CoFeB / W / CoFeB в MTJ с двойным интерфейсом [10, 31,32,33]. Сообщенные экспериментальные результаты DMI для W / CoFeB варьируются от 0,12 мДж / м ² до 0,73 мДж / м ² [34,35,36]. В нашем моделировании мы расширили диапазон величины DMI до ± 2 мДж / м ² для общего исследования.

Энергия РККИ между парой магнитных моментов м _я и м _j определяется как E _ij = σ [1– м _я ∙ м _j ] / ∆ _ij , где м _я и м _j - магнитные моменты FL1 и FL2 соответственно. σ - коэффициент билинейного поверхностного обмена между двумя поверхностями. ∆ _ij размер ячейки по усмотрению в направлении от ячейки i в сторону ячейки j . В этой работе FL1 и FL2 связаны ферромагнитно, тогда σ > 0, что означает, что взаимодействие RKKY имеет тенденцию давать m _я параллельно м _j . DMI действует на соседние атомные спины S . ₁ и S ₂ через третий атом с большим SOC. Соответствующий гамильтониан DMI выражается как H _DM =- D ₁₂ ∙ ( S ₁ × S ₂ ), где D ₁₂ - вектор DMI [37]. Следовательно, DMI ухудшает однородность между S ₁ и S ₂ , который конкурирует с взаимодействием RKKY.

Результаты и обсуждение

Прежде всего, типичные результаты моделирования зависящей от времени м _z (перпендикулярная составляющая единичной намагниченности) показаны на рис. 1б. Если взаимодействие РККИ достаточно сильное (например, σ =1 × 10 ⁻³ Дж / м ² в случае A и случае B), FL1 и FL2 связаны вместе и, таким образом, их динамика намагничивания почти идентична, независимо от того, рассматривается ли DMI или нет. Также видно, что введение DMI искажает процесс переключения намагниченности (см. Случай B), что согласуется с опубликованными результатами [21,22,23] и может быть объяснено антисимметричным обменом DMI. Если взаимодействие РККИ недостаточно сильное, динамика намагничивания FL1 и FL2 не может быть идеально связана, так что между ними наблюдается значительная разница (см. Случай C). Ниже результаты моделирования получены при достаточно сильном взаимодействии RKKY, если не указано иное.

После этого мы изучаем скорость переключения при различных взаимодействиях RKKY. Скорость переключения отражается временем, когда м _z достигает 0 (определяется как время переключения). D ₁ и D ₂ установлены на положительные и отрицательные значения соответственно [29]. Соответствующие результаты показаны на рис. 2. В отсутствие DMI время переключения увеличивается с усилением взаимодействия RKKY, что согласуется с другими опубликованными результатами [26,27,28, 38]. Причина в том, что более сильное RKKY-взаимодействие делает динамику намагничивания FL1 и FL2 более когерентной, что эквивалентно увеличивает анизотропию композитного свободного слоя. Однако зависимость времени переключения от силы RKKY становится более хаотичной в присутствии DMI. Этот хаос в основном объясняется несогласованностью анизотропии между FL1 и FL2. Более подробное объяснение будет показано позже. Эти результаты свидетельствуют о немаловажном влиянии DMI на поведение переключения MTJ с двойным интерфейсом.

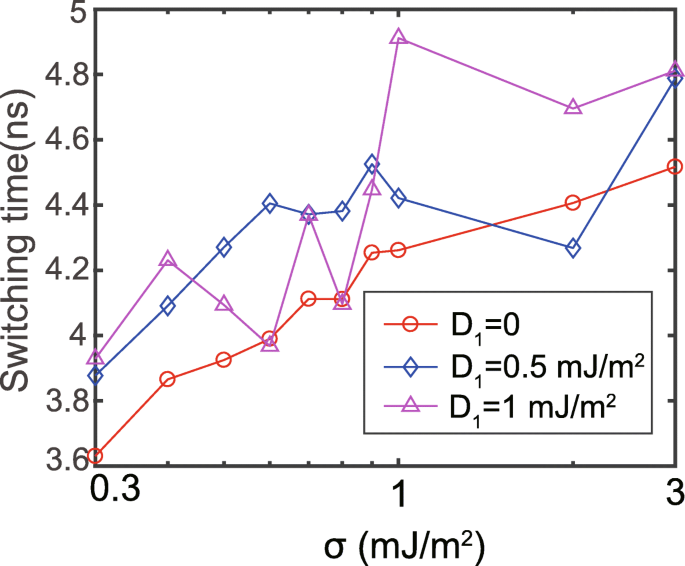
Время переключения как функция от силы RKKY, где σ отображается в логарифмической шкале. Д ₁ и D ₂ установлены те же значения, но с противоположными знаками

Далее мы более подробно изучаем влияние DMI. На рисунке 3 показано время переключения как функция мощности DMI. Важно отметить, что D ₁ и D ₂ намеренно установлены на одинаковые положительные значения на рис. 3а, хотя в действительности они имеют противоположные знаки. Другими словами, рис. 3а соответствует виртуальному случаю, который мы изучаем для проверки имитационной модели. С точки зрения физической теории вредные эффекты двух положительных ДМИ накапливаются под действием ферромагнитно связанного РККИ-взаимодействия. Поэтому ожидается, что время переключения будет увеличиваться с увеличением D . ₁ и D ₂ , как сообщалось в предыдущих работах [21, 22]. Этот анализ хорошо согласуется с результатами, показанными на рис. 3а. Таким образом подтверждается рациональность имитационной модели. В отличие от рис. 3a, вредные эффекты DMI можно было бы смягчить, если бы D ₁ и D ₂ имеют противоположные знаки, как показано на рис. 3b, где изменение времени переключения намного меньше по сравнению с рис. 3a. Обратите внимание, что на рис. 3b кривая не совсем монотонная, локальная флуктуация будет объяснена позже. Примечательно, что влияние DMI на двух интерфейсах можно было нейтрализовать, соответствующим образом настроив величины D ₁ и D ₂ , как показано на рис. 3c. Эти результаты можно объяснить с точки зрения теорий киральности следующим образом.

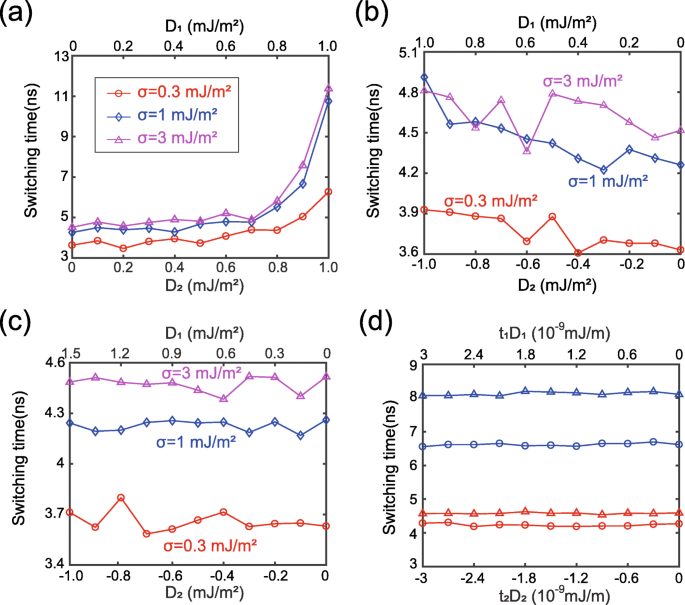
Время переключения как функция от силы DMI. а Д ₁ и D ₂ установлены на такое же положительное значение. б Д ₁ и D ₂ установлены на одно и то же значение, но с противоположными знаками. c Д ₁ и D ₂ настроены на соответствие t ₁ Д ₁ + t ₂ Д ₂ =0. d Дополнительные результаты при изменении толщины или константы анизотропии при сохранении t ₁ Д ₁ + t ₂ Д ₂ =0. синяя линия: t ₁ изменен на 2 нм; красная линия: t ₁ изменяется на 1,5 нм. Данные треугольника:σ =3 × 10 ⁻³ Дж / м ² . Данные круга:σ =1 × 10 ⁻³ Дж / м ²

Энергия DMI выражается как E _DM = t ∬ D [ м _x ( ∂m _z / ∂x ) - м _z ( ∂m _x / ∂x ) + м _y ( ∂m _z / ∂y ) - м _z ( ∂m _y / ∂y )] d ² г = tDε _DM [39], где D - непрерывная постоянная DMI, t - толщина ферромагнитного слоя. Как упоминалось выше, динамика намагниченности FL1 и FL2 практически идентична при достаточно сильном взаимодействии РККИ. В этом случае то же ε _DM получается в FL1 и FL2. Тогда полная энергия DMI FL1 и FL2 может быть рассчитана с помощью E _тот =( t ₁ Д ₁ + t ₂ Д ₂ ) ε _DM . Следовательно, установив D ₁ / D ₂ =- t ₂ / t ₁ , эффекты DMI FL1 и FL2 могут быть полностью компенсированы в случае достаточно большого σ, что согласуется с рис. 3c. Этот вывод дополнительно подтверждается дополнительными результатами, показанными на рис. 3d, где другие параметры намеренно изменяются при сохранении D ₁ / D ₂ =- t ₂ / t ₁ .

Эквивалентная величина DMI ( D _eq ) составного свободного слоя можно выразить как D _eq =( t ₁ Д ₁ + t ₂ Д ₂ ) / ( t ₁ + t ₂ ), который можно использовать для количественного анализа влияния DMI на MTJ с двойным интерфейсом. Чтобы проверить эффективность этого уравнения, мы показываем две группы результатов моделирования на рис. 4a, где две кривые были получены при одном и том же D _eq но с двумя парами разных { D ₁ , D ₂ } значения соответственно. Хотя между двумя кривыми есть небольшая разница, их общие тенденции схожи и подтверждают пагубное влияние DMI на переключение STT. Здесь разницу между двумя кривыми можно объяснить следующим образом. FL1 и FL2 имеют разные константы анизотропии, что приводит к локальным неопределенным колебаниям динамики намагниченности, как показано на рис. 4c. То же явление наблюдается и на рис. 2 и рис. 3б. Вместо этого на рис. 4b, d показан идеальный случай, где константы анизотропии FL1 и FL2 установлены на одинаковые значения. Ясно, что видно хорошее совпадение двух кривых, что указывает на то, что приведенное выше выражение D _eq вполне может описать эквивалентный эффект DMI двойного интерфейса MTJ.

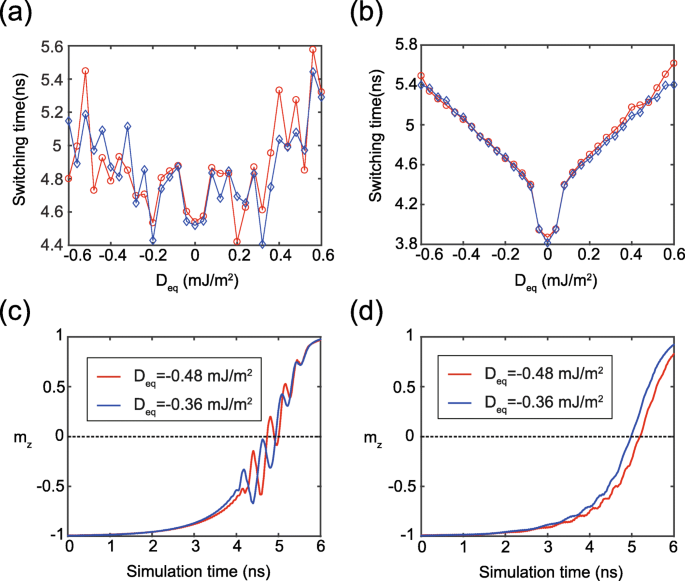
а , b Время переключения как функция от D _eq . Каждый D _eq получается с двумя парами разных { D ₁ , D ₂ } значения согласно D _eq =( t ₁ Д ₁ + t ₂ Д ₂ ) / ( t ₁ + t ₂ ). Красная кривая: D ₁ между тем меняется D ₂ фиксируется на уровне 1 мДж / м ² . Синяя кривая: D ₁ и D ₂ всегда имеют одно и то же значение. Здесь σ =1 × 10 ⁻² Дж / м ² . В а , остальные параметры сконфигурированы как таблица 1. В b , К _{u 1} = К _{u 2} =0,7 мДж / м ³ для идеального случая. c , d Типичные результаты зависящих от времени м _z соответствует a и b соответственно

Наконец, мы более подробно анализируем временную эволюцию динамики намагниченности. На рис. 5 показана зависящая от времени энергия при переключении намагничивания. Энергии DMI FL1 и FL2 накапливаются или аннулируются, в зависимости от знаков и величин D ₁ и D ₂ . Эта тенденция хорошо согласуется с приведенными выше теоретическими моделями. Кроме того, энергии RKKY поддерживаются на низких значениях, что подтверждает синхронное управление магнитными моментами FL1 и FL2. Распределение полей RKKY и DMI показано на рис. 6, где поле RKKY играет разные роли в разных случаях. Во-первых, в случае ненулевого DMI (см. Случай 2 и случай 3) поле RKKY намного сильнее по сравнению со случаем нулевого DMI (см. Случай 1). Можно понять, что поле RKKY должно преодолевать дополнительную неоднородность магнитных текстур в присутствии DMI. Во-вторых, если D ₁ и D ₂ имеют противоположные знаки, поле RKKY противостоит полям DMI как в FL1, так и в FL2 (см. случай 2). В результате DMI ослабляется, так что динамика намагничивания становится более однородной. Напротив, когда-то D ₁ и D ₂ имеют тот же знак, поле RKKY противостоит полю DMI в одном ферромагнитном слое, но помогает ему в другом ферромагнитном слое (см. случай 3). Таким образом, общее поле DMI по-прежнему оказывает определенное влияние на динамику намагничивания, что подтверждает, что DMI не может быть отменен, если D ₁ и D ₂ одного знака.

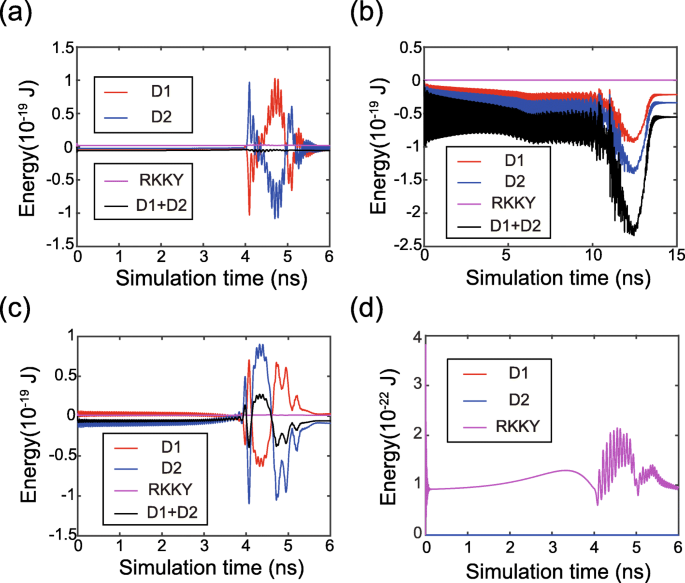
Временная эволюция энергий DMI и RKKY. а Д ₁ =1,5 мДж / м ² , D ₂ =- 1 мДж / м ² , т.е. эффект DMI отменяется. б Д ₁ = D ₂ =1 мДж / м ² , т.е. эффект DMI накапливается. c Д ₁ =1 мДж / м ² , D ₂ =- 1 мДж / м ² , т.е. эффект DMI смягчается, но не отменяется. г Д ₁ = D ₂ =0

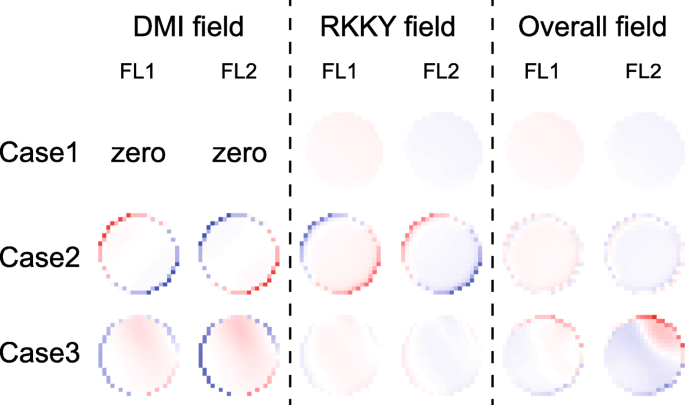
Пространственные распределения полей DMI и RKKY. Здесь показан типичный результат в один момент времени для каждого случая. В остальные моменты времени вывод остается неизменным. Случай 1: D ₁ = D ₂ =0. Случай 2: D ₁ =1,5 мДж / м ² , D ₂ =- 1 мДж / м ² , т.е. эффект DMI отменяется. Случай 3: D ₁ = D ₂ =1 мДж / м ² , т.е. эффект DMI накапливается

На рисунке 7 показаны микромагнитные конфигурации FL1 и FL2 во время переключения намагниченности. Хотя доменная стенка появляется во всех случаях, в некоторые моменты времени могут наблюдаться разные особенности. Хорошо известно, что DMI способствует неоднородным магнитным текстурам. Тем не менее, на рис. 7 однородная намагниченность все еще формируется даже в присутствии DMI (см. Время, когда m _z =- 0,5 в случае 2), пока эффект DMI отменен. Опять же, этот результат подтверждает приведенную выше теоретическую модель. Кроме того, также видно, что динамика намагничивания более неоднородна, если D ₁ и D ₂ имеют один и тот же знак (см. случай 3, где всегда появляется доменная стенка), что согласуется с приведенным выше анализом. Мы также показываем некоторые результаты, смоделированные с меньшим MTJ (см. Последние две строки на рис. 7). Разница микромагнитных конфигураций между случаем 2 (DMI отменяется) и случаем 3 (DMI не отменяется) более заметна.

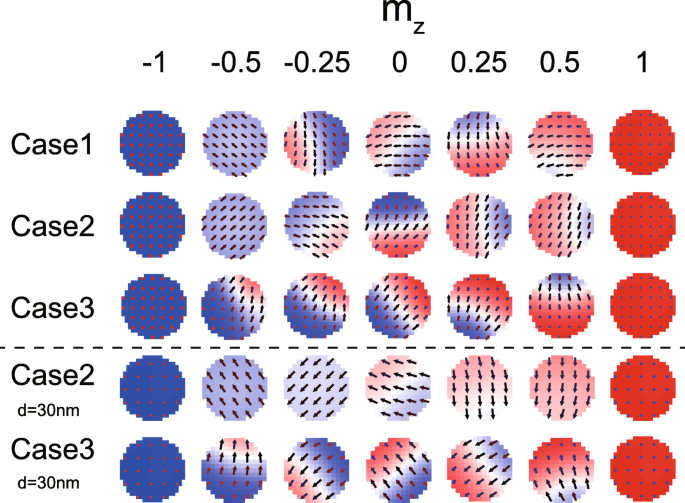
Микромагнитные конфигурации при переключении намагниченности. Здесь варианты 1–3 настроены с теми же параметрами, что и на рис. 6

Заключение

Мы всесторонне изучили влияние DMI на STT-MTJ с двойным интерфейсом. Как известно, MTJ с двойным интерфейсом был разработан для повышения барьера термостойкости. В этой работе наши результаты подтверждают еще одно преимущество MTJ с двойным интерфейсом, то есть подавление вредного воздействия DMI. DMI в двух ферромагнитных слоях могут быть подавлены или даже отменены, если они настроены с соответствующими значениями и противоположными знаками, что, естественно, удовлетворяется структурой STT-MTJ с двойным интерфейсом. Для объяснения вывода были предложены теоретические модели. Обсуждались результаты микромагнитного моделирования для выявления роли DMI в динамике намагничивания. Наша работа обеспечивает реальный подход к минимизации DMI в двойном интерфейсе STT-MTJ.

Доступность данных и материалов

Все данные полностью доступны без ограничений.

Сокращения

DMI:

Взаимодействие Дзялошинского – Мория

FL:

Свободный слой

FM / HM:

Ферромагнетик / тяжелый металл

MRAM:

Магнитная оперативная память

MTJ:

Магнитный туннельный переход

RKKY:

Рудерман – Киттель – Касуя – Йосида

SOC:

Спин-орбитальная связь

STT:

Крутящий момент передачи вращения