Одновременное создание нескольких трехмерных кривых луча трактора

Введение

Давным-давно люди продемонстрировали способность света проявлять силу. Идея привлекать объекты с помощью оптических лучей тоже долгое время привлекала наше внимание. Из-за фазовой сингулярности и уникального орбитального углового момента оптический вихрь имеет важное исследовательское значение в области оптических микроманипуляций, квантовой связи, визуализации оптических изображений и оптических измерений [1,2,3,4,5,6]. Хотя технология создания оптических вихрей была разработана и может быть полезна в различных приложениях, эффективность одного оптического вихря все еще невысока. Для одновременного захвата нескольких частиц и раздельной обработки различных частиц создание массивов оптических вихрей стало актуальной темой [7, 8].

Недавние теоретические исследования [9,10,11,12,13] показали, что притягивающий луч представляет собой бегущую волну, которая может транспортировать освещенный материал по своей длине обратно к источнику. Новые достижения в управлении лазерным лучом привели к экспериментальной реализации тяговых лучей [14, 15]. Одним из важных типов трехмерных вихревых ловушек является так называемый соленоидный луч, который имеет фиксированную спиральную форму вокруг оптической оси [16], в которой можно задать градиент фазы вдоль этой кривой для получения притягивающего луча. Это было достигнуто путем наложения спиральных фаз на коллинеарную суперпозицию бесселевых пучков. Раффнер и Гриер [17] экспериментально продемонстрировали и проанализировали свойства класса притягивающего луча, полученного интерференцией двух коаксиальных Бесселевых лучей, различающихся по своим осевым волновым числам. В 2013 году Родриго и др. представить метод эффективной генерации тяговых лучей путем загрузки спроектированных фазовых голограмм в пространственный модулятор света (ПМС) и одновременного облучения ПМС лазерами. Они использовали эту технику, позволяющую генерировать градиентные пучки высокой интенсивности (HIG), фаза и интенсивность которых задаются на основе компьютерной голограммы (CGH) [18]. Они экспериментально доказали, что балкам в различных трехмерных геометриях можно придать форму. HIG и силы фазового градиента имеют решающее значение для создания трехмерных лазерных ловушек, которые способны перемещать множество частиц даже против давления светового излучения [19]. Родриго также показал, что лазерная ловушка для фристайла, включая силы HIG и градиент фазы, может удерживать несколько частиц и управлять их движением [20]. Однако большая часть представленных работ сосредоточена на создании простых трехмерных тяговых лучей, что имеет ограничения в дальнейшем развитии приложений формирования луча. Основываясь на приведенном выше анализе, срочно необходима усовершенствованная технология формирования луча для создания нескольких трехмерных тяговых лучей.

В этой статье мы демонстрируем метод генерации нескольких трехмерных притягивающих лучей с использованием модифицированной техники голографического формирования луча, где все CGH мультиплексируются и кодируются в одну фазовую голограмму путем добавления соответствующей линейной фазовой решетки. Мы проектируем несколько трехмерных тяговых балок, скрученных под разными углами. Ожидается, что такие> новые притягивающие лучи расширят область применения оптических вихрей и потенциально могут быть полезны при реализации сверхэффективных множественных оптических приложений.

Методы

На рис. 1а показана схема методики голографического трехмерного формирования пучка из [18], которая позволяет проектировать сложные пучки, интенсивность и фазовое распределение которых соответствуют заданной трехмерной кривой. Кодирование поля комплексной амплитуды в фазовые голографические решетки - это метод расчета CGH. В частности, чтобы создать желаемый фокусный луч, комплексная амплитуда падающей плоскости задается выражением:

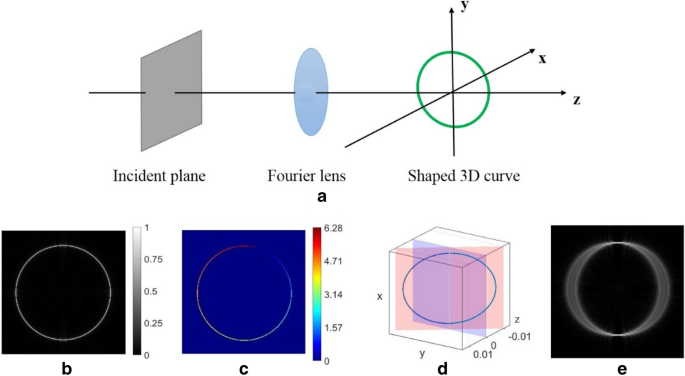
а Схема техники формирования голографического 3D-луча. б , c Восстановленное распределение интенсивности и фазы 2D кольцевой кривой в фокальной плоскости. г Пространственная схема кольцевой кривой, наклоненной относительно плоскости z =0. e Кольцевой притягивающий луч сфокусирован в фокальной плоскости ( z =0)

Условия ψ ( x , y , t ) и φ ( x , y , t ) в уравнении. (1) определяются

[ x ₀ ( т ), y ₀ ( т ), z ₀ ( т )] представляет заданную трехмерную кривую в декартовой координате с t ∈ [0,2 π ]. е ₀ и λ относятся к фокусному расстоянию линзы Фурье и длине волны соответственно.

Уравнение Уравнение (1) позволяет рассчитать падающее комплексное поле (а именно сложный CGH), которое может формировать структурно устойчивый фокусный луч со специальным распределением интенсивности и градиентом фазы (спиральная фаза вдоль кривой). Сначала рассмотрим двумерную кольцевую кривую x ₀ ( т ) =Rcos ( t ), y ₀ ( т ) =Rsin ( t ). Распределение интенсивности полученного луча показано на рис. 1б. Фазовое распределение кольца хорошо определено вдоль кривых под топологическим зарядом m =1 (см. Рис. 1в). Рассмотрим наклонное кольцо на рис. 1г. Плоскость кольцевой кривой наклонена на определенный угол на основе плоскости z =0. В этом случае луч фокусируется, появляясь в верхней и нижней точках [см. Рис. 1e].

Чтобы мультиплексировать лучи различных кривых трактора, частично разделенные в фокусном поле, каждый комплексный CGH, рассчитанный по формуле. (1) должен быть закодирован с уникальной несущей частотой. Этого можно добиться, добавив на голограмму каждого луча линейную фазовую решетку. Линейные решетки в сочетании с пространственными фильтрами обычно используются для отделения первого порядка дифракции от нежелательных нулевых и более высоких порядков дифракции. Передаточная функция линейной фазовой решетки задается как

u _я и v _я - пространственные координаты генерируемого луча в дальней зоне, полученные с помощью линзы Фурье с фокусным расстоянием f ₀ . к =2 π / λ - волновое число, а z _я представляет собой осевое смещение от фокальной плоскости (плоскости Фурье). Для одновременного создания лучей кривой тяги, выражения окончательного сложного CGH должны быть добавлены

Результаты и обсуждение

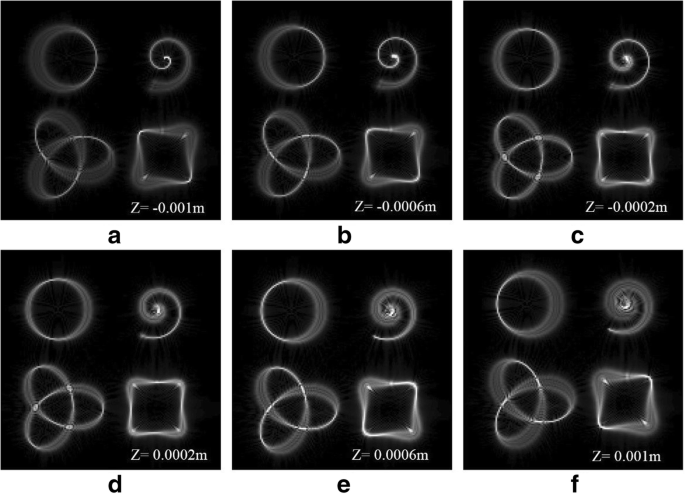
Регулирование светового поля в 3D-конфигурации очень важно в практических приложениях, таких как 3D-манипуляции с частицами в жидкой среде. Поэтому мы изучаем генерацию пучков HIG, интенсивность и фаза которых задаются вдоль трехмерных кривых разной формы. В частности, мы рассматриваем наклонное кольцо на рис. 2a – e, архимедову спираль на рис. 2f – j, кривую с узлами трилистника на рис. 2k – o и квадратную кривую на рис. 2p – t. Соответствующие выражения кривых представлены в таблице 1. Эти трехмерные структуры выявляются по ходу распространения луча в фокальной области. Распределение интенсивности луча, измеренное в фокальной плоскости ( z =0) показаны в третьем столбце рис. 2. Знаки Z координаты, соответствующие другим столбцам на рис. 2, отмечены на схемах моделирования.

Результаты моделирования 3D тяговых лучей . а - е Кольцевая кривая трехмерных тяговых лучей, сфокусированных на разных z самолеты. е - j Архимедова спираль трехмерных тяговых лучей, ориентированных на разные z самолеты. к - o Трилистниковая кривая трехмерных тяговых лучей, сфокусированных на разных z самолеты. р - т Квадратная кривая трехмерных тяговых лучей, сфокусированных на разных z самолеты

В области оптических микроманипуляций тяговые лучи с разной степенью трехмерного искажения могут играть большую роль в приложениях. Однако для повышения эффективности крайне желательно синхронно выполнять дифференцированные манипуляции в разных местах. Таким образом, мы проектируем несколько притягивающих лучей из четырех шаблонов одновременно, каждый из которых может использоваться для удержания заданных частиц в любой заданной геометрической кривой с определенной степенью трехмерного искажения. Взаимное расположение тяговых лучей можно спроектировать. Чтобы показать, что несколько притягивающих лучей сфокусированы на трехмерной области, мы выбрали шесть двухмерных плоскостей для наблюдения. Притягивающие лучи фокусируются в различных 2D-плоскостях, как показано на рис. 3. Эти 3D-структуры выявляются по мере распространения луча в фокальной области.

Результаты моделирования нескольких трехмерных тяговых лучей в разных местах. а - c Восстановленная интенсивность лучей перед фокальной плоскостью. г - е Восстановленная интенсивность лучей после фокальной плоскости

Чтобы наблюдать взаимодействие множества управляемых частиц, мы разработали медноподобные вложенные графические тяговые лучи. 3D-искажения и формы внутренних и внешних балок могут быть разработаны отдельно. Кривая кольца сфокусирована на плоскости ( z =0), а квадратная кривая имеет определенную степень трехмерного искажения (см. Рис. 4a – e). Квадратная кривая сфокусирована на плоскости ( z =0), а кольцевая кривая имеет определенную степень трехмерного искажения (см. Рис. 4f – j). Распределение интенсивности луча, измеренное в фокальной плоскости ( z =0) показаны в третьем столбце рис. 4. Значки z координаты, соответствующие другим столбцам на рис. 4, отмечены на диаграммах моделирования. Форму тяговых лучей можно гибко регулировать для управления частицами в различных положениях.

Результаты моделирования медноподобных вложенных графических тяговых балок. а - е Лучи в форме наклонной квадратной кривой фокусируются на разных z самолеты. е - j Лучи, имеющие форму наклонного кольца, фокусируются на разных z самолеты

Были проведены оптические эксперименты, чтобы убедиться, что представленный выше метод может быть использован для достижения цели фокусировки нескольких трехмерных притягивающих лучей в настраиваемых областях фокусировки. Как показано на рис. 5, оптическая установка для создания трехмерного притягивающего луча состоит из жидкокристаллического пространственного модулятора света (SLM), системы фильтрации 4f и линзы с преобразованием Фурье (фокусирующей). Твердотельный лазер с длиной волны 532 нм коллимирован для освещения плоскими волнами. SLM (Holoeye Pluto, шаг 8 пикселей, разрешение 1920 × 1080) используется для адресации только фазового CGH. Мы используем двухфазный метод [18, 20] для кодирования комплексного CGH H ( x , y ) рассчитывается по формуле. (4) в фазовый CGH. Он заключается в кодировании сложной функции в виде голограммы в SLM. Луч, модулированный SLM, затем проецируется на заднюю апертуру линзы с преобразованием Фурье ( f =400 мм) через конфигурацию оптической фильтрации 4f. Камера устройства с зарядовой связью (CCD) помещается в плоскости Фурье фокусирующей линзы для записи сгенерированных диаграмм интенсивности. Результаты трехмерных притягивающих лучей показаны на рис. 6. Хотя полученные лучи имеют ошибки после прохождения через оптическую систему 4f, они хорошо согласуются с результатами моделирования.

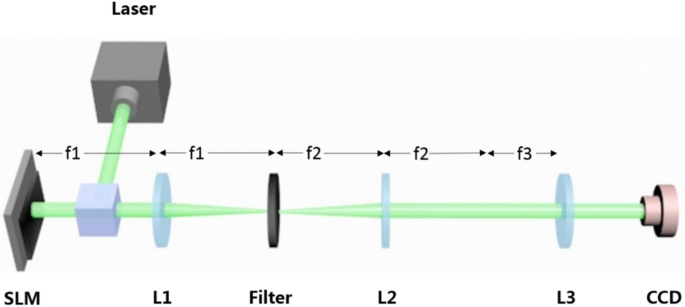
Экспериментальная установка. Голограмма адресуется в ПМС, который освещается коллимированным лазерным лучом. После прохождения луча через линзу 1 желаемый рисунок может быть отфильтрован с помощью диафрагмы. Затем полученные лучи проходят через объектив 2 и объектив 3 и могут быть захвачены камерой

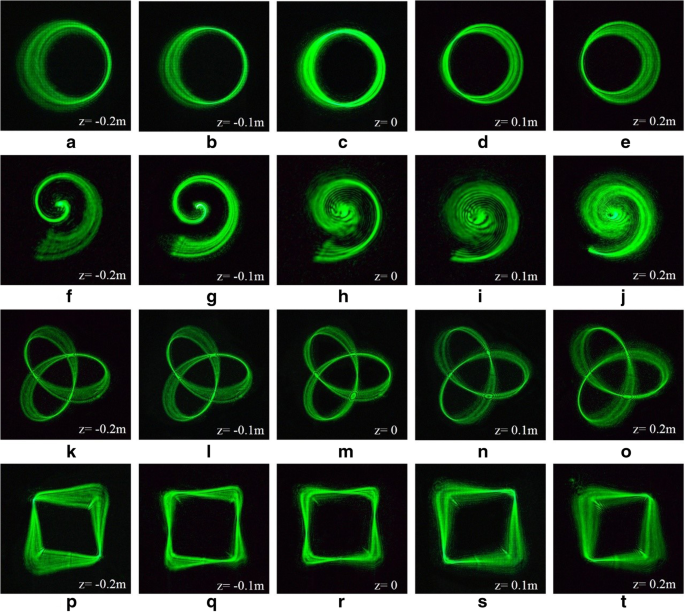
Экспериментальные результаты 3D тяговых лучей. а - е Кольцевая кривая трехмерных тяговых лучей, сфокусированных на разных z самолеты. е - j Архимедова спираль трехмерных тяговых лучей, ориентированных на разные z самолеты. к - o Трилистниковая кривая трехмерных тяговых лучей, сфокусированных на разных z самолеты. р - т Квадратная кривая трехмерных тяговых лучей, сфокусированных на разных z самолеты

Результаты нескольких трехмерных тяговых лучей показаны на рис. 7. Мы выбрали шесть двухмерных плоскостей для наблюдения, что удобно для сравнения с моделированием. Результаты моделирования хорошо согласуются с результатами экспериментов. Подтверждено, что этот метод может гибко и эффективно генерировать несколько трехмерных тяговых лучей. Различные лучи с определенной степенью трехмерного искажения могут удерживать частицы.

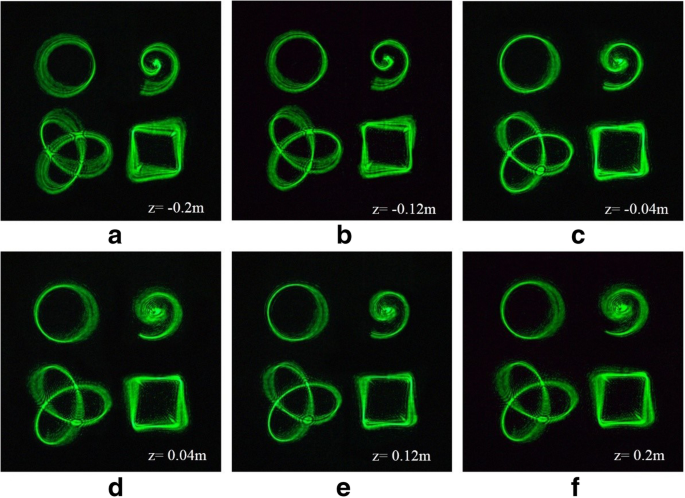
Экспериментальные результаты нескольких трехмерных тяговых лучей в разных местах. а - c Восстановленная интенсивность лучей перед фокальной плоскостью. г - е Восстановленная интенсивность лучей после фокальной плоскости

Результаты медеподобных вложенных графических тяговых лучей показаны на рис. 8. Результаты моделирования хорошо согласуются с экспериментальными результатами. Таким образом, две вложенные балки практически не взаимодействуют друг с другом. Тяговые лучи можно использовать для манипулирования множеством частиц на разных кривых.

Экспериментальные результаты медеподобных вложенных графических тяговых лучей. а - е Лучи в форме наклонной квадратной кривой фокусируются на разных z самолеты. е - j Лучи, имеющие форму наклонного кольца, фокусируются на разных z самолеты

Заключение

Мы проектируем несколько трехмерных тяговых балок, пространственное расположение которых регулируется независимо. Между тем, каждая отдельная балка могла быть прописана вдоль произвольных геометрических кривых и закручена под произвольными углами по желанию. Мы теоретически и экспериментально доказываем, что создание оптических тяговых лучей в трехмерной конфигурации может быть легко достигнуто. Градиенты высокой интенсивности и фазовые градиенты могут захватывать частицы. В настоящее время проведены эксперименты, и оптические вихревые пучки повреждают частицы до минимальной степени. Наша работа расширяет ассортимент тяговых балок. Считается важным и полезным для дальнейшего развития тяговых лучей для различных оптических приложений.

Сокращения

2D:

Двумерный

3D:

Трехмерный

CGH:

Компьютерная голограмма

HIG:

Градиент высокой интенсивности

SLM:

Пространственный модулятор света