Управляемая оптическая бистабильность и четырехволновое смешение в оптомеханике фотонных молекул

Фон

Оптомеханические системы (OMS) [1], состоящие из оптических резонаторов, соединенных с механическими резонаторами и исследующие индуцированные радиационным давлением когерентные фотон-фононные взаимодействия, в последнее время привлекли большое внимание, поскольку они предлагают платформу для управления механическими резонаторами и электромагнитными полями и прокладывают путь путь для потенциальных применений оптомеханических устройств, таких как фононный лазер [2, 3], зондирование [4], сжатие фононов [5], реализация сжатого света [6–8], охлаждение основного состояния [9–11], и оптико-механически индуцированная прозрачность (OMIT) [12–15] -индуцированная запаса света в твердотельных устройствах [16, 17]. Хотя наибольшее внимание было уделено одиночному OMS, для реализации составного OMS путем интеграции большего количества оптических или механических мод, таких как одна механическая мода, связанная с двумя оптическими модами, посредством давления излучения [18, 19] и фононного взаимодействия между двумя механическими резонаторами [20 , 21] становятся тенденцией для дальнейшего исследования OMS и их потенциальных приложений в квантовой обработке информации. На основе гибридного соединения OMS широко исследуются перенос квантового состояния [22], OMIT-подобное фононное охлаждение [23], оптомеханическая темная мода [24] и фононно-опосредованное электромагнитно-индуцированное поглощение [25]. В многочисленных составных OMS, как естественном расширении общего OMS, большое внимание привлекли две непосредственно связанные микрополости моды шепчущей галереи (WGM), называемые фотонными молекулами [26, 27] с оптомеханическим эффектом в одной WGM. В составной оптико-механической системе фотонных молекул существует два вида взаимодействия:первый - это оптомеханическое взаимодействие, индуцированное давлением излучения, а второй - взаимодействие резонатора с резонатором посредством настраиваемого туннелирования фотонов. Эти два взаимодействия вместе вызывают несколько интересных явлений, включая генерацию фононов [2, 3], хаос [28], охлаждение основного состояния [23] и когерентное управление светопропусканием [25, 29, 30].

С другой стороны, OMS также предоставляет платформу для исследования нелинейного эффекта взаимодействия света и вещества. Среди всех нелинейных явлений в OMS, оптическая бистабильность и четырехволновое смешение (FWM) являются типичными нелинейно-оптическими явлениями, привлекающими интерес исследователей. В последнее время бистабильное поведение среднего числа внутрирезонаторных фотонов интенсивно изучалось в различных ОМС, таких как оптомеханическая система с конденсатным резонатором Бозе-Эйнштейна [31, 32], ОМС с квантовой ямой [33], ультрахолодные атомы [34, 10]. 35] и других гибридных ОМС [36, 37]. Кроме того, FWM можно описать как резонатор, управляемый мощным лазером накачки с частотой ω _p и частота слабого зондирующего лазера ω _s , а затем два фотона накачки будут смешиваться с пробным фотоном через механический режим, давая холостой фотон с частотой 2 ω _p - ω _s в OMS, и это также исследовалось в предыдущих работах, таких как расщепление мод в оптомеханической системе с сильной связью [38], OMS с когерентным механическим возбуждением [39, 40] и двухмодовой оптомеханической системе резонатора [41]. Однако оптическая бистабильность и FWM редко изучались в композитных фотонно-молекулярных OMS, где сила связи, представленная как J двух резонаторов играют ключевую роль в этих нелинейных оптических явлениях.

В настоящей работе мы рассматриваем составную оптомеханическую систему резонатора фотонно-молекулярного резонатора, состоящую из двух микрополостей МШГ, где один резонатор МШГ представляет собой оптомеханический резонатор с высокой диссипацией резонатора κ , а другой резонатор МШГ является обычным вспомогательным оптическим резонатором с добротностью (Q) [42]. Как Лю и др. [43] продемонстрировали, что по-прежнему трудно достичь высокой добротности и малого объема моды (V) одновременно для одного и того же типа резонатора. В оптомеханике фотонных молекул путем соединения изначально оптико-механической полости c с высокой диссипацией резонатора κ (без высокой добротности) в режим вспомогательного резонатора a с высокой добротностью, но с большим V, требование высокой добротности и малого V для одного и того же резонатора может быть устранено. Введем коэффициент отношения δ = κ _c / κ _а , где κ _c = ω _c / Q _c и κ _а = ω _а / Q _а - скорости затухания мод резонатора c и a ( ω _c и ω _а - частоты резонатора c и a ) для исследования нелинейных эффектов в оптомеханике фотонных молекул. Здесь оптомеханический резонатор c управляется лазером накачки, а вспомогательный резонатор a управляется зондирующим лазером. Полость c соединен с полостью a через исчезающее поле, а сила связи J между двумя полостями можно контролировать, изменяя расстояние между двумя полостями WGM [26]. Мы исследуем оптическую бистабильность и FWM на основе композитного фотонно-молекулярного OMS путем изменения силы связи J между объемными резонаторами, а настраиваемая и управляемая оптическая бистабильность и FWM могут быть достигнуты путем изменения силы связи J между двумя полостями. Далее, регулируя параметр δ и мощность насоса P , процессом FWM можно управлять.

Модель и теория

Оптомеханика фотонных молекул показана на рис. 1. Первый резонатор поддерживает оптическую моду c с частотой ω _c управляемый лазером накачки с частотой ω _p и амплитуда \ (\ varepsilon _ {p} =\ sqrt {P / \ hbar \ omega _ {p}} \). Радиационное давление вызывает механический режим b с частотой механического резонатора ω _м , а скорость однофотонной оптомеханической связи составляет g = г ₀ x ₀ ( г ₀ = ω _c / R и R - радиус полости c ), а нулевое колебание положения механического осциллятора равно \ (x_ {0} =\ sqrt {\ hbar / 2M \ omega _ {m}} \) [13]. Тогда гамильтониан оптомеханики c это [13]

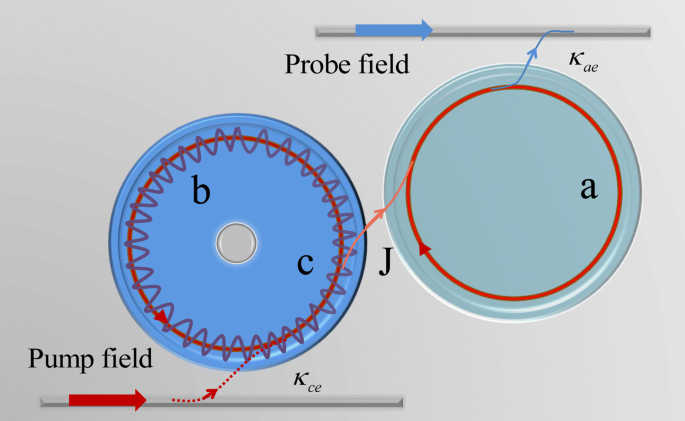
Принципиальная схема композитной оптомеханической системы фотонно-молекулярного резонатора, включающего два резонатора МШГ. Первый резонатор WGM с высокой диссипацией резонатора κ оптомеханический резонатор c возбуждается лазером накачки, а сила давления излучения вызывает механическую моду b соединение с полостью c с силой сцепления г . Вторая полость WGM a представляет собой вспомогательный резонатор, управляемый пробным лазером с высокой добротностью (Q). Оптомеханическая полость c соединен с полостью a через кратковременное поле, и мы вводим параметр J для описания силы связи двух полостей, которой можно управлять, варьируя расстояние между ними [26]

где Δ _c = ω _c - ω _p - расстройка поля накачки и резонатора c . c и c ^† представляют собой операторы бозонной аннигиляции и создания резонатора моды c , и b ^† ( b ) - оператор создания (уничтожения) механического режима. Вспомогательный резонатор поддерживает только оптический режим a управляемый зондирующим лазером с частотой ω _s , а его амплитуда ε _s это \ (\ varepsilon _ {s} =\ sqrt {P_ {s} / \ hbar \ omega _ {s}} \). Мы вводим операторы уничтожения и создания a и a ^† для описания полости a , а его гамильтониан равен [13]

где Δ _а = ω _а - ω _p - расстройка поля накачки и резонатора a , и Ω = ω _s - ω _p - расстройка насос-зонд. Мы используем два сужающихся волокна для возбуждения моды резонатора a и режим резонатора c как оптический волновод со скоростью связи κ _а.е. и κ _ce . Оптомеханическая полость c пары в полость a через затухающее поле, а коэффициент связи резонатор-резонатор Дж можно эффективно настраивать, изменяя расстояние между ними [26]. Когда сила сцепления J слабая между двумя полостями, то энергия из полости c не может легко попасть в полость a . И наоборот, если прочность связи J увеличивается с уменьшением расстояния между двумя полостями, тогда энергия может легко течь из двух полостей. Линейно связанное взаимодействие между двумя полостями описывается формулой [26] \ (\ hbar J \ left (a ^ {\ dag} c + ac ^ {\ dag} \ right) \). Тогда полный гамильтониан во вращающейся волновой системе с частотой накачки ω _c можно записать [3, 13, 23]

Скорость затухания двух резонаторов моды κ = κ _c = κ _а = κ _бывший + κ ₀ с собственной скоростью потери фотонов κ ₀ , и κ _бывший описывает скорость, с которой энергия покидает оптический резонатор в распространяющиеся поля [13]. Здесь для простоты мы рассматриваем только условие κ _бывший = κ ₀ = κ _а.е. = κ _ce , и мы рассматриваем ω _c = ω _а .

Мы используем уравнение движения Гейзенберга \ (i \ hbar \ partial _ {t} O =[O, H] \) ( O = а , c , X ) и введем соответствующие операторы затухания и шума, и мы получим квантовые уравнения Ланжевена следующим образом [44]:

где X = b ^† + b - оператор позиции, а γ _м - скорость распада резонатора. а _в и c _в описывающие шумы Ланжевена следуют соотношениям [45]

На режим резонатора влияет стохастический силовой процесс со следующей корреляционной функцией [46]

где k _B - постоянная Больцмана и T указывает температуру пласта.

Когда оптомеханическая полость c управляется мощным лазером накачки, оператор Гейзенберга можно разделить на две части, т.е. установившееся среднее значение O ₀ , и небольшое колебание δ О с нулевым средним значением 〈 δ О 〉 =0. Установившиеся значения определяют количество фотонов внутри резонатора ( n _а =| а _s | ² и н _c =| c _s | ² ) определяется

где \ (\ Delta ^ {^ {\ prime}} =\ Delta _ {c} -2g ^ {2} n_ {c} / \ omega _ {m} \). Такая форма связанных уравнений характерна для оптической бистабильности. В следующем разделе мы обсудим такие параметры, как мощность накачки P , сила связи резонатор-резонатор J , а параметр отношения δ которые влияют на оптическую бистабильность. Сохраняя только линейные члены флуктуационных операторов и составляя анзац [47] 〈 δ а 〉 = а ₊ е ^{- я Ом т} + а _- е ^{я Ом т} , 〈 δ c 〉 = c ₊ е ^{- я Ом т} + c _- е ^{я Ом т} , 〈 δ X 〉 = X ₊ е ^{- я Ом т} + X _- е ^{я Ом т} , тогда получаем

где \ (\ Lambda _ {1} =igc_ {s} ^ {2} \ eta ^ {\ ast} J ^ {2} \ varepsilon _ {s} \ sqrt {\ kappa _ {ae}} \), <я> Λ ₂ =( я Δ _{а 2} + κ _а ) ( я Δ ₂ + κ _c ) [( я Δ ₁ - κ _c ) ( я Δ _{а 1} - κ _а ) - Дж ² ], \ (\ Lambda _ {3} =- g ^ {2} \ eta ^ {\ ast 2} n_ {c} ^ {2} (i \ Delta _ {a1} - \ kappa _ {a}) ( i \ Delta _ {a2} + \ kappa _ {a}) \), Δ _{а 1} = Δ _а - Ом , Δ _{а 2} = Δ _а + Ом , \ (\ Delta _ {1} =\ Delta ^ {^ {\ prime}} - \ Omega + g \ eta n_ {c} \), \ (\ Delta _ {2} =\ Delta ^ {^ {\ prime}} + \ Omega + g \ eta ^ {\ ast} n_ {c} \) и \ (\ eta =2g \ omega _ {m} / (\ omega _ {m} ^ {2} -i \ гамма _ {m} \ Omega - \ Omega ^ {2}) \). Используя стандартное соотношение ввода-вывода [45] \ (a _ {\ text {out}} (t) =a _ {\ text {in}} (t) - \ sqrt {2 \ kappa _ {a}} a (t ) \), где a _вне ( т ) является оператором выходного поля и получает ожидаемое значение выходных полей:

где a _вне ( т ) - оператор выходного поля. Уравнение (13) показывает, что поле вывода состоит из трех членов. Первый член соответствует выходному полю в управляющем поле с амплитудой ε _p и частота ω _p . Второе слагаемое соответствует пробному полю с частотой ω _s связанное с антистоксовым полем, приводящим к ОМИТ, которое исследовалось в различных оптомеханических системах [12–15, 48]. Последний соответствует выходному полю с частотой 2 ω _p - ω _s связанные со стоком, поле отображения FWM. В процессе FWM два фотона управляющего поля взаимодействуют с одним фотоном зондирующего поля, каждый с частотами ω _p и ω _s родился новый фотон с частотой 2 ω _p - ω _s . Интенсивность FWM в терминах пробного поля может быть определена как [49]

которая определяется оптомеханической прочностью связи g , мощность насоса P , сила связи резонатор-резонатор J , а отношение скоростей распада δ из двух полостей.

Числовые результаты и обсуждения

В этом разделе мы сначала исследуем бистабильное поведение стационарного числа фотонов n _c и н _а двух полостей в соответствии с уравнениями. (10) и (11). Поскольку дать аналитическое выражение условия бистабильности слишком громоздко, здесь мы приведем численные результаты. Выберем параметры, аналогичные параметрам в [5]. [13, 26]:параметры полости c как [13]: g ₀ =12 ГГц / нм, γ _м =41 кГц, ω _м =51,8 МГц, κ _c =5 МГц, м =20 нг, λ =750 нм, и Q =1500, а мощность накачки по порядку величины составляет милливатт (1 мВт =10 ⁻³ W). Для полости a , считаем ω _а = ω _c и κ _c = κ _а . Сила сцепления Дж между двумя режимами резонатора играет ключевую роль и может повлиять на бистабильное поведение и FWM. Экспериментально сообщалось, что прочность связи J зависит от расстояния между полостями c и полость a [26] (также сила связи экспоненциально уменьшается с увеличением расстояния между двумя полостями). Здесь мы ожидаем силу сцепления \ (J \ sim \ sqrt {\ kappa _ {c} \ kappa _ {a}} \).

Уравнения (10) и (11), определяющие внутрирезонаторное число фотонов оптомеханического резонатора c и обычная полость a являются связанными кубическими уравнениями, которые демонстрируют бистабильное поведение. Сначала рассмотрим условие J =0, т.е. только один оптомеханический резонатор c , а на рис. 2а показано среднее число внутрирезонаторных фотонов n _c оптомеханической полости c как функция отстройки винтового насоса Δ _c = ω _c - ω _p с тремя мощностями накачки. Когда мощность насоса меньше P =0,4 мВт (например, P =0,1 мВт) кривая близка к лоренцевой. При увеличении мощности P до критического значения, оптомеханическая полость c демонстрирует бистабильное поведение, как показано на кривых для P =От 0,4 мВт до P =0,8 мВт, где кривая первоначально лоренцевского резонанса становится асимметричной. Среднее число фотонов внутри резонатора n _c имеет три действительных корня (уравнение (10)), причем наибольший и наименьший корни являются устойчивыми, а средний - неустойчивым, что показано овалом на рис. 2а. Однако, когда мы рассматриваем оптический резонатор a , т.е. J ≠ 0, например J =1,0 κ _а , бистабильное поведение некоторым образом нарушается, как показано на рис. 2b. Это потому, что, когда оптомеханическая полость c соединен с оптическим резонатором a , части числа внутрирезонаторных фотонов n _c оптомеханической полости c будет соединен с оптическим резонатором a , и, следовательно, число фотонов внутри резонатора n _c уменьшится, а затем приведет к разрушению бистабильного поведения. На рисунке 2c показано среднее число фотонов внутри резонатора n . _c оптомеханической полости c как функция силы связи между полостью J с тремя мощностями накачки. Очевидно, среднее число фотонов внутри резонатора n _c зависит от мощности насоса P , а число внутрирезонаторных фотонов n _c всегда уменьшается с увеличением силы связи J потому что части числа фотонов попадают в оптический резонатор a . Кроме того, большая расстройка резонатора-накачки полезна для наблюдения оптического бистабильного поведения при увеличении мощности накачки P . На рисунке 2d показано среднее число фотонов внутри резонатора n . _c от мощности насоса P с полостью a на красных боковых полосах ( Δ _а = ω _м ) и синие боковые полосы ( Δ _а =- ω _м ) соответственно, а бистабильность представляет собой поведение петли гистерезиса [50]. Однако наши результаты отличаются от предыдущей работы по двухмодовой оптомеханической системе без учета связи резонатор-резонатор J . Следовательно, прочность связи J играет важную роль в бистабильности.

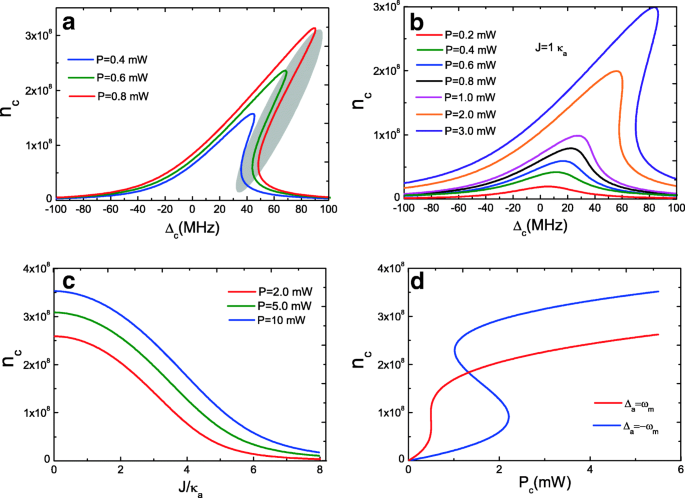
а Среднее число внутрирезонаторных фотонов оптомеханического резонатора c как функция отстройки винтового насоса Δ _c с тремя мощностями накачки при Дж =0. б Среднее число внутрирезонаторных фотонов оптомеханического резонатора c как функция отстройки винтового насоса Δ _c с несколькими разными мощностями накачки под Дж =1,0 κ _а . c Среднее число внутрирезонаторных фотонов n _c оптомеханической полости c как функция от J с тремя мощностями накачки. г Среднее число внутрирезонаторных фотонов n _c как функция от P для Δ _c = Δ _а = ω _м

Мы дополнительно исследуем бистабильное поведение оптического резонатора a с формулой. (11). На рис. 3а показано число фотонов в резонаторе n . _а обычной полости a как функция отстройки винтового насоса Δ _а = ω _а - ω _p с мощностью насоса P =0,1 мВт, P =1,0 мВт, и P =10 мВт при Дж =1,0 κ _а . Очевидно, что оптический резонатор a не может вести себя как бистабильное поведение из-за количества фотонов внутри резонатора n _а полости a из полости c не может поддерживать бистабильность при малой мощности накачки. Собственно только накачка большой мощности P может впадать a присутствует бистабильное поведение, потому что только оптомеханический резонатор с мощной накачкой c , гораздо большее количество фотонов может попасть в оптический резонатор a . Мы также наносим на график среднее число фотонов внутри резонатора n _а оптического резонатора a как функция силы связи J при трех мощностях накачки, как показано на рис. 3b. Понятно, что когда J =0, n _а =0, потому что нет связи между двумя полостями при J =0, и при этом условии ни один фотон не попадает в оптический резонатор a . При увеличении прочности сцепления Дж (уменьшая расстояние между двумя полостями [26]), количество внутрирезонаторных фотонов n _а обычного оптического резонатора a увеличиваются, но не всегда. Имеется оптимальная сила сцепления Дж для максимального значения n _а при разной мощности накачки, а затем, n _а будет уменьшаться с увеличением J . Примечательно, что прочность связи J между двумя полостями можно регулировать [26].

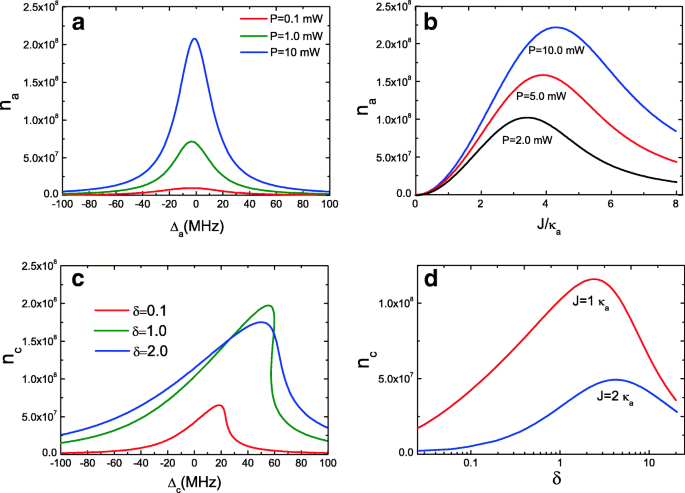
а Среднее количество фотонов в обычном резонаторе a как функция отстройки винтового насоса Δ _а с тремя мощностями накачки при Дж =1,0 κ _а . б Среднее число внутрирезонаторных фотонов n _а как функция от J с тремя мощностями накачки. c Среднее число внутрирезонаторных фотонов n _c как функция от Δ _c с тремя параметрами отношения δ . г Среднее число внутрирезонаторных фотонов n _c как функция от δ на двоих J

Кроме того, мы рассматриваем коэффициент отношения δ = κ _c / κ _а ( κ _c = ω _c / Q _c и κ _а = ω _а / Q _а ) для исследования параметров двух резонаторов, которые влияют на бистабильное поведение. κ - скорость затухания моды резонатора, которая связана с частотой и добротностью резонатора. Как мы знаем, одновременно добиться высоких значений Q и малых V для режима резонатора затруднительно из-за дифракционного предела. Для оптического резонатора меньшее значение V, соответствующее большей скорости радиационного распада, приводит к более низкому значению Q. Хотя разные типы резонаторов обладают своими уникальными свойствами, разница между высоким Q и малым V все же существует. Однако, если связать исходную OMS c с высокой диссипацией резонатора в режим вспомогательного резонатора a при высоком Q, но большом V бистабильное поведение существенно изменится. На рисунке 3c показано среднее число фотонов внутри резонатора n . _c оптомеханической полости c как функция от Δ _а при нескольких разных δ = κ _c / κ _а с неизменной силой сцепления Дж =1,0 κ _а . Мы можем обнаружить, что бистабильное поведение может появиться, но число фотонов внутри резонатора n _c мала при δ =0,1 с J =2 κ _а , т.е. κ _c =0,1 κ _а что означает Q _c > Q _а . При увеличении коэффициента δ от δ =От 1,0 до δ =2,0, число фотонов внутри резонатора n _c испытывает изменение от бистабильного поведения к профилю почти лоренцевой линии. То есть, когда Q _c < В _а , бистабильное поведение будет нарушено, но существует оптимальное условие, т. е. Q _c = Q _а . На рис. 3d мы даем число фотонов внутри резонатора n _c как функция от δ с двумя разными J , и, очевидно, при увеличении параметра отношения δ , количество внутрирезонаторных фотонов n _c увеличивать. Когда он достигает оптимального значения для данного J , затем n _c снижаться. Следовательно, контролируя параметры резонатора, такие как скорость распада κ или добротность резонаторов, бистабильное поведение можно контролировать.

С другой стороны, как типичное нелинейно-оптическое явление, мы также исследуем процесс ЧВВ с помощью уравнения (1). (14) в оптико-механической системе фотонных молекул. На рисунке 4 показан спектр FWM в зависимости от резонатора зонда a отстройка Δ _s = ω _s - ω _а в Δ _а = Δ _c =0 при различных режимах параметров. На рис. 4a – d представлена ​​эволюция спектров ЧВВ при различной мощности накачки P . в J =1,0 κ _а . Ясно, что в спектрах ЧВВ присутствуют три пика, из которых лоренцев пик около Δ _s =0, и два пика расщепления мод расположены на ± ω _м , а интенсивность ЧВВ уменьшается с увеличением мощности накачки. На рис. 4e – h показано изменение спектров FWM от J =0,5 κ _а кому: J =2,0 κ _а при мощности накачки P =1,0 мВт. При увеличении прочности сцепления Дж от J =0,5 κ _а кому: J =2,0 κ _а , спектры ЧВВ существенно изменяются. Явление можно объяснить с помощью картины одетого состояния, которая была продемонстрирована в оптико-механической системе с одним резонатором [51].

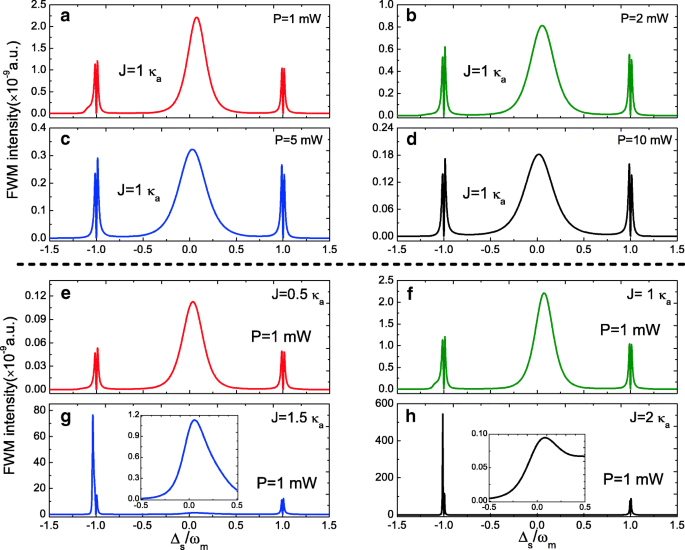
а - г Интенсивность ЧВВ как функция нормированной отстройки зонд-накачка Δ _s для разной мощности накачки при Дж =1,0 κ _а . е - ч Интенсивность FWM как функция от Δ _s для разных J при мощности накачки P =1,0 мВт

Затем мы исследуем спектры ЧВВ при Δ _а = Δ _c ≠ 0. На рис. 5a – d показаны спектры FWM в красной боковой полосе, т. Е. Δ _а = Δ _c = ω _м под неизменным J =1,0 κ _а при увеличении мощности накачки от P =От 1,0 до P =10 мВт. В спектрах FWM появляются два пика нормального расщепления мод при ± ω _м соответственно, а интенсивность ЧВВ уменьшается с увеличением мощности накачки. На рис. 5e – h показаны спектры FWM в красной боковой полосе, т. Е. Δ _а = Δ _c = ω _м при фиксированной мощности насоса P =2,0 мВт при увеличении силы связи Дж от J =0,5 κ _а кому: J =2,0 κ _а . Очевидно, что интенсивность FWM увеличивается с увеличением силы связи J , а больший J означает большее количество фотонов, подключенных к оптическому резонатору a . При изменении отстройки Δ _а и Δ _c от красной боковой полосы к синей боковой полосе, т. е. Δ _а = Δ _c =- ω _м , существенно меняется эволюция спектров ЧВВ. На рис. 5i – l показаны спектры FWM в синей боковой полосе при четырех различных мощностях накачки, а интенсивность FWM уменьшается с увеличением мощности накачки даже в синей боковой полосе. За исключением двух пиков нормального расщепления мод, расположенных на ± ω _м , в спектрах FWM также появляются два острых пика боковых полос, положение которых связано с мощностью накачки. На рис. 5m – p мы также обсуждаем силу связи J которые влияют на спектры FWM под синей боковой полосой. Появление других острых пиков боковых полос в спектрах FWM зависит от силы связи J .

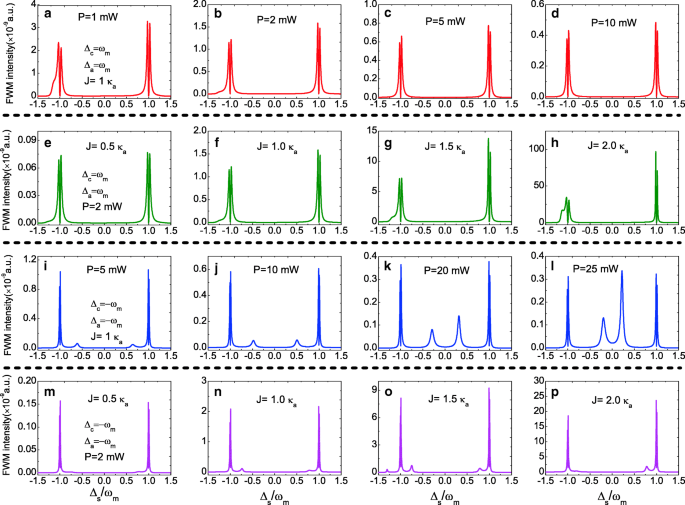
а - г Интенсивность FWM как функция от Δ _s для разной мощности насоса P на красной боковой полосе ( Δ _c = Δ _а = ω _м ) и J =1,0 κ _а . е - ч Интенсивность FWM как функция от Δ _s для разных J под красной боковой полосой и мощность накачки P =2,0 мВт. я - l Интенсивность FWM как функция от Δ _s для разной мощности насоса P на синей боковой полосе ( Δ _c = Δ _а =- ω _м ) и J =1,0 κ _а . м - п Интенсивность FWM как функция от Δ _s для разных J под синей боковой полосой и мощность накачки P =2,0 мВт

Далее, поскольку параметр отношения δ = κ _c / κ _а может влиять на количество внутрирезонаторных фотонов в составной фотонной молекуле OMS, спектры FWM можно изменять, управляя параметром δ . На рис. 6а – з представлены спектры ЧВВ при неизменных параметрах J =2,0 κ _а и P =10 мВт под красной боковой полосой при увеличении отношения δ от δ =От 0,05 до δ =3.0, а интенсивность ЧВВ уменьшается с увеличением отношения δ . Находясь в синей боковой полосе, в спектрах FWM появятся другие острые пики боковых полос, как показано на рис. 6i – p, а интенсивность FWM также уменьшается с увеличением отношения δ . Следовательно, контролируя параметры резонатора, такие как скорость распада κ или добротности полостей, FWM может легко достичь в композитном фотонно-молекулярном OMS.

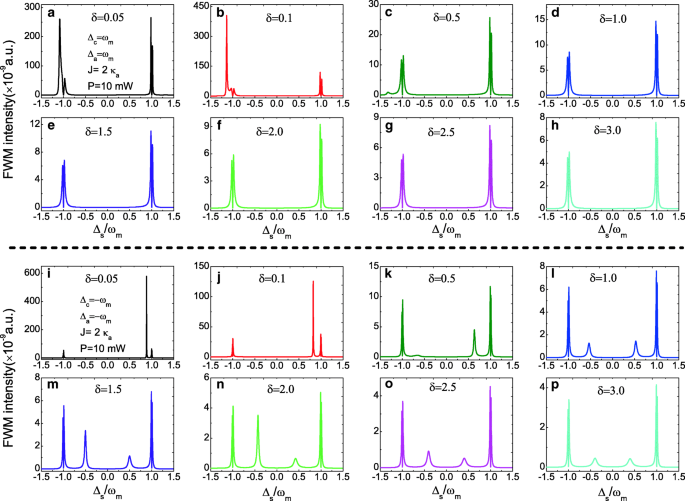
а - ч FWM intensity as a function of Δ _s for several different ratio parameters δ at the red sideband (Δ _c =Δ _а =ω _м ) and J =2.0 κ _а , P =10 mW. я –p FWM intensity as a function of Δ _s for several different ratio parameters δ at the blue sideband (Δ _c =Δ _а =−ω _м ) and J =2.0 κ _а , P =10 mW

Заключение

We have investigated the optical bistability and four-wave mixing in a composite WGM cavity photonic-molecule optomechanical system, which includes an optomechanical cavity with high-cavity dissipation coupled to an auxiliary cavity with high-quality factor. We investigate the optical bistability under different parameter regimes such as the coupling strength J between the two cavities and the decay rate ratio δ of the two cavities in the system. The optical bistability can be adjusted by the pump field driving the optomechanical cavity, and the intracavity photon number in the two cavities is determined by the coupling strength J . Further, we have also demonstrated how to control the FWM process in the photonic-molecule optomechanical system under different driving conditions (the red sideband and the blue sideband) and different parameter conditions (the coupling strength J и отношение δ ). Numerical results show that the FWM process can be controlled with such parameters. These results are beneficial for better understanding the nonlinear phenomena in the composite photonic-molecule optomechanical system.

Сокращения

C-OMS:

Cavity optomechanics systems

FWM:

Four-wave mixing

OMS:

Optomechanics systems

OMIT:

Optomechanically induced transparency

Q:

Quality

V:

Volume

WGM:

Whispering gallery mode