Частотно-модулированный волновой диэлектрофорез везикул и клеток:периодические развороты на частоте кроссовера

Фон

Поляризуемость электрического фенотипа в первую очередь обусловлена ​​клеточной мембраной и электрическими свойствами цитоплазмы, которые зависят от частоты приложенного электрического поля. Соответственно, отдельные клетки могут быть идентифицированы по различиям в диэлектрических спектрах с использованием неинвазивных электрических методов. В настоящее время электрические методы пригодны для отделения клеток с полезными фенотипами от неизвестных образцов [1–15]. По сравнению с другими методами разделения, они предлагают главное преимущество, заключающееся в том, что не требуется модификация клеток с помощью антител или присоединение к чужеродному материалу, что позволяет избежать возможности повреждения или активации клеток этими зондами [1–16]. Характеристика диэлектрических свойств ячеек была выполнена в основном с использованием либо спектроскопии импеданса [10, 12, 13], либо электрокинетики переменного тока (AC), такой как диэлектрофорез (DEP), DEP бегущей волны (twDEP) и электровращение [1, 9, 15]. Среди них мы сосредоточены на расширении метода AC-DEP для разработки нового метода определения диэлектрических характеристик с использованием частотно-модулированных (FM) волн вместо полей переменного тока.

В общем, DEP возникает в градиенте электрического поля, который создает электрокинетическую силу, действующую на любой поляризуемый объект, заряженный или нейтральный, в направлении, определяемом не только вектором градиента, но и действительной частью уравнения Клаузиуса-Моссотти ( CM) фактор [1–15, 17–21]. Например, мы рассматриваем силу DEP, индуцированную электрическим полем переменного тока E _AC ( г , t ), пространственно-временная зависимость которого выражается как E _AC ( г , t ) = А ( г ) cos θ _AC ( г , t ) с использованием вектора амплитуд A ( г ) и фаза θ _AC ( г , t ). Сила AC-DEP создается пространственным градиентом амплитуды (т. Е. ∇ A ), умноженное на действительную часть фактора CM, как упомянуто выше, тогда как пространственный градиент фазы (т.е. ∇ θ _AC ), умноженное на мнимую часть коэффициента CM, создает силу либо twDEP, либо электровращение, что, таким образом, обеспечивает дополнительную информацию для метода AC-DEP с точки зрения диэлектрических характеристик [9, 15, 20, 21].

В этом письме мы стремимся сформулировать силу DEP, индуцированную FM-полем, и сравнить методы AC- и FM-DEP, так что ни AC, ни FM-поле не учитывают пространственную зависимость фазы; поэтому мы установим θ _AC ( т ) =2 π е _AC т пропорционально приложенной частоте f _AC . Важной особенностью AC-DEP является то, что направление силы, а также ее сила зависят от f _AC . В частности, направление силы меняется на противоположное на частоте кроссовера f . _AC = f _X из-за изменения знака действительной части фактора CM, который оказался доступным для определения диэлектрических характеристик с помощью AC-DEP [1–15].

Частотная зависимость силы AC-DEP также сделала возможными следующие манипуляции [1–15, 22–31]:электрически управляемый захват, фокусировка и перемещение коллоидных частиц, а также фракционирование и характеризация живых и / или мертвые клетки. В традиционных системах для диэлектрофоретической сборки и / или манипулирования коллоидными частицами часто используются микроизготовленные электроды, между которыми электрическое поле переменного тока прикладывается к коллоидным суспензиям, благодаря недавним быстрым достижениям в производстве интегрированных полупроводниковых устройств [24–30]. . Эта технология, предлагающая бесконтактное манипулирование, в настоящее время интегрируется с различными системами «лаборатория на кристалле», которые обеспечивают преимущество точного и повторяемого манипулирования. Тем не менее, электроды на кристалле, которые создают пятна высокой интенсивности в полях переменного тока, не могут изменять свое положение независимо от держателя образца, в отличие от лазерного фокуса, который можно свободно позиционировать при оптических манипуляциях. Из ограничений систем на кристалле следует, что предыдущие методы DEP представляли некоторую трудность и сложность при выполнении типов операций, для которых подходят оптические пинцеты. Одним из возможных методов преодоления этих трудностей является DEP с оптическим изображением [32].

Здесь мы использовали, как более простую альтернативу, один из методов электронного пинцета [22, 23, 33–38] для диэлектрофоретической сборки и / или манипуляции по требованию без оптического устройства (см. Рис. 1). Как видно из рис. 1, в нашей системе с подключаемым модулем используется пара игл микроэлектродов, которые управляются микроманипуляторами для приложения внешних электрических полей в коллоидной суспензии. Электродные зонды не были фиксированными, а были подвижными в коллоидных суспензиях из-за их вставного типа. Однако остается существенное требование для практического использования диэлектрических характеристик:продолжительность приложения электрического поля к элементам, окруженным солеными электролитами, должна быть минимизирована. Например, метод AC-DEP включает использование встречно-гребенчатых электродов, которые встроены в микрофлюидную систему, так что переменные поля различной частоты могут одновременно применяться в суспензии клеток [24–30]. В то время как такие усовершенствованные системы на кристалле были признаны подходящими для определения диэлектрических характеристик, метод многоэлектродных пар неприменим к одноэлектродно-парной системе, которая часто используется в методах электронного пинцета [22, 23, 33–38]. .

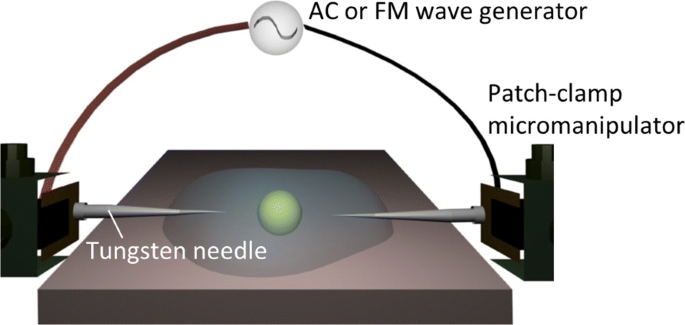
Экспериментальная установка. Схема системы диэлектрофоретической манипуляции, иллюстрирующая электрическое поле переменного или FM, приложенное к целевой частице через пару игл электродов, управляемых микроманипуляторами с фиксатором.

Для проведения одновременных многочастотных измерений с использованием одноэлектродно-парной системы (рис. 1) необходимо исследовать изменение приложенного электрического поля. В этом письме мы обращаемся к доступности изменяющегося во времени DEP из-за FM-волны (FM-DEP) следующей формы:

где фаза θ ( т ) FM-волны связана с мгновенной частотой f ( т ) как 2 π е ( т ) = d θ ( т ) / d т и

с f _м обозначающая частоту модуляции. Мы используем широкополосный FM, удовлетворяющий тому, что Δ е / f _м ≫1, так что условия f _м / f ( т ), f _м / f _c , f _м / Δ е ≪1 будет называться пределом широкой полосы (WBL) в теоретической формулировке, приведенной ниже.

В этом письме особое внимание уделяется соотношению между характеристической частотой f _X и траектория FM-DEP. В следующем разделе мы описываем как используемые материалы, так и детали системы плагинов для создания FM-DEP. В третьем разделе представлены результаты и обсуждение, состоящее из четырех частей. Во-первых, мы исследуем детали повторяющихся разворотов одной лейкозной клетки путем количественной оценки возвратно-поступательной траектории, периодичность которой объясняется частотой модуляции f _м , или периодические колебания f ( т ), задаваемый формулой. (2). Затем мы теоретически объясним возвратно-поступательную траекторию, выведя изменяющуюся во времени диэлектрофоретическую силу, которая модулируется в соответствии с мгновенной частотой f ( т ) FM-поля, удовлетворяющего условию WBL. Полученный вид диэлектрофоретической силы дает уравнение, определяющее f _X от наблюдаемых разворотов. В-третьих, мы измеряем величину диэлектрофоретической силы на многослойной везикуле (MLV), которая была прикреплена к игле электрода из-за притяжения AC-DEP. Частотная зависимость силы была аппроксимирована с использованием спектрального уравнения, которое было определено из действительной части фактора CM, так что f _X определялась как характерная частота, при которой сила притяжения из-за AC-DEP обращается в нуль. Поскольку метод FM-DEP также дает f _X анализируя возвратно-поступательную траекторию MLV, мы оцениваем степень совпадения между частотами кроссовера, оцененными с помощью AC- и FM-DEP. Наконец, как проводимость цитоплазмы, так и емкость мембран трех типов клеток были оценены с помощью f _X как возрастающая функция проводимости раствора, и полученные значения сравнивались с данными, приведенными в литературе.

Методы

Материалы

Для приготовления многослойных везикул (MLV) мы использовали 1,2-диолеоил-sn-глицеро-3-фосфатидилхолин (DOPC) в качестве липидов, приобретенных в Avanti Polar Lipids. MLV были получены с помощью следующей процедуры. ДОФХ (1 мл, 20 мМ), растворенный в хлороформе / метаноле (2:1 об / v ) сушили N ₂ газа, а растворитель полностью удаляли в вакууме более 12 ч. Тонкую пленку, осаждавшуюся на стеклянном флаконе в результате испарения, регидратировали с использованием деионизированной воды и инкубировали при 25 ° C в течение нескольких часов.

В экспериментах использовали две клеточные линии:JKT-beta-del линии Т-клеточного лейкоза человека (TL) и CCRF-SB линии В-клеточного лейкоза человека (BL). Оба типа клеток TL и BL использовали после 1 недели инкубации в увлажненном инкубаторе, содержащем 5 % CO ₂ на 37, так что у нас были концентрации клеток в пределах 0,5 × 10 ⁶ до 1 × 10 ⁶ клеток / мл. В среду RPMI 1640 для клеточной культуры добавляли 10% фетальную сыворотку бровиновой кислоты и 100 мМ пирувата натрия. Клетки осаждали центрифугированием при 370 g . в течение 3 мин дважды, чтобы клетки можно было полностью ресуспендировать в 1 мл среды RPMI 1640 перед пипетированием. Полученные клеточные суспензии дополнительно разбавляли изотоническим 200 мМ раствором сахарозы, чтобы приготовить растворитель, имеющий требуемую проводимость.

Мы также использовали клетки красной крови (RB) человека, диспергированные в следующих суспензиях. Свежеотобранные образцы цельной крови были получены от здоровых добровольцев в возрасте от двадцати пяти лет. Клетки, суспендированные в смеси среды RPMI 1640 и гематокрита 3,1%, разбавляли изотоническим 200 мМ раствором сахарозы для приготовления растворителя, имеющего требуемую проводимость, а также указанных выше лейкозных клеток. Все диэлектрофоретические эксперименты с использованием человеческих RB-клеток были завершены в течение 10 минут после отбора образцов цельной крови.

Экспериментальная установка

Электропроводность клеточных суспензий измеряли с помощью кондуктометра (SevenMulti, Mettler-Toledo, Columbus, OH, USA). Схема используемой сменной системы показана на рис. 1. Внешнее электрическое поле с волной переменного или FM-диапазона прикладывалось через генератор сигналов произвольной формы (Agilent 33220A, Agilent Technologies, Санта-Клара, Калифорния, США) с током усилитель (F30PV, FLC Electronics, Partille, Швеция), к которому подключались вставные микроэлектроды. Микроэлектроды представляли собой вольфрамовые иглы с диаметром острия 0,5 мкм . m, которые независимо контролировались двумя наборами микроманипуляторов patch-clip (NMN-21, Narishige, Setagaya-ku, Tokyo, Japan). Во всех последующих экспериментах мы поддерживали расстояние между наконечниками на уровне 100 μ . м при приложении внешних полей к вышеуказанным подвескам, а максимальная величина была установлена ​​равной 0,5 кВ / см. Пару игл вставляли в каплю образца, установленную на инвертированном оптическом микроскопе (TE2000-U, Nikon, Minato-ku, Токио, Япония), и оптические микрофотографии получали с помощью камеры CCD (Retiga Exi, QImaging, Surrey, British Колумбия, Канада) с частотой кадров 25 кадров в секунду; кстати, было подтверждено, что разрешение по частоте FM-волн из-за частоты кадров всегда находилось в пределах шкалы ошибок для каждого вида данных. 50- мкм 1 каплю суспензии помещали на предметный столик инвертированного оптического микроскопа, температура которого поддерживалась на уровне 25 ° C с помощью терморегулятора.

Техника подключаемого модуля позволяет простой системе выполнять различные бесконтактные манипуляции с отдельной ячейкой, такие как проталкивание ее в узкий канал без какого-либо контакта и ориентация в желаемом направлении. Хотя часто необходимо обрабатывать клетки в изотоническом растворе с солью, проще всего реализовать описанные выше манипуляции с DEP с клетками, окруженными деионизированной водой. В дополнительном файле 1:фильмы с S1 по S3 система плагинов индуцировала AC-DEP клеток диатомовых водорослей, взвешенных в деионизированной воде. Из Дополнительного файла 1:Фильмы с S1 по S3 видно, что анизотропная клетка диатомовой водоросли, диспергированная в бессолевой воде, обрабатывалась парой микроэлектродов, между которыми было приложено электрическое поле переменного тока (1 кВ / см), как наклейка с наклейкой. . Бесконтактные операции состоят из трех этапов:(i) целевая ячейка сначала вращалась параллельно стеклянной стенке, положительно заряженной за счет комбинации настройки диполя с частотой 30 кГц и изменения положения каждого микроэлектрода (дополнительный файл 1:Movie S1 ), (ii) мы впоследствии изменили частоту на 100 кГц, чтобы подтолкнуть ее к стене, чтобы электростатически зафиксировать ячейку запроса с отрицательными зарядами на поверхности стекла (дополнительный файл 1:Movie S2), и (iii) частота переменного тока была скорректирована до 20 МГц для наведения AC-DEP в противоположном направлении, чтобы электростатически прикрепленный элемент можно было вытащить (дополнительный файл 1:Movie S3).

Результаты и обсуждение

Экспериментальное наблюдение лейкозной клетки, испытывающей FM-DEP

Наши сменные микроэлектроды (см. Рис. 1) позволяют приложить электрическое поле к частицам, плавающим далеко над подложкой образца, что имеет практическое применение для выбора подходящих ячеек. Например, Дополнительный файл 1:Фильм S4 показывает, что пара микроэлектродов контролировалась для приближения к плавающей треугольной диатомовой ячейке, к которой мы приложили электрическое поле переменного тока с его частотой, скачкообразной между 100 и 500 кГц с интервалами 0,5 с. В дополнительном файле 1:Movie S4 мы видим, как треугольная ячейка подпрыгивает на микроэлектроде из-за скачка частоты в качестве предварительного результата перед следующей манипуляцией с использованием FM-DEP.

Дополнительный файл 1:фильмы S5 и S6 демонстрируют типичное поведение нескольких TL-клеток, испытывающих FM-DEP, которые аналогичны поведению клеток млекопитающих, манипулируемых электронным пинцетом с использованием единственного электрода AC-DEP [36]. На рисунке 2 изображена одна из периодических траекторий с использованием трехмерного графика ( x , y ) вдоль t ось, где относительная координата ( x , y ) назначается временному положению ячейки с исходной точкой (0, 0), расположенной в определенной точке иглы микроэлектрода для извлечения конфигурации ячейка-электрод. Хотя x ось представляет собой касательную к поверхности электрода в точке (0, 0), y ось, перпендикулярная касательной, в основном отражает проекцию периодических разворотов, описанных ниже. На рис. 2 мы выбрали плавающую ячейку ЛЭП, к которой мы приложили электрическое поле ЧМ с частотой модуляции f . _м установлен на f _м =0,25 Гц в диапазоне 200 кГц ≤ f ( т ) ≤ 3 МГц. Потому что у нас есть Δ е / f _м , f ( т ) / f _м <10 ⁻⁵ , условие WBL действительно выполняется, как упоминалось после уравнения. (2).

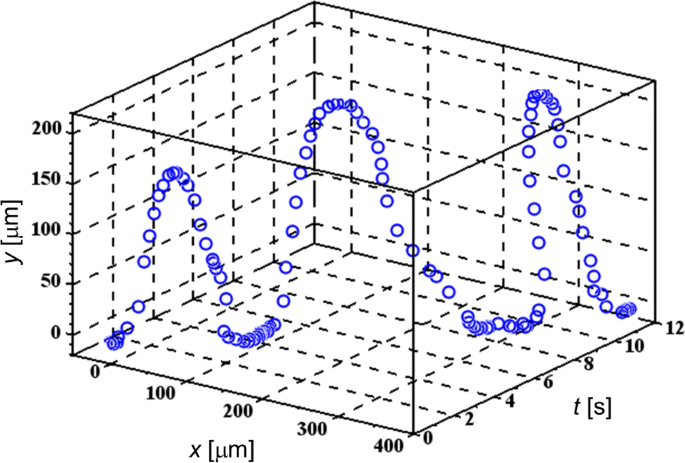
Трехмерная траектория целевой ячейки TL. Периодические развороты из-за частотной модуляции демонстрируются для соты TL, подвергающейся FM-DEP

Из Дополнительного файла 1:Фильмы S5 и S6, а также из Фиг.2 видно, что периодическая траектория состоит из трех частей ухода, приближения и пребывания на микроэлектроде:(i) ячейка покидает микроэлектрод, (ii) он приближается к микроэлектроду после поворота на 180 градусов и (iii) остается на поверхности микроэлектрода. Ячейка часто не может вернуться в то же положение на поверхности микроэлектрода из-за потока растворителя, который не только наблюдается в Дополнительном файле 1:Фильм S6, но также представлен разворотами, когда ячейка мигрирует в <я> х Направление на рис. 2. Несмотря на интерференцию с потоком растворителя, можно выделить моменты, когда ячейка начинает отрываться от поверхности микроэлектрода и делает разворот по периодической траектории соответственно. Соответственно, из рис. 2 видно, что эти развороты повторяются с интервалами 4 с в совпадении с частотой модуляции 0,25 Гц или 4-секундным периодом мгновенной частоты f ( т ).

Теоретическое исследование FM-DEP

Чтобы объяснить экспериментальные траектории, в том числе периодические U-образные повороты, мы рассматриваем сферический объект как упрощенную модель одиночной ячейки, к которой действует произвольное изменяющееся во времени электрическое поле E ( г , t ) применены. На рисунке 3 схематически показана зависящая от времени сила DEP, действующая на сферический объект [9]. Как показано на рис. 3, диэлектрическая проницаемость и проводимость внутри сферического объекта представлены как ε _в и σ _в соответственно, и нижний индекс «out», например ε _вне и σ _вне , обозначает внешнюю сторону. В общем, F _DEP ( г , t ) связана с наведенным дипольным моментом p ( г , t ) как [17–19]

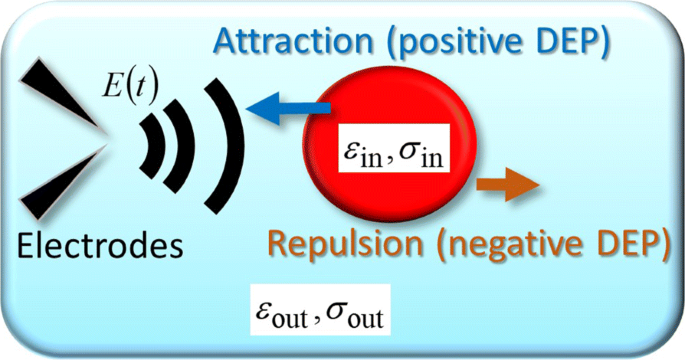
Теоретическая модель. Схематическое изображение силы FM-DEP, действующей на ячейку, которая моделируется как модель однородной сферы с диэлектрической проницаемостью и проводимостью ε _в и σ _в , соответственно. Сфера окружена электролитной средой с диэлектрической проницаемостью и проводимостью ε . _вне и σ _вне , соответственно. Модель однородной сферы - это упрощение модели сферической единственной оболочки, которая рассматривает клетку как размазанную цитоплазму, окруженную мембраной [9]

где K _H и Δ τ определяются следующим образом: K _H =( ε _в - ε _вне ) / ( ε _в +2 ε _вне ) и \ (\ Delta \ tau ^ {- 1} =\ tau _ {0} ^ {- 1} - \ tau ^ {- 1} \) с использованием радиуса R сферического объекта и два характерных времени τ ₀ =( ε _в - ε _вне ) / ( σ _в - σ _вне ) и τ =( ε _в +2 ε _вне ) / ( σ _в +2 σ _вне ).

Подстановка переменного электрического поля E _AC ( г , t ) = А ( г ) cos (2 π е _AC т ) в уравнения. (3) - (5), получаем среднюю силу DEP < F _DEP ( г , t )>, усредненное по циклам переменного поля [9, 15, 20]:

где A _RMS обозначает среднеквадратичный вектор (RMS), удовлетворяющий тому, что \ (\ boldsymbol {A} _ {\ text {RMS}} ^ {2} =\ boldsymbol {A} ^ {2} / 2 \) и χ ( е _AC ) ≡2 π R ³ ε _вне Re [ K ( е _AC )] зависит от применяемой частоты f _AC из-за Re [ K ( е _AC )], действительная часть фактора CM [9, 15, 20]:

где K _L =( σ _в - σ _вне ) / ( σ _в +2 σ _вне ) и K _H , определенные выше, соответствуют реальным значениям CM в пределах низких и высоких частот, соответственно, и этим предельным значениям, K _L и K _H , должны иметь противоположные знаки, чтобы f _X определяется как χ ( е _X ) =0 может существовать [9, 15, 20].

Уравнения (6) и (7) показывают, что электрическое поле переменного тока создает силу DEP, направление которой зависит от приложенной частоты f _AC через χ ( е _AC ), задаваемый формулой. (7), который объясняет подпрыгивающую клетку диатомовой водоросли в дополнительном файле 1:Movie S4 следующим образом (см. Также рис. 3). Когда приложенная частота обеспечивает знак плюс действительной части коэффициента CM (т. Е. χ ( е _AC )> 0), мы можем наблюдать клетки, притянутые к концам игл электрода (положительный DEP), на которые сила переменного поля, приложенного через пару игл электрода, является наибольшей. Знак реального коэффициента CM может быть изменен на отрицательный при f _X , исчезающая частота реального фактора CM (т. е. χ ( е _X ) =0), где у нас есть нулевая диэлектрофоретическая сила, найденная из уравнения. (6). В отрицательном знаке фактора CM (т. Е. χ ( е _AC ) <0) отдельные коллоиды отталкиваются от пары электродов-игл (отрицательный DEP). Треугольная диатомовая ячейка в дополнительном файле 1:Movie S2 отскакивает из-за противоположного направления AC-DEP, индуцированных полями переменного тока с их частотами 100 и 500 кГц; комбинируя уравнение. (6) и наблюдаемые диэлектрофоретические направления, находим, что χ (100 кГц)> 0 и χ (500 кГц) <0.

Затем мы рассмотрим FM-DEP, подключив фазу, заданную уравнениями. (1) и (2) в уравнения. (3) - (5). Как показано в Дополнительном файле 2, условие WBL FM-волны подтверждает приближенную форму интегрирования в уравнении. (5), тем самым обеспечивая

который принимает ту же форму, что и AC-DEP, когда зависящая от времени частота f ( т ) заменяется постоянной частотой f _AC . Таким образом, мы получаем предельный вид средней силы ДЭП < F _DEP ( г , t )>, усредненное по циклам θ ( т ) в поле FM (см. уравнения (A1), (A13) и (A14) в дополнительном файле 2):

имеет форму, аналогичную формуле. (6) для AC-DEP. Разница в том, является ли коэффициент при χ { е ( т )} зависит от t через f ( т ), который циклически изменяется в соответствии с частотной модуляцией с периодом T _м =1 / f _м .

Основываясь на простом выражении (9) FM-DEP, мы проиллюстрируем с помощью рис. 4 механизм указанных выше разворотов из-за FM-волны. На рисунке 4 показана схема DEP, вызванного FM-волной в WBL, когда диапазон f ( т ) покрывает частоту кроссовера f _X такие, что f _c - Δ е ≤ f _X ≤ f _c + Δ е . На рис. 4 предполагается, что частотная зависимость действительной части фактора CM, или χ { е ( т )}, обеспечивает замену знака следующим образом:знак минус ( χ { е ( т )} <0) для f ( т ) < f _X и знак плюса ( χ { е ( т )}> 0) для f ( т )> f _X , что и имеет место в наших экспериментах. Первый период, удовлетворяющий f ( т ) < f _X имеет время продолжительности, тогда как последнее f ( т )> f _X был сохранен в течение остального периода:один цикл подразделяется на два периода, которые отмечены красным и синим цветом, соответственно, на рис. 4.

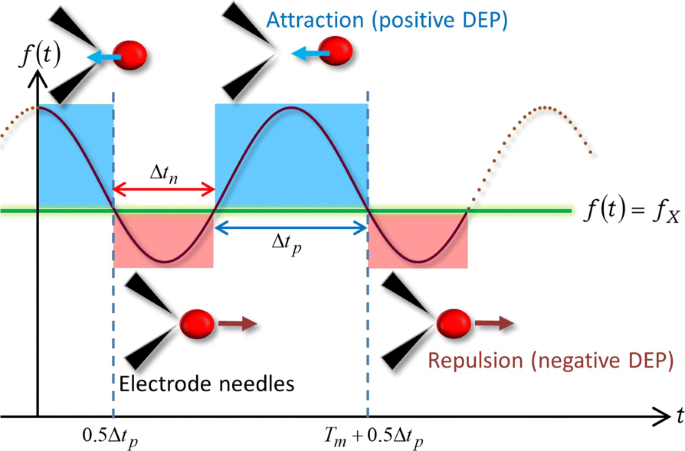
Направление силы связано с частотной модуляцией. Иллюстрация периодических разворотов из-за FM-волны с зависящей от времени частотой f ( т ), покрывающего частоту кроссовера f _X

Аналогично AC-DEP, уравнение. (9) означает, что знак минус ( χ { е ( т )} <0) создает силу отталкивания DEP между ячейкой и микроэлектродами, удовлетворяя при этом f ( т ) < f _X . В результате ячейка покидает область вокруг кончиков игл микроэлектрода, между которыми величина электрического поля наибольшая:ячейка испытывает отрицательную DEP в течение красного периода Δ т _n на рис. 4. В момент t _X как решение f ( т _X ) = f _X , χ ( е ) исчезает с последующим изменением знака на χ ( е )> 0, а f ( т )> f _X , и, соответственно, сила DEP переключается на силу притяжения в t _X . После разворота на t _X из-за изменения направления силы DEP, целевая ячейка начинает приближаться к микроэлектроду, перемещающемуся в противоположном направлении, и в конечном итоге оказывается зажатой между кончиками электродных игл или прикрепляется к одному из электродов:ячейка испытывает положительную DEP во время синий период Δ т _p на рис. 4. На рис. 4 показано, что цикл выхода, приближения и пребывания на микроэлектроде должен повторяться с периодом модуляции T _м , в соответствии с рис. 2: Δ т _n + Δ т _p = Т _м . Таким образом, диэлектрофоретический механизм, изображенный на рис. 4, может объяснить периодические развороты, наблюдаемые в Дополнительном файле 1:фильмы S5 и S6, а также на рис. 2.

Рассмотрим периодическое решение уравнения f ( т _X ) = f _X . Как видно из рис. 4, t _X выражается как t _X = n Т _м +0,5 Δ т _p = n Т _м +0,5 ( Т _м - Δ т _n ) с использованием целого числа n =0, ± 1, ± 2, ⋯, что далее читается как

Подставляя уравнение. (10) в уравнение. (2) для n =0, что

поясняя, что метод FM-DEP определяет частоту кроссовера, если время длительности Δ т _n от выхода микроэлектрода до разворота можно точно измерить.

Сравнение частот кроссовера одиночного MLV, определенного на FM- и AC-DEP

Мы исследовали экспериментальную точность уравнения. (11). Экспериментально биологические клетки часто необходимо диспергировать в электролите. Однако для MLV допускается использование деионизированной воды в процессе подготовки регидратации и разбавления. Поэтому мы использовали бессолевую суспензию MLV для сравнения частот кроссовера, определенных как для AC-, так и для FM-DEP.

Диэлектрофоретические развороты целевой MLV индуцировались FM-волной в диапазоне 10 кГц ≤ f ( т ) ≤ 50 кГц (т. Е. f _c =30 кГц и Δ е =20 кГц) с настройкой f _м =0,1 Гц, и соответственно FM-DEP имеет период 10 с. In the experiments, it takes less than 30 s to observe a few U-turns of the targeted MLV from leaving to approaching microelectrodes. From the trajectory, we obtained the mean leaving time that \(\overline {\Delta t_{n}}=5.8\pm 0.2\) s. Because the WBL condition applies to the present experiment satisfying that f _м /Δ е /f _м , f _, m /f ( т )<10 ⁻⁵ , the crossover frequency was evaluated to be f _X =35±1 kHz from substituting \(\overline {\Delta t_{n}}=5.8\pm 0.2\) s into Eq. (11).

For comparison, we made use of the programmable manipulator in the AC-DEP method that tries to evaluate the crossover frequency of the same targeted MLV to which the sinusoidal electric field with a frequency in the range of 30 to 100 kHz was applied via the electrode needle pair for inducing the AC-DEP. Because the programmable manipulator carries the electrode needle pair at a constant speed in one direction, we can measure the dielectrophoretic force similarly to the laser-trapping experiments [39]. Attaching the MLV on an electrode tip that undergoes uniform linear motion, not only the AC-DEP force but also the hydrodynamic force caused by the one-dimensional motion are exerted on the MLV. With the gradual increase of electrode velocity, F _DEP eventually becomes smaller than the hydrodynamic force. As a result, the MLV initially attached to the moving electrode, owing to the DEP attraction, is desorbed by the hydrodynamic force. Defining the critical value, v _c , by the maximum velocity value of the microelectrode pair prior to the desorption, the force balance equation between the DEP and hydrodynamic forces reads [39]

где F _DEP (f _AC )e ≡<F _DEP> with the unit vector e defined by \(\boldsymbol {e}=\nabla {\boldsymbol {A}}^{2}_{\text {RMS}}/|\nabla {\boldsymbol {A}}^{2}_{\text {RMS}}|\), η the water viscosity at 25 °C and 2R the diameter of the MLV.

Additional file 1:Movies S7 and S8 demonstrates the force measurement using the above AC-DEP method at the applied frequency of f _AC =60 kHz. In Additional file 1:Movie S7, the velocity of the electrode pair controlled by the programmed manipulator is 110 μ m/s, which is lower than v _c ; therefore, the MLV remains attached to one part of the electrode pair owing to the dielectrophoretic attraction. Additional file 1:Movie S8, on the other hand, shows the higher electrode speed of 120 μ m/s, under which the dielectrophoretic force becomes smaller than the hydrodynamic force that is exerted on the MLV, thereby desorbing the MLV from the electrode. Accordingly, v _c is evaluated to be 110 μ m/s ≤v _c ≤ 120 μ m/s, and we can calculate F _DEP (60 kHz) using Eq. (12).

We can determine f _X from the experimental results of F _DEP at various external frequencies. Figure 5 shows the frequency dependence of F _DEP , indicating that the DEP force experienced by the MLVs was reduced by lowering the applied frequency. It is found from Eqs. (6) and (7) that the fitting function of F _DEP (f _AC ) can be expressed as

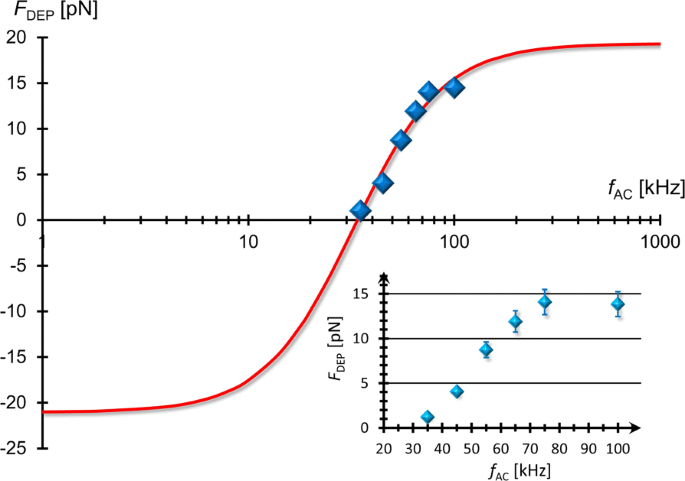
Frequency dependence of F _DEP . The FM-DEP force (F _DEP ) as a function of external frequency (f _AC ) of applied AC field where F _DEP has been evaluated from Eq. (12), the balance equation between the FM-DEP and hydrodynamic forces exerted on a single MLV. It can be seen that F _DEP is increased and saturated as f _AC is higher, reflecting a typical behavior of the relaxation spectrum of the real CM factor. The solid line represents the best-fit result of Eq. (13)

implying that

Equation (13) is depicted by the solid line in Fig. 5 that has been fitted to the experimental data using the best-fit results of three parameters:L =−21.02 pN, H =19.03 pN, and τ =4.9 μ с. Substituting these results into Eq. (14), we evaluate that f _X =34.15 kHz, which coincides with the result of f _X =35±1 kHz evaluated from the FM-DEP method. The FM-DEP method is thus validated in terms of the consistency with the direct force measurement using the AC-DEP method.

Conductivity Dependencies of the Crossover Frequencies for Biological Cells

Let us return to the dielectrophoretic U-turns of biological cells mentioned in Fig. 2 to assess the practical reliability of the crossover frequencies when the FM-DEP method is applied to cell suspensions. Recently, an elaborate theory [40] has investigated, in more detail than before, the relationship between the homogeneous sphere model (see Fig. 3) and the single-shell model where the inner structure of cell is represented by a smeared-out cytoplasm surrounded by a membrane. As a result, the relation between f _X and the suspension conductivity σ _out has been formulated using radius R of a cell, membrane capacitance C _м , and cytoplasmic conductivity σ _cyt [40]:

где f _{X 0} is the extrapolated value to the crossover frequency at σ =0 mS/m and will be treated as a fitting parameter herein. The elaborate treatment adds the squared term, the second term on the right hand side of Eq. (15), to the conventional linear relation which has mainly been used for evaluating C _м from f _X [40–45]. Theoretically, it has still been claimed [40] that Eq. (15) is valid within a lower range of σ _out such that σ _out <10 mS/m; however, it should be better to include the squared term in the evaluation of C _м , considering that our range of σ _out is relatively high compared with previous results in the range of 10 mS/m ≤σ _out ≤ 100 mS/m [40–45]. Hence, we determined σ _cyt as well as C _м from fitting Eq. (15) to the experimental results of f _X as an increasing function of σ _out .

There are three kinds of biological cell used:TL and BL cells of human leukemia and RB cells of three human volunteers. In all the experiments using any species of cell, the conductivities were within the range of 60 to 160 mS/m, and the modulation frequency was set to be 0.25 Hz. Regarding the instantaneous frequency, most of the experiments adopted the range from 100 to 1.5 MHz (i.e., f _c =800 kHz and Δ е =700 kHz); exceptionally for leukemia cells, the frequency range was extended to 50 kHz ≤f ( т )≤1550 kHz (i.e., f _c =800 kHz and Δ е X =750 kHz) in the conductivity range of 60 mS/m≤σ ≤80 mS/cm because f _X in this σ -range has been found to be lower than 100 kHz, and we were unable to observe the DEP U-turns in the range of 100 kHz ≤f ( т )≤1500 kHz. Both of these frequency sets satisfy the WBL condition of Δ е /f _м , f ( т )/f _м <10 ⁻⁵ as before.

Each time we measured the leaving times of cells dispersed in a suspension, we looked for an appropriate spot at which a few cells having a similar size could simultaneously experience the FM-DEP above the substrate, and the microelectrode tips were placed at the measurable position using the micromanipulator. We continued such scanning inside the cell suspensions until the FM-DEP trajectories of 10 cells were collected in total at a couple of appropriate positions. For each kind of cell, the measurement of 10 cells was repeated twice using different drops of the same cell suspension. As mentioned, it is indispensable for the implementation of the FM-DEP measurement at each spot to suppress the electrically induced solvent flows as much as possible. Hence, we traced only two cycles of the U-turn path so that the duration time of applying the electric field could be adjusted to be less than 10 s, and, correspondingly, the leaving time of each cell is given as the average of each trajectory, including the two U-turns. The mean leaving time \(\overline {\Delta t_{n}}\) of each cell suspension is thus obtained from averaging the leaving times of 20 cells. Particularly for human RB cells, we further averaged three sets of the mean crossover frequencies obtained for three RB cell suspensions of three human beings, supposing that cells of the same species are similar in C _м и σ _cyt as well as in R . The two-step averaging of Δ т _n will be denoted by \(\left <\overline {\Delta t_{n}}\right>\). Substituting into Eq. (10) the experimental data of either \(\overline {\Delta t_{n}}\) or \(\left <\overline {\Delta t_{n}}\right>\), the mean crossover frequency <f _X > was obtained.

Figure 6 shows the σ _out -dependencies of <f _X > measured for the above three kinds of biological cells using the FM-DEP method. The solid lines in Fig. 6 depict the best-fit results of Eq. (15). We evaluated C _м и σ _cyt from the best fitting of Eq. (15) into which the observed radii (R _obs ) were inserted. Table 1 lists the fitting results of C _м и σ _cyt , where we used the observed radii of 10 μ m ≤ 2R _obs ≤ 15 μ m for TL and BL cells, and 7.5 μ m ≤ 2R _obs ≤ 10 μ m for RB cells in evaluating C _м . It is to be noted from Table 1 that different species have different membrane capacitances, which are in good agreement with those reported in the literature [40–47]; the C _м values of RB cells with stationary whole blood samples from normal (healthy) donors are in excellent agreement with our value [46, 47], but are substantially higher than those of washed RB cells in isotonic buffered saline as noted in [47]. The best-fit results simultaneously provided cytoplasmic conductivities, which were consistently similar as seen from Table 1, but were slightly lower than the range of previous reports that 0.2 S/m ≤σ _cyt ≤1 S/m [40, 45, 48–51]. These results support that the FM-DEP method retains the practical reliability needed for the treatment of living cells.

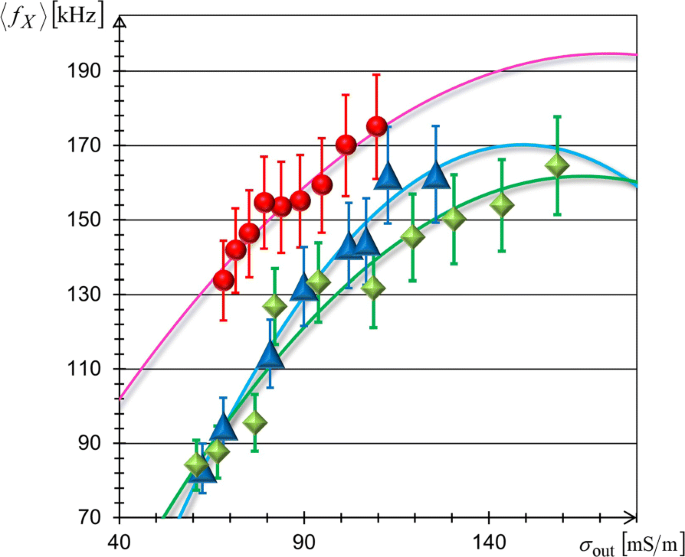
Conductivity dependences of crossover frequencies. Mean crossover frequency, <f _X >, of TL cells (blue triangles), BL cells (green diamonds), and RB cells (red circles) varying with increase of solution conductivity σ _out . The best-fit results of Eq. (15) are delineated by the solid lines

Выводы

Our theoretical treatment of the FM-DEP has mainly focused on the WBL condition. In this limit, we have proved theoretically that the direction of the FM-DEP force switches each time when the instantaneous frequency of the FM wave traverses the crossover frequency, thereby implying the periodic U-turns of micro/nanoparticles that undergo the FM-DEP. Two kinds of experiment have demonstrated the accuracy and reliability of f _X obtained from the observed trajectories of MLVs and cells using our formulation of the FM-DEP (Eqs. (9) and (11)):While the f _X evaluated from the FM-DEP of a single MLV coincides with that obtained from the force measurement of the same MLV experiencing AC-DEP, the conductivity dependencies of f _X provide the membrane capacitances of various cells that are in close agreement with the literature values. In other words, it has been validated theoretically and experimentally that the FM-DEP in the WBL limit can be mimicked by the time-varying AC-DEP induced by the AC wave with its frequency changing continuously according to the periodic function of f ( т ). The simple view applies to other electrokinetics, including the twDEP and the electrorotation by applying the FM wave that has the spatial dependence of the phase as well as the magnitude. The AC- and FM-DEPs are associated with the real part of the dielectric spectra (or the CM factor), whereas the electrokinetics due to the spatial gradient of the phase reflect the imaginary part of the CM factor as mentioned before. Therefore, the application of the FM wave to either twDEP or electrorotation will be required for completing the dielectric characterization (the dielectric spectroscopy, in general) using the electrokinetics.

We have treated microparticles such as MLVs and cells for the precise tracking of particle trajectories. In these experiments, sedimented particles as well as floating ones have been observed; we need to increase the magnitude of electric field for inducing the DEP of the sedimented particles which are likely to be aggregated. Accordingly, we have used the plug-in system for applying the FM wave to a targeted particle floating above the substrate.

It is promising to further develop the FM-DEP method for smaller particles with their sizes of submicron to nanoscale, such as dispersed carbon nanotubes, thereby opening up the possibility of real-time spectroscopy using the FM-DEP as described below. When we apply the FM wave to the smaller colloids using the on-chip systems whose electrode configuration is designed to create a constant gradient of the applied electric field, the time-varying velocity vector v ( т ) of the FM-DEP caused by the time dependence of the FM-DEP force is ascribed to the variation in χ (f ) (or the real part of the CM factor):it is found from Eqs. (9) and (12) that

Hence, measuring the velocity vector v ( т ) of a submicron to nanoparticle could provide the frequency dependence of the real part of the CM factor directly, which would be nothing but the electrokinetic FM spectroscopy.

Сокращения

AC:

Alternating current

BL:

B cell leukemia

CM:

Clausius-Mossotti

DEP:

Dielectrophoresis

DOPC:

1,2-Dioleoyl-sn-glycero-3-phosphatidylcholine

FM:

Frequency modulated

MLV:

Multilamellar vesicle

RB:

Red blood

RMS:

Root mean squared

TL:

T cell leukemia

twDEP:

Traveling wave dielectrophoresis

WBL:

Wide band limit