Измерение частоты и фазы

Важной электрической величиной, не имеющей эквивалента в цепях постоянного тока, является частота . .

Измерение частоты очень важно во многих приложениях переменного тока, особенно в энергосистемах переменного тока, предназначенных для эффективной работы только на одной частоте и только на одной частоте.

Если переменный ток генерируется электромеханическим генератором переменного тока, частота будет прямо пропорциональна скорости вала машины, а частоту можно измерить, просто измерив скорость вала.

Однако, если необходимо измерить частоту на некотором расстоянии от генератора, потребуются другие средства измерения.

Метод измерения частоты

Использование принципа механического резонанса

Один простой, но грубый метод измерения частоты в энергосистемах использует принцип механического резонанса. Каждому физическому объекту, обладающему свойством упругости (упругости), присуща собственная частота, с которой он предпочитает колебаться.

Камертон является отличным примером этого:ударьте по нему один раз, и он продолжит вибрировать с тональностью, соответствующей его длине. Более длинные камертоны имеют более низкие резонансные частоты:их тон будет ниже на музыкальной шкале, чем более короткие вилки.

Представьте себе ряд камертонов постепенно увеличивающегося размера, расположенных бок о бок. Все они установлены на общем основании, и это основание вибрирует с частотой измеряемого переменного напряжения (или тока) с помощью электромагнита.

Какой бы камертон по резонансной частоте ближе всего к частоте этой вибрации, он будет трястись сильнее всего (или громче всего). Если бы зубцы вилки были достаточно хрупкими, мы могли бы видеть относительное движение каждого по длине размытия, которое мы увидели бы, когда осматривали бы каждый из них с точки зрения торца.

Итак, сделайте набор «камертонов» из полосы листового металла, вырезанной по образцу, похожему на грабли, и у вас будет вибрирующий язычок частотомер:

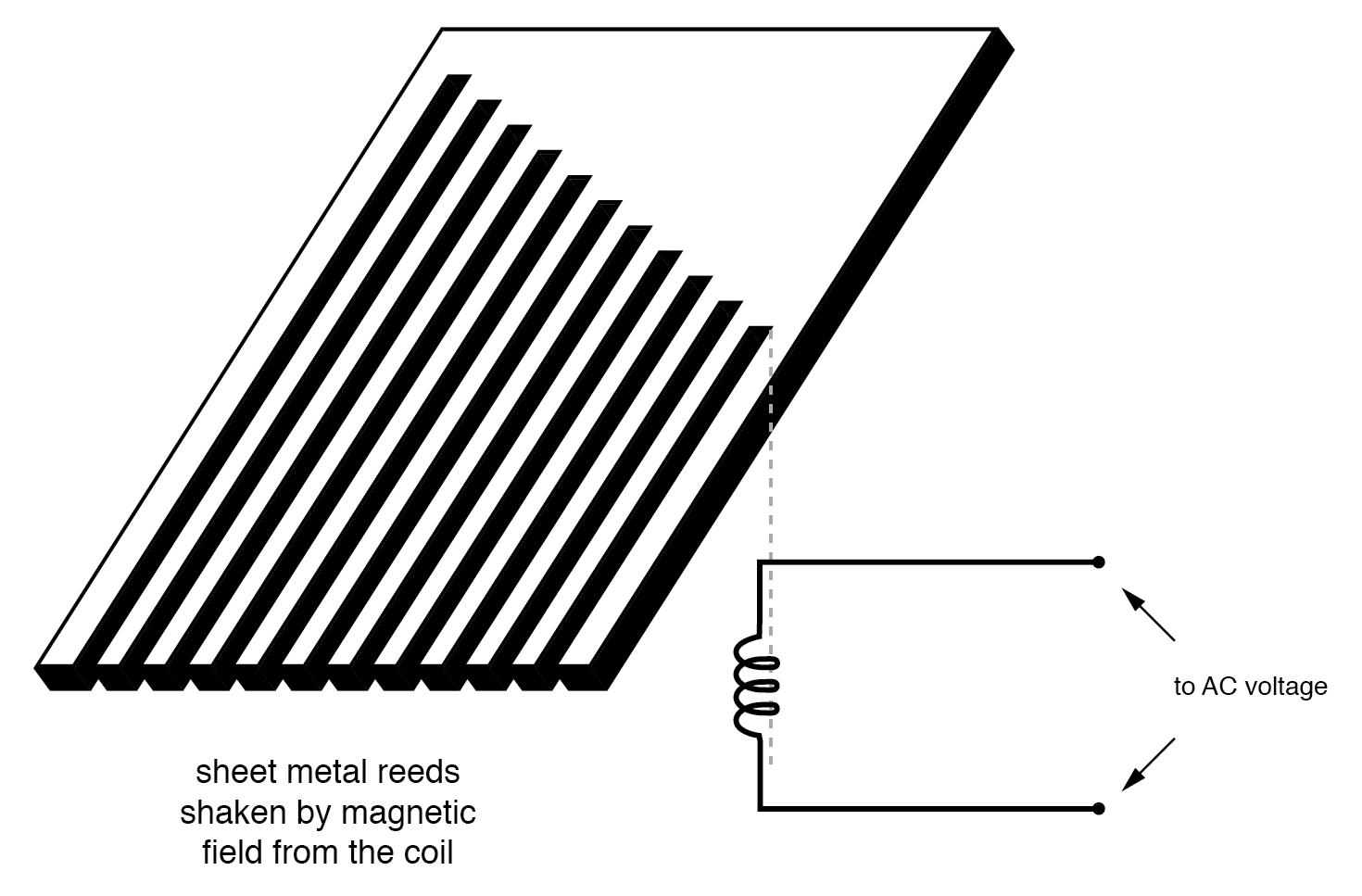
Схема частотомера вибрирующего язычка.

Пользователь этого измерителя видит концы всех этих язычков разной длины, поскольку они все вместе встряхиваются с частотой приложенного переменного напряжения к катушке. Самый близкий по резонансной частоте к приложенному переменному току будет вибрировать сильнее всего, примерно так:

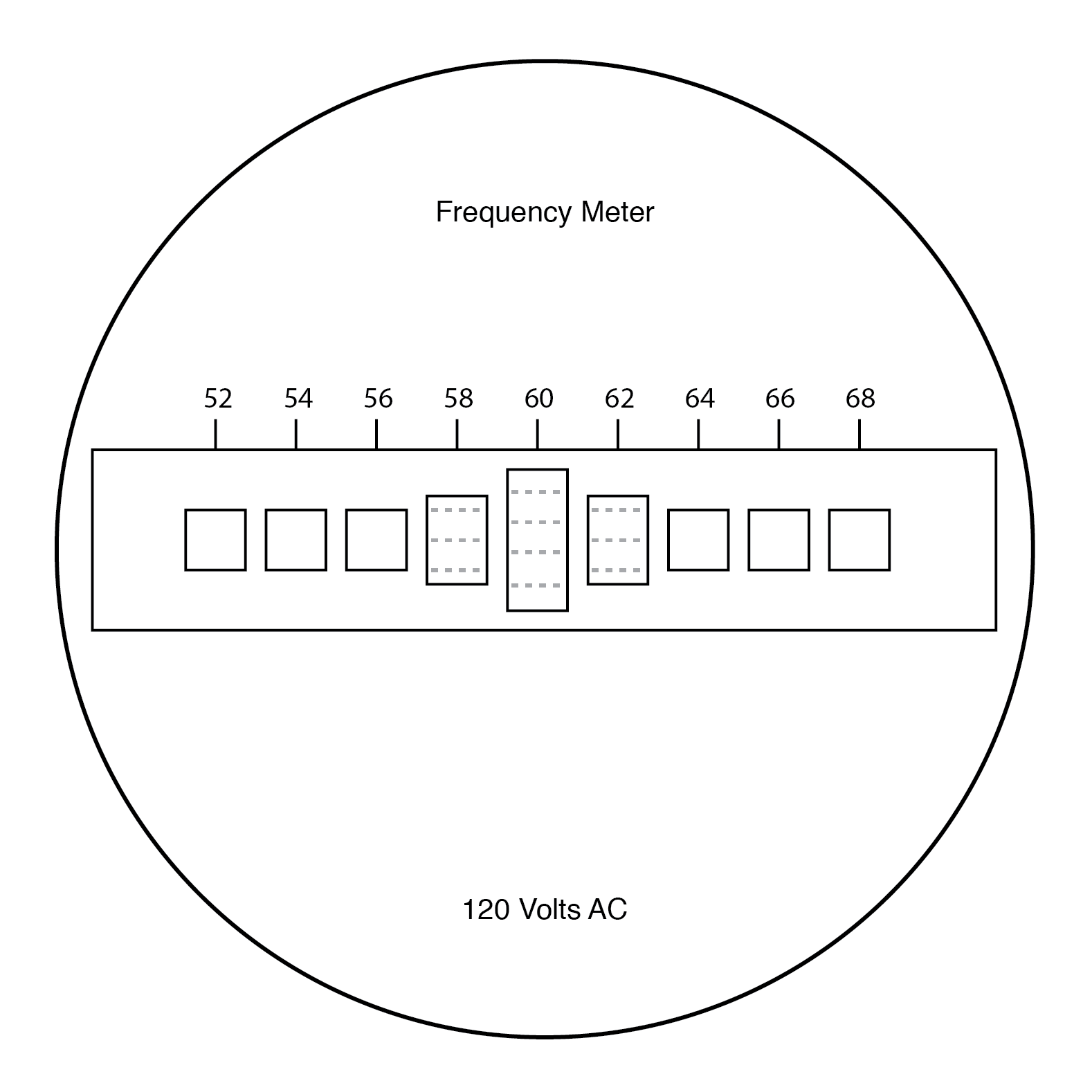
Передняя панель частотомера с вибрирующим язычком.

Вибрационные язычковые измерители, разумеется, не являются точными приборами, но они очень просты и, следовательно, их легко изготовить, чтобы они были прочными. Их часто можно найти на небольших генераторных установках с приводом от двигателя, чтобы установить частоту вращения двигателя, близкую к 60 (50 в Европе) герц.

Использование формы цепи резервуара

Герконовые счетчики неточны, но принцип их действия - нет. Вместо механического резонанса мы можем заменить электрический резонанс и сконструировать частотомер, использующий индуктор и конденсатор в виде цепи резервуара (параллельные индуктор и конденсатор). См. Рисунок ниже.

Один или оба компонента сделаны регулируемыми, и в цепь помещается измеритель, который показывает максимальную амплитуду напряжения на двух компонентах.

Ручка (ручки) регулировки откалиброваны так, чтобы показывать резонансную частоту для любой заданной настройки, и частота считывается с них после того, как устройство было настроено на максимальное показание на измерителе.

По сути, это настраиваемая схема фильтра, которая настраивается и затем считывается аналогично мостовой схеме (которая должна быть сбалансирована для «нулевого» состояния, а затем считана).

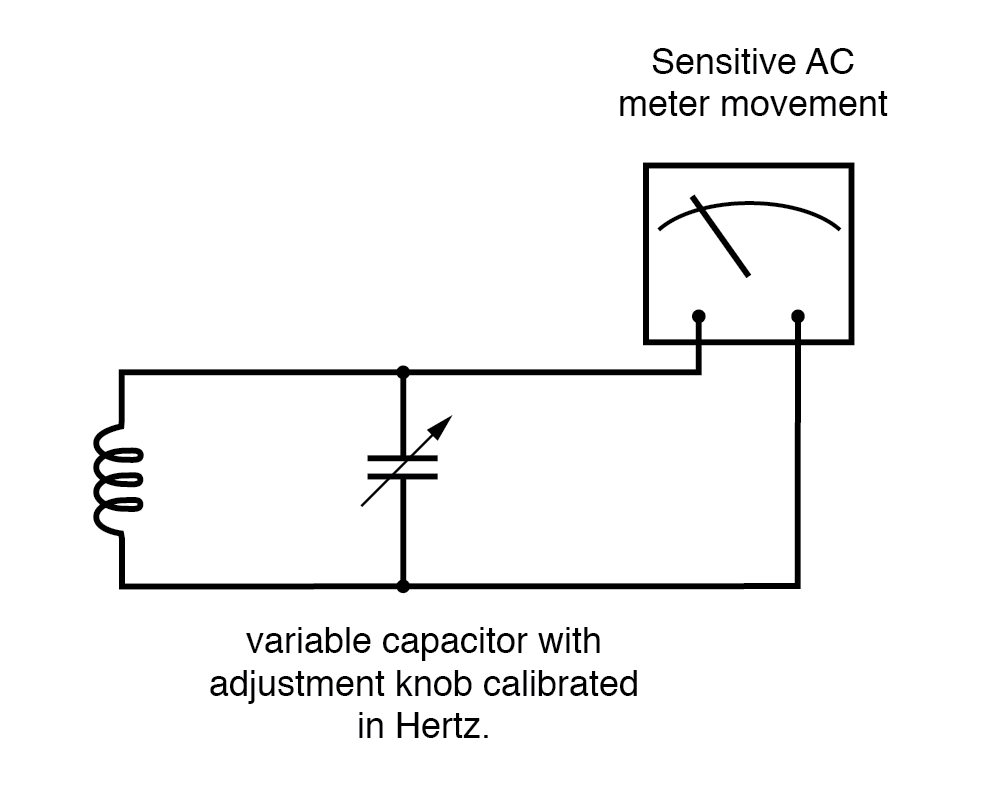
Резонансный частотомер "достигает пика", когда резонансная частота L-C настроена на тестовую частоту.

Этот метод популярен среди радиолюбителей (по крайней мере, так было до появления недорогих цифровых частотных инструментов, называемых счетчиками ), особенно потому, что не требует прямого подключения к цепи.

Пока катушка индуктивности и / или конденсатор могут улавливать достаточное количество паразитного поля (магнитного или электрического, соответственно) от тестируемой цепи, чтобы измеритель показывал, он будет работать.

Что касается частоты, как и в других типах электрических измерений, наиболее точными средствами измерения обычно являются те, где неизвестная величина сравнивается с известным эталоном . , основной инструмент не делает ничего, кроме индикации, когда две величины равны друг другу.

Это основной принцип, лежащий в основе мостовой схемы постоянного тока (Уитстона), и это надежный метрологический принцип, применяемый во всех науках. Если у нас есть доступ к точному стандарту частоты (источник переменного напряжения, очень точно поддерживающий одну частоту), для сравнения, измерение неизвестной частоты должно быть относительно простым.

Использование кристалла кварца

Для этого стандарта частоты мы снова обращаем внимание на камертон или, по крайней мере, на его более современный вариант, называемый кварцевым кристаллом . .

Кварц - это природный минерал, обладающий очень интересным свойством, называемым пьезоэлектричеством . . Пьезоэлектрические материалы создают напряжение по всей своей длине при физическом напряжении и будут физически деформироваться, когда по всей их длине будет приложено внешнее напряжение.

Эта деформация в большинстве случаев очень и очень небольшая, но она существует.

Кварцевая порода эластична (упруга) в том небольшом диапазоне изгиба, который может вызвать внешнее напряжение, а это означает, что она будет иметь собственную механическую резонансную частоту, которая может проявляться как сигнал электрического напряжения.

Другими словами, если удар по кварцевой микросхеме, он будет «звенеть» со своей собственной уникальной частотой, определяемой длиной чипа, и это резонансное колебание создаст эквивалентное напряжение на нескольких точках кварцевого чипа, которые можно отстукивать. в проводами, прикрепленными к поверхности микросхемы.

И наоборот, кварцевый чип будет больше всего вибрировать, когда он «возбуждается» приложенным напряжением переменного тока точно нужной частоты, точно так же, как язычки в частотомере с вибрирующим язычком.

Кусочки кварцевого камня могут быть точно разрезаны для достижения желаемых резонансных частот, и этот чип надежно закреплен внутри защитной оболочки с проводами, идущими для подключения к внешней электрической цепи.

В таком виде полученное устройство называется просто кристаллом . (или иногда « xtal »). Схематический символ показан на рисунке ниже.

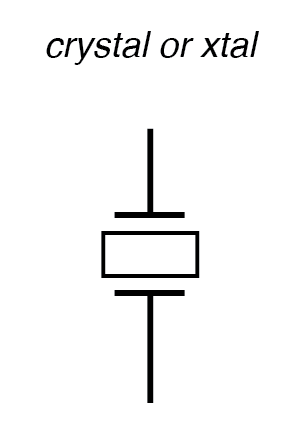
Символ схемы кристалла (элемент, определяющий частоту) .

Электрически этот кварцевый чип эквивалентен последовательному LC-резонансному контуру. (Рисунок ниже) Диэлектрические свойства кварца вносят дополнительный емкостной элемент в эквивалентную схему.

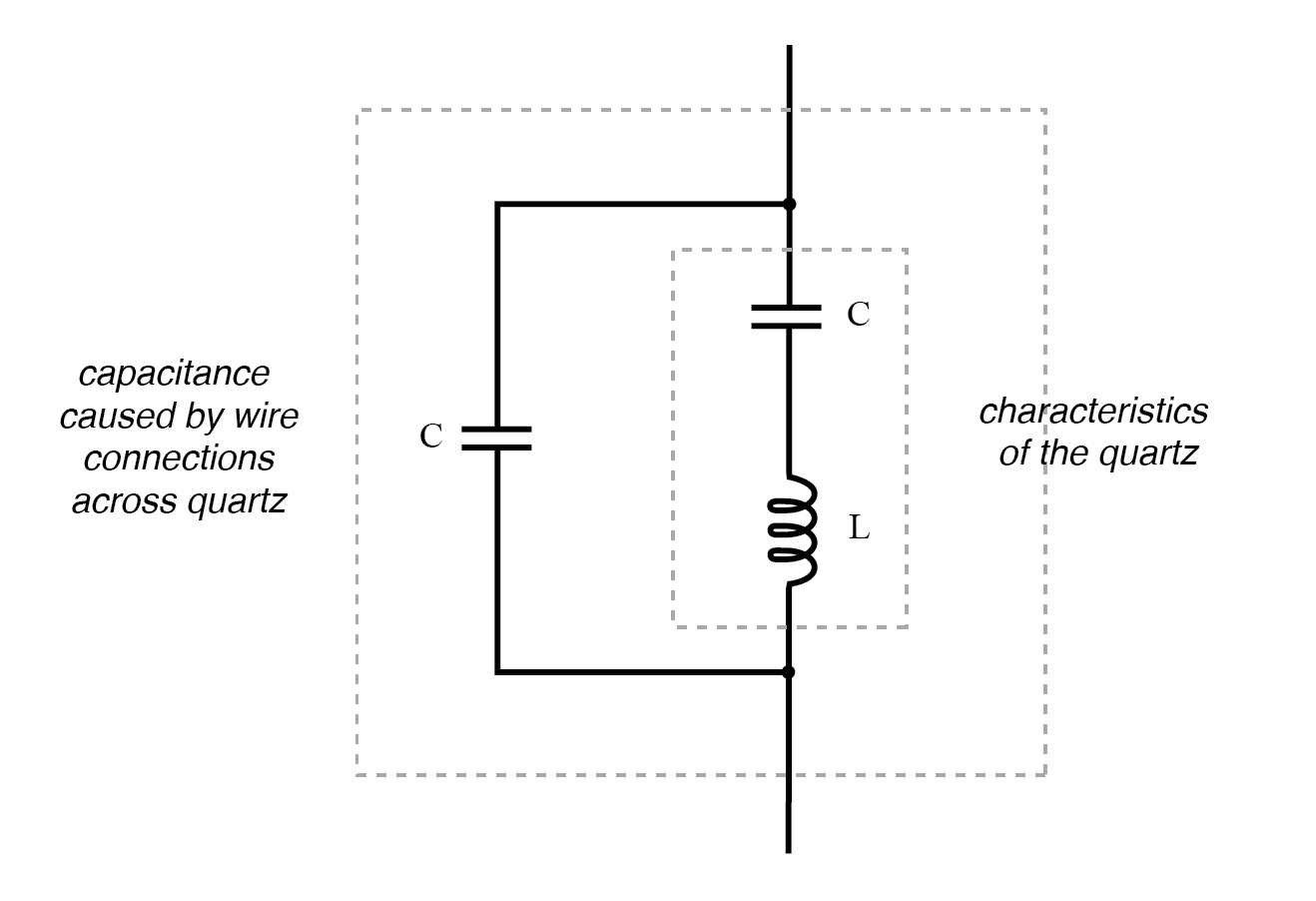
Эквивалентная схема кристалла кварца.

«Емкость» и «индуктивность», показанные последовательно, являются просто электрическими эквивалентами механических резонансных свойств кварца:они не существуют в виде дискретных компонентов внутри кристалла. Емкость, показанная параллельно из-за проводных соединений через диэлектрический (изолирующий) кварцевый корпус, является реальной и влияет на резонансный отклик всей системы.

Здесь нет необходимости в полном обсуждении динамики кристалла, но необходимо понимать, что кристаллы эквивалентны резонансному контуру и как его можно использовать в контуре генератора для получения выходного напряжения со стабильной известной частотой.

Кристаллы, как резонансные элементы, обычно имеют гораздо более высокую добротность ( качество ) значений, чем резервуарные цепи, построенные из катушек индуктивности и конденсаторов, в основном из-за относительного отсутствия паразитного сопротивления, что делает их резонансные частоты очень определенными и точными.

Поскольку резонансная частота зависит исключительно от физических свойств кварца (механически очень стабильного вещества), изменение резонансной частоты с течением времени для кристалла кварца очень и очень мало. Вот как кварцевый механизм часы получают свою высокую точность:с помощью электронного генератора, стабилизированного резонансным действием кварцевого кристалла.

Однако для лабораторных приложений может потребоваться еще большая стабильность частоты. Для этого рассматриваемый кристалл может быть помещен в среду со стабилизированной температурой (обычно в печь), что устраняет частотные ошибки из-за теплового расширения и сжатия кварца.

Что же касается эталона частоты, то на данный момент ничего не обнаружено выше точности одиночного резонирующего атома. Это принцип так называемых атомных часов . , в котором используется взвешенный в вакууме атом ртути (или цезия), возбужденный внешней энергией для резонанса на собственной уникальной частоте.

Результирующая частота определяется как радиоволновой сигнал, который составляет основу самых точных часов, известных человечеству. Национальные лаборатории стандартизации по всему миру поддерживают некоторые из этих сверхточных часов и передают частотные сигналы, основанные на колебаниях этих атомов, чтобы ученые и техники могли настраиваться и использовать их для калибровки частоты.

Практическая часть

Теперь мы переходим к практической части:когда у нас есть исходный код точной частоты, как мы можем сравнить ее с неизвестной частотой, чтобы получить измерение?

Один из способов - использовать ЭЛТ в качестве устройства для сравнения частот. Электронно-лучевые трубки обычно имеют средства отклонения электронного пучка как по горизонтальной, так и по вертикальной оси.

Если металлические пластины используются для электростатического отклонения электронов, будет пара пластин слева и справа от луча, а также пара пластин выше и ниже луча, как показано на рисунке ниже.

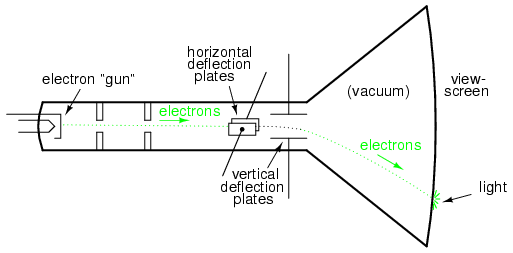
Электронно-лучевая трубка (ЭЛТ) с вертикальными и горизонтальными отклоняющими пластинами.

Если мы позволим одному сигналу переменного тока отклонять луч вверх и вниз (подключить этот источник переменного напряжения к «вертикальным» отклоняющим пластинам), а другому сигналу переменного тока отклонять луч влево и вправо (с помощью другой пары отклоняющих пластин), шаблоны будут воспроизводиться на экране ЭЛТ с указанием соотношения сторон этих двух частот переменного тока.

Эти узоры называются фигурами Лиссажу . и являются обычным средством сравнительного измерения частоты в электронике.

Если две частоты совпадают, мы получим простой рисунок на экране ЭЛТ, форма которого зависит от фазового сдвига между двумя сигналами переменного тока. Вот пример фигур Лиссажу для двух синусоидальных сигналов равной частоты, показанных на лицевой панели осциллографа (прибор для измерения напряжения переменного тока, использующий ЭЛТ в качестве «движения»).

На первом изображении изображена фигура Лиссажу, образованная двумя напряжениями переменного тока, идеально совпадающими по фазе друг с другом:

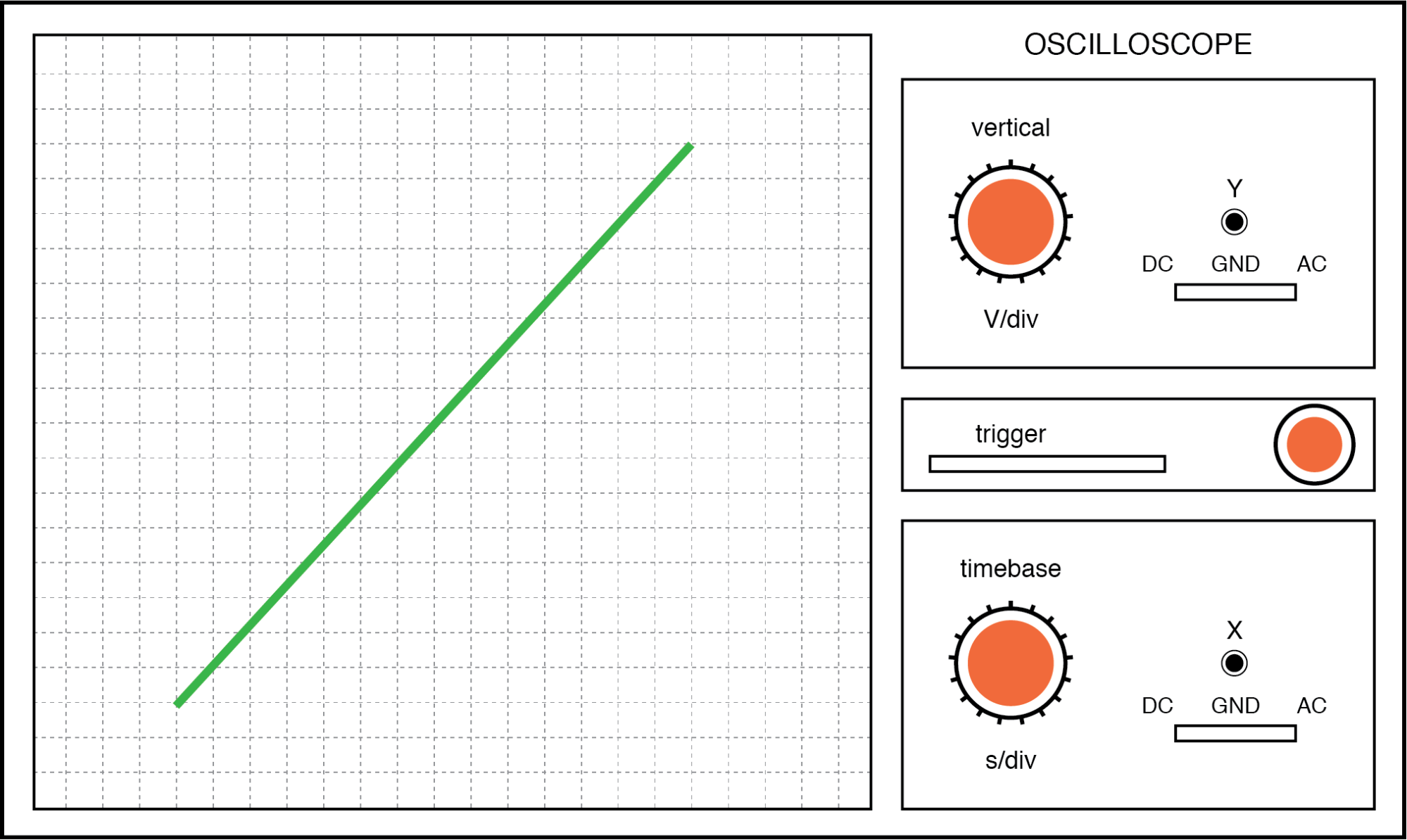
Фигура Лиссажу:та же частота, фазовый сдвиг 0 градусов.

Если два напряжения переменного тока не совпадают по фазе друг с другом, прямая линия не образуется. Скорее, фигура Лиссажу примет вид овала и станет идеально круглой, если фазовый сдвиг между двумя сигналами составляет точно 90 ° и если их амплитуды равны:

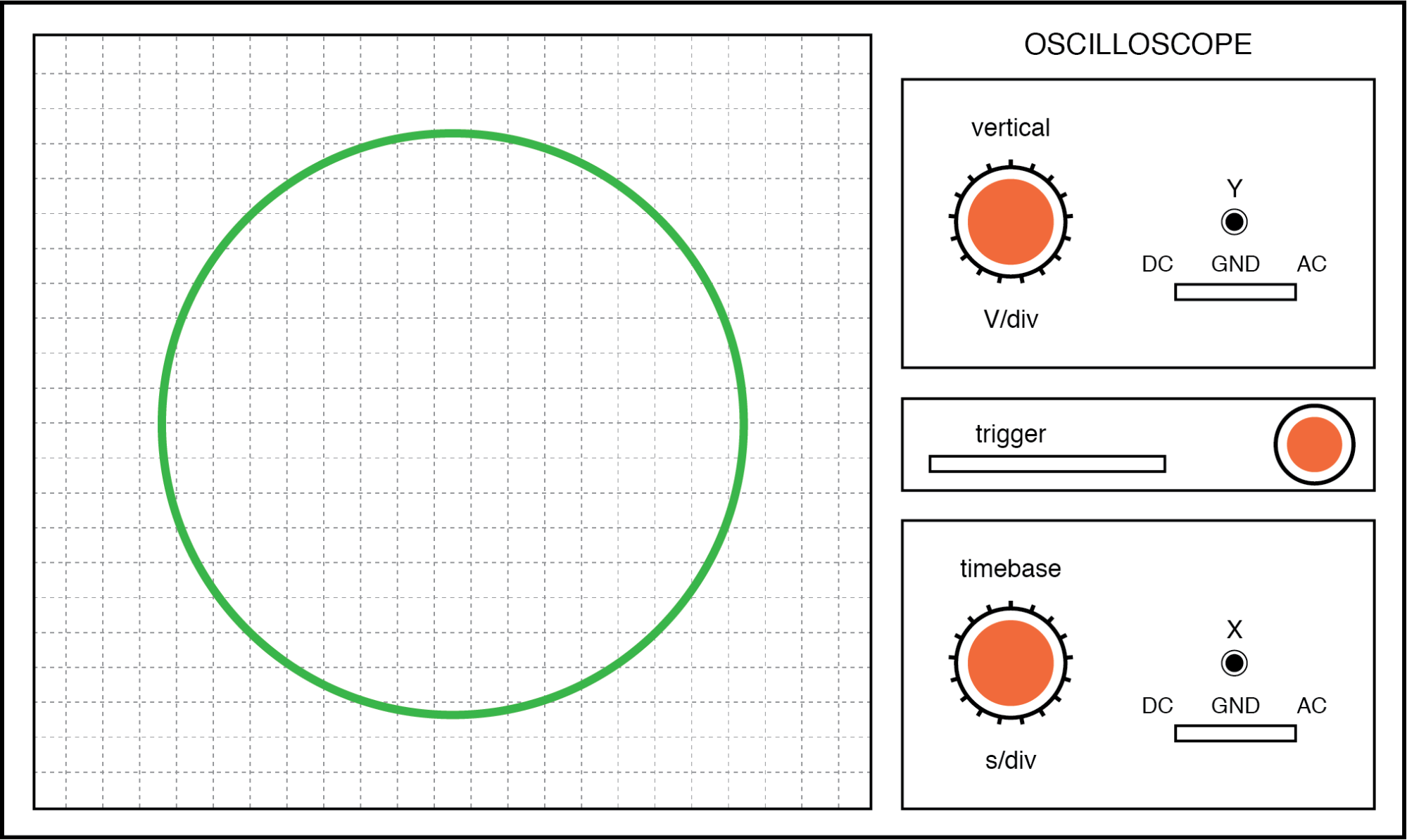
Фигура Лиссажу:та же частота, фазовый сдвиг 90 или 270 градусов.

Наконец, если два сигнала переменного тока прямо противоположны друг другу по фазе (сдвиг на 180 °), мы снова получим линию, только на этот раз она будет ориентирована в противоположном направлении:

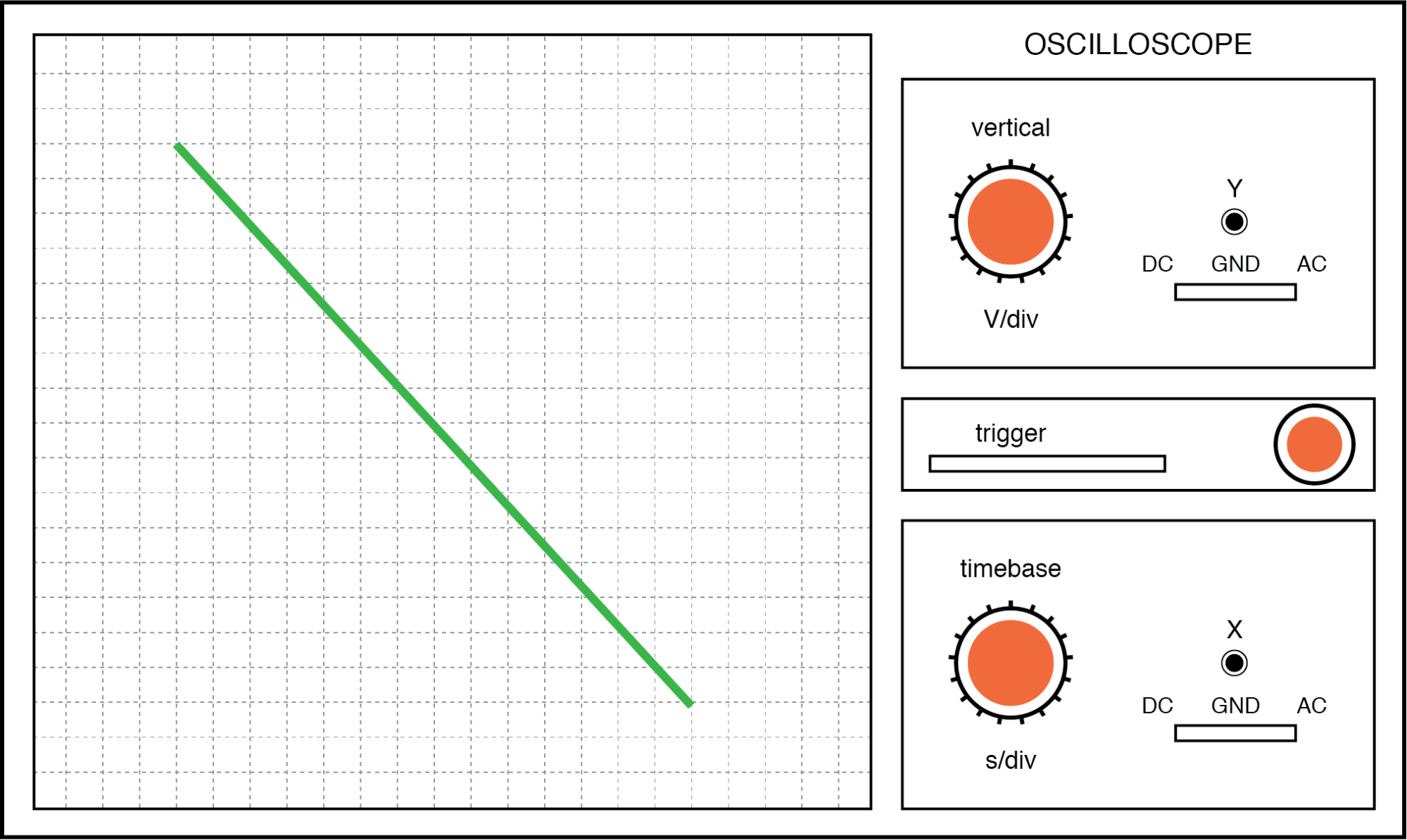
Фигура Лиссажу:та же частота, фазовый сдвиг 180 градусов.

Когда мы сталкиваемся с разными частотами сигналов, фигуры Лиссажу становятся немного сложнее. Рассмотрим следующие примеры, и им дано соотношение вертикальной и горизонтальной частоты:

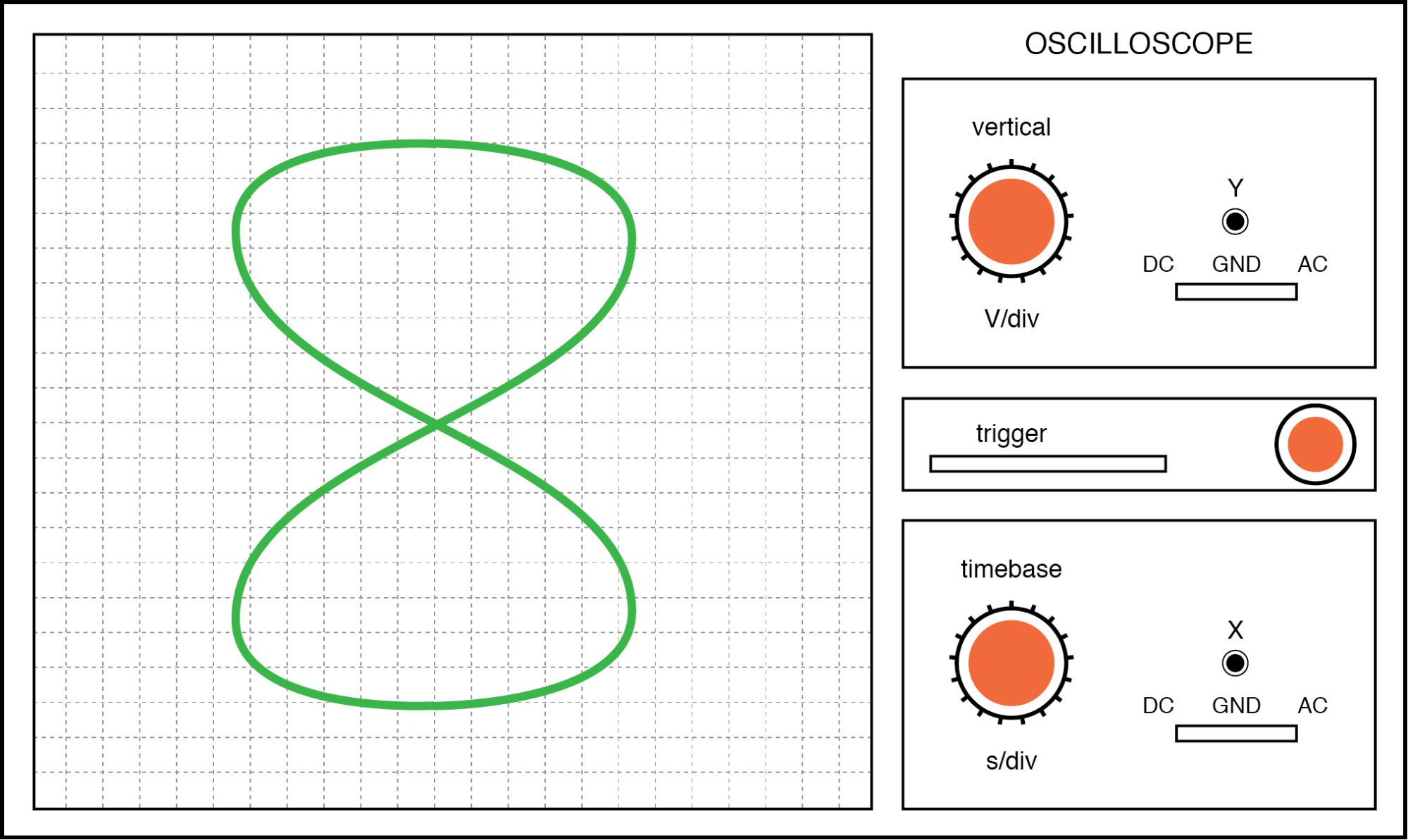
Фигура Лиссажу:горизонтальная частота в два раза больше вертикальной.

Чем сложнее соотношение горизонтальной и вертикальной частот, тем сложнее фигура Лиссажу. Рассмотрим следующую иллюстрацию соотношения частот по горизонтали и вертикали 3:1:

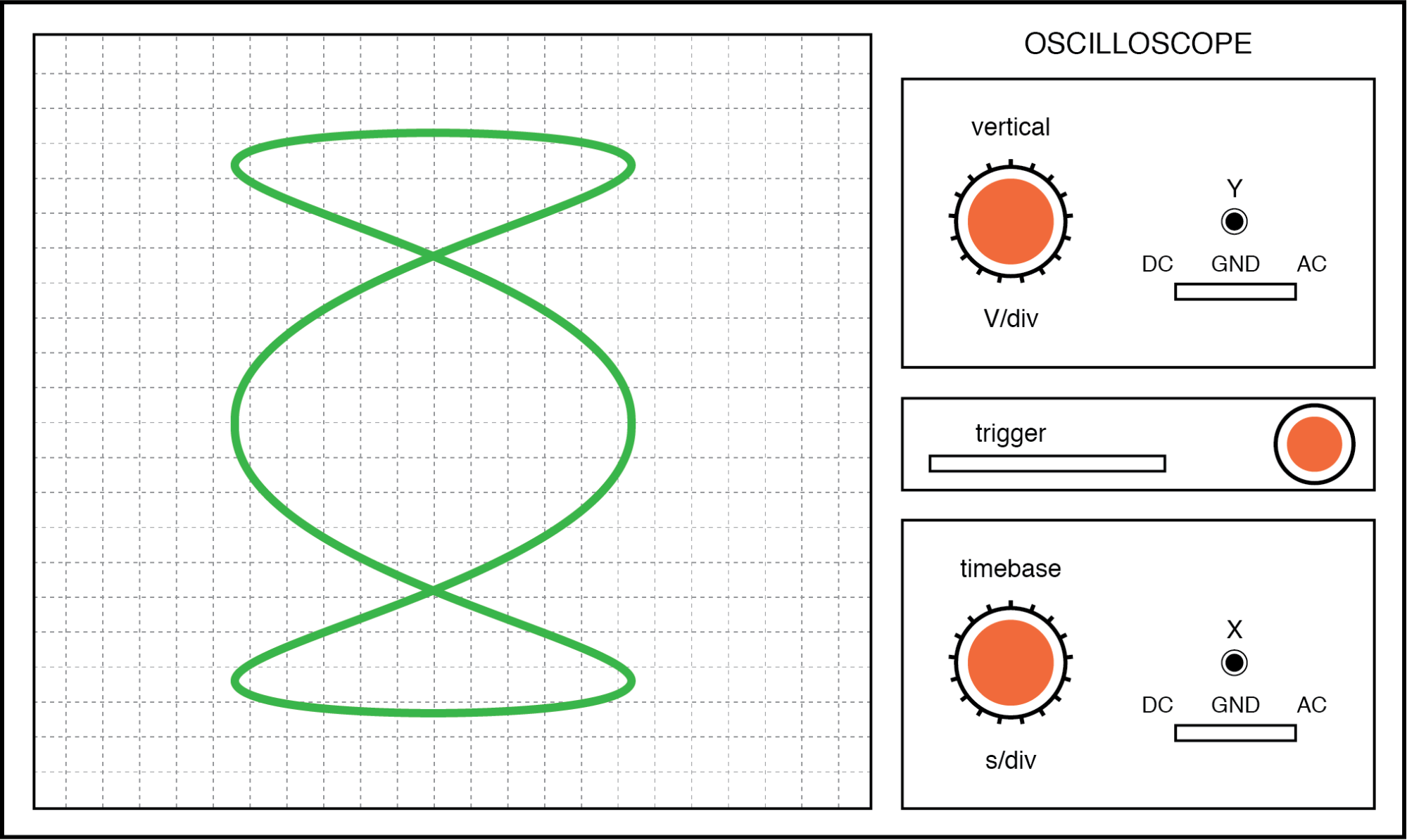
Фигура Лиссажу:горизонтальная частота в три раза больше, чем вертикальная.

. . . и соотношение частот 3:2 (по горизонтали =3, по вертикали =2) на рисунке ниже.

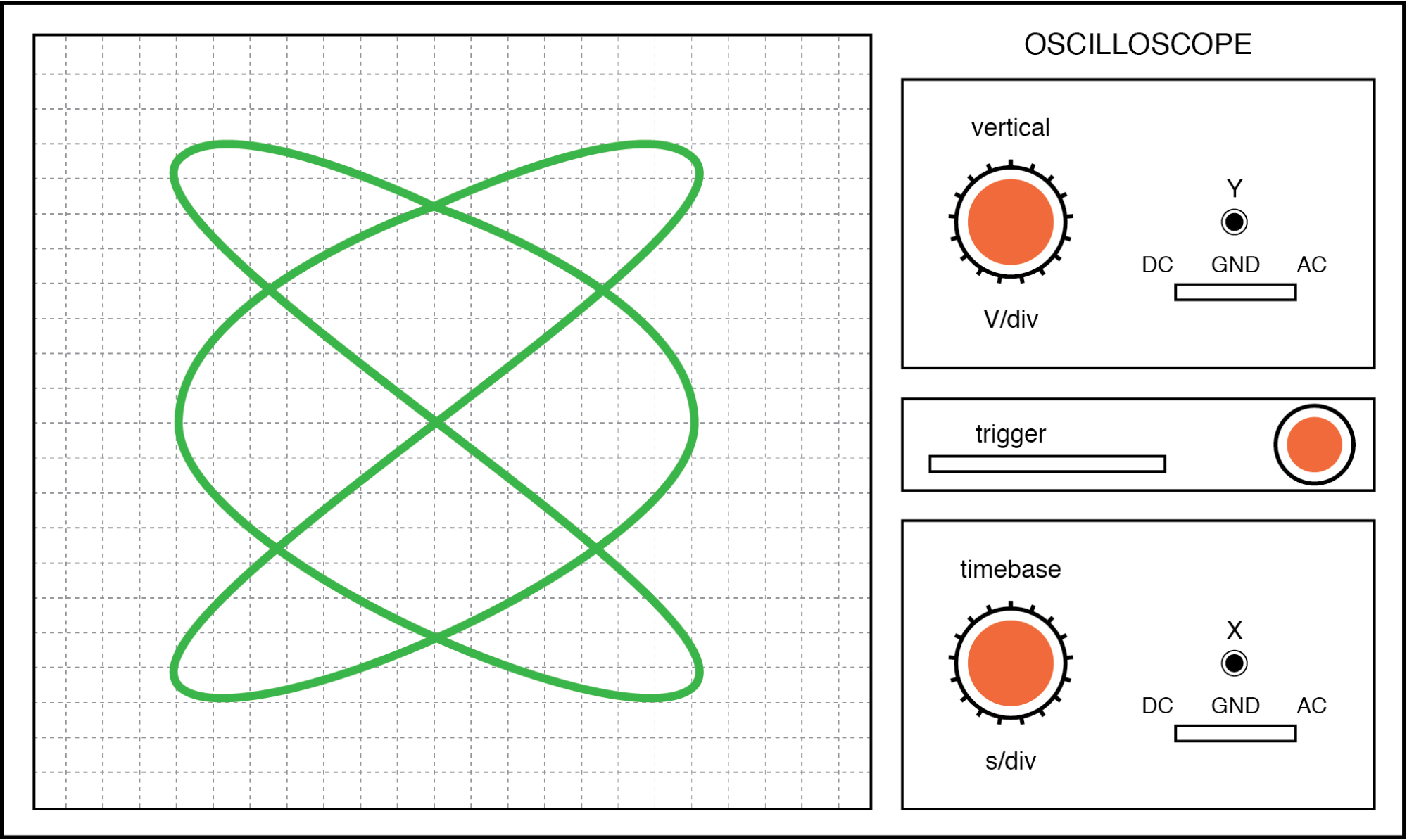
Фигура Лиссажу:соотношение частот горизонтальной и вертикальной развертки составляет 3:2.

В случаях, когда частоты двух сигналов переменного тока не совсем простое отношение друг к другу (но близко), фигура Лиссажу будет казаться «движущейся», медленно меняя ориентацию, поскольку фазовый угол между двумя формами волны колеблется между 0 ° и 180 °.

Если две частоты зафиксированы в точном целочисленном соотношении между собой, фигура Лиссажу будет стабильной на обзорном экране ЭЛТ.

Физика фигур Лиссажу ограничивает их полезность в качестве метода сравнения частот случаями, когда отношения частот являются простыми целыми числами (1:1, 1:2, 1:3, 2:3, 3:4 и т. Д.).

Несмотря на это ограничение, фигуры Лиссажу являются популярным средством сравнения частот везде, где существует доступный стандарт частоты (генератор сигналов).

ОБЗОР:

• Некоторые частотомеры работают по принципу механического резонанса, показывая частоту посредством относительных колебаний среди набора уникально настроенных «язычков», колеблющихся на измеренной частоте.
• В других частотомерах используются электрические резонансные цепи (обычно цепи LC-резервуара) для измерения частоты. Один или оба компонента могут регулироваться с помощью точно откалиброванной ручки регулировки, а чувствительный измеритель считывает максимальное напряжение или ток в точке резонанса.
• Частоту можно измерить сравнительным способом, как в случае использования ЭЛТ для создания фигур Лиссажу. Сигналы опорной частоты могут быть получены с высокой степенью точности с помощью схем генераторов, использующих кристаллы кварца в качестве резонансных устройств. Для сверхточности можно использовать эталоны сигналов атомных часов (основанные на резонансных частотах отдельных атомов).