Фаза переменного тока

Все начинает усложняться, когда нам нужно связать два или более переменного напряжения или тока, которые не совпадают друг с другом. Под «несогласованным» я подразумеваю, что две формы сигнала не синхронизированы:их пики и нулевые точки не совпадают в одни и те же моменты времени. График на рисунке ниже иллюстрирует это.

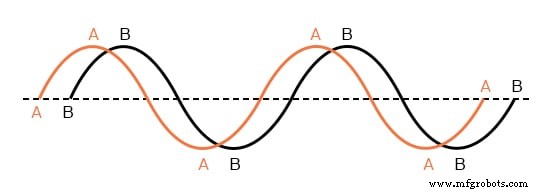
Сигналы вне фазы.

Две волны, показанные выше (A и B), имеют одинаковую амплитуду и частоту, но они не совпадают друг с другом. Технически это называется фазовым сдвигом . . Ранее мы видели, как построить «синусоидальную волну», вычислив тригонометрическую синусоидальную функцию для углов от 0 до 360 градусов, то есть полного круга.

Начальной точкой синусоидальной волны была нулевая амплитуда при нулевом градусе, прогрессирующая до полной положительной амплитуды при 90 градусах, нуля при 180 градусах, полной отрицательной при 270 градусах и возврата к начальной точке нуля при 360 градусах.

Мы можем использовать эту угловую шкалу вдоль горизонтальной оси нашего графика формы волны, чтобы выразить, насколько далеко одна волна отличается от другой:Рисунок ниже

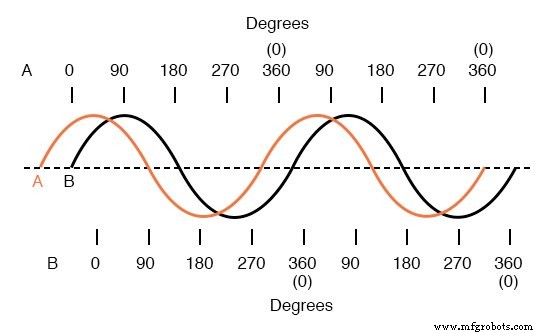
Волна A опережает волну B на 45 °

Сдвиг между этими двумя формами волны составляет около 45 градусов, причем волна «А» опережает волну «В». Выборка различных фазовых сдвигов представлена ​​на следующих графиках, чтобы лучше проиллюстрировать эту концепцию:Рисунок ниже

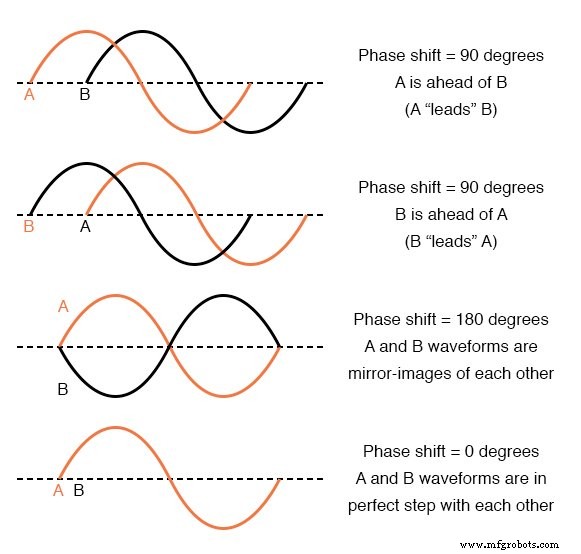
Примеры фазовых сдвигов.

Поскольку формы сигналов в приведенных выше примерах имеют одинаковую частоту, они будут отклоняться от шага на одинаковую угловую величину в каждый момент времени. По этой причине мы можем выразить фазовый сдвиг для двух или более сигналов одной и той же частоты как постоянную величину для всей волны, а не просто выражение сдвига между любыми двумя конкретными точками вдоль волн.

То есть можно с уверенностью сказать что-то вроде:«Напряжение« А »сдвинуто по фазе на 45 градусов с напряжением« В »». Какая бы форма волны ни развивалась впереди, считается, что она ведущая . а тот, кто отстает, называется отстающим .

Фазовый сдвиг, как и напряжение, всегда является измерением относительно двух вещей. На самом деле не существует такой вещи, как форма волны с абсолютным измерение фазы, потому что не существует известного универсального эталона для фазы.

Обычно при анализе цепей переменного тока форма волны напряжения источника питания используется в качестве эталона для фазы, это напряжение указано как «xxx вольт при 0 градусах». Любое другое переменное напряжение или ток в этой цепи будет иметь фазовый сдвиг, выраженный в терминах относительно этого исходного напряжения.

Это то, что делает расчеты цепей переменного тока более сложными, чем вычисления постоянного тока. При применении закона Ома и закона Кирхгофа величины переменного напряжения и тока должны отражать фазовый сдвиг, а также амплитуду. Математические операции сложения, вычитания, умножения и деления должны оперировать этими величинами фазового сдвига, а также амплитуды.

К счастью, существует математическая система величин, называемая комплексными числами . идеально подходит для этой задачи по представлению амплитуды и фазы.

Поскольку комплексные числа так важны для понимания цепей переменного тока, следующая глава будет посвящена только этому предмету.

ОБЗОР:

• Фазовый сдвиг здесь две или более формы сигналов не совпадают друг с другом.
• Величину фазового сдвига между двумя волнами можно выразить в градусах, как это определено в градусах на горизонтальной оси графика формы волны, используемой при построении тригонометрической синусоидальной функции.
• ведущий форма волны определяется как одна форма волны, которая опережает другие в своем развитии. отстающий форма волны - одна за другой. Пример:

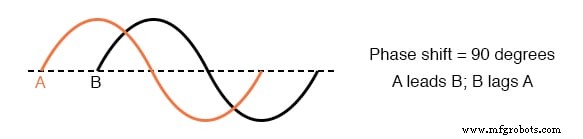
• При расчетах для анализа цепей переменного тока необходимо учитывать как амплитуду, так и фазовый сдвиг сигналов напряжения и тока, чтобы быть полностью точными. Это требует использования математической системы, называемой комплексными числами . .

СВЯЗАННЫЕ РАБОЧИЕ ТАБЛИЦЫ:

• Таблица тригонометрии для цепей переменного тока