Исследование фрикционного поведения графена на золотых подложках в наномасштабе с помощью молекулярной динамики

Фон

Графен - один из многообещающих новых материалов для применения в наноразмерной электронике среди широкого круга потенциальных приложений [1,2,3,4,5]. В реальных электронных устройствах на основе графена золото обычно используется для электрических контактов [6]. Таким образом, трение системы графен-золото играет важную роль в эффективном изготовлении и надежной работе таких графеновых устройств. Хотя графен вызвал большой интерес исследователей в области нанотрибологии из-за его превосходных механических свойств [3, 7], фрикционные свойства графена, скользящего по поверхности золота, изучены недостаточно. Пока что многие трибологические исследования графена сосредоточены на силе трения между графеном и острием сканирующего зонда [8,9,10,11,12,13,14]. Например, эксперименты по атомно-силовой микроскопии (АСМ) трения по химически модифицированному графиту показали отрицательный коэффициент трения [9]. Эксперименты с микроскопом силы трения (FFM) для многослойного графена показали, что трение увеличивается с уменьшением количества слоев графена [10, 11]. Эти явления объясняются сморщивающим эффектом графена [9,10,11]. Предполагается, что трение между чешуей графена и графитом измерялось, когда острие волочило чешуйку во время скольжения по графиту [8, 14]. Установлено, что вращательное движение, связанное с поперечным движением чешуек для пластинчатых твердых тел, приводит к увеличению трения из-за переориентации чешуек в соизмеримую конфигурацию [15]. В то же время некоторые ученые также посвятили себя изучению трения графена и / или золота с использованием других методов. Метод микровесов на кристаллах кварца (QCM) был использован для исследования смазывающей способности золота на графене [16] и трения скольжения твердой пленки ксенона на подложке графен / Ni (111) [17]. Как эксперименты QCM, так и моделирование методом молекулярной динамики (МД) показывают, что трение несоразмерного монослоя Kr по Au подчиняется закону вязкого трения [18, 19]. МД моделирования проводятся для изучения статического трения двумерных островков золота и трехмерных кластеров золота на графитовой подложке [20]. Обнаружено, что толщина ползуна может способствовать смазывающим свойствам из-за более высокой эффективной жесткости толстых кластеров. Зависимая от размера межфазная соизмеримость была также обнаружена с помощью МД-моделирования атомов ксенона на графене и подложке Au [21], что согласуется с моделированием кластеров криптона и кремния на подложке Cu [22], что может объяснить размерную зависимость статического трения. В последнее время сверхсмазка графеновых нанолент на подложке из Au (111) наблюдается при низкой температуре [23]. Kitt et al. непосредственно измерил трение графена, скользящего по SiO ₂ подложке и обнаружили, что поведение трения для монослоя и двухслойного графена нарушает закон Амонтона [24]. В целом, как чистый двумерный материал, разумно ожидать, что графен будет демонстрировать нетипичное поведение трения для системы графен-подложка. К сожалению, подробное исследование трения скольжения графена по золотой подложке все еще отсутствует, хотя межфазные свойства между графеном и металлами систематически исследовались [25,26,27,28].

Чтобы заполнить этот пробел, в данной статье поведение трения подвижных графеновых чешуек по единой кристаллической золотой подложке тщательно изучается с помощью моделирования молекулярной динамики (МД). Мы исследуем влияние размера чешуек, формы чешуек, угла относительного вращения между чешуей и подложкой и ориентации кристаллов подложки, чтобы уточнить свойства трения.

Методы

Метод моделирования

Чтобы смоделировать эксперимент АСМ, в котором чешуйка графена, прикрепленная через пружину к наконечнику, скользит по золотой подложке [29], мы создали модель МД, состоящую из чешуи графена, сделанной из N атомы и единственная кристаллическая золотая подложка, см. рис. 1. Три слоя атомов внизу подложки фиксируются в пространстве и служат граничными атомами. Для контроля температуры системы в качестве атомов термостата выбраны четыре слоя атомов, примыкающих к граничным атомам в подложке. Атомы термостата поддерживаются при постоянной температуре 300 K методом масштабирования скорости [30]. В этой статье мы, во-первых, не рассматриваем вращение графена при скольжении; атомам в графене разрешено двигаться только на x и z направления, но ограничены в y направление, что упрощает моделирование. Это основная тема данной статьи. Затем мы дополнительно выполняем некоторые модели МД без ограничения движения графена в y направление, чтобы лучше соответствовать реальным условиям эксперимента. Атомы чешуек увлекаются виртуальным атомом с постоянной скоростью через гармоническую пружину. Пружина, параллельная поверхности подложки, имеет поперечную жесткость 10 Н / м и используется для представления деформации балки кантилевера и вершины наконечника АСМ-системы [31]. Постоянная нормальная нагрузка прикладывается непосредственно к чешуйчатым атомам при моделировании [29, 31]. Чешуйку графена тянет в стороны виртуальный атом с постоянной скоростью 10 м / с. Уравнения движения интегрированы с помощью алгоритма скорости-Верле. Временной шаг составляет 1 фс. Границы периодические по x и y направления, свободный в z направление.

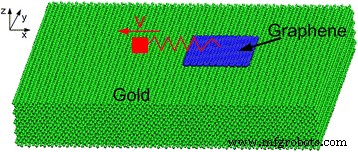
Имитационная модель процесса трения

Чтобы исследовать влияние кристаллической ориентации подложки, мы провели МД-моделирование трения скольжения на трех различных поверхностях плоскостей Au (111), (001) и (110) соответственно. Для поверхности Au (111) системы координат приняты как \ (x- \ left [11 \ overline {2} \ right] \), \ (y- \ left [1 \ overline {1} 0 \ right] \ ) _, и z - [111] и размер 19,98 × 15,0 × 3,06 нм ³ . Для поверхности Au (001) системы координат приняты как x - [100], y - [010] и z- [001] и размер подложки 19,99 × 15,1 × 3,06 нм ³ . Для поверхности Au (110) системы координат приняты как x - [001], \ (y- \ left [1 \ overline {1} 0 \ right] \) _, и z - [110] и размер 19,99 × 15,0 × 3,03 нм ³ . Шаг решетки вдоль направления скольжения для поверхностей Au (111), Au (110) и Au (001) составляет 9,99 Å, 4,08 Å и 4,08 Å соответственно. Если не указано иное, в качестве подложки используется Au (111). При моделировании моделируются несколько различных размеров и форм чешуек. Форма чешуек по умолчанию - квадрат размером 5,8 нм (количество атомов N =1344). x -ось проходит по направлению кресла графена и y - ось идет по зигзагообразному направлению, с z -ось перпендикулярна графену.

Межатомные силы в Au выводятся из потенциала метода погруженного атома (EAM) [32]. Потенциал ЕАМ оказался очень успешным при моделировании упругих свойств, энергии образования дефектов и механизмов разрушения различных металлов [32, 33]. Он также успешно применялся для описания свойств поверхности металлов, таких как поверхностная энергия и реконструкция поверхности [32,33,34]. Широко используемый потенциал AIREBO применяется для описания взаимодействия атомов внутри графена [35]. Взаимодействие между графеном и Au-подложкой моделируется стандартным потенциалом Леннарда-Джонса (LJ), который использовался для изучения многих неравновесных явлений, таких как трение и диффузия кластеров золота на графите [36, 37]. Параметры LJ [28, 29]: ε =22,0 мэВ и σ =2,74 Å. МД моделирования проводятся с использованием крупномасштабного атомно-молекулярного симулятора массового параллелизма (LAMMPS) [38]. При моделировании чешуйка графена изначально располагается над поверхностью подложки из золота. После полного расслабления системы трения виртуальный атом начинает скользить по отрицательному x направление с постоянной скоростью.

Результаты и обсуждения

На рис. 2 показана зависимость силы трения от расстояния скольжения при различных нормальных нагрузках. В этой статье скользящее расстояние - это расстояние виртуального атома. Сила трения измеряется деформацией пружины, как в эксперименте AFM. Чешуйка графена имеет квадратную форму размером 5,8 нм и состоит из 1344 атомов. Понятно, что силы трения непрерывно нарастают с последующими резкими перепадами, что характерно для скачкообразного движения. Резкие спады силы трения приводят к диссипации энергии и предполагают возникновение переходов между множественными метастабильными состояниями с локальными минимумами потенциальной энергии [39]. Разумно, что сила трения увеличивается с увеличением нагрузки L. Для изучения размерного эффекта используются еще две квадратные чешуйки размером 2,0 нм ( N =160 атомов) и 10,0 нм ( N =3936 атомов). Изменение силы трения и средней силы трения для чешуек разного размера во время процесса скольжения показано на рис. 3. Что касается чешуйки толщиной 5,8 нм, очевидное трение прерывистого скольжения также может наблюдаться как для 2,0-, так и для 10- нм хлопья. Более того, явно существует размерный эффект в средней силе трения на атом F _фрик / N, см. Рис. 3c. При той же нагрузке средние силы трения на атом F _фрик / N больше для меньшего хлопья. Этот размерный эффект является результатом прогрессивно уменьшающейся роли кромок в трении с увеличением размера чешуек [40, 41]. Следует отметить, что как эксперименты QCM, так и моделирование методом МД показали, что трение кластеров адсорбата уменьшается с увеличением их размера [18,19,20,21,22], что согласуется с нашими расчетами. Однако размерная зависимость трения в экспериментах QCM и МД-моделировании объясняется зависимой от размера межфазной соизмеримостью [18,19,20,21,22].

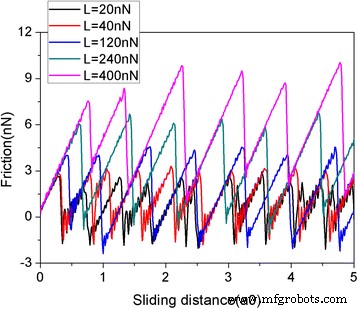
Сила трения как функция расстояния скольжения при различных нормальных нагрузках (L). Чешуйка имеет квадратную форму размером 5,8 нм. Здесь a0 (=9,99 Å) - шаг решетки Au (111) вдоль направления скольжения

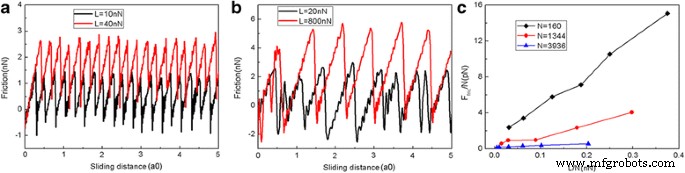
Изменение силы трения и средней силы трения для чешуек разного размера. Типичная сила трения как функция расстояния скольжения для 2,0 нм ( Н =160 атомов) хлопья ( a ) и 10 нм ( N =3936 атомов) хлопь ( b ). c Средняя сила трения на атом ( F _фрик / N) как функция нагрузки на атом (L / N). Здесь a0 (=9,99 Å) - шаг решетки Au (111) вдоль направления скольжения

Поскольку форма ползуна играет важную роль в определении трения [42, 43], для дальнейшего изучения влияния формы чешуек на процесс трения мы также моделируем процесс трения скольжения, используя круглую чешуйку графена ( N =1080 атомов) и треугольной чешуйки графена ( N =654 атома). На рис. 4 показано изменение типичных сил трения и средних сил трения для различных форм чешуек в процессе скольжения. Как показано на рис. 4a, b, при малых нагрузках ( L =20 нН для круглых хлопьев и L =10 нН для треугольной чешуйки) сила трения непрерывно колеблется около нуля, и может наблюдаться сверхнизкое трение (сверхсмазка). Однако при больших нормальных нагрузках ( L =400 нН для круглых хлопьев и L =200 нН для треугольной чешуйки), чешуйка демонстрирует явное скачкообразное движение и большую силу трения [39]. При той же нагрузке средние силы трения на атом F _фрик / N - самые большие для квадратной чешуйки и самые маленькие для треугольной чешуйки, тогда как F _фрик / N для круглых чешуек находятся между ними. Кроме того, разница средних сил трения на атом F _фрик / N между круглой и треугольной чешуей довольно мала. Но F _фрик / N для квадратного отщепа намного больше. Таким образом, очевидно, что форма чешуек играет жизненно важную роль в процессе скольжения.

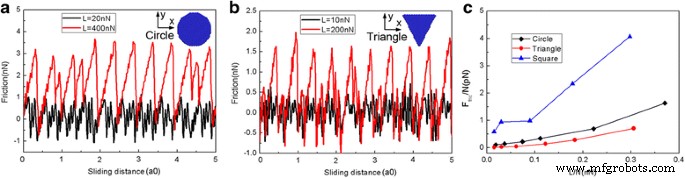
Изменение силы трения и средней силы трения для различных форм чешуек. Типичная сила трения как функция расстояния скольжения для патрона ( Н =1080 атомов) хлопь ( a ) и треугольной ( N =654 атома) хлопь ( b ). c Средняя сила трения на атом ( F _фрик / N) как функция нагрузки на атом (L / N). Здесь a0 (=9,99 Å) - шаг решетки Au (111) вдоль направления скольжения

Хорошо известно, что ориентация чешуйки относительно подложки также имеет решающее значение при определении трения [42]. Чтобы исследовать влияние ориентации на трение, чешуйку графена поворачивают против часовой стрелки на разные углы относительно z -ось перпендикулярна контакту. Угол поворота 0 ° (без поворота) соответствует ситуации, когда x -ось вдоль направления кресла графена, в то время как угол поворота 90 ° соответствует ситуации, когда x - ось по зигзагообразному направлению. Изменение силы трения в зависимости от расстояния скольжения для квадратной чешуйки 5,8 нм с разными углами поворота при L =240 нН показано на рис. 5. Соответствующие средние силы трения F _фрик для разных углов поворота при различных нормальных нагрузках рассчитываются, как показано на рис. 6. Очевидно, что для чешуек с θ =15 ° и θ =45 ° силы трения непрерывно колеблются около нуля, и можно наблюдать сверхсмазку, см. рис. 5б, д. Кроме того, можно наблюдать небольшую разницу в средних силах трения для чешуек с θ =15 ° и θ =45 °, см. Рис. 6. Однако для чешуек с θ =30 °, 60 ° и θ =90 ° хлопья демонстрируют очевидное скачкообразное движение и относительно большую силу трения. Кроме того, средняя сила трения больше для большего угла поворота хлопьев с θ =30 °, 60 ° и θ =90 °. Силы трения для хлопьев с вращением все намного меньше, чем для чешуек без вращения (θ =0 °).

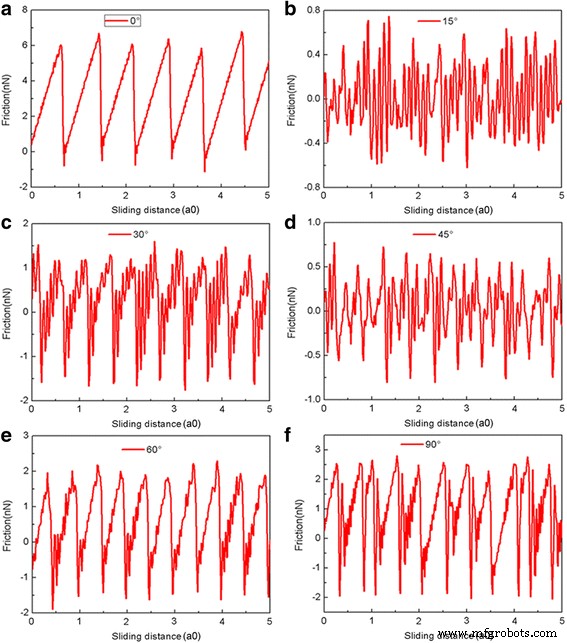
Зависимость силы трения от расстояния скольжения квадратной чешуйки 5,8 нм при L =240 нН для разных углов поворота (θ =0 °, 15 °, 30 °, 45 °, 60 °, 90 °). а - е соответствуют углу поворота 0 ° ~ 90 ° соответственно. Здесь a0 (=9,99 Å) - шаг решетки Au (111) вдоль направления скольжения

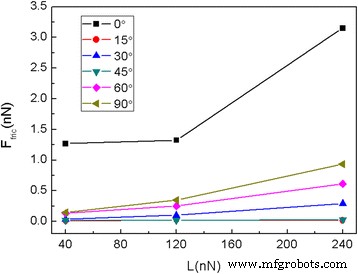
Средняя сила трения Ffric квадратной чешуйки 5,8 нм для разных углов поворота при разных нормальных нагрузках

Тот факт, что монокристаллическое золото проявляет значительные анизотропные эффекты, побуждает нас продолжить изучение влияния ориентации кристаллов подложки на процесс трения. Мы провели моделирование МД еще для двух комбинаций ориентации кристалла и направления скольжения, то есть (001) [100] и (110) [001]. Сила трения и средняя сила трения F _фрик Скольжение квадратной чешуйки 5,8 нм по подложкам из золота с различной ориентацией кристаллов показано на рис. 7 и 8 соответственно. Как и ожидалось, сила трения увеличивается с нормальной нагрузкой. Видно, что при одинаковой нагрузке силы трения для поверхностей Au (001) и Au (110) больше, чем для поверхности Au (111), а силы трения для поверхности Au (110) равны самый большой.

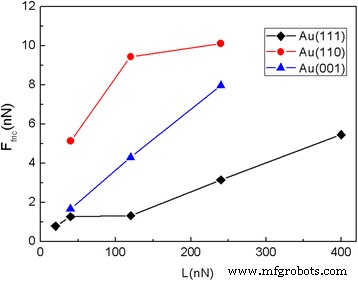
Сила трения квадратной чешуйки 5,8 нм, скользящей по ( a ) Au (001) и ( b ) Поверхности Au (110) как функция расстояния скольжения при различных нормальных нагрузках. Здесь a1 (=4,08 Å) - это шаг решетки Au (001) вдоль направления скольжения, а a2 (=4,08 Å) - шаг решетки Au (110) вдоль направления скольжения

Средняя сила трения F _фрик квадратной чешуйки размером 5,8 нм, скользящей по подложкам из золота с различной ориентацией кристаллов при различных нормальных нагрузках

Согласно хорошо известной модели Прандтля-Томлинсона [44], сила трения тесно связана с гофрировкой межфазной энергии [45,46,47]. Чтобы изучить основные механизмы, лежащие в основе значительного анизотропного эффекта трения, мы рассчитали потенциальную энергию взаимодействия между чешуей и подложкой из золота при изменении положения чешуек [46]. Потенциальная энергия рассчитывается для твердой пластины на фиксированной высоте, которая соответствует средней высоте для данной нагрузки [29]. Три типичных контурных графика, представляющих пространственное изменение потенциальной энергии для поверхностей Au (111), Au (110) и Au (001) на L =120 нН показаны на рис. 9а – в соответственно. Чтобы получить карты поверхности потенциальной энергии (ППЭ) на рис. 9, мы используем 21 точку сетки вдоль обеих точек x и y направления. На рис. 9 гофры энергии, рассчитанные для Au (111), Au (110) и Au (001), составляют 3,5 эВ, 66,6 эВ и 29,1 эВ соответственно. На рис. 9a – c сплошная черная линия ( y =0) на картах PES используется для отображения траектории скольжения отщепа. Потенциальная энергия взаимодействия графена и золота вдоль дорожки скольжения для Au (111), Au (110) и Au (001) также представлена ​​на рис. 9d – f соответственно. Энергетические гофры вдоль дорожки скольжения для Au (111), Au (110) и Au (001) на рис. 9 составляют 3,5 эВ, 59,7 эВ и 29,1 эВ соответственно. Хорошо видно, что амплитуда гофрировки энергии проявляет такой же анизотропный эффект, что и трение. Энергетическая гофра для поверхностей Au (001) и Au (110) больше, чем для поверхности Au (111), а энергетическая гофра для поверхности Au (110) является наибольшей. Следовательно, это ясно объясняет значительный анизотропный эффект трения во время процесса скольжения [45,46,47]. Вывод о том, что сила трения уменьшается с уменьшением силы взаимодействия графен-подложка (энергетическая гофра), согласуется с расчетами МД [16] и экспериментом QCM [17].

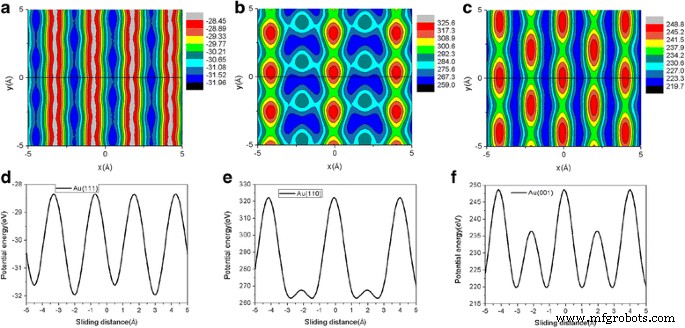
Контурные карты потенциальной энергии для поверхности Au (111), Au (110) и Au (001) на L =120 нН показаны в a - c , соответственно. Используется квадратная чешуйка графена 5,8 нм. В а - c , черная сплошная линия ( y =0) на картах используется, чтобы показать траекторию скольжения отщепа. Потенциальная энергия взаимодействия графена и золота вдоль пути скольжения для поверхностей Au (111), Au (110) и Au (001) также представлена ​​на d . - е , соответственно. Единица потенциальной энергии - эВ. Средняя высота отщепа на L =120 нН для поверхности Au (111), Au (110) и Au (001) составляет 2,36 Å, 2,1 Å и 2,17 Å соответственно

Чтобы лучше соответствовать реальным условиям эксперимента, мы дополнительно выполнили МД-моделирование трения скольжения без ограничения движения графена в y направлении, и в этом случае чешуйка может вращаться и двигаться по y направление. На рисунке 10 показана зависимость силы трения от расстояния скольжения при различных нормальных нагрузках для чешуйки графена квадратной формы и размером 5,8 нм, состоящей из 1344 атомов. Хотя значения силы трения изменились, можно увидеть, что силы трения постоянно увеличиваются, а затем резко падают, что является очевидным скачкообразным движением, аналогичным показанному на рис. 2. Сила трения увеличивается с нагрузкой, как и ожидалось. Мы также изучили процесс трения еще двух квадратных чешуек графена размером 2,0 нм ( N =160 атомов) и 10,0 нм ( N =3936 атомов) без ограничения движения графена в y направление. Изменение силы трения и средней силы трения для чешуек разного размера во время процесса скольжения показано на рис. 11. Как и на рис. 3, мы также наблюдаем явное трение прерывистого скольжения для чешуек размером 2,0 и 10 нм. Кроме того, существует размерный эффект средней силы трения на атом F _фрик / N, см. Рис. 11c. При одинаковых нагрузках средние силы трения на атом F _фрик / N больше для более мелкой чешуйки, что типично для размерного эффекта трения. В целом, мы обнаружили, что основные результаты МД-моделирования процесса трения с y -направленное движение чешуйки с ограничениями по-прежнему сохраняется после ослабления ограничения движения графеновой чешуйки в y направление при скольжении.

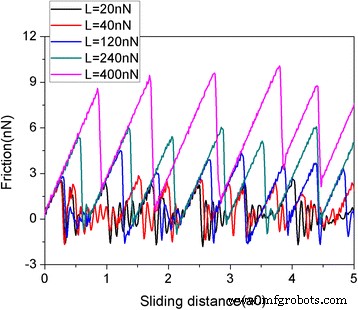
Сила трения как функция расстояния скольжения при различных нормальных нагрузках ( L ) для процесса трения без ограничения движения графена в y направление. Чешуйка имеет квадратную форму размером 5,8 нм. Здесь a0 (=9,99 Å) - шаг решетки Au (111) вдоль направления скольжения

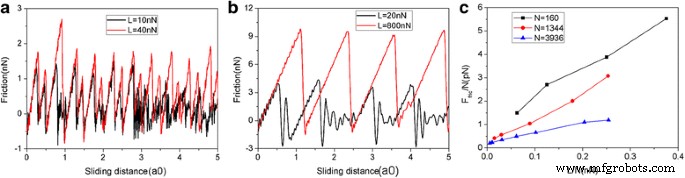
Изменение силы трения и средней силы трения для различных размеров чешуек для процесса трения без ограничения движения графена в y направление. Типичная сила трения как функция расстояния скольжения для 2,0 нм ( Н =160 атомов) хлопья ( a ) и 10 нм ( N =3936 атомов) хлопь ( b ). c Средняя сила трения на атом ( F _фрик / N) как функция нагрузки на атом (L / N). Здесь a0 (=9,99 Å) - шаг решетки Au (111) вдоль направления скольжения

Выводы

В этой работе моделирование молекулярной динамики используется для исследования поведения трения скольжения мобильных графеновых чешуек по единой кристаллической золотой подложке. Влияние размера чешуек, формы чешуек, угла относительного вращения и ориентации кристаллов подложки тщательно изучено. Обнаружено, что существует размерный эффект в поведении трения. При той же нагрузке средние силы трения на атом F _фрик / N больше для меньшего размера чешуйки графена. Также обнаружено, что форма чешуек играет важную роль в процессе трения. Средние силы трения на атом F _фрик / N для квадратных чешуек намного больше, чем для треугольных и круглых чешуек. Кроме того, средние силы трения на атом F _фрик / N для отщепа треугольной формы самые маленькие. Мы также обнаружили, что влияние ориентации чешуйки графена относительно Au-подложки является критическим при определении трения. Силы трения для чешуйки графена, скользящей в направлении кресла, намного больше, чем для хлопьев с вращением. Сверхмалые силы трения наблюдаются для чешуек с θ =15 ° и θ =45 °. Кроме того, сила трения больше для большего угла поворота хлопьев с θ =30 °, 60 ° и θ =90 °. Кроме того, обнаружено, что трение проявляет значительный анизотропный эффект. Силы трения для поверхностей Au (001) и Au (110) больше, чем для поверхности Au (111), а силы трения для поверхности Au (110) самые большие. Этот анизотропный эффект трения объясняется анизотропным эффектом гофрирования потенциальной энергии. Эти результаты не только дают представление о механизмах, лежащих в основе скольжения графеновых чешуек по золотой подложке, но также могут служить ориентиром при проектировании и производстве наноразмерных устройств на основе графена.