Моделирование молекулярной динамики механизма резания в процессе гибридной обработки монокристаллического кремния

Введение

Монокристаллический кремний является важным полупроводниковым материалом, который широко используется в инфракрасной оптике, микроэлектронике и оптоэлектронных системах благодаря своим превосходным оптическим и механическим свойствам [1, 2]. Однако из-за твердости и хрупкости монокристаллического кремния во время механической обработки могут возникать микроскопические хрупкие трещины и подповерхностные повреждения. Во время процесса микрофрезерования в заготовке могут возникать дефекты скалывания кромок внутреннего типа, вызванные механической обработкой [3]. При обработке монокристаллической алмазной резкой (SPDT) в зависимости от параметров обработки может образовываться поврежденный слой от 200 до 600 нм [4, 5]. Хотя подповерхностный поврежденный слой можно уменьшить примерно до 50 нм путем шлифовки и полировки. Эффективность обработки и возможности изготовления сложных конструкций ограничены. Чтобы преодолеть эти проблемы, были предложены и испытаны различные вспомогательные технологии обработки. В частности, термическая резка (TAC) [6] и резка с использованием вибрации (VAC) [7] привлекли широкое внимание как ее исключительные режущие характеристики.

Для хрупких материалов, таких как монокристаллический кремний, переход от хрупкого к пластичному может усиливаться при повышении температуры обработки. Во время процесса ТАС кремниевая заготовка термически размягчается, что вызывает уменьшение сил резания [8] и удельной энергии резания [9, 10]. Между тем, отжиг фаз высокого давления в кубическую фазу кремния становится очевидным при повышении температуры обработки [11]. При соответствующем выборе параметров обработки желаемая обработанная поверхность с высокой фазовой чистотой и низким внутренним повреждением может быть достигнута с помощью TAC [12,13,14]. В дополнение к TAC, резка с помощью вибрации (VAC) - еще один метод, способствующий достижению высококачественной поверхности на монокристаллическом кремнии. Этот метод применяется в обрабатывающей промышленности с 1960-х годов [15]. На начальном этапе развития этой технологии при обработке применялось только линейное вибрационное движение в номинальном направлении резания, которое называется линейной вибрационной резкой (LVC). В 1994 году Шамото и Мориваки [16] предложили эллиптическую вибрационную резку (EVC). Таким образом, возможность обработки EVC на многих хрупких материалах, таких как кремний [17, 18], реакционно-связанный карбид кремния [7], карбид вольфрама [19, 20] и закаленная сталь [21], была подтверждена. Во время процесса EVC подповерхностное повреждение может быть эффективно подавлено, поскольку переходная глубина резания (DOC) намного меньше номинальной DOC [22]. Кроме того, из-за разделения в каждом цикле вибрации контактные поверхности между режущим инструментом и заготовкой подвергаются воздействию окружающего газа или жидкости, которые рассеивают выделяемое при резании тепло. Таким образом, износ режущего инструмента, такой как адгезия и термохимическая реакция [23], может быть эффективно подавлен.

Для дальнейшего улучшения обрабатываемости хрупких материалов были проведены эксперименты по гибридной механической обработке (HM), сочетающие тепловой и вибрационный ассистенты [24, 25]. Было обнаружено, что при резке Inconel 718 методом HM можно эффективно уменьшить шероховатость обработанной поверхности [26]. С помощью экспериментов и моделирования методом конечных элементов (МКЭ) можно добиться существенного снижения сил резания и превосходного качества поверхности титановых сплавов во время процесса ТМ [27]. Эти результаты демонстрируют возможность применения метода HM для прецизионной обработки хрупких материалов. Однако трудно непосредственно наблюдать и измерять физические переменные во время процесса обработки, поскольку режущий инструмент вибрирует с высокой частотой, а зона деформации находится при высокой температуре. Кроме того, при изготовлении нанометрической поверхности толщина удаления переходного материала обычно составляет от субнанометров до нескольких нанометров. Поэтому традиционное континуальное представление проблемы, такое как МКЭ, вызывает сомнения, поскольку квантово-механические эффекты становятся очевидными.

В последние годы моделирование молекулярной динамики (МД) широко применяется в исследованиях процесса вспомогательной обработки из-за его преимуществ при изучении процесса нанометрической резки [28,29,30]. Основываясь на предыдущем моделировании TAC [31], когда температура резания увеличивается, анизотропия силы резания, удельной энергии резания и напряжения текучести становится более очевидной. Между тем, сила сдвига в заготовке ниже при более высокой температуре резания, что приводит к более узким зонам сдвига и большим значениям угла плоскости сдвига [32]. Кроме того, скорость съема материала может быть улучшена с увеличением температуры резания, поскольку образуется больше стружки [33]. Для процесса EVC с помощью МД-моделирования было обнаружено, что сжимающее напряжение и напряжение сдвига в области деформации могут быть значительно уменьшены по сравнению с обычным резанием [34], что является преимуществом для подавления подповерхностных повреждений. Кроме того, процесс EVC показывает очевидное уменьшение толщины стружки, что приводит к увеличению отношения толщины неразрезанной стружки к толщине стружки [35]. Кроме того, было обнаружено, что параметры вибрации, включая отношения амплитуд, частоты колебаний и разность фаз, имеют большое влияние на эффективность удаления материала [34, 36].

Эти замечательные достижения улучшили понимание механизма обработки для вспомогательного процесса обработки. Однако для экономии времени вычислений и памяти системы моделирования обычно довольно малы. В предыдущих моделях процесса EVC амплитуды вибрации и номинальный DOC были менее 5 нм [22, 36]. Следовательно, толщина удаления переходного материала обычно составляет менее 1 нм, что не позволяет точно описать фактический процесс удаления материала. Кроме того, не сообщалось о моделировании процесса ГМ методом МД. Механизм процесса удаления материала и образования подповерхностных повреждений во время процесса ТМ до сих пор не ясен. Поэтому в данной статье МД моделирование проводится для выявления режущего механизма процесса ТМ. Классическая модель резания модифицирована так, что параметры вибрации намного ближе к экспериментальным значениям, например, амплитуда вибрации увеличена до 40 нм при номинальной скорости резания 3,125 м / с. Исследован механизм снятия материала за один цикл вибрации и влияние повышенной температуры резания. МД-моделирование проводится с помощью известного крупномасштабного атомно-молекулярного массивно-параллельного симулятора (LAMMPS) [37]. Программа постобработки OVITO [38] используется для анализа результатов моделирования.

Метод моделирования

Подробная информация о модели резки

На рисунке 1 показана схематическая диаграмма процесса EVC, которая первоначально была представлена ​​Shamoto et al. [39]. Траекторию инструмента можно выразить как:

где x ( т ) и z ( т ) представляют смещение режущего инструмента в x и z направления. А _c и A _d - амплитуда вибрации в номинальном направлении резания ( x направление) и номинальное направление DOC (отрицательное z направление). Параметры f , v , φ , и t представляют частоту вибрации, номинальную скорость резания, разность фаз и время моделирования соответственно. Время моделирования t _я представляет время точки P _я по траектории инструмента с рис. 1.

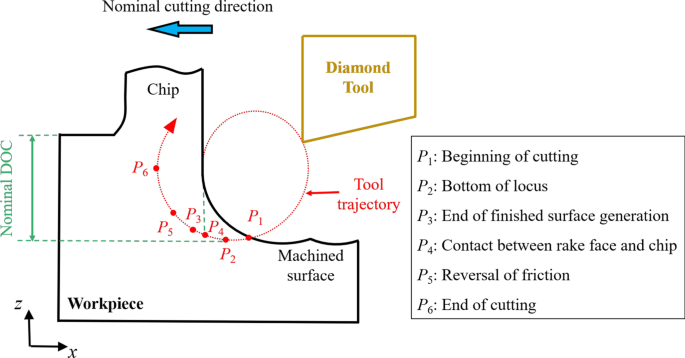
Принципиальная схема процесса EVC

Согласно геометрическому соотношению [40], значение t ₁ и t ₃ можно определить по:

Затем t ₆ может быть получено, когда переходное направление движения алмазного инструмента параллельно передней грани инструмента:

где γ - передний угол алмазного режущего инструмента.

Модель МД представлена ​​на рис. 2. Заготовка из монокристаллического кремния выполнена в виде деформируемого тела. Алмазный инструмент считается твердым телом, поскольку в этом моделировании износом инструмента можно пренебречь. Морфология заготовки в классической модели резания изменена в соответствии с траекторией инструмента в предыдущем цикле вибрации с учетом радиуса кромки инструмента. Траекторию инструмента можно определить, как показано на рис. 2b. P _о и P _b являются центром и нижней точкой окружности кромки инструмента. Когда учитывается эффект кромки инструмента, точка образования переходной поверхности P _c изменяется вдоль кромки инструмента во время движения инструмента. Фактическая обработанная поверхность формируется линией огибающей кромки режущего инструмента. Если траектория P _b выражается уравнениями. (1) и (2) траектория P _c можно вычислить с помощью [41]:

где

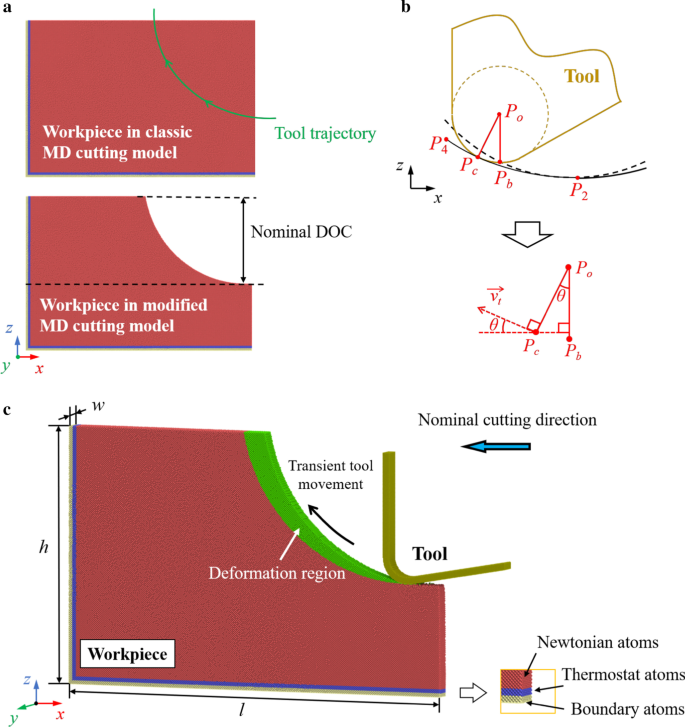
Схема режущей модели МД. а Доработка заготовки. б Определение траектории инструмента. c Морфология модифицированной МД-модели. Зеленые атомы представляют собой область деформации за один цикл колебаний

Атомы кремния делятся на три группы:граничные атомы, атомы термостата и ньютоновские атомы. Граничные атомы фиксируются в своих уравновешенных положениях, чтобы удерживать заготовку во время моделирования. Атомы термостата поддерживаются при температуре окружающей среды, чтобы рассеять выделяемое при резке тепло, в то время как атомы Ньютона подчиняются второму закону Ньютона.

Подробная информация о параметрах моделирования приведена в Таблице 1. Длина l и высота h были определены, чтобы сохранять достаточное расстояние между зоной резания и фиксированными границами. Периодическое граничное условие применяется вдоль y направление имитировать объемный кремний. Номинальное направление резания, передний угол инструмента / задний угол и разность фаз определялись на экспериментальной установке [42]. Амплитуда вибрации и номинальный DOC увеличены, чтобы приблизиться к экспериментальному масштабу с приемлемой стоимостью моделирования. Между тем, чтобы гарантировать толщину удаляемого материала (зеленые атомы на рис. 2c), соотношение скоростей и частота колебаний были установлены на 40 и 500 МГц соответственно. Поэтому номинальная скорость резания была определена как 3,125 м / с. Кроме того, проводится моделирование с различной температурой резки, чтобы выявить влияние теплового ассистента на механизм резки. Температура резания повышается с 300 до 1200 К, что реализуемо во время TAC, например, лазерной обработки [4, 11].

В этой модифицированной модели моделируется только этап резания во время цикла вибрации, и сохраняются временные интервалы, когда заготовка отделяется с помощью режущего инструмента. Следовательно, вычислительная мощность может быть сосредоточена на переходном процессе резания. Самое главное, можно точно описать процесс удаления переходного материала. Сравнение модифицированной модели и классической модели MD показано в таблице 2.

Возможная функция

При моделировании МД важно использовать надежный потенциал для описания взаимодействия между атомами. Для монокристаллического кремния ученые разработали множество возможностей, таких как модифицированный метод встроенного атома (MEAM) [45], метод Стиллингера – Вебера (SW) [46], Tersoff [47] и многочастичный метод с оптимизацией заряда (COMB) [ 48] потенциалов. Среди этих потенциалов все большее внимание привлекает аналитический потенциал порядка связи (ABOP), предложенный Эрхартом и Альбе [49]. Это трехчастичная потенциальная функция, которая позволяет образовывать и разрывать связи во время моделирования обработки. Согласно предыдущим исследованиям [50], ABOP может точно описывать как димерные, так и объемные свойства кремния. Между тем, механические свойства кремния, полученного с помощью ABOP, хорошо согласуются с экспериментами [31], что важно при моделировании МД наноразмерной обработки. Поэтому в этой статье потенциал ABOP применяется для описания взаимодействий кремний – кремний и углерод – углерод. Между тем, взаимодействие кремний-углерод описывается потенциалом Морзе, который был доказан как эффективный потенциал при моделировании резки на наноуровне [51, 52]. Потенциальная функция Морзе может быть выражена как:

где D _M , а, и R _M представляет собой энергию сцепления, модуль упругости и равновесное расстояние между атомами соответственно. Параметры потенциала Морзе [53]: D _M =0,435 эВ, a =46,487 нм ⁻¹ , R _M =0,19475 нм.

Результаты и обсуждение

Высокая эффективность

При обычной резке на основной механизм удаления материала может сильно влиять недеформированная толщина стружки [54]. При небольшой толщине недеформированной стружки основным механизмом удаления материала является экструзия. Металлическая стабильная фаза (Si-II) может быть получена за счет фазового перехода под высоким давлением (HPPT), который способствует пластической деформации кремния. Когда толщина недеформированной стружки увеличивается, материал может быть удален в основном путем резки. В процессе EVC, поскольку толщина недеформированной стружки постоянно меняется, механизм удаления материала может трансформироваться от экструзии к резке за один цикл вибрации. На рисунке 3 показаны снимки моделирования резания при 300 К. Кристаллическая структура заготовки определяется анализом общих соседей (CNA) [55]. Этот анализ обнаруживает атомы, которые расположены в кубической или гексагональной решетке алмаза. Неалмазная структура на рис. 3c, e в основном содержит аморфную фазу (a-Si), Si-II и другие дефектные атомы [56]. Эти структуры нестабильны и после резки превращаются в a-Si. Из рис. 3b, c видно, что на начальной стадии резки материал в основном удаляется путем экструзии. Возле кромки режущего инструмента может наблюдаться переходная точка застоя. Как и при обычном резании, материалы в области деформации разделяются по точке застоя на стружку и сжатый материал. По мере движения режущего инструмента толщина недеформированной стружки увеличивается. В заготовке образуются плоскости сдвига и поликристаллические зерна, что указывает на то, что сдвиг становится доминирующим механизмом удаления материала.

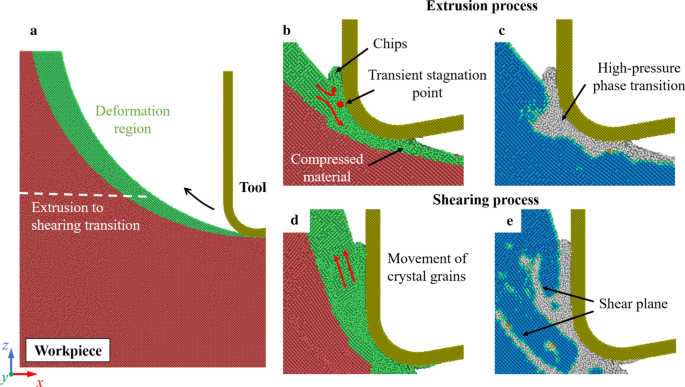
Переход механизма удаления материала. а Иллюстрация области деформации. б , d Процесс экструзии и резки. c , e Идентификация кристаллической структуры детали. Синие атомы представляют кубическую структуру алмаза, а серые атомы - неалмазную структуру

На рис. 4 показана морфология заготовки при различных температурах резания. При 300 К в заготовке во время движения инструмента вверх наблюдаются явные трещины и излом. Для хрупкого материала, такого как монокристаллический кремний, движение инструмента вверх привело бы к отрыву материала и оставлению дефектов в заготовке, что рассматривается как особая проблема в EVC [42]. Хотя эти трещины можно удалить с помощью дополнительных циклов вибрации, стабильность обработки будет снижена из-за неровности поверхности заготовки. Когда температура резания повышается, образование и распространение трещин эффективно подавляется. Из рис. 4d видно, что при повышении температуры резания до 1200 К не обнаруживается явного разрушения. Однако наблюдается, что при 900 К и 1200 К набухание обработанной поверхности становится очевидным, когда механизм удаления материала трансформируется в резку. Можно сделать вывод, что по мере того, как на стадии сдвига образуется больше кристаллических зерен, набухание может быть вызвано вращением этих кристаллических зерен при высокой температуре.

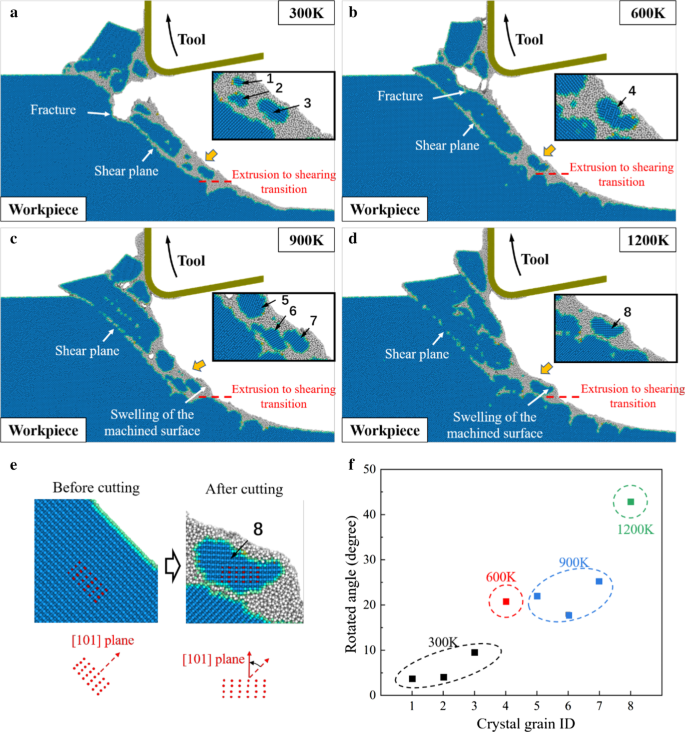
Морфология детали процесса HM на a 300 тыс. б 600 тыс. c 900 тыс. д 1200 К. Синие атомы представляют собой кубическую структуру алмаза, а серые атомы - неалмазную структуру. е Определение угла поворота кристаллических зерен. е Угол поворота при повышении температуры резания

Для четкого описания этого вращения координаты 24 отмеченных атомов (красных атомов) в кристаллических зернах используются для расчета среднего угла поворота, как показано на рис. 4e. Угол поворота 8 кристаллических зерен (пронумерованных на рис. 4a – d) суммирован на рис. 4f. Видно, что угол поворота явно увеличивается при повышенной температуре. Во время процесса HM вязкость a-Si может быть значительно снижена при высокой температуре, а движение атомов в заготовке стимулируется движением инструмента вверх. Следовательно, поток атомов в заготовке усиливается, и можно облегчить вращение кристаллических зерен, что приводит к разбуханию обработанной поверхности. Чтобы ограничить вращение кристаллических зерен, мощность нагрева следует контролировать, чтобы избежать перегрева заготовки. Кроме того, следует тщательно выбирать параметры вибрации, например, следует применять меньшую номинальную скорость резания и более высокую частоту вибрации, чтобы подавить образование кристаллических зерен и устранить набухание при последующих циклах вибрации. Как показано на рис. 5, при соответствующих параметрах вибрации P ₁ может располагаться на стадии экструзии, и окончательная обработанная поверхность создается путем экструзии без разбухания.

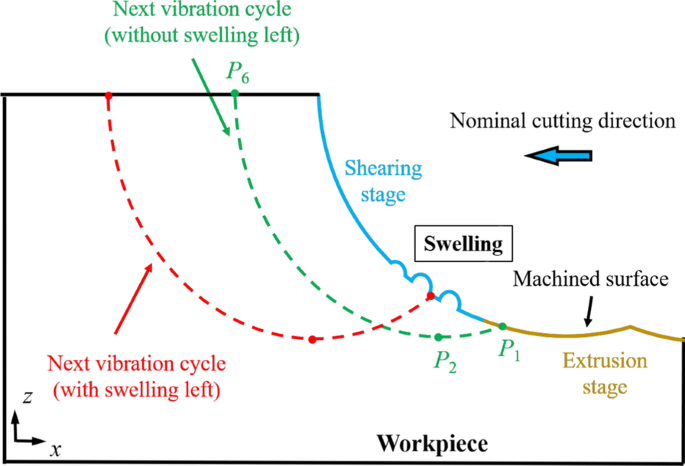
Устранение набухания в процессе ГМ

Поле напряжений в заготовке

Для дальнейшего изучения механизма резания во время процесса HM было рассчитано распределение напряжений в заготовке. В моделировании МД гидростатическое напряжение может быть выражено как:

где σ _x , σ _y , и σ _z , - тензоры напряжений из выходных данных LAMMPS.

Распределение гидростатических напряжений на стадиях экструзии и сдвига показано на рис. 6. Были отмечены пиковые значения напряжений в областях сжатия и растяжения. При перемещении инструмента точка контакта между инструментом и заготовкой изменяется в течение цикла кромки инструмента, что приводит к перемещению области сжатия от кромки инструмента к передней поверхности. Согласно предыдущим сообщениям, HPPT из фазы монокристаллического кремния (Si-I) в Si-II может происходить при давлениях, начиная с 10–12 ГПа [57, 58]. При моделировании резания при 300 K максимальное сжимающее напряжение на стадии экструзии и сдвига достигло 18,1 ГПа и 17,6 ГПа соответственно. Этот результат указывает на то, что пластичная фаза Si-II может образовываться во время резки, а HPPT все еще существует на стадии резки. Кроме того, на стадии экструзии растягивающее напряжение в основном концентрируется вблизи области контакта между боковой поверхностью инструмента и обработанной поверхностью в результате адгезии атомов кремния и поверхности инструмента. Когда инструмент переходит в стадию сдвига, область растяжения увеличивается, и концентрация растягивающих напряжений в подповерхностной заготовке значительно увеличивается, что вызвано подъемным движением. Когда температура резки увеличивается, пластическая деформируемость монокристаллического кремния улучшается, а внутреннее напряжение в заготовке уменьшается. При повышении температуры от 300 до 1200 К максимальное сжимающее напряжение уменьшилось на 16,6% и на 25% на стадии экструзии и сдвига. Между тем, хотя концентрация растягивающего напряжения в подповерхностной заготовке все еще очевидна, пиковое значение растягивающего напряжения очевидно снижается более чем на 30%. Сообщалось, что вязкость разрушения монокристаллического кремния можно эффективно повысить при более высокой температуре [59]. Таким образом, можно эффективно подавить трещины и изломы, вызванные эффектом отрыва из-за движения инструмента вверх.

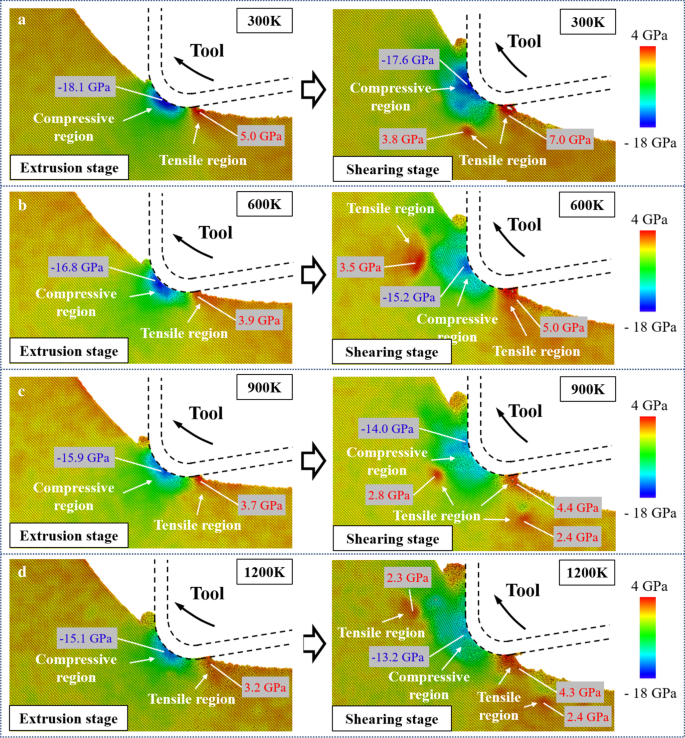
Распределение гидростатического напряжения в: a 300 тыс. б 600 тыс. c 900 тыс. д 1200 тыс.

Монокристаллический кремний имеет кристаллическую структуру Face Center Cubic (FCC) с 12 системами скольжения. Основываясь на движении инструмента, основными системами скольжения для деформации сдвига являются (111) / [\ (\ stackrel {\ mathrm {-}} {1} \) 01] и (1 \ (\ stackrel {\ mathrm {- }} {1} \) 1) / [\ (\ stackrel {\ mathrm {-}} {1} \) 01] систем. Следовательно, разрешенная составляющая напряжения сдвига τ _s в системе скольжения (111) / [\ (\ stackrel {\ mathrm {-}} {1} \) 01] рассчитывается. Как показано на рис. 7, разрешенная составляющая напряжения сдвига τ _s по направлению M плоскости скольжения N можно рассчитать с помощью тензоров напряжений:

где a ₁ , b ₁ , c ₁ - направляющие косинусы нормального направления плоскости N а а ₂ , b ₂ , c ₂ - направляющие косинусы направления скольжения M . Пока τ _xy , τ _xz , и τ _yz - тензоры напряжения сдвига из выходных данных LAMMPS.

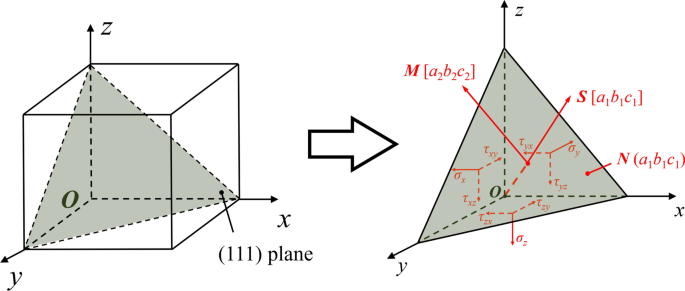
Иллюстрация тензоров напряжений

Распределение разрешенного напряжения сдвига τ _s показан на рис. 8. Область с положительным значением τ _s определяется как область сдвига, поскольку продвигается движение скольжения в направлении [\ (\ stackrel {\ mathrm {-}} {1} \) 01], что облегчает удаление материала за счет сдвига. В то время как область с отрицательным τ _s считается областью повреждения, потому что движение скольжения предпочтительно в противоположном направлении, что приводит к образованию подповерхностных повреждений в заготовке. На стадии экструзии напряжение в области сдвига меньше, чем в области повреждения. Поверхностные повреждения, вызванные деформацией сдвига, могут возникать под обработанной поверхностью [60]. По мере движения режущего инструмента напряжение сдвига в направлении [\ (\ stackrel {\ mathrm {-}} {1} \) 01] постепенно увеличивается, что приводит к переходу удаления материала от экструзии к сдвигу. Кроме того, поскольку положение области повреждения перемещается вверх по ходу движения инструмента, образовавшееся повреждение может быть устранено посредством дальнейшего цикла вибрации и не останется в заготовке. При повышении температуры с 300 K до 1200 K напряжение сдвига в области повреждения уменьшилось на 36,1% и 42,4% на стадии экструзии и сдвига, соответственно. Напротив, из-за движения инструмента вверх, уменьшение напряжения сдвига в направлении [\ (\ stackrel {\ mathrm {-}} {1} \) 01] на стадии сдвига гораздо менее очевидно. Критическое разрешенное напряжение сдвига (CRSS) для движения скольжения может быть выражено как [61]:

где U и ε представляют собой энергию активации скольжения и скорость деформации. Параметры n и C материальные константы. Можно сделать вывод, что CRSS, очевидно, может уменьшаться с повышением температуры. Следовательно, деформация сдвига в направлении [\ ({\ overline {\ text {1}}} \) 01] может быть облегчена при повышенной температуре.

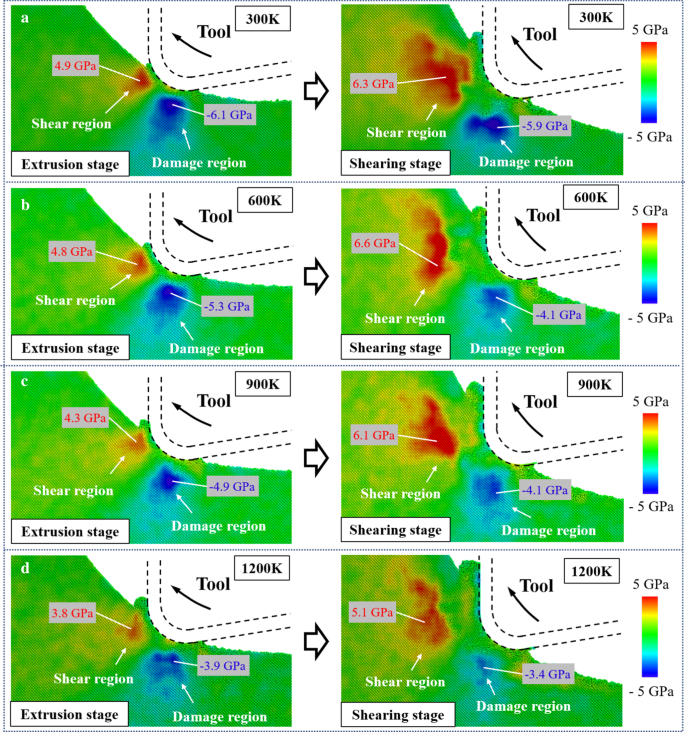
Разрешенное распределение напряжения сдвига в: a 300 тыс. б 600 тыс. c 900 тыс. д 1200 тыс.

Фазовый переход

При повышении температуры резания можно сильно повлиять на фазовый переход кремния. Релаксации a-Si и переходу к Si-I может способствовать соответствующая температура [62]. На рис. 4 картина повреждения деталей сужается при высокой температуре. Подробное наблюдение картины повреждения при резке при 1200 К представлено на рис. 9а. Наблюдается, что образовавшееся повреждение в области деформации частично восстанавливается после резки, указывая на то, что произошел переход от неалмазной структуры к Si-I. При повышении температуры резания образуется больше атомов Si-I, как показано на рис. 9b. Кроме того, построенная поверхностная сетка (красный цвет) [63] обработанной детали при 1200 K представлена ​​на рис. 9c. Наблюдается образование некоторых вакансий в приповерхностной заготовке. Поскольку атомы в фазе Si-I более плотно упакованы, переход к Si-I может вызвать усадку материала, что приводит к появлению вакансий в заготовке. Объем вакансий при разных температурах рассчитан и представлен на рис. 9г. Отмечено, что при комнатной температуре вакансии практически не образуются. В то время как явное увеличение вакансий можно обнаружить при повышении температуры резки до 900 К и 1200 К.

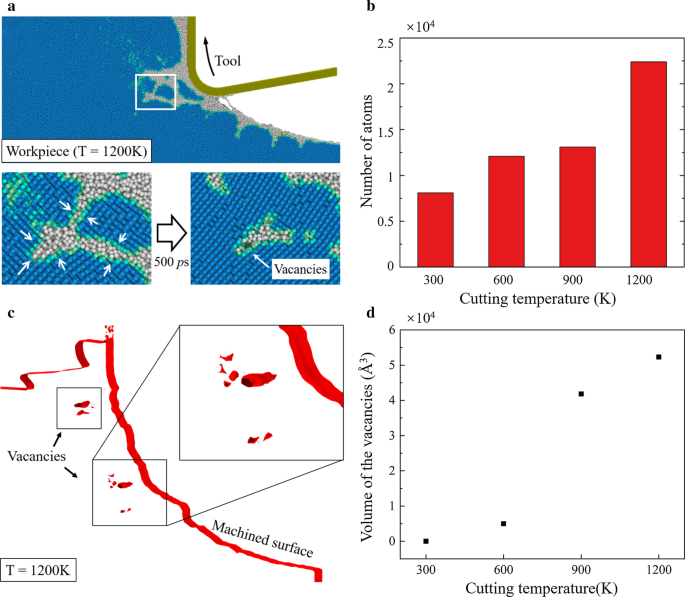
Процесс релаксации и вакансии в заготовке. а Снимок картины повреждений детали при 1200 К. b Число атомов, перешедших из неалмазной структуры в фазу Si-I. c Построенная поверхностная сетка заготовки при 1200 К. d Объем вакансий при разных температурах

Дальнейший анализ вакансий представлен на рис. 10. Материальный элемент под обработанной поверхностью выбирается для контроля образования вакансий. Присутствуют количество атомов в неалмазной структуре и эволюция напряжения материального элемента. Сделан вывод, что во время процесса резания элемент материала сначала сжимается, а затем испытывает растягивающее напряжение из-за движения инструмента вверх. Между тем, два пика напряжения сдвига можно наблюдать при 300 К, поскольку напряжение сдвига в области повреждения увеличивается при прохождении режущего инструмента. При повышении температуры резания уменьшение напряжения сдвига более очевидно, чем напряжение растяжения. При 1200 K второй пик напряжения сдвига практически исчезает, а в элементе материала в процессе релаксации растягивающее напряжение становится доминирующим.

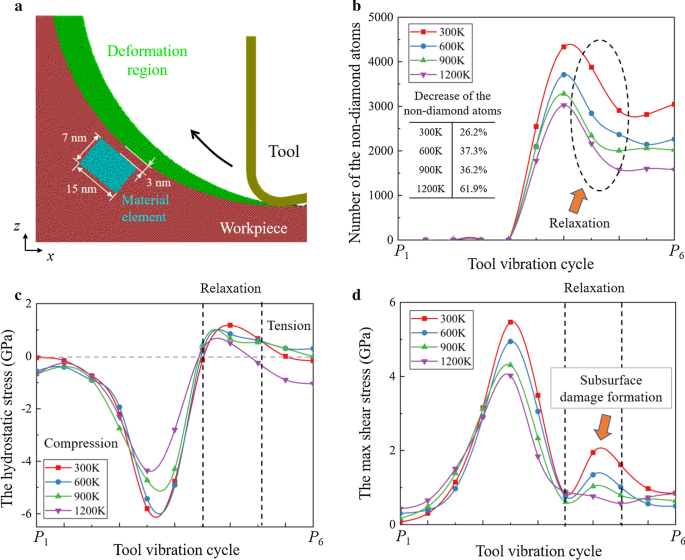
Расслабление во время процесса HM. а Иллюстрация материального элемента. б Статистика атомов в неалмазной структуре в материальном элементе. c , d Эволюция напряжений в материальном элементе

Для изучения влияния растягивающего напряжения на процесс образования вакансий было проведено релаксационное моделирование объемного образца кремния. Как показано на рис. 11а, исходная модель состоит из 40% атомов Si-I и 60% атомов a-Si, которая генерируется методом плавления-закалки [64]. Размер модели 21,7 нм × 8,1 нм × 26,1 нм в x , y , и z направление, которое содержит 230 400 атомов. The initial interface between crystal and non-crystal region is set as (001) crystal plane. Periodic boundary condition is applied in three dimensions to mimic bulk materials. The constructed surface mesh of the relaxed model is present in Fig. 11b. Furthermore, to quantify the vacancies, the solid volume fraction is calculated as the ratio of the solid material volume and the total volume of the simulation sample, as shown in Fig. 11c. It is observed that when temperature is increased, the solid volume fraction decreased obviously under tensile stress. Therefore, to suppress the vacancies, the desired cutting temperature in HM process should be lower than that in ordinary TAC. Meanwhile, the vibration parameters should be optimized to reduce the tensile stress in subsurface workpiece.

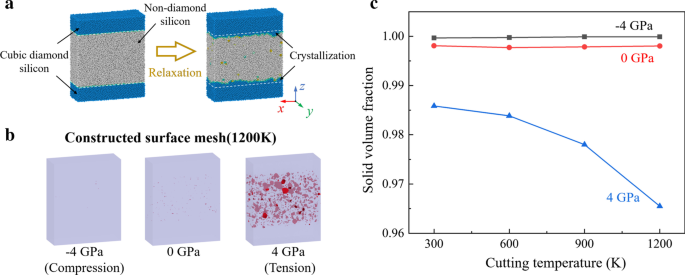
Relaxation simulation of silicon. а Scheme of MD relaxation simulation. б The surface mesh of the relaxed model at 1200 K. c The solid volume fraction curves

Выводы

In this paper, MD simulation is carried out to investigate the cutting mechanism of hybrid machining (HM) process. A modified cutting model is applied to reveal the material removal behavior and subsurface damage formation in one vibration cycle. The main conclusions were as follows:

1. (1)

   During HM process, the dominant material removal mechanism could transform from extrusion to shear in a single vibration cycle. With an increase of the cutting temperature, the generation and propagation of cracks can be effectively suppressed. However, the swelling appears when the dominant material removal mechanism becomes shearing, which is caused by the rotation of the crystal grains in workpiece.

2. (2)

   Based on the stress analysis, the dominant formation mechanism of the subsurface damage in one vibration cycle can be distinct. In the extrusion stage, the subsurface damage can be generated by the shear stress in the damage region. While in the shearing stage, tensile stress becomes dominant in subsurface damage formation. When the cutting temperature is increased, although the tensile stress concentration in the subsurface workpiece is still obvious, the peak value of the stresses is apparently decreased, which effectively suppress the cracks and fractures in workpiece.

3. (3)

   When the cutting temperature is increased, less subsurface damage is generated in the workpiece. However, due to the tensile stress, some vacancies can be generated in the workpiece when the cutting temperature is increased. Therefore, the desired cutting temperature during HM process should be lower than that in ordinary TAC and the vibration parameters should be set carefully to suppress the vacancies in the subsurface workpiece.

Доступность данных и материалов

The datasets used and analyzed in the current study can be obtained from the corresponding authors upon reasonable request.

Сокращения

TAC:

Thermal assisted cutting

VAC:

Vibration assisted cutting

LVC:

Linear vibration cutting

EVC:

Elliptical vibration cutting

DOC:

Depth of cut

HM:

Hybrid machining

FEM:

Метод конечных элементов

MD:

Молекулярная динамика

LAMMPS:

Крупномасштабный массово-параллельный симулятор атомно-молекулярного моделирования

MEAM:

Modified embedded-atom method

SW:

Stillinger–Weber

COMB:

Charge optimized many-body

ABOP:

Analytical bond-order potential

Si-II:

Metallic stable phase

HPPT:

High-pressure phase transition

CNA:

Common neighbor analysis

a-Si:

Amorphous phase

Si-I:

Single-crystal silicon phase

FCC:

Face Center Cubic

CRSS:

Critical resolved shear stress