Морфологическая эволюция подложек Si с ямчатым рисунком (001) под действием снижения поверхностной энергии
Аннотация
Боковое упорядочение гетероэпитаксиальных островков может быть удобно достигнуто за счет подходящего ямочного рисунка на подложке перед осаждением. Контроль формы, ориентации и размера ямок не является тривиальным делом, поскольку, будучи метастабильными, они могут значительно эволюционировать во время осаждения / отжига. В этой статье мы используем модель континуума для изучения типичных морфологий метастабильных ям, которые можно ожидать на Si (001), в зависимости от начальной глубины / формы. Эволюция предсказывается с использованием модели поверхностной диффузии, сформулированной в рамках фазового поля и учитывающей анизотропию поверхностной энергии. Показано, что результаты хорошо воспроизводят типичные метастабильные формы, описанные в литературе. Более того, было обнаружено, что эволюция профилей ям с разной глубиной в долгосрочном масштабе происходит по сходному кинетическому пути. Модель также используется для рассмотрения случая гетероэпитаксиального роста с участием двух материалов, характеризующихся разными гранями в их равновесной форме Вульфа. Это может привести к значительным изменениям морфологии, таким как вращение ямы во время осаждения, что подтверждается экспериментами с Ge / Si.
Фон
Гетероэпитаксия с рассогласованием решеток нескольких полупроводников (таких как Ge / Si или InGaAs / GaAs) может привести к образованию трехмерных островков в соответствии с режимом роста Странски-Крастанова (SK). Хотя возможность получения таких точек путем чистой самосборки [1, 2] особенно привлекательна и вызвала широкий интерес, вскоре стало понятно, что случайное зародышеобразование может серьезно затруднить приложения, наряду с разбросом по размеру и форме.
Десятилетия исследований привели к развитию широкого спектра методов, управляющих гетероэпитаксиальным ростом в направлении формирования упорядоченных структур [3–7]. Среди них было продемонстрировано, что использование подложек с ямчатым рисунком является одним из наиболее универсальных методов для достижения высокого порядка и контроля размера гетероэпитаксиальных островков [8–15].
Подложки с точечным рисунком обычно изготавливаются с помощью таких методов, как литография наноимпринтов [16–18], литография электронным пучком [13, 14] в сочетании с реактивным ионным травлением (RIE) [19, 20] или влажным химическим травлением [21, 20]. 22] и наноиндентированием [23, 24], т.е. нисходящими подходами. С помощью этих методов упорядоченные структуры ямок разрабатываются с высокой точностью и при надлежащих условиях роста [14, 25] приводят к почти идеальному латеральному упорядочению.
Поскольку фактическая форма ямок действительно влияет на энергию системы и, в более общем смысле, на зарождение островков [26, 27], очень важно контролировать их морфологию. Это нетривиально:в конце концов, ямки - это просто просверленные отверстия в подложке. Таким образом, ожидается, что при достаточно высоких температурах капиллярность [28] вызовет морфологическую эволюцию, которая в конечном итоге приведет к полному заживлению. На самом деле, для получения воспроизводимых, долгоживущих метастабильных форм часто используются процессы отжига или дальнейшего осаждения материала подложки после первоначального образования ямок [8, 26]. Обратите внимание, что даже когда ямка стабилизируется по форме, дальнейшая эволюция может происходить во время реальной гетероэпитаксии [29, 30].
В этой работе мы стремимся описать эволюцию подложек с ямчатым рисунком, обусловленную снижением поверхностной энергии за счет поверхностной диффузии. Мы применяем подходящий подход фазового поля [31], позволяющий моделировать масштабы длины и времени, совместимые с экспериментальными [32]. Модель уже была принята для учета ограниченной диффузии кинетики во время морфологической эволюции в гетероэпитаксиальных системах [33–36]. Более того, было показано, что он правильно описывает эволюцию к равновесию, включая реалистичные анизотропные поверхностные энергии [37–39].
Не умаляя общности, мы сосредоточимся на соответствующих случаях ямчатых поверхностей Si (001), широко исследованных в литературе [8, 10, 14, 30, 40, 41].
Работа организована следующим образом. В разделе «Модель фазового поля» мы кратко проиллюстрируем модель фазового поля, используемую для описания эволюции посредством поверхностной диффузии, включая анизотропную поверхностную энергию. Кроме того, мы описываем, как реальная форма Si Wulff учитывается в рассматриваемом подходе. В разделе «Сглаживание ямок Si (001)» ожидаемое сглаживание ямок Si (001), вызванное уменьшением поверхностной энергии, обсуждается путем рассмотрения различных начальных конфигураций, намечая кинетический путь к равновесию. В разделе «Имитация изменения формы из-за чрезмерного роста Ge» рассматривается применение метода к конкретному случаю гетероэпитаксиального роста, который соответствует изменению формы под действием поверхностной энергии при нанесении тонкого слоя Ge на ямку Si. Выводы и замечания кратко изложены в разделе «Выводы».
Методы
Модель фазового поля
Модель фазового поля рассматривает непрерывный параметр порядка φ , в диапазоне φ =1 (сплошной) и φ =0 (вакуум) [31, 32]. Подход основан на функционале энергии [37],
$$ \ begin {align} F =&\ int _ {\ Omega} \ gamma (\ hat {\ mathbf {n}}) \ left (\ frac {\ epsilon} {2} | \ nabla \ varphi | ^ {2 } + \ frac {1} {\ epsilon} B (\ varphi) \ right) d \ mathbf {r} + \\ &+ \ int _ {\ Omega} \ frac {\ beta} {2 \ epsilon} \ left ( - \ epsilon \ nabla ^ {2} \ varphi + \ frac {1} {\ epsilon} B '(\ varphi) \ right) ^ {2} d \ mathbf {r}, \ end {align} $$ (1)с \ (\ Omega \ in \ mathbb {R} ^ {3} \) область определения φ ( г ) и r =( x , y , z ). Первый член соответствует энергии границы раздела фаз в пределах области диффузной границы раздела, определяемой как φ , т.е. к поверхностной энергии твердой фазы. \ (\ gamma (\ hat {\ mathbf {n}}) \) - плотность энергии поверхности, с \ (\ hat {\ mathbf {n}} \) нормалью к поверхности, направленной наружу, и ε толщина границы раздела фаз. Б ( φ ) =18 φ 2 (1− φ ) 2 - двухъямный потенциал с минимумом в φ =0 и φ =1, как в работе. [31]. Второй член в формуле. (1) - это регуляризация Уиллмора, которая требуется в режиме сильной анизотропии, чтобы избежать образования острых углов [37, 38, 42]. β - параметр, соответствующий закруглению угла.
Эволюция φ воспроизводит ограниченную диффузией кинетику поверхностей и задается вырожденной моделью Кана-Хилларда, т. е.
$$ \ frac {\ partial \ varphi} {\ partial t} =D \ nabla \ left [M (\ varphi) \ nabla \ mu \ right], $$ (2)где μ = δ F / δ φ - химический потенциал, D - коэффициент диффузии, а M ( φ ) =(36 / ε ) φ 2 (1− φ ) 2 - функция подвижности, ограниченная поверхностью. Уравнение для μ читает
$$ \ begin {align} g (\ varphi) \ mu =\ delta F / \ delta \ varphi =&- \ epsilon \ nabla \ cdot \ left [\ gamma (\ hat {\ mathbf {n}}) \ nabla \ varphi \ right] + \ frac {1} {\ epsilon} \ gamma (\ hat {\ mathbf {n}}) B '(\ varphi) + \\ &- \ epsilon \ nabla \ cdot \ left [| \ nabla \ varphi | ^ {2} \ nabla _ {\ nabla \ varphi} \ gamma (\ hat {\ mathbf {n}}) \ right] + \\ &+ \ beta \ left (- \ nabla ^ {2} \ каппа + \ гидроразрыв {1} {\ epsilon ^ {2}} B ^ {\ prime \ prime} (\ varphi) \ kappa \ right), \ end {align} $$ (3)с κ =- ε ∇ 2 φ + (1 / ε ) B ′ ( φ ) и g ( φ ) =30 φ 2 (1− φ ) 2 [33, 37, 38]. Последняя является стабилизирующей функцией, которая обеспечивает сходимость второго порядка по толщине границы раздела, не влияя на описание переноса материала посредством поверхностной диффузии [43, 44]. Профиль в направлении, перпендикулярном границе раздела в состоянии равновесия, хорошо описывается
$$ \ varphi (\ mathbf {r}) =\ frac {1} {2} \ left [1- \ tanh \ left (\ frac {3 d (\ mathbf {r})} {\ epsilon} \ right) \ right], $$ (4)где d ( г ) - это расстояние со знаком до центра границы раздела фаз. Это уравнение используется для задания начального условия для φ как указано ниже. Мы называем поверхность твердой фазы φ ∼0.5 изоповерхность. Все геометрические свойства рассматриваемой поверхности могут быть получены из φ , например, направленная наружу нормаль поверхности \ (\ hat {\ mathbf {n}} =- \ nabla \ varphi / | \ nabla \ varphi | \).
Анизотропная поверхностная энергия
Чтобы описать анизотропные поверхностные энергии, мы рассмотрели определение плотности поверхностной энергии, \ (\ gamma (\ hat {\ mathbf {n}}) \), как введено в [38, 39]:
$$ \ gamma (\ hat {\ mathbf {n}}) =\ gamma_ {0} \ left (1- \ sum_ {i} ^ {N} \ alpha_ {i} \ left (\ hat {\ mathbf {n }} \ cdot \ hat {\ mathbf {m}} _ {i} \ right) ^ {w_ {i}} \ Theta \ left (\ hat {\ mathbf {n}} \ cdot \ hat {\ mathbf {m }} _ {i} \ right) \ right). $$ (5)где предпочтительные ориентации \ (\ hat {\ mathbf {m}} _ {i} \), т. е. направления, вдоль которых плотность поверхностной энергии имеет минимум, могут быть произвольно заданы вместе с их относительной глубиной, α я , относительно γ 0 . Параметры w я контролировать протяженность областей, где \ (\ gamma (\ hat {\ mathbf {n}}) <\ gamma _ {0} \), вокруг м я это и есть ширина минимумов (см. также [38]).
Чтобы учесть специфическую анизотропию кристаллов Si, мы установили направления минимальной энергии, m я , соответствующие 〈001〉, 〈113〉, 〈110〉 и 〈111〉 [45]. α я коэффициенты, определяющие глубину минимумов, получены по [39]
$$ \ alpha_ {i} =1- \ left (\ frac {\ gamma_ {i}} {\ gamma _ {\ langle 001 \ rangle}} \ right) \ left (1- \ alpha _ {\ langle 001 \ rangle} \ справа), $$ (6)где α 〈001〉 =0,15 устанавливается в качестве эталона, а различные γ я соответствуют значениям поверхностной энергии вышеупомянутых ориентаций, как сообщается в [4]. [45]. Без ограничения общности положим γ 0 =1. Действительно, отношения минимумов и силу анизотропии можно контролировать с помощью α я значения из уравнения. (6) и α 〈001〉 , а γ 0 играет роль префактора в уравнении. (2), влияя, таким образом, только на абсолютный временной масштаб эволюции.
Ширина минимумов энергии в уравнении. (5) установлены на w я =50 для всех направлений минимумов, кроме w 〈113〉 =100 [39]. Согласно этому определению параметров, острые углы предсказываются в форме Вульфа, т.е. анизотропия поверхностной энергии является «сильной» [38, 42, 46]. Следовательно, регуляризация Уиллмора строго необходима для выполнения моделирования. β value устанавливает расширение закругленной области по углам, которые, как известно, имеют радиус, пропорциональный \ (\ sqrt {\ beta} \) [37]. Чтобы выполнить моделирование, масштаб длины, установленный закруглением угла на β должно быть больше разрешения пространственной дискретизации численного метода. Однако стоит отметить, что маленькие фасеты, которые могут присутствовать в форме Вульфа с расширением в порядке \ (\ sqrt {\ beta} \), могут быть скрыты при использовании слишком большого β значения, а также мелкомасштабная огранка, включающая предпочтительные ориентации, фактически присутствующие в форме Вульфа. В этой работе мы устанавливаем β =0,005. В соответствии с размером области моделирования, указанным ниже, это значение позволяет нам принять возможную пространственную дискретизацию. Более того, все предпочтительные ориентации, входящие в уравнения. (5) и (6) воспроизводятся. С другой стороны, возможная огранка с меньшим масштабом, чем ∼0,07, не может быть воспроизведена из-за расширения скругления угла.
Начальная настройка морфологии и моделирования
Чтобы исследовать любую морфологическую эволюцию с помощью модели фазового поля, определенной в этом разделе, правильное начальное условие для φ должен быть установлен. Здесь мы рассматриваем гладкую геометрию ямы, вырезанную на плоской поверхности (001), с системой отсчета, установленной на \ (\ hat {\ mathbf {x}} =\, [\! 100] \), \ (\ hat {\ mathbf {y}} =\, [\! 010] \) и \ (\ hat {\ mathbf {z}} =\, [\! 001] \). В частности, мы рассматриваем круговую поверхность (001) с радиусом L на высоте h 0 - H , плавно соединенный с окружающей (001) плоской поверхностью на высоте h 0 . Такая геометрия задается как начальное условие для φ используя уравнение. (4) с d ( г ) знаковое расстояние от поверхности Γ ( x , y ) определяется
$$ \ Gamma (x, y) =\ left \ {\ begin {align} h_ {0} - &H &\ qquad r \ leq L \\ h_ {0} - &H \ exp \ left [- \ frac {1} {2} \ frac {| \ mathbf {s} - \ bar {\ mathbf {s}} | ^ {2}} {\ sigma ^ {2}} \ right] &\ qquad r> L \ end {выровнено} \ право. $$ (7)с \ (r =\ sqrt {x ^ {2} + y ^ {2}} \) и
$$ \ mathbf {s} =(x, y), \ qquad \ bar {\ mathbf {s}} =\ frac {R} {r} (x, y). $$ (8)R = H / 4 L определяется как параметр соотношения сторон, а σ - параметр, контролирующий протяженность непрерывной связи между дном котлована и окружающей его плоской областью. Этот параметр установлен здесь на σ = L / 2.
На рис. 1 начальное условие, принятое для φ проиллюстрировано. На рисунке 1а показан Γ ( x , 0) профили с разными значениями R . На рисунке 1b показано определение φ . с помощью уравнения. (4) в области трехмерного параллелепипеда. В частности, на этой панели показано поперечное сечение, проходящее через центр всего домена. В левой части показана область, соответствующая твердой фазе, т.е. область, где φ > 0,5, выявляя поверхность, соответствующую исходной морфологии ямки. Правая часть показывает значения φ . во всей трехмерной области, т.е. в объемных фазах и в непрерывном переходе между ними.
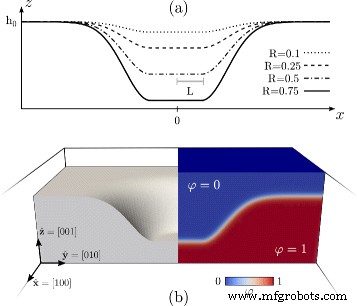
Начальное условие для модели фазового поля, напоминающей гладкую ямку на поверхности (001) твердой пленки. а Γ ( x , 0) профили из уравнения. (7) получено для разных R ценности. б Определение φ в трехмерной области, принятой для численного моделирования. Это получается из уравнения. (4) с d ( г ) знаковое расстояние от Γ ( x , y ) с R =0,5. Слева твердая фаза, где φ Показано> 0,5. Справа цветная карта, показывающая φ в 3D-домене сообщается
Численное моделирование выполняется для интегрирования уравнений. (2) и (3). Они выполняются с использованием набора инструментов AMDiS [47, 48], метода конечных элементов (FEM), с полунявной схемой интегрирования и уточнением сетки на интерфейсе [33, 38, 49]. Периодические граничные условия устанавливаются по направлениям \ (\ hat {\ mathbf {x}} \) и \ (\ hat {\ mathbf {y}} \). Граничные условия отсутствия потока (Неймана) устанавливаются вверху и внизу области моделирования вдоль направления \ (\ hat {\ mathbf {z}} \). Масштаб времени эволюции масштабируется с коэффициентом 1 / D , что соответствует набору D =1. Далее мы говорим о времени моделирования в произвольных единицах. Размер ямы произвольно установлен на L . =1, а толщина интерфейса установлена на ε =0,2
Результаты и обсуждение
Сглаживание ямок Si (001)
В этом разделе мы проиллюстрируем результаты, касающиеся морфологических изменений в процессе эволюции подложек Si (001) с ямчатым рисунком. Описанная выше модель позволяет описать конкретный случай кремния посредством определения анизотропной поверхностной энергии, как в разделе «Анизотропная поверхностная энергия». Мы ожидаем, что следующие результаты будут справедливы с качественной точки зрения для любого размера, при условии, что система достаточно велика, чтобы принять континуальный подход (\ (\ gtrsim 10 \) нм) [32], и форма может быть параметризована следующим образом:соотношение сторон R аналогично рис. 1 а. Реальный масштаб длины можно учесть, установив L параметр к соответствующему в реальных единицах, L г . Затем шкала реального времени может быть описана с учетом реальных значений D и γ 0 и умножая на L г длина, т.е. путем масштабирования на L г / L с L унитарный, как указано выше.
Сначала остановимся на первых этапах эволюции. Начальное условие, установленное формулой. (7) состоит из профиля, поверхность которого не имеет преимущественной ориентации. При рассмотрении эволюции за счет поверхностной диффузии, вызванной уменьшением анизотропной поверхностной энергии, ожидается огранка исходного профиля. Это проиллюстрировано на рис. 2, где огранка двух профилей с R =0,25 на рис. 2а и R =0,5 на рис. 2б. Цветовая шкала показывает значения \ (\ gamma (\ hat {\ mathbf {n}}) \) на поверхности. Это позволяет идентифицировать грани как области с почти однородной плотностью поверхностной энергии, соответствующей минимумам уравнения (2). (5), ограниченный локализованными областями с высокими значениями \ (\ gamma (\ hat {\ mathbf {n}}) \). В зависимости от исходного соотношения сторон ямы формируются разные грани. Для меньшего R грань (001) внизу сохраняется, принимая квадратную форму. Края ямки ограничены четырьмя гранями {113}, соединенными небольшими гранями треугольной формы {110}. Согласно большему соотношению сторон, большая граненая поверхность присутствует при рассмотрении R =0,5, что учитывает появление преимущественных ориентаций с большим наклоном по отношению к поверхности (001). В частности, исходная форма допускает наличие граней {111}, образующихся между двумя гранями {113} вблизи дна и плоской области. Между ними образуются широкие {110} грани.
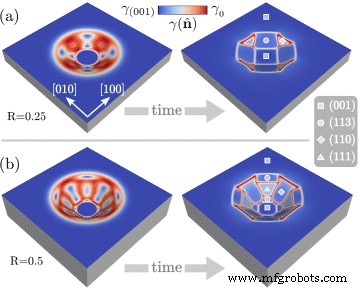
Фацетирование исходного профиля, как определено в разделе «Начальная морфология и настройка моделирования», в соответствии с поверхностной диффузией и \ (\ gamma (\ hat {\ mathbf {n}}) \), воспроизводящей поверхностную энергию Si. Рассмотрены две различные исходные морфологии: a R =0,25 и b R =0,5. На фасетных морфологиях используются символы для обозначения семейств фасетов. Цветовая шкала показывает значения \ (\ gamma (\ hat {\ mathbf {n}}) \) на поверхности
Результаты, представленные на рис. 2, показывают возможность прогнозирования морфологии фасеточных ямок в соответствии с соотношением сторон или, в целом, в соответствии с исходной морфологией. Теперь мы исследуем также динамику в долгосрочном масштабе, исследуя морфологическую эволюцию до равновесия [38]. Это проиллюстрировано на рис. 3, где мы сосредоточены на самой глубокой яме, рассмотренной до сих пор, то есть с R =0,5, и показаны основные морфологические изменения. В частности, перспективные изображения и виды сверху различных морфологий, полученные в ходе эволюции, представлены на рис. 3 a, b, соответственно. На первом этапе этого моделирования мы наблюдаем исчезновение самых крутых граней {111} и увеличение соседних граней {113}. Затем последние сливаются и начинается усадка граней {110}. Обнаружено, что они исчезают на более поздних стадиях после принятия треугольной формы, придавая яме квадратный очертание при виде сверху. Кроме того, со временем исчезают грани {113} и достигается глобальное выравнивание. Масштаб реального времени, полученный в этом моделировании, можно оценить с помощью литературных данных. В частности, мы можем рассматривать D определяется законом Аррениуса с префактором и энергией активации из работы. [50], где также учтены тепловые флуктуации. γ 0 установлено значение \ (\ gamma (\ hat {\ mathbf {n}}) \ sim 8.7 \) эВ / нм 2 когда \ (\ hat {\ mathbf {n}} =(001) \) [51] из уравнения. (5), то есть γ 0 =10,2 эВ / нм 2 . Другие зависящие от материала коэффициенты поверхностной диффузии [28], т. Е. Атомный объем и плотность на поверхности, устанавливаются для воспроизведения случая Si. Согласно этим значениям ожидаемая продолжительность всего процесса при высокой температуре T ∼1100−1200 ° C для L г десятки нанометров - это часы.
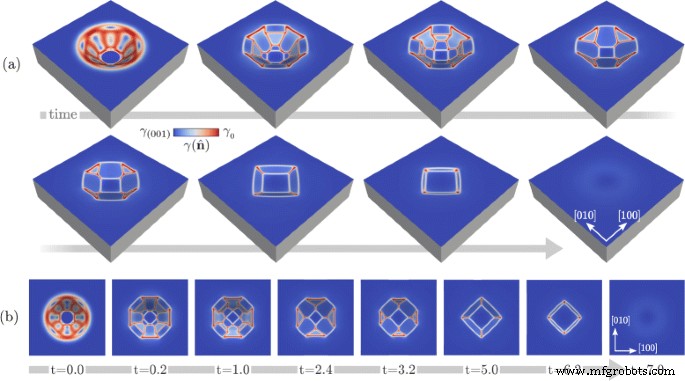
Эволюция к равновесию для кармана Si, имеющего исходную морфологию, как на рис. 2b. а Перспективный вид, показывающий основные морфологические изменения. б Морфология на панели a , вид сверху . Время указано на панели b . выражается в условных единицах. Цветовая шкала показывает значения \ (\ gamma (\ hat {\ mathbf {n}}) \) на поверхности
Наряду со специфическими морфологическими изменениями, происходящими в процессе эволюции, следует отметить две основные особенности. Во-первых, эволюция приводит к ожидаемому глобальному уплощению поверхности, и это происходит с постепенным исчезновением крутых граней, заменяемых более мелкими. Хотя такое поведение может быть выведено только из аргументов о минимизации энергии и понижении соотношения сторон, стоит отметить, что здесь представлена полная эволюция, касающаяся наличия подобных граней, но с разными относительными размерами. Это согласуется с тем фактом, что морфологии, полученные в ходе эволюции, соответствуют неравновесным конфигурациям и определяют путь к глобальному минимуму энергии. Тогда, несмотря на то, что ожидаемые грани и их энергия известны, конкретная морфология в определенный момент эволюции может быть описана только с учетом динамики, а не только с учетом минимизации глобальной энергии [38].
Второй важный момент, показанный результатами, представленными на рис. 3, касается промежуточных стадий. Когда форма в процессе эволюции приближается к геометрии с глубиной, подобной исходному профилю, полученному с помощью R =0,25, т.е. при t ~ 3.2, морфология, вызванная минимизацией энергии, очень похожа на то, что показано на рис. 2b, даже если начинать с начальной конфигурации со значительной разницей в глубине (в данном случае - двойной). Это говорит о существовании общего кинетического пути к окончательному уплощению, который достигается после первой быстрой огранки исходной морфологии. Этот аргумент фактически подтверждается и дополнительно проиллюстрирован на графиках на рис. 4. Здесь сообщается о монотонном спаде энергии во время эволюции после начальной огранки при рассмотрении ямок с R равны 0,1, 0,25, 0,5 и 0,75, как на рис. 1а. На рис. 4а рассматривается масштаб времени, выраженный в условных единицах. На рис. 4b представлены те же изменения энергии с соответствующим сдвигом шкалы времени, что подчеркивает сходное затухание энергии при приближении к аналогичным соотношениям сторон структуры. \ (t ^ {*} _ {R} \) определяется как время получения плоской поверхности, т. е. время достижения глобального минимума энергии, которое отличается для каждого моделирования, как показано на рис. 4 а. Как показано на этом графике, спады энергии почти перекрываются для R ≤0,5. Очень небольшая разница наблюдается только при рассмотрении R =0,75, результаты спада энергии которых все еще очень близки к другим кривым, и различия в основном исчезают при \ (t \ gtrsim 5.0 \). Стоит отметить, что при больших отклонениях от начальной конфигурации, а именно при R ≫1, такие геометрии могут развиваться по-разному, с разными эффектами на шкалы времени и морфологии [52, 53]. Более того, известно, что топологические изменения происходят в крайних случаях, например, при очень глубоких траншеях, предотвращающих возможность достижения глобального равновесия с плоской поверхностью (001) [34, 39, 54].
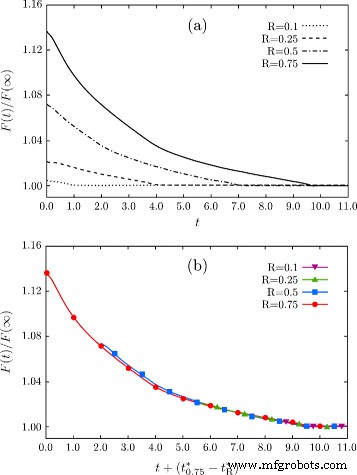
Уменьшение энергии в процессе изменения геометрии карьера. а F ( т ), нормированная на энергию плоской поверхности (001), полученную на заключительном этапе эволюции. Спад энергии, полученный в результате моделирования с разными значениями R для исходного профиля, а именно из R =От 0,1 до R =0,75. Время выражается в произвольных единицах. б Кривые как на панели a сдвинуто, чтобы соответствовать \ (t_ {R} ^ {*} \), то есть времени, за которое достигается глобальное выравнивание ямы, в зависимости от R
Формы, полученные при моделировании, описанном в этих разделах, будут наблюдаться в экспериментах, в частности, когда обработка включает условия, близкие к термодинамическому пределу. Некоторые из морфологий, представленных на рис. 3, действительно соответствуют очертаниям подложек Si (001) с ямчатым рисунком. Например, морфология, состоящая из широкой поверхности (001), ограниченной узкими гранями {113}, как на рис. 3 в точке t При рассмотрении подложек Si (001) с ямчатым рисунком и соотношением сторон 0,05 < R наблюдаются ~ 5,0. <0,1, как в работе. [10, 30]. Кроме того, относительная протяженность граней на вышеупомянутом этапе моделирования на фиг. 3 очень похожа на то, что было сообщено в этих экспериментальных работах. Это согласие между моделированием и экспериментом дополнительно оценивает теоретическое описание поверхностной диффузии, принятое здесь. Однако мы сосредоточились на общих особенностях процесса, и более подробное сравнение с конкретными экспериментами выходит за рамки настоящей работы.
Имитация изменения формы из-за чрезмерного роста Ge
Как упоминалось во введении, одним из основных применений шаблонов Si с ямчатым рисунком является контроль роста самоорганизующихся островков [55]. Это особенно верно при рассмотрении расположения Ge или Si 1 - c Ge c островков на подложках Si (001) [6]. С помощью методологии, принятой в предыдущем разделе, мы можем исследовать морфологические изменения, связанные с особенностями поверхностной энергии. Следовательно, начиная с правильной начальной конфигурации, напоминающей реальную морфологию кармана Si, и учитывая различия в плотности поверхностной энергии, ожидаемые при нанесении другого материала, мы можем предсказать, каков будет соответствующий вклад в морфологические изменения.
В данном случае тематическое исследование состоит в разрастании Ge над подложкой из Si (001) с ямчатым рисунком с аспектным отношением, близким к 0,1. Профиль на рис. 3 в t =5.0 считается исходной морфологией. Затем задается поверхностная энергия, включающая также минимумы по направлениям 〈105〉. Это определение \ (\ gamma (\ hat {\ mathbf {n}}) \) имитирует наличие самой любимой ориентации с малым уклоном в системах Ge / Si (001) [56–58]. Высокая стабильность граней {105} обусловлена взаимодействием между реконструкцией поверхности и эффектами деформации, связанными с рассогласованием решеток между эпитаксиальным слоем и подложкой [59–61]. Значение плотности поверхностной энергии, которое необходимо использовать в уравнении. (6) взято из работы. [58] в пределе толстого слоя Ge. Обратите внимание, что другие грани, у которых поверхностная энергия ближе к (001), например {1 1 10}, здесь не учитываются. Поскольку углы между направлениями 〈105〉 и [001] очень малы, w я параметры больше, чем те, которые были приняты ранее, необходимы для правильного описания минимумов энергии уравнения. (5) [38]. В частности, мы устанавливаем w {105} = w {001} =500.
На рис. 5 показана эволюция за счет поверхностной диффузии с новым определением \ (\ gamma (\ hat {\ mathbf {n}}) \). На рис. 5а показана морфологическая эволюция поверхности при увеличении z . - ось в 5 раз. На первых этапах грани {105} образуются между гранями {113}, присутствующими в исходном профиле. Поскольку ориентации 〈105〉 имеют минимальную энергию, как также показано на рис. 5b, соответствующие грани расширяются, а грани {113} сжимаются. На более поздних этапах образуется яма, ограниченная только фасетками {105}, с все еще поверхностью (001) на дне. При виде сверху, как на рис. 5б, изменение морфологии приводит к повороту контура ямы на 45 °. Это действительно наблюдается при осаждении Ge на подложки с рисунком Si в экспериментах [41] или при спонтанном росте ямок из-за дефектов или примесей [40]. Также обнаружено, что образование фасеток {105} является предпочтительным местом зародышеобразования для дальнейшего роста точек Ge [30]. Эволюция, показанная на рис. 5, демонстрирует, что изменение формы, ведущее к повороту контура ямы, может быть достигнуто только за счет уменьшения поверхностной энергии. Ожидается, что это будет реальная ситуация в условиях, близких к равновесию, когда в термодинамических движущих силах доминируют поверхностные вклады, то есть для малых объемов Ge. Фактически, чтобы полностью описать процесс, необходимо включить эффекты упругости, перемешивание и рост твердой фазы [32]. Также стоит упомянуть, что в экспериментах используются даже более мелкие ямы Si, показывающие грани с нормалями вдоль {11 n } направлений, с 5 < n <10 [41] (т. Е. {1 1 10} фасетов). Геометрия ямы, ограниченная этими гранями, приведет к аналогичной эволюции, поскольку они соответствуют той, которая принята в качестве начальной конфигурации на рис. 4, только с меньшим наклоном по отношению к плоскости (001).
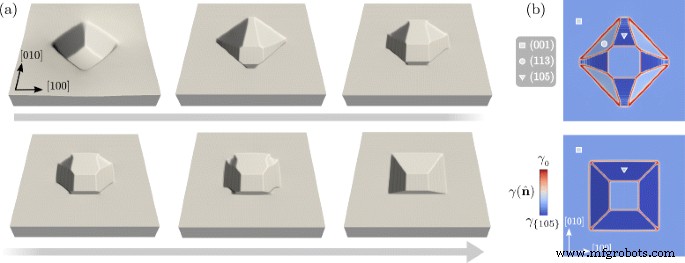
Эволюция профиля на рис. 3 при t =5.0, с определением поверхностной энергии, включая ориентации 〈105〉. а Профили поверхности на репрезентативных стадиях эволюции в сторону образования ямы, ограниченной только гранями {105}. г ось увеличена в 5 раз. b Вид сверху, показывающий значения \ (\ gamma (\ hat {\ mathbf {n}}) \) на поверхности. Второй и последний этапы панели а сообщаются в верхней и нижней части соответственно. Символы на рис. 2 используются для обозначения различных семейств фасетов
Выводы
В этой работе мы использовали модель континуума, основанную на поверхностной диффузии, для исследования временной эволюции ямок, выкопанных в подложке Si (001). Путем подходящего решения (сильной) анизотропии поверхностной энергии с параметризацией, основанной на хорошо известной форме Си Вульфа, мы предсказали типичные метастабильные конфигурации в соответствии с экспериментами, включая случай, когда осаждение другого материала вводит новые стабильные грани. The entire evolution towards the global flattening of the pit has been illustrated, and it is found to follow the same kinetic pathway also when considering pits with different initial depths. We believe that the model can be predictive also for initial configurations strongly deviating from the ones which we have analyzed as examples. As a consequence, the present approach can be useful in designing experiments based on still-unexplored pit shapes. Furthermore, the model is general and can be easily adapted to different substrates upon re-parametrizing the surface energy.
Наноматериалы
- Отверждаемые светодиодами конформные покрытия формируют зеленую эволюцию
- Перспективы эволюции Arduino
- Форма машинного винта
- MoS2 с контролируемой толщиной для электрокаталитического выделения водорода
- Раскрытие морфологической эволюции и кинетики травления пористых кремниевых нанопроволок во время химическ…
- Электроформование на изоляционные основы путем контроля смачиваемости и влажности поверхности
- Колебания состояния окисления церия, вызванные диффузией кислорода в коллоидных наноцериях (CeO2 - x)
- Изготовление тонких пленок SrGe2 на подложках Ge (100), (110) и (111)
- Гибкая подложка
- Эволюция трехмерного зрения



