Решение Minterm и Maxterm

До сих пор мы находим решения проблем логической редукции на основе суммы произведений (SOP). Для каждого из этих SOP-решений существует также решение Product-Of-Sums (POS), которое может быть более полезным в зависимости от приложения.

Перед тем, как приступить к работе над решением «произведение сумм», нам нужно ввести новую терминологию. Приведенная ниже процедура сопоставления терминов продуктов не нова в этой главе.

Мы просто хотим установить формальную процедуру для minterms для сравнения с новой процедурой для maxterms.

Минтерм

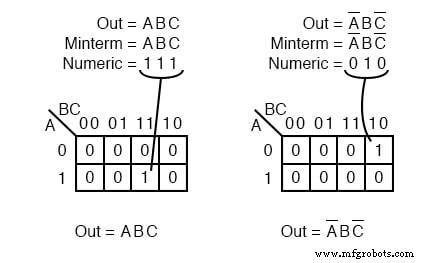
минтерм является логическим выражением, результатом которого является 1 для вывода отдельной ячейки и 0 s для всех других ячеек в карте Карно или таблице истинности. Если в minterm есть один 1 а остальные ячейки как 0 s, он должен покрывать минимальную площадь 1 с.

На иллюстрации вверху слева показан термин ABC . , один термин продукта, как один 1 на карте, которая в противном случае имеет значение 0 с. Мы не показали 0 s на наших картах Карно до этого момента, поскольку их принято опускать без особой необходимости. Другой минтерм A’BC ’ показан вверху справа.

Важно отметить, что адрес ячейки напрямую соответствует отображаемому minterm. То есть ячейка 111 соответствует minterm ABC вверху слева.

Вверху справа мы видим, что выражение A’BC ’ соответствует непосредственно ячейке 010 . Логическое выражение или карта может иметь несколько минтермов.

Ссылаясь на рисунок выше, давайте резюмируем процедуру размещения минтерма на K-карте:

• Определите термин minterm (термин продукта), который необходимо сопоставить.
• Запишите соответствующее двоичное числовое значение.
• Используйте двоичное значение в качестве адреса для размещения 1 на K-карте
• Повторите шаги для других minterms (P-термины в Sum-Of-Products).

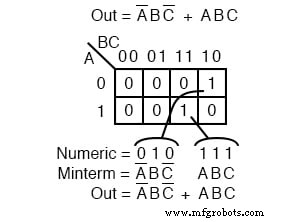
Логическое выражение чаще всего состоит из нескольких минтермов, соответствующих нескольким ячейкам на карте Карно, как показано выше. Несколько минтермов на этой карте - это отдельные минтермы, которые мы рассмотрели на предыдущем рисунке.

Мы рассматриваем для справки, что 1 s выходят из K-карты как адрес двоичной ячейки, который напрямую преобразуется в один или несколько терминов продукта.

Под непосредственно мы подразумеваем, что 0 соответствует дополненной переменной, а 1 соответствует истинной переменной. Пример: 010 . конвертируется напрямую в A’BC ’ .

В этом примере не было снижения. Тем не менее, у нас есть результат «Сумма продуктов» на минтермах.

Ссылаясь на приведенный выше рисунок, давайте резюмируем процедуру написания сокращенного логического уравнения суммы произведений на основе K-карты:

• Сформируйте самые большие группы из 1 Возможны все варианты. Группы должны иметь степень 2.
• Записывать двоичное числовое значение для групп.
• Преобразовать двоичное значение в термин продукта.
• Повторите шаги для других групп. Каждая группа дает р-члены в сумме продуктов.

Пока ничего нового, прописан формальный порядок работы с минтермами. Это служит образцом для работы с maxterms.

Затем мы атакуем логическую функцию, которая равна 0 . для отдельной ячейки и 1 s для всех остальных.

Макстерм

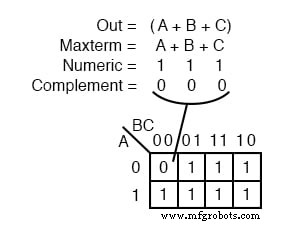
A maxterm является логическим выражением, результатом которого является 0 для вывода выражения одной ячейки и 1 s для всех других ячеек в карте Карно или таблице истинности. На иллюстрации вверху слева показан максимальный срок (A + B + C) , элемент с одной суммой, как один 0 на карте, которая иначе 1 с.

Если maxterm содержит один 0 а остальные ячейки - как 1 s, максимальная площадь покрытия составляет 1 с.

Теперь есть некоторые отличия, потому что мы имеем дело с чем-то новым, maxterms. Максимальный срок - 0 . а не 1 на карте Карно. Maxterm - это сумма, (A + B + C) в нашем примере это не термин продукта. Также выглядит странным, что (A + B + C) отображается в ячейку 000 .

Для уравнения Out =(A + B + C) =0 , все три переменные (A, B, C) по отдельности должно быть равно 0 . Только (0 + 0 + 0) =0 будет равно 0 . Таким образом мы размещаем наш единственный 0 для minterm (A + B + C) в ячейке A, B, C =000 на K-карте, где все входы - 0 .

Это единственный случай, который даст нам 0 для нашего maxterm. Все остальные ячейки содержат 1 s, потому что любые входные значения, кроме ( (0,0,0) для (A + B + C) дает 1 s после оценки.

Ссылаясь на приведенный выше рисунок, процедура размещения maxterm на K-карте следующая:

• Определите термин "Сумма", который нужно сопоставить.
• Запишите соответствующее двоичное числовое значение.
• Сформируйте дополнение
• Используйте дополнение в качестве адреса для размещения 0 на K-карте
• Повторите эти действия для других maxterms (сумма терминов в выражении "произведение сумм").

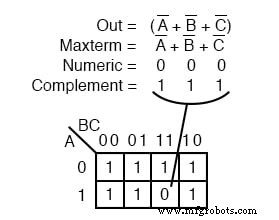
Другой maxterm A ’+ B’ + C ’ показано выше. Числовой 000 соответствует A ’+ B’ + C ’ . Дополнение: 111 . . Разместите 0 для maxterm (A ’+ B’ + C ’) в этой ячейке (1,1,1) K-карты, как показано выше.

Почему следует (A ’+ B’ + C ’) вызвать 0 находиться в ячейке 111 ? Когда A ’+ B’ + C ’ равно (1 ’+ 1’ + 1 ’) , все 1 s в, что равно (0 + 0 + 0) после принятия дополнений у нас есть единственное условие, которое даст нам 0 . Все 1 дополняются до всех 0 s, что равно 0 когда ИЛИ изд.

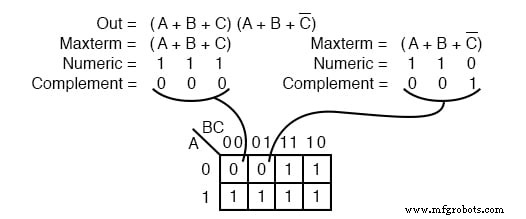
Выражение или карта логического произведения на сумму может иметь несколько maxterms, как показано выше. Maxterm (A + B + C) дает числовой 111 который дополняет до 000 , помещая 0 в ячейке (0,0,0) . Maxterm (A + B + C ’) дает числовой 110 который дополняет 001 , помещая 0 в ячейке (0,0,1) .

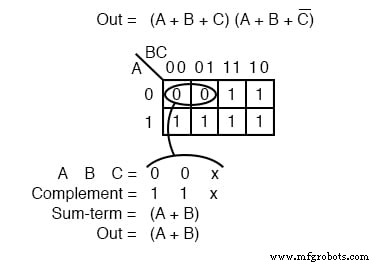
Теперь, когда у нас есть настройка k-map, нас действительно интересует, как написать сокращение произведения сумм. Сформируйте 0 s в группы. Это будет группа из двух человек ниже. Запишите двоичное значение, соответствующее сумме-члену, равному (0,0, X) . .

И A, и B равны 0 . для группы. Но, C оба 0 и 1 поэтому мы пишем X как заполнитель для C . Сформируйте дополнение (1,1, X) . Напишите сумму-член (A + B) отказавшись от C и X который занял свое место.

В общем, ожидайте, что в результате "произведение сумм" будет больше сумм. Хотя у нас есть простой пример.

Подведем итог процедуре написания логической редукции произведения сумм для K-карты:

• Сформируйте самые большие группы из 0 s возможно, покрывая все максимальные сроки. Группы должны иметь степень 2.
• Записать двоичное числовое значение для группы.
• Дополнять двоичное числовое значение для группы.
• Преобразование дополнительного значения в сумму-член.
• Повторите шаги для других групп. Каждая группа дает суммарный член в результате "произведение сумм".

Примеры

Пример:

Упростите приведенное ниже логическое выражение "произведение сумм", предоставив результат в форме POS.

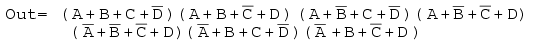
Решение:

Перенесите семь максимальных терминов на карту ниже как 0 . с. Не забудьте дополнить входные переменные при поиске правильного местоположения ячейки.

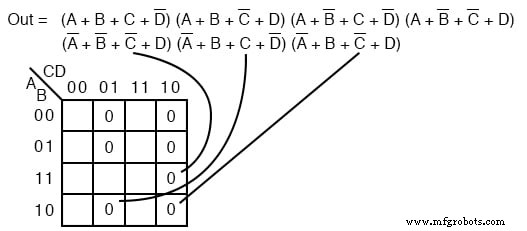
Мы отображаем 0 s, как они отображаются слева направо сверху вниз на карте выше. Мы размещаем последние три maxterms линиями выноски.

Как только ячейки будут размещены выше, сформируйте группы ячеек, как показано ниже. Группы большего размера дадут сумму с меньшим количеством входов. Меньшее количество групп приведет к меньшему количеству сумм в результате.

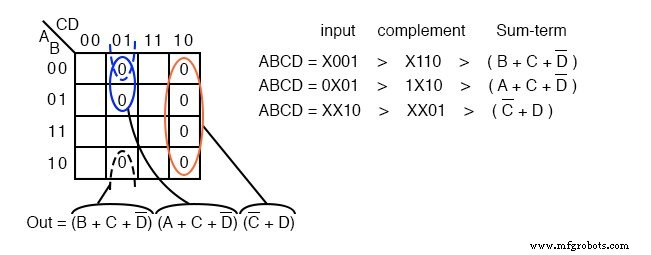
У нас есть три группы, поэтому мы ожидаем, что в нашем POS-результате выше будет три суммы-члена. Группа из 4 ячеек дает сумму с двумя переменными. Две группы по 2 ячейки дают нам две суммы-члена с 3 переменными.

Подробно показано, как мы пришли к Суммарным условиям выше. Для группы напишите адрес входа двоичной группы, затем дополните его, преобразовав его в логический член суммы. Конечный результат - произведение трех сумм.

Пример:

Упростите приведенное ниже логическое выражение "произведение сумм", предоставив результат в форме СОП.

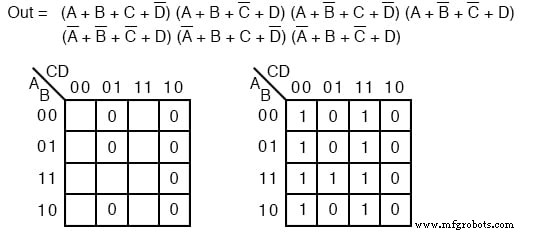
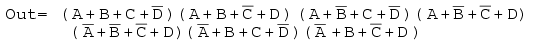
Решение: Это похоже на повторение последней проблемы. За исключением того, что мы запрашиваем решение суммы продуктов вместо продукта сумм, которое мы только что закончили. Сопоставьте максимальный срок 0 s из произведения сумм, заданного как в предыдущей задаче, внизу слева.

Затем введите предполагаемый 1 s в оставшихся ячейках карты справа вверху.

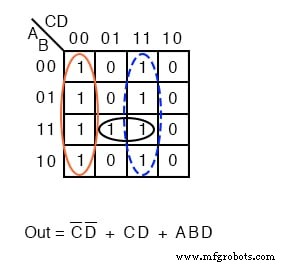
Формируйте группы по 1 s, чтобы охватить все 1 с. Затем напишите упрощенный результат суммы произведений, как в предыдущем разделе этой главы. Это идентично предыдущей проблеме.

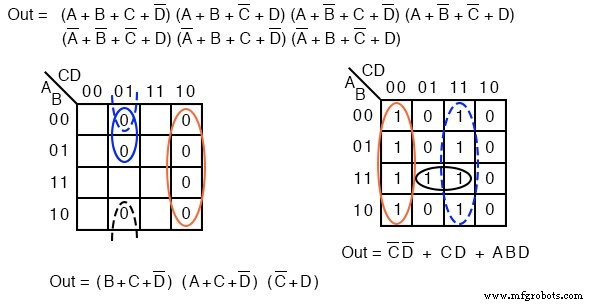
Выше для сравнения показано решение «Произведение сумм» из предыдущего примера и решение «Сумма произведений» из текущей задачи.

Какое решение проще? POS использует ворота 3-И и ворота 1-И, в то время как SOP использует ворота 3-И и 1-ИЛИ. У обоих по четыре ворот.

Присмотревшись, посчитаем количество входов гейта. POS использует 8 входов; СОП использует 7 входов. По определению решения с минимальной стоимостью решение СОП проще.

Это пример технически правильного ответа, от которого мало пользы в реальном мире.

Лучшее решение зависит от сложности и используемого семейства логических схем. Решение SOP обычно лучше, если используется семейство логики TTL, поскольку вентили NAND являются основным строительным блоком, который хорошо работает с реализациями SOP.

С другой стороны, решение POS будет приемлемым при использовании семейства логики CMOS, поскольку доступны все размеры вентилей NOR.

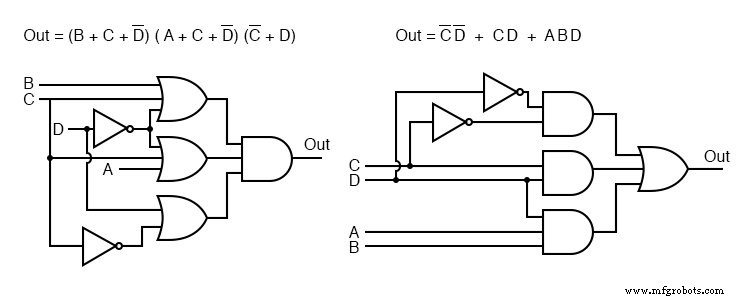
Диаграммы ворот для обоих случаев показаны выше:произведение сумм слева и сумма произведений справа.

Ниже мы более подробно рассмотрим версию нашего примера логики Sum-Of-Products, которая повторяется слева.

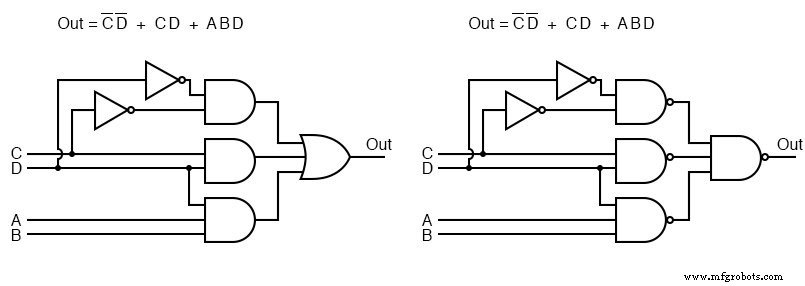
Прежде всего, логические элементы И слева были заменены на элементы И-НЕ справа. Логические элементы ИЛИ на выходе заменены логическими элементами И-НЕ. Чтобы доказать, что логика И-ИЛИ эквивалентна логике И-И-И-НЕ, переместите инвертор инвертирующих пузырей на выходе вентилей 3-И-НЕ на вход конечной И-НЕ, как показано на рисунке сверху справа налево снизу.>

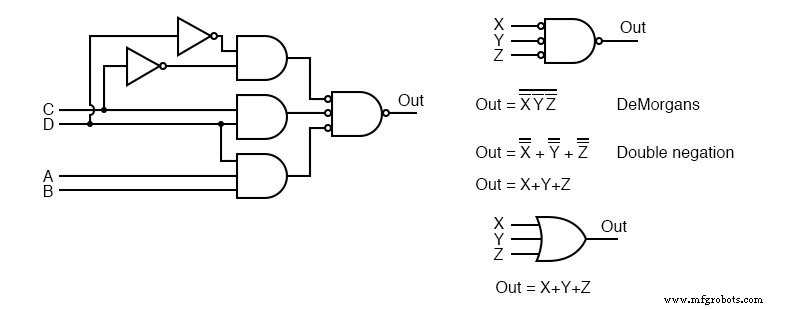
Вверху справа мы видим, что выходной элемент И-НЕ с инвертированными входами логически эквивалентен элементу ИЛИ по теореме ДеМоргана и двойному отрицанию.

Эта информация полезна при создании цифровой логики в лабораторных условиях, где логические элементы И-НЕ семейства TTL более доступны в самых разных конфигурациях, чем другие типы.

Процедура построения логики И-И-НЕ вместо логики И-ИЛИ следующая:

• Создание логической схемы сокращенной суммы продуктов.
• При построении схемы соединений СОП замените все вентили (И и ИЛИ) вентилями И-НЕ.
• Неиспользуемые входы должны быть связаны с высоким логическим уровнем.
• В случае устранения неполадок внутренние узлы на первом уровне выходов логического элемента И-НЕ НЕ соответствуют логическим уровням схемы И-ИЛИ, а инвертируются. Используйте логическую схему NAND-NAND. Однако входные данные и конечный результат идентичны.
• Обозначьте несколько пакетов U1, U2 и т. д.
• Используйте таблицу данных для присвоения номеров контактов входам и выходам всех ворот.

Пример:

Давайте вернемся к предыдущей проблеме, связанной с минимизацией СОП. Создайте решение на основе сумм. Сравните решение POS с предыдущей СОП.

Решение:

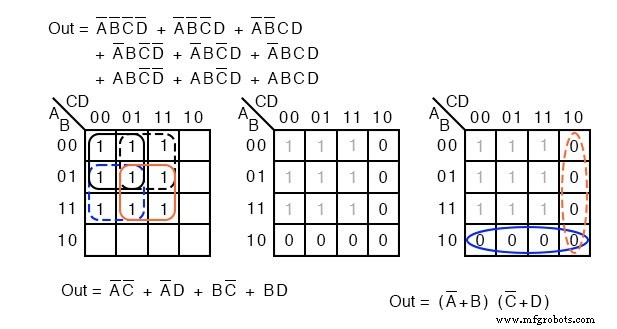
Вверху слева мы видим исходную задачу, начинающуюся с 9-минутного логического неупрощенного выражения. Проведя обзор, мы сформировали четыре группы по 4 ячейки, чтобы получить результат СОП с 4 продуктами, слева внизу.

На среднем рисунке выше мы заполняем пустые места подразумеваемым 0 с. 0 ы образуют две группы по 4 клетки. Сплошная синяя группа - (A ’+ B) . , красная пунктирная группа - (C ’+ D) . Это дает два суммовых члена в результате "произведение сумм", справа вверху Out =(A ’+ B) (C’ + D) .

Сравнение предыдущего упрощения SOP слева и упрощения POS справа показывает, что POS является наименее затратным решением. В СОП используется всего 5 ворот, в кассовом терминале - только 3 входа.

Это POS-решение даже при использовании TTL-логики выглядит привлекательно из-за простоты результата. Мы можем найти логические элементы И и ИЛИ с двумя входами.

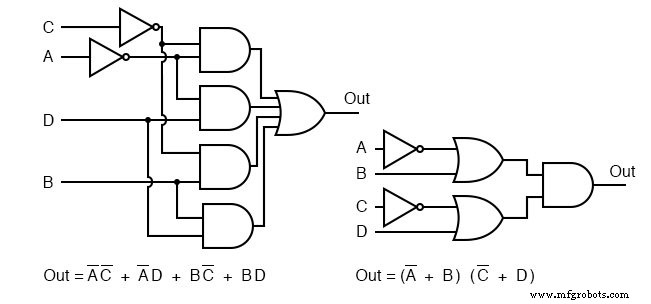
Диаграммы шлюзов SOP и POS показаны выше для нашей задачи сравнения.

С учетом выводов выводов затворов интегральных схем семейства логических TTL ниже, пометьте диаграмму maxterm вверху справа обозначениями цепей (U1-a, U1-b, U2-a и т. Д.) И номерами контактов.

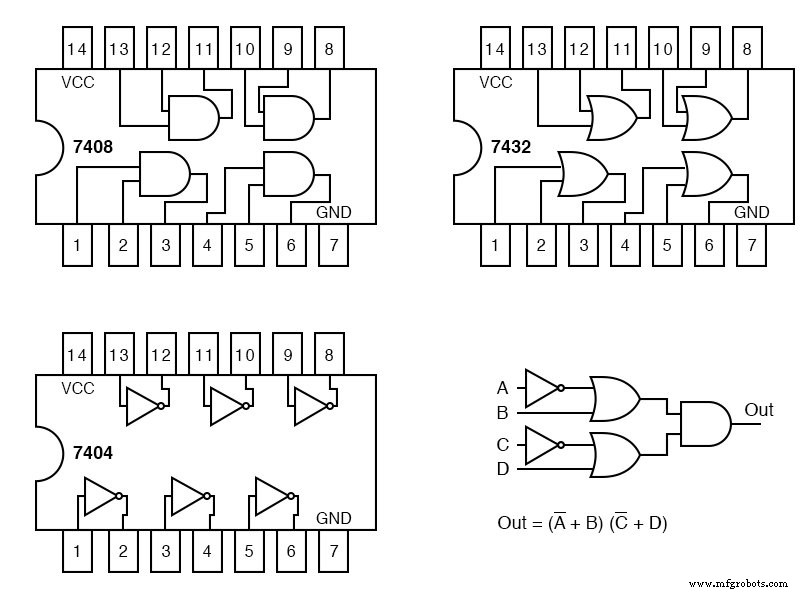
Каждый корпус интегральной схемы, который мы используем, получит обозначение схемы:U1, U2, U3. Чтобы различать отдельные ворота в пакете, они обозначаются буквами a, b, c, d и т. Д.

Шестнадцатеричный инверторный корпус 7404 - это U1. Отдельные инверторы в нем - это U1-a, U1-b, U1-c и т. Д. U2 назначается четырехъядерному логическому элементу ИЛИ 7432. U3 назначается квадрату 7408 и логическому элементу И.

Со ссылкой на номера выводов на диаграмме выше, мы назначаем номера выводов всем входам и выходам затвора на схеме ниже.

Теперь мы можем построить эту схему в лабораторных условиях. Или мы могли бы разработать печатную плату для этого. Печатная плата содержит «проводку» из медной фольги, поддерживаемую непроводящей подложкой из фенола или эпоксидного стекловолокна.

Печатные платы используются для массового производства электронных схем. Заземлите вводы неиспользуемых ворот.

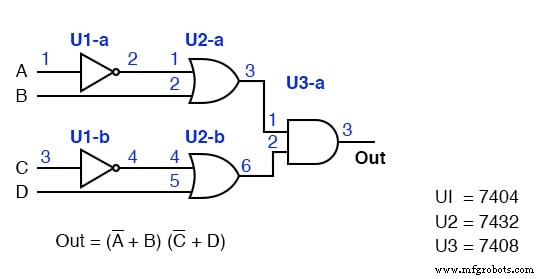
Пометьте предыдущую схему POS-решения вверху слева (третий рисунок сзади) обозначениями цепей и номерами контактов. Это будет похоже на то, что мы только что сделали.

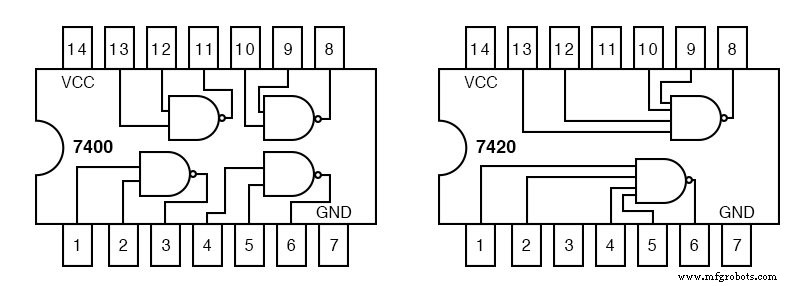
Мы можем найти 2-входные логические элементы И, 7408, в предыдущем примере. Однако у нас возникли проблемы с поиском логического элемента ИЛИ с 4 входами в нашем каталоге TTL.

Единственный тип логического элемента с 4 входами - вентиль NAND 7420, показанный наверху справа.

Мы можем превратить вентиль И-НЕ с 4 входами в вентиль ИЛИ с 4 входами, инвертировав входы в вентиль И-НЕ, как показано ниже. Таким образом, мы будем использовать логический элемент И-НЕ с 4 входами 7420 в качестве логического элемента ИЛИ, инвертируя входы.

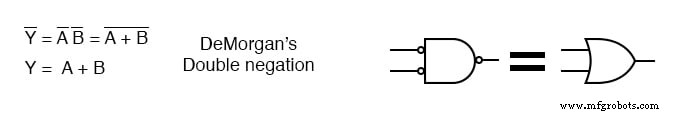
Мы не будем использовать дискретные инверторы для инвертирования входов 4-входного логического элемента NAND 7420, но будем управлять им с 2-входными вентилями NAND вместо логических элементов И, требуемых в решении SOP, minterm,

Инверсия на выходе логических элементов И-НЕ с 2 входами обеспечивает инверсию логических элементов ИЛИ с 4 входами.

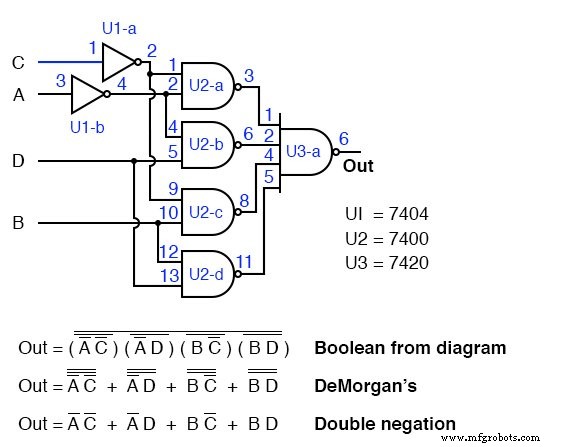
Результат показан выше. Это единственный практический способ создать его с помощью логических элементов TTL, используя логику NAND-NAND, заменяющую логику AND-OR.

СВЯЗАННЫЕ РАБОЧИЕ ТАБЛИЦЫ:

• Картографический лист Карно