Численная оптимизация геометрической конфигурации керамики в износостойких композитах HCCI / ZTAP на основе реальной модели частиц

Введение

С непрерывным развитием процесса индустриализации традиционные единичные износостойкие материалы постепенно становились трудными для удовлетворения требований к характеристикам износостойких деталей в областях металлургии, электроэнергетики и строительных материалов [1, 2]. Керамические частицы, армированные композитами с металлической матрицей, такие как матричные композиты из высокохромистого чугуна (HCCI), армированные керамическими частицами из закаленного оксида циркония (ZTA) (называемые HCCI / ZTA _P композиты в дальнейшем), являются одним из самых популярных износостойких материалов, который идеально сочетает в себе высокую твердость керамики ZTA с выдающейся ударной вязкостью HCCI и в полной мере использует взаимодополняющие отношения между ними, обеспечивая превосходную износостойкость металлической матрицы. композиты [3, 4].

HCCI / ZTA _P композиты все еще имеют некоторую тенденцию к растрескиванию, что может повлиять на внешний вид и стабильность продукции [5,6,7]. Растрескивание композиционных материалов связано с их пластичностью и напряженным состоянием. Превосходная пластичность и меньшее термическое напряжение могут снизить вероятность растрескивания композиционных материалов [8]. Если разница в коэффициенте теплового расширения между керамическими частицами и металлом слишком велика, термическое напряжение в композитах соответственно возрастет. Когда термическое напряжение велико, внутри композита могут возникать трещины, особенно на границе раздела между керамическими частицами и металлом. Непрерывное расширение и распространение трещин может со временем привести к разрушению композиционного материала или даже к отслаиванию всего слоя [9, 10]. HCCI / ZTA _P композитные материалы также имеют вышеуказанные проблемы. Когда расплавленный металл просачивается в агрегированные частицы, температура снижается, что приводит к плохой способности сочетать металл с керамическими частицами. Следовательно, для дальнейшего повышения производительности HCCI / ZTA _P композитов, важно изучить и уменьшить их склонность к растрескиванию [11, 12].

В HCCI / ZTA _P В композитах композитный слой выполнен в качестве рабочей поверхности, а остальная матрица - металлическая, что придает композиту одновременно высокую износостойкость и пластичность [13]. Составной слой готовится методом инфильтрации в HCCI / ZTA _P композитный. Одной из замечательных характеристик композиционных материалов является их конструктивность [14]. В соответствии с фактическим спросом из керамических частиц приготавливают преформу с особой структурой и размером, а затем преформу плотно смешивают с расплавленным металлом для получения ZTA _P / HCCI композит [15].

Чтобы снизить термическое напряжение, мы выбрали заготовку из керамических частиц в виде шестиугольника. В гексагональной заготовке максимальное расстояние, на которое расплавленный металл проникает в заготовку, одинаково независимо от направления, поэтому равномерность проникновения металла улучшается, а концентрация напряжений в заготовке снижается [16, 17]. Хотя гексагональная заготовка используется для уменьшения склонности материала к растрескиванию, термическое напряжение в процессе формования материала все еще существует. Улучшение структуры преформы керамических частиц может эффективно снизить концентрацию напряжений.

При оптимизации структуры композитной преформы метод конечных элементов может сократить количество повторных экспериментов. В предыдущих исследованиях из-за сложности вытяжки и расчета керамических частиц преформа керамических частиц обычно упрощалась в целом. Тщательное исследование показало, что упрощенная модель имеет некоторые недостатки и не может использоваться в более широком диапазоне. Создание модели эквивалентной частицы может дополнительно объединить модель с реальной ситуацией и уменьшить ошибку, вызванную моделью [18]. Программное обеспечение для анализа методом конечных элементов COMSOL Multiphysics используется для моделирования полей напряжений в процессе затвердевания и сжатия HCCI / ZTA _P композитный материал [19]. COMSOL Multiphysics - это программа для крупномасштабного современного численного моделирования [20, 21].

В статье мы используем программное обеспечение конечных элементов для моделирования напряжения композитных материалов в различных условиях. Версия COMSOL Multiphysics, используемая в этой статье, - 4.5a. В этом исследовании систематически анализируется влияние геометрической модели в программном обеспечении конечных элементов на результаты расчетов, что способствует проектированию и разработке пористого материала. Моделирование и эксперимент сравниваются друг с другом, и модель постоянно оптимизируется.

Методы

Одной из основных проблем при производстве композитов является концентрация напряжений, которая напрямую влияет на износостойкость и пластичность композитных материалов. Улучшение структуры преформы керамических частиц может эффективно снизить концентрацию напряжений. Целью данного исследования является изучение влияния структуры преформы на распределение напряжений и улучшение характеристик композитных материалов.

Создание и оптимизация геометрической модели

В процессе затвердевания температура формы и жидкого металла различается, и жидкий металл быстро затвердевает, поэтому теплопередача между каждым положением в процессе литья нестабильна, и уравнение теплопередачи может быть записано как [22]:

где \ (\ rho \) - плотность; \ (C _ {{\ text {P}}} \) - теплоемкости; \ (\ lambda \) - теплопроводность; Т переходная температура; Q тепло; координаты x , y , и z называются относительными координатами подсистемы.

Поскольку в процессе затвердевания температура в каждой точке разная, в отливке возникает переменное внутреннее напряжение. Если отливку можно рассматривать как тело с линейной упругостью, когда внутреннее напряжение меньше предела текучести, с процессом упругой деформации, мы можем использовать уравнение закона Гука для его описания.

где E - модуль Юнга; \ (\ sigma =\ sigma _ {{ii + \ sigma_ {11}}} + \ sigma_ {22 +} \ sigma_ {33} \); \ (v \) - коэффициент Пуассона; единичный тензор \ (\ varepsilon_ {ij} =\ frac {1} {2} \ gamma_ {ij} \); модуль сдвига \ (G =\ frac {E} {{2 \ left ({1 + v} \ right)}} \).

Тогда внутреннее напряжение превышает предел текучести, и отливка имеет большую деформацию. Полная деформация складывается из упругой деформации и пластической деформации \ (\ sigma_ {ij} =\ sigma_ {ij} ^ {e} + \ sigma_ {ij} ^ {p} \). Это уравнение можно рассматривать как модель упругопластического линейного упрочнения. Упругая деформация и пластическая деформация линейны, и определяющее уравнение можно записать в виде [23]:

где \ (\ sigma \) - деформация; E - модуль Юнга; \ (\ varepsilon \) - напряжение; \ (\ varepsilon _ {{\ text {s}}} \) - предел текучести.

Срок службы деталей из чугуна с высоким содержанием хрома короче из-за плохой износостойкости. Композиционные материалы имеют много преимуществ перед одиночным HCCI. В процессе производства HCCI / ZTA _P В композитах керамические частицы ZTA заранее приготавливаются в пористую заготовку. Заготовка обеспечивает более плотное соединение керамических частиц ZTA и HCCI, и керамические частицы непросто отвалиться при ударе. Для дальнейшего повышения производительности HCCI / ZTA _P композитов, необходимо оптимизировать структуру преформ.

В процессе литья расплавленный металл может заполнять круглые отверстия и увеличивать долю металла. В процессе подачи заявки HCCI / ZTA _P композитов, было обнаружено, что место скопления частиц более склонно к растрескиванию, поэтому в этом месте добавляется круглое отверстие.

Форма керамических частиц ZTA представляет собой произвольный многоугольник, и в преформе содержится много частиц. Если все частицы нарисованы, рабочая нагрузка большая. В предыдущих моделях композитов с металлической керамической матрицей большинство заготовок керамических частиц рассматривалось как единое целое. Как показано на рис. 1, в документе устанавливаются модели на макро- и микромасштабе, соответственно. Создание разумной модели требует многократной взаимной проверки экспериментами. В модели оптимизации результаты расчетов хорошо согласуются с результатами экспериментов. Результаты моделирования включали термическое напряжение, температурное поле, поле фазового перехода во время затвердевания и деформацию напряжения отливки под нагрузкой. Внесите разумные и эффективные корректировки в установленную модель конечных элементов, чтобы оптимизированную модель конечных элементов можно было использовать в более широком диапазоне.

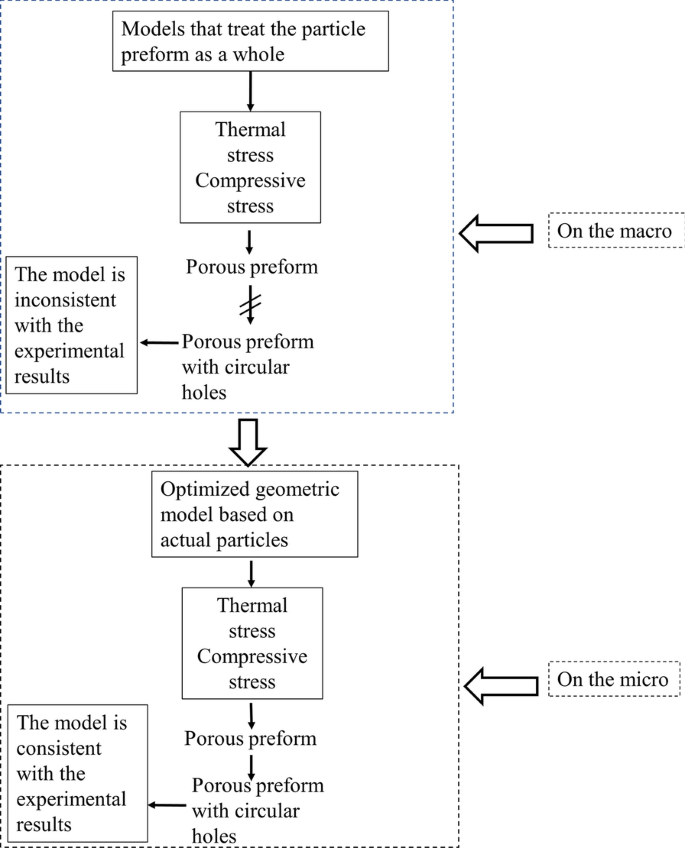
Блок-схема оптимизации геометрической модели для HCCI / ZTA _P материалы

При создании геометрической модели с использованием программного обеспечения конечных элементов, чтобы сократить время расчета и рабочую нагрузку моделирования, часто используется упрощенная геометрическая модель. Как показано на фиг. 2, между частицами есть зазоры, поскольку трехмерная гексагональная пористая заготовка упрощена до двухмерной модели, и для проецирования двухмерной модели выбран только один слой частиц. Таким образом, наложение частиц в трехмерном пространстве может эффективно избежать влияния на двухмерную геометрическую модель и разумно упростить модель и повысить эффективность вычислений.

Керамические частицы ZTA и геометрическая модель HCCI / ZTA _P композиты. а Пористый перформанс, b составная зона HCCI / ZTA _P композиты, c оптимизированная геометрическая модель на основе реальных частиц, d исходная геометрическая модель

В этой статье керамические частицы ZTA выбраны в качестве армирующей фазы композита. Керамические частицы ZTA представляют собой многофазную структурную керамику, полученную путем добавления диоксида циркония к оксиду алюминия и последующего спекания, при этом массовая доля оксида циркония составляет 18%, а массовая доля оксида алюминия составляет 82%. Чугун с высоким содержанием хрома представляет собой матрицу из композиционного материала, который содержит более 12% хрома и является отличным износостойким материалом.

Параметры материала имеют большое влияние на результат расчета методом конечных элементов. Параметры материала, необходимые для моделирования в этой статье, получены экспериментально и из литературы. Параметры материала керамических частиц ZTA и HCCI показаны в таблице 1.

Эксперименты

Для проверки пластичности и износостойкости HCCI / ZTA _P Композитный материал был проведен систематический тест для дальнейшего определения влияния структуры преформы. Универсальная испытательная машина SHT4305 использовалась для измерения характеристик сжатия HCCI / ZTA _P композиты. Размер образца для испытаний на сжатие составляет 10 × 10 × 25 мм, приложенная нагрузка - 30 тонн, скорость сжатия - 0,5 мм / мин.

Испытание на износостойкость HCCI / ZTA _P композит нужен. Превосходная стойкость к истиранию - важнейший критерий испытаний износостойких композитных материалов. HCCI / ZTA _P композиты в основном используются в переработке полезных ископаемых, производстве цемента и бумаги, и большая часть рабочих условий связана с трехкомпонентным абразивным износом. Чтобы смоделировать производительность службы HCCI / ZTA _P композитов в реальных условиях работы, насколько это возможно, протестировано HCCI / ZTA _P композитов на трехкомпонентном абразивном измерителе износа ММН-5. Материал дорожки тестера - инструментальная сталь М2, твердость 820–860 Hv, наружный диаметр 380 мм, ширина 20 мм. Тип и размер абразивов подбираются в зависимости от условий работы. В данной статье для абразивов используется кварцевый песок, твердость 1000–1200 Hv, испытательная нагрузка 40 Н, скорость вращения образца 30 об / мин.

Наноиндентор используется для выполнения теста модуля Юнга по 100 точкам в выбранных 100 × 100 мкм ² микрорайон. Модель наноиндентора - iMicro.

Износостойкость материалов можно измерить по уменьшению массы, уменьшению объема и так далее. Потеря объема, измеренная измерительным цилиндром с небольшими изменениями, может легко вызвать ошибки в показаниях человека. Следовательно, при одинаковых условиях износа потеря массы Δm используется для оценки характеристик износостойкости материала. Формула для расчета материальных потерь выглядит следующим образом:

где м ₁ и м ₂ , соответственно, представляют собой массу образцов до и после износа.

Результаты и обсуждение

Моделирование на основе упрощенной всей модели

При моделировании термического напряжения в процессе затвердевания HCCI / ZTA _P Для композитов в данном исследовании для всех результатов моделирования выбрано распределение теплового напряжения за 10 с, поскольку термическое напряжение значительно изменяется до и после 10 с. По сравнению со шкалой справа на рис. 3 красный цвет указывает на более высокое напряжение, а синий цвет указывает на более низкое напряжение. На рис. 3а концентрация напряжений появилась на краю заготовки, особенно в среднем положении, верхняя и нижняя стороны заготовки выглядели красными. Сравнивая с правой шкалой рис. 3а, видно, что напряжение здесь огромно. Синий цвет появляется в том месте, где собираются частицы, то есть на пересечении стенок шестиугольного отверстия, указывая на то, что здесь напряжение невелико. В геометрической модели на рис. 3c круглые отверстия добавляются к агрегатам частиц преформы. Распределение напряжений на рис. 3c похоже на рис. 3a, за исключением того, что существует более очевидная концентрация напряжений вокруг круглых отверстий. Распределение напряжений вокруг круглого отверстия перфорации на рис. 4 аналогично изображению на рис. 3

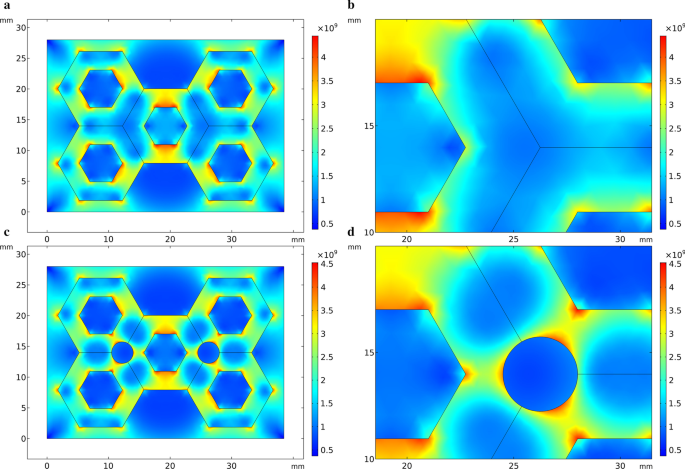
Распределение термических напряжений при затвердевании в упрощенной модели. а Начальное выступление, б частичное увеличенное изображение первоначального выступления, б преформа с добавленными круглыми отверстиями, d частично увеличенный вид выступления с добавленными круглыми отверстиями

Напряжение сжатия в упрощенной модели. а Начальное выступление, б частичное увеличенное изображение первоначального выступления, б преформа с добавленными круглыми отверстиями, d частично увеличенный вид выступления с добавленными круглыми отверстиями

Окончательные результаты расчетов должны быть интуитивно понятными, поэтому результаты были обработаны после обработки и была составлена ​​сравнительная таблица поперечных напряжений. Сначала нарисуйте двумерное поперечное сечение в геометрической модели, потому что основная часть наблюдения находится вокруг круглого отверстия, то есть там, где собираются частицы, поэтому двумерное поперечное сечение проходит через круглое отверстие. Ордината графика напряжений - это значение напряжения на линии сечения, а абсцисса - это x . -осевая координата модели, как показано на рис. 5. В упрощенной модели круговые координаты отверстия равны (12, 14), (27, 14). Рисунок 5c представляет собой линейный график напряжения затвердевания. На фиг. 5с преформа с круглыми отверстиями имеет значительное увеличение напряжения на абсциссах 12 и 27 по сравнению с преформой без круглых отверстий. Рисунок 5d представляет собой сравнительную диаграмму напряжения сжатия. Общая тенденция кривой такая же, как на рис. 5c, и напряжение расположения круглого отверстия значительно возрастет.

Положение 2D поперечного сечения упрощенной модели и сравнение поперечного напряжения. а Начальное выступление, б частичное увеличенное изображение первоначального выступления, c преформа с добавленными круглыми отверстиями, d частично увеличенный вид выступления с добавленными круглыми отверстиями

Моделирование на основе эквивалентной модели зерна

На рисунке 6 показано распределение термического напряжения HCCI / ZTA _P . модель композитов, основанная на реальных частицах, которая аналогична рис. 3. Однако на рис. 6 керамические частицы ZTA больше не упрощены как целая преформа, а представлены как отдельные частицы, и можно заметить, что большая часть частицы вокруг приобретают красный цвет. Форма керамических частиц ZTA неоднородна, а напряжение превышает окружающее значение, особенно на острие частиц. Распределения термических напряжений на рис. 3b и 6b, очевидно, разные. Круглое отверстие в заготовке на рис. 6b имеет синий цвет, что указывает на то, что напряжение здесь невелико. Результаты расчета концентрации напряжений вокруг круглого отверстия противоположны. Степень упрощения и способы рисования геометрических моделей приводят к разным результатам расчетов.

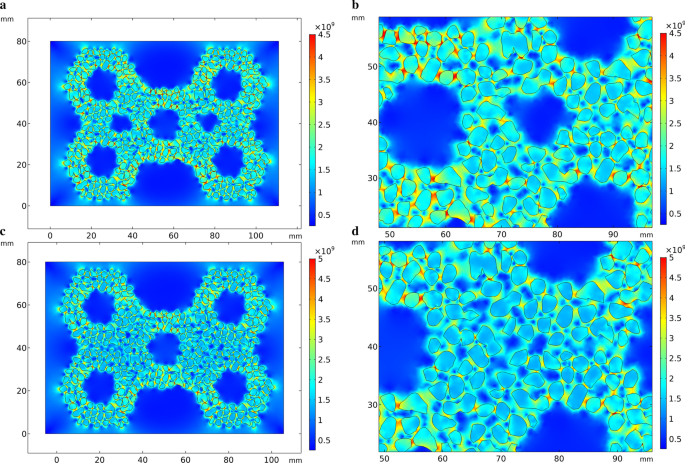
Распределение термических напряжений при затвердевании в оптимизированной модели. а Начальное выступление, б частичное увеличенное изображение первоначального выступления, c преформа с добавленными круглыми отверстиями, d частично увеличенный вид выступления с добавленными круглыми отверстиями

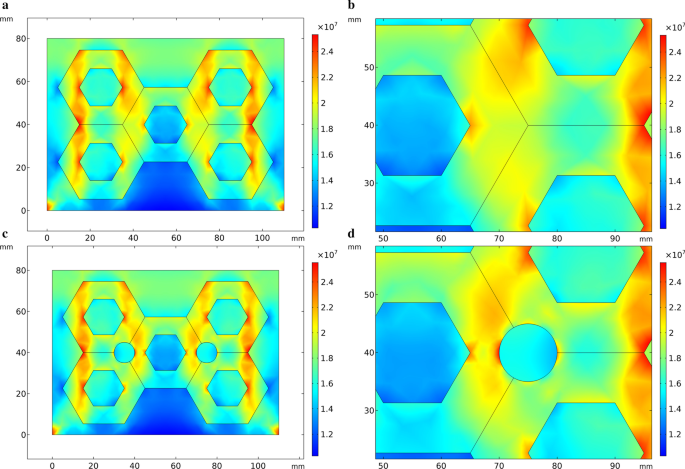
Геометрическая модель, используемая для моделирования сжимающего напряжения на рис. 7, аналогична рис. 6. На рис. 7, по сравнению с масштабом справа, напряжение сосредоточено в верхней части модели и преформы, особенно края керамической преформы с обеих сторон желто-зеленого цвета. В части агрегации частиц преформы эта зона показана зеленым цветом на рис. 7а, что указывает на то, что здесь напряжение невелико. На рис. 7b круглые отверстия добавлены к агрегатам преформы. Цвет зоны круглых отверстий зеленый и желтый, что указывает на отсутствие явной концентрации напряжений.

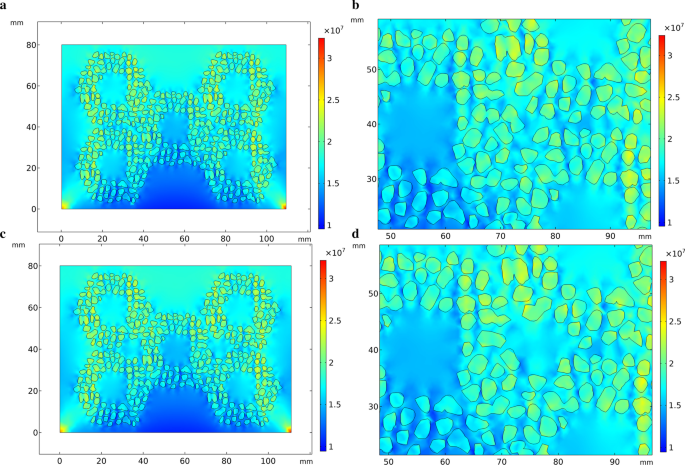
Напряжение сжатия в оптимизированной модели. а Начальное выступление, б частичный увеличенный вид оптимизированной производительности, c преформа с добавленными круглыми отверстиями, d частично увеличенный вид выступления с добавленными круглыми отверстиями

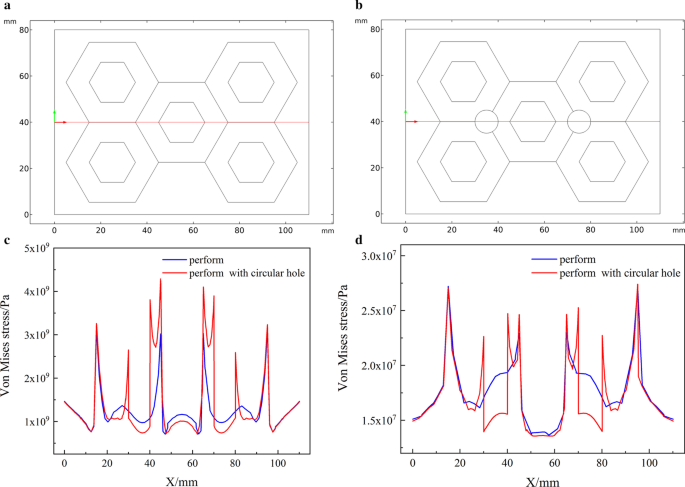
В модели, основанной на реальных частицах, координаты круглого отверстия равны (12, 14) (27, 14). На рисунке 8 представлена ​​сравнительная диаграмма напряжения затвердевания, в которой сравнивается влияние наличия или отсутствия круглых отверстий на напряжение. Напряжение преформы с круглыми отверстиями значительно уменьшилось на абсциссах 12 и 27, и его положение в основном совпало с положением круглых отверстий. Напряжение остальных координат заготовки с круглыми отверстиями немного увеличилось. На рис. 8a, b две кривые в основном совпадают, за исключением заготовки с круглыми отверстиями; напряжение около круглых координат отверстия значительно снижается.

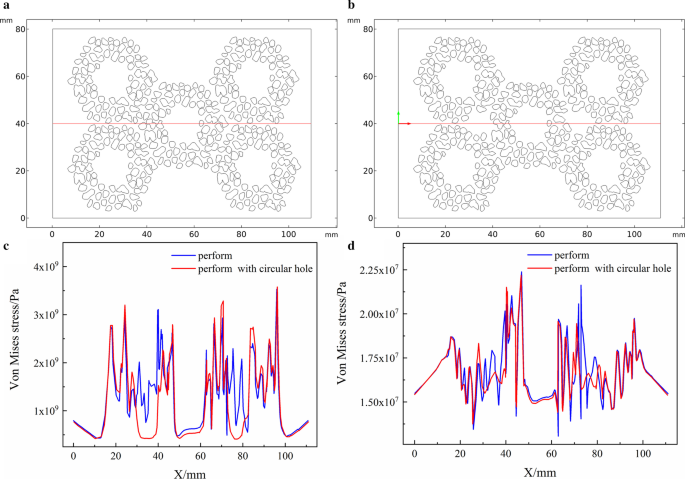
Положение 2D-поперечного сечения оптимизированной модели и сравнение поперечного напряжения. а Начальное выступление, б преформа с добавленными круглыми отверстиями, c напряжение затвердевания, d напряжение сжатия

Экспериментальные проверки

Из рис.9 видно, что при испытании на износ потеря массы композитов с использованием оптимизированной преформы и композитов с исходной преформой не сильно различается, что указывает на то, что износостойкость существенно не ухудшается и может также улучшить общая пластичность HCCI / ZTA _P композиты.

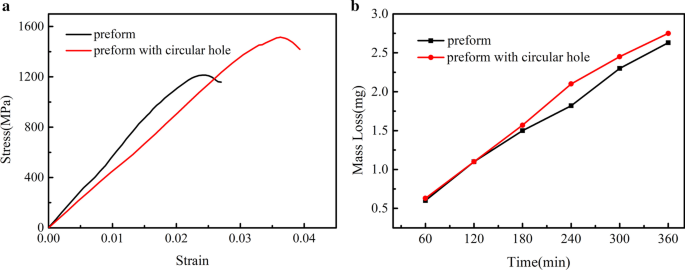
Кривая напряжения сжатия при сжатии HCCI / ZTA _P композитный материал и потеря массы трехкомпонентного абразива на стыке композитных сотовых стен

Пористая преформа была оптимизирована путем добавления цилиндрических отверстий небольшого размера в зонах агрегации частиц, что изменило объемную долю керамических частиц в HCCI / ZTA _P композиты. Содержание керамических частиц ZTA в композиционном материале является важным фактором, влияющим на его механические свойства. Как показано на рис.9, прочность на сжатие и деформация сжатия образца, который имеет преформы с круглыми отверстиями, значительно увеличиваются по сравнению с образцом с исходной преформой, что указывает на то, что небольшие круглые отверстия в зонах агрегации керамических частиц ZTA способствуют улучшению прочность и пластичность HCCI / ZTA _P композиты. Добавление небольших цилиндрических отверстий в зонах агломерации пористой преформы увеличит содержание металлической матрицы, тем самым увеличивая деформацию сжатия HCCI / ZTA _P композиты, подверженные сжимающему напряжению, а также влияющие на его прочность на сжатие. Когда напряжение достигает пикового значения, можно считать, что в образце уже произошло повреждение. При постоянном увеличении деформации внутреннее повреждение материала также накапливается, сопротивление деформации постепенно уменьшается и, наконец, происходит разрушение при сдвиге.

Результаты микроанализа твердости всех образцов показаны на фиг. 10. Как показано на фиг. 10a, b, испытательная зона выбирается вокруг закругленных частиц и частиц с острыми углами соответственно, чтобы лучше соответствовать результатам моделирования. Рисунок 10c, d сравнивается с увеличенным частичным изображением напряжения. При моделировании концентрация напряжений имеет тенденцию происходить вокруг острых углов частиц. По результатам испытаний модуль упругости около частиц с острыми углами больше, чем у металлической матрицы около закругленных углов, что дополнительно подтверждает рациональность модели на основе реальной частицы.

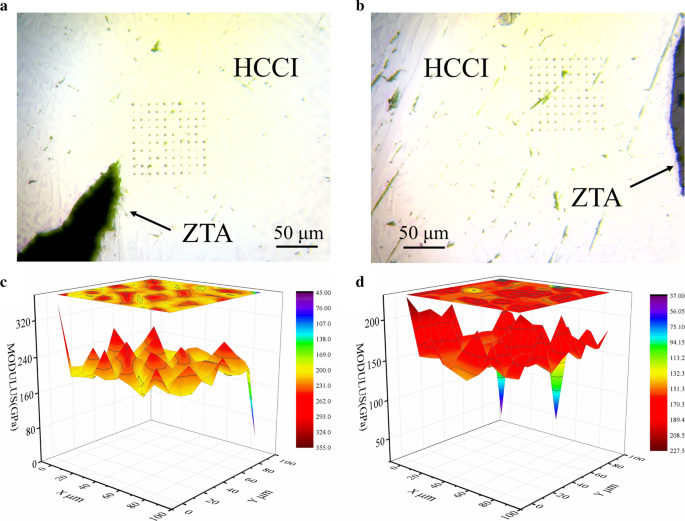
Распределение вдавливания композиционных материалов и распределение модуля Юнга вокруг частиц композиционных материалов. а Форма частиц резкая, b форма частиц округлая, c форма частиц резкая, d форма частиц округлая

К зонам агрегации частиц преформ добавлено круглое отверстие, которое выполняет три функции. Первая функция - уменьшить объемную долю керамических частиц в HCCI / ZTA _P композитный материал и снизить остаточные напряжения; вторая функция - уменьшить агломерацию керамических частиц преформы; третья функция - увеличить объемную долю металлической матрицы с лучшей пластичностью, чтобы препятствовать распространению трещин. Пластичность HCCI / ZTA _P композитов уменьшается с увеличением остаточного напряжения. Объемная доля керамических частиц уменьшается, а остаточное напряжение становится относительно небольшим. Добавление круглых отверстий в заготовку из керамических частиц ZTA может уменьшить трещины, потому что неустойчивость трещин имеет тенденцию распространяться по прямой линии. При образовании трещин в композитной зоне HCCI / ZTA _P Композитный материал, трещины легко расширяются вдоль стенки шестиугольного отверстия в преформе, вызывая распространение трещины. Круглое отверстие увеличивает содержание HCCI-матрицы на стыке стенки шестиугольного отверстия, препятствует распространению трещин и, таким образом, играет роль в повышении прочности конструкции.

Заключение

Большая разница в коэффициенте теплового расширения между HCCI и ZTA _P вызывает трещины в композитном материале. Процесс затвердевания и сжатия HCCI / ZTA _P композитные материалы моделируются с использованием программного обеспечения конечных элементов, а численные значения и распределения напряжений анализируются на основе упрощенной полной модели и эквивалентной модели зерна для преформы. По результатам расчета оптимизирована конструкция преформы. Анализируя результаты моделирования и экспериментов, можно сделать вывод, что добавление круглых отверстий в гексагональную пористую заготовку приведет к снижению термического напряжения и сжимающего напряжения во время затвердевания. После оптимизации и настройки модели результаты моделирования, как правило, согласуются с экспериментальными результатами. Методы, описанные в этой статье, могут служить важным справочным материалом для моделирования и оптимизации параметров обработки в системах литья из различных композиционных материалов с металлической матрицей.

Доступность данных и материалов

Наборы данных, подтверждающие выводы этой статьи, включены в статью.

Сокращения

HCCI:

Чугун с высоким содержанием хрома

ZTA:

Оксид алюминия, закаленный диоксидом циркония

HCCI / ZTA _P :

Композиты с матрицей из чугуна с высоким содержанием хрома, армированные композитами с керамическими частицами на основе оксида алюминия, упрочненного диоксидом циркония