Принципы проектирования надежности для инженера-технолога

Все чаще менеджеры и инженеры, отвечающие за производство и другие производственные процессы, уделяют повышенное внимание надежности своим стратегическим и тактическим планам и инициативам. Эта тенденция затрагивает многие функциональные области, включая проектирование и закупку машин / систем, эксплуатацию и техническое обслуживание оборудования.

Проектирование надежности как дисциплина, зародившаяся в авиационной промышленности, исторически ориентировалось в первую очередь на обеспечение надежности продукции. Все чаще и чаще эти методы используются для обеспечения надежности производства на производственных предприятиях и оборудовании - часто в качестве средства бережливого производства. Эта статья представляет собой введение в наиболее актуальные и практичные из этих методов проектирования надежности станции, в том числе:

• Основные расчеты надежности для частоты отказов, наработки на отказ, доступности и т. д.
• Введение в экспоненциальное распределение - краеугольный камень методов надежности.
• Определение зависимостей времени отказа с помощью универсальной системы Weibull.
• Разработка эффективной системы сбора полевых данных.

История проектирования надежности

Истоки инженерии надежности, по крайней мере, спрос на нее, можно проследить до того момента, когда человек начал полагаться на машины как на средства к существованию. Например, Noria - это древний насос, который считается первой сложной машиной в мире. Используя гидравлическую энергию потока реки или ручья, Noria использовала ковши для перекачки воды в желоба, виадуки и другие распределительные устройства для орошения полей и обеспечения водой местных сообществ.

Если община Нория потерпит неудачу, люди, которые зависели от нее в плане снабжения едой, оказались в опасности. Выживание всегда было отличным источником мотивации для надежности и надежности.

Хотя истоки ее спроса древние, инженерия надежности как техническая дисциплина по-настоящему процветала вместе с ростом коммерческой авиации после Второй мировой войны. Для руководителей компаний авиационной отрасли быстро стало очевидно, что аварии вредны для бизнеса. Карен Берновски, редактор журнала Quality Progress , раскрыла в одной из своих передовых статей исследования ценности смерти различными способами для СМИ, которое было проведено профессором статистики Массачусетского технологического института Арнольдом Барнеттом и опубликовано в 1994 году.

Барнетт оценил количество новостных статей на первой полосе New York Times на 1000 смертей различными способами. Он обнаружил, что связанные с раком смерти дают 0,02 новостных статьи на первой полосе на 1000 смертей, убийства - 1,7 на 1000 смертей, СПИД - 2,3 на 1000 смертей, а авиационные происшествия - 138,2 статьи на 1000 смертей!

Стоимость и значительный характер авиационных происшествий помогли авиационной отрасли активно участвовать в развитии инженерной дисциплины по обеспечению надежности. Точно так же, из-за критического характера военной техники в обороне, методы обеспечения надежности уже давно используются для обеспечения оперативной готовности. Многие из наших стандартов в области проектирования надежности являются стандартами MIL или берут свое начало в военной деятельности.

Что такое проектирование надежности?

Инжиниринг надежности имеет дело с долговечностью и надежностью деталей, продуктов и систем. Более того, речь идет об управлении риском. Инжиниринг надежности включает в себя широкий спектр аналитических методов, призванных помочь инженерам понять виды отказов и характер отказов этих деталей, продуктов и систем. Традиционно в области проектирования надежности основное внимание уделялось обеспечению надежности и надежности продукции.

В последние годы организации, развертывающие машины и другие физические активы в производственных условиях, начали внедрять различные принципы проектирования надежности с целью обеспечения производственной надежности и надежности.

Производственные организации все чаще применяют методы проектирования надежности, такие как обслуживание, ориентированное на надежность (RCM), включая анализ видов отказов и последствий (и критичности) (FMEA, FMECA), анализ первопричин (RCA), техническое обслуживание на основе состояния, улучшенные схемы планирования работы, Эти же организации начинают применять стратегии проектирования и закупок, основанные на стоимости жизненного цикла, схемы управления изменениями и другие передовые инструменты и методы, чтобы контролировать основные причины низкой надежности.

Однако принятие более количественных аспектов проектирования надежности сообществом по обеспечению производственной надежности было медленным. Частично это связано с кажущейся сложностью методов, а частично - с трудностью получения полезных данных.

Количественные аспекты проектирования надежности могут на первый взгляд показаться сложными и устрашающими. В действительности, однако, относительно базовое понимание наиболее фундаментальных и широко применимых методов может позволить инженеру по надежности предприятия получить гораздо более четкое представление о том, где возникают проблемы, их природе и их влиянии на производственный процесс - по крайней мере, в количественном отношении. смысл.

При правильном использовании инструменты и методы количественного проектирования надежности позволяют инжинирингу надежности предприятия более эффективно применять структуры, предоставляемые RCM, RCA и т. Д., За счет устранения некоторых догадок, связанных с их применением в противном случае. Однако инженеры должны быть особенно умными в применении этих методов.

Почему? Операционный контекст и среда производственного процесса включают в себя больше переменных, чем несколько одномерный мир обеспечения надежности продукта. Это связано с совокупным влиянием проектирования, закупок, производства / эксплуатации, технического обслуживания и т. Д., А также со сложностью создания эффективных тестов и экспериментов для моделирования многомерных аспектов типичной производственной среды.

Несмотря на возросшую сложность применения методов количественной надежности в производственной среде, тем не менее, стоит получить хорошее представление об инструментах и ​​применять их там, где это необходимо. Количественные данные помогают определить характер и масштаб проблемы / возможности, что дает представление о надежности его или ее применения других инструментов проектирования надежности.

Эта статья предоставит введение в самые основные методы проектирования надежности, которые применимы к производственному инженеру, который заинтересован в обеспечении надежности производства. Он предполагает базовое понимание алгебры, теории вероятностей и одномерной статистики, основанной на гауссовском (нормальном) распределении (например, мера центральной тенденции, меры дисперсии и изменчивости, доверительные интервалы и т. Д.).

Следует пояснить, что эта статья представляет собой краткое введение в методы обеспечения надежности. Это ни в коем случае не исчерпывающий обзор методов проектирования надежности, и он не является каким-либо новым или нетрадиционным. Описанные здесь методы обычно используются инженерами по надежности и являются основными концепциями знаний для тех, кто проходит профессиональную сертификацию Американского общества качества (ASQ) в качестве инженера по надежности (CRE).

Несколько книг по проектированию надежности перечислены в библиографии этой статьи. Автор этой статьи нашел методы обеспечения надежности для инженеров К.С. Кришнамурти и Статистика надежности Роберта Довича, чтобы быть особенно полезными и удобными для пользователя справочными материалами по методам проектирования надежности. Оба издаются ASQ Press.

Прежде чем обсуждать методы, вам следует ознакомиться с номенклатурой инженерной надежности. Для удобства в приложении к этой статье приводится сильно сокращенный список ключевых терминов и определений. Для более полного определения терминов и номенклатуры надежности обратитесь к MIL-STD-721 и другим связанным стандартам. Определения, содержащиеся в приложении, взяты из стандарта MIL-STD-721.

Основные математические концепции в проектировании надежности

Многие математические концепции применимы к проектированию надежности, особенно в областях вероятности и статистики. Аналогичным образом, многие математические распределения могут использоваться для различных целей, включая гауссово (нормальное) распределение, логнормальное распределение, распределение Рэлея, экспоненциальное распределение, распределение Вейбулла и множество других.

В целях этого краткого введения мы ограничимся обсуждением экспоненциального распределения и распределения Вейбулла, которые наиболее широко применяются в проектировании надежности. В интересах краткости и простоты были исключены важные математические концепции, такие как соответствие распределения и доверительные интервалы.

Частота отказов и среднее время наработки на отказ / до отказа (MTBF / MTTF)

Целью количественных измерений надежности является определение скорости отказов относительно времени и моделирование этой интенсивности отказов в математическом распределении с целью понимания количественных аспектов отказа. Самым основным строительным блоком является частота отказов, которая оценивается с помощью следующего уравнения:

Где:
λ =частота отказов (иногда называемая степенью опасности)
T =Общее время пробега / циклов / миль / и т. Д. в течение периода расследования как неудавшихся, так и исправных элементов.
r =Общее количество сбоев, произошедших в течение периода расследования.

Например, если пять электродвигателей работают вместе в течение 50 лет с пятью функциональными отказами в течение периода, интенсивность отказов составляет 0,1 отказа в год.

Еще одна очень базовая концепция - это среднее время наработки на отказ / наработка на отказ (MTBF / MTTF). Единственная разница между MTBF и MTTF заключается в том, что мы используем MTBF, когда ссылаемся на элементы, которые ремонтируются при выходе из строя. Для элементов, которые просто выбрасываются и заменяются, мы используем термин MTTF. Вычисления такие же.

Базовый расчет для оценки средней наработки на отказ (MTBF) и средней наработки на отказ (MTTF), оба показателя центральной тенденции, просто обратен функции частоты отказов. Он рассчитывается по следующему уравнению.

Где:
θ =Среднее время между отказом и отказом
T =Общее время пробега / циклов / миль / и т. Д. в течение периода расследования как неудавшихся, так и исправных элементов.
r =Общее количество сбоев, произошедших в течение периода расследования.

Среднее время безотказной работы для нашего примера промышленного электродвигателя составляет 10 лет, что является обратной величиной частоты отказов электродвигателей. Кстати, мы бы оценили наработку на отказ для электродвигателей, которые восстанавливаются после отказа. Для двигателей меньшего размера, которые считаются одноразовыми, мы определяем меру центральной тенденции как MTTF.

Интенсивность отказов является основным компонентом многих более сложных расчетов надежности. В зависимости от механической / электрической конструкции, условий эксплуатации, окружающей среды и / или эффективности обслуживания частота отказов машины как функция времени может снижаться, оставаться постоянной, линейно или геометрически возрастать (рис. 1). Важность соотношения количества отказов и времени будет обсуждаться более подробно позже.

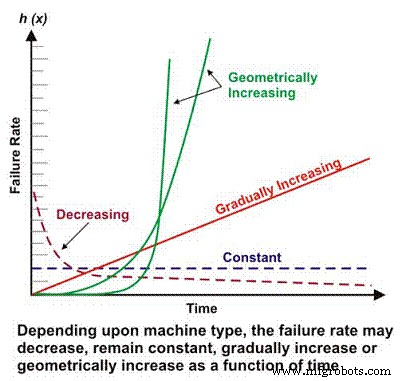
Рис. 1. Различная частота отказов в зависимости от времени

Кривая «ванна»

Люди, прошедшие только базовую подготовку в области вероятности и статистики, вероятно, наиболее знакомы с гауссовым или нормальным распределением, которое связано со знакомой колоколообразной кривой плотности вероятности. Распределение Гаусса обычно применимо к наборам данных, в которых два наиболее распространенных показателя центральной тенденции, среднее и медианное, примерно равны.

Удивительно, но, несмотря на универсальность распределения Гаусса при моделировании вероятностей явления, варьирующегося от результатов стандартизированных тестов до веса новорожденных при рождении, это распределение не является доминирующим распределением, используемым в проектировании надежности. Распределение Гаусса имеет свое место при оценке характеристик отказов машин с преобладающим режимом отказа, но основным распределением, используемым в проектировании надежности, является экспоненциальное распределение.

При оценке характеристик надежности и отказов машины мы должны начать с сильно искаженной кривой «ванны», которая отражает интенсивность отказов в зависимости от времени (рис. 2). Концептуально кривая ванны эффективно демонстрирует три основных характеристики интенсивности отказов машины:снижение, постоянство или увеличение. К сожалению, кривая ванны подверглась резкой критике в технической литературе по техническому обслуживанию, поскольку она не может эффективно моделировать характерную интенсивность отказов для большинства машин на промышленном предприятии, что обычно верно на макроуровне.

Большинство машин проводят свою жизнь в раннем возрасте или в младенческой смертности и / или в областях с постоянной интенсивностью отказов кривой ванны. Мы редко видим системные отказы в промышленных машинах, зависящие от времени. Несмотря на свои ограничения в моделировании интенсивности отказов типичных промышленных машин, кривая ванны является полезным инструментом для объяснения основных концепций проектирования надежности.

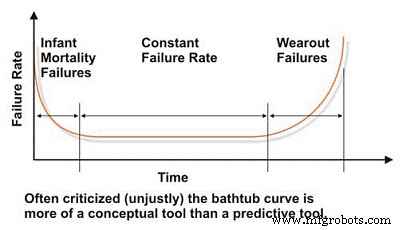
Рис. 2. Оскорбляемая кривая "ванна"

Человеческое тело - отличный пример системы, которая следует изгибу ванны. Люди и другие органические виды в этом отношении, как правило, страдают от высокого процента неудач (смертности) в течение первых лет жизни, особенно в первые несколько лет, но этот показатель снижается по мере взросления ребенка. Если предположить, что человек достигает половой зрелости и доживает до подросткового возраста, его или ее уровень смертности становится довольно постоянным и остается на этом уровне до тех пор, пока возрастные (временные) болезни не начнут повышать уровень смертности (износ).

На показатели смертности влияют многочисленные факторы, включая дородовой уход и питание матери, качество и доступность медицинской помощи, окружающую среду и питание, выбор образа жизни и, конечно же, генетическую предрасположенность. Эти факторы можно образно сравнить с факторами, влияющими на срок службы машины. Дизайн и снабжение аналогичны генетической предрасположенности; установка и ввод в эксплуатацию аналогичны дородовой помощи и питанию матери; выбор образа жизни и доступность медицинского обслуживания аналогичны эффективности технического обслуживания и упреждающему контролю за условиями эксплуатации.

Экспоненциальное распределение

Экспоненциальное распределение, самая основная и широко используемая формула прогнозирования надежности, моделирует машины с постоянной интенсивностью отказов или плоской частью кривой ванны. Большинство промышленных машин проводят большую часть своей жизни с постоянной интенсивностью отказов, поэтому это широко применимо. Ниже приведено основное уравнение для оценки надежности машины, которое следует экспоненциальному распределению, где частота отказов постоянна как функция времени.

Где:
R (t) =оценка надежности за период времени, циклы, мили и т. Д. (T).
e =Основание натурального логарифма (2,718281828)
λ =Частота отказов (1 / MTBF или 1 / MTTF)

В нашем примере с электродвигателем, если вы предположите постоянную интенсивность отказов, вероятность работы двигателя в течение шести лет без сбоев или прогнозируемая надежность составляет 55 процентов. Это рассчитывается следующим образом:
R (6) =2,718281828- (0,1 * 6)
R (6) =0,5488 =~ 55%

Другими словами, через шесть лет примерно 45% идентичных двигателей, работающих в идентичном приложении, с большой вероятностью выйдут из строя. Здесь стоит повторить, что эти расчеты прогнозируют вероятность для популяции. Любой конкретный человек из популяции может выйти из строя в первый день операции, в то время как другой человек может прослужить 30 лет. Такова природа вероятностных прогнозов надежности.

Характерной чертой экспоненциального распределения является то, что среднее время безотказной работы возникает в точке, в которой расчетная надежность составляет 36,78%, или в точке, в которой 63,22% машин уже вышли из строя. В нашем примере с двигателем через 10 лет можно ожидать, что 63,22% двигателей из совокупности идентичных двигателей, работающих в идентичных приложениях, выйдут из строя. Другими словами, выживаемость составляет 36,78% населения.

Мы часто говорим о прогнозируемом сроке службы подшипников как о сроке службы L10. Это момент времени, когда можно ожидать выхода из строя 10% группы подшипников (выживаемость 90%). На самом деле только часть подшипников доживает до точки L10. Мы пришли к выводу, что это объективный срок службы подшипника, хотя, возможно, нам следует нацелиться на точку L63.22, что указывает на то, что наши подшипники в среднем работают до прогнозируемого среднего времени безотказной работы - конечно, при условии, что подшипники следуйте экспоненциальному распределению. Мы обсудим этот вопрос позже в разделе статьи, посвященном анализу Вейбулла.

Функция плотности вероятности (pdf) или распределение срока службы - это математическое уравнение, которое аппроксимирует распределение частоты отказов. Это pdf, или распределение частот жизни, которое дает знакомую колоколообразную кривую в гауссовом, или нормальном, распределении. Ниже представлен файл в формате PDF для экспоненциального распределения.

Где:
pdf (t) =Распределение частот жизни за заданное время (t)
e =Основание натурального логарифма (2,718281828)
λ =Частота отказов (1 / MTBF или 1 / MTTF)

В нашем примере с электродвигателем фактическая вероятность отказа через три года рассчитывается следующим образом:
pdf (3) =01. * 2,718281828- (0,1 * 3)
pdf (3) =0,1 * 0,7408
pdf (3) =0,07408 =~ 7,4%

В нашем примере, если мы предположим постоянную интенсивность отказов, которая следует экспоненциальному распределению, распределение срока службы или pdf для промышленных электродвигателей будет выражено на рисунке 3. Пусть вас не смущает убывающий характер функции pdf. Да, частота отказов постоянна, но PDF-файл математически предполагает отказ без замены, поэтому совокупность, из-за которой могут возникать отказы, постоянно сокращается - асимптотически приближаясь к нулю.

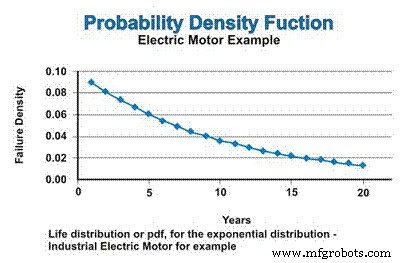
Рис. 3. Функция плотности вероятности (pdf)

Кумулятивная функция распределения (cdf) - это просто кумулятивное количество отказов, которое можно ожидать за определенный период времени. Для экспоненциального распределения частота отказов постоянна, поэтому относительная частота, с которой отказавшие компоненты добавляются в cdf, остается постоянной. Однако по мере того, как популяция сокращается в результате отказа, фактическое количество математически оцененных отказов уменьшается в зависимости от сокращающейся совокупности. Подобно тому, как PDF асимптотически приближается к нулю, PDF асимптотически приближается к единице (рисунок 4).

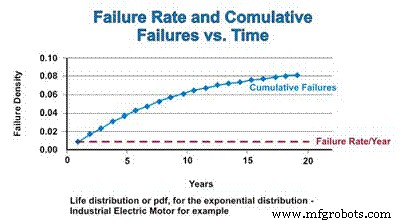
Рис. 4. Частота отказов и функция кумулятивного распределения

Часть кривой с уменьшающейся частотой отказов, которую часто называют областью младенческой смертности, и область износа будут обсуждаться в следующем разделе, посвященном универсальному распределению Вейбулла.

Распределение Weibull

Изначально разработанный шведским математиком Валлоди Вейбуллом, анализ Вейбулла является наиболее универсальным распределением, используемым инженерами по надежности. Хотя это называется распределением, на самом деле это инструмент, который позволяет инженеру по надежности сначала охарактеризовать функцию плотности вероятности (распределение частоты отказов) набора данных отказов, чтобы охарактеризовать отказы как ранний срок службы, постоянный (экспоненциальный) или износ (Гауссовский или логарифмический нормальный) путем нанесения данных о времени до отказа на специальной бумаге для построения графиков с записью журнала времени / циклов / миль до отказа на оси X в масштабе журнала в сравнении с кумулятивным процентом генеральной совокупности, представленной каждым отказом в журнале. -log масштабированная ось Y (рисунок 5).

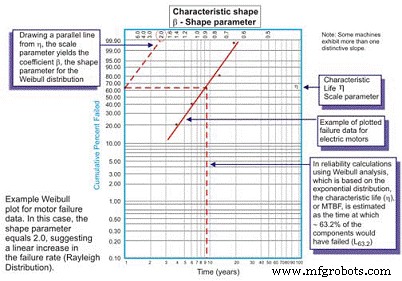
Рис. 5. Простой график Вейбулла - с комментариями

После построения линейный наклон результирующей кривой является важной переменной, называемой параметром формы, представленной символом â, который используется для корректировки экспоненциального распределения для соответствия большому количеству распределений отказов. Как правило, если коэффициент â или параметр формы меньше 1,0, распределение демонстрирует отклонения по раннему возрасту или младенческой смертности. Если параметр формы превышает примерно 3,5, данные зависят от времени и указывают на неисправности, связанные с износом.

Этот набор данных обычно предполагает гауссово или нормальное распределение. Когда коэффициент â увеличивается выше ~ 3,5, колоколообразное распределение сужается, демонстрируя увеличивающийся эксцесс (пик в верхней части кривой) и меньшее стандартное отклонение. Многие наборы данных содержат два или даже три отдельных региона.

Инженеры по надежности обычно строят, например, одну кривую, представляющую параметр формы во время обкатки, а другую кривую - постоянную или постепенно увеличивающуюся интенсивность отказов. В некоторых случаях появляется третий отчетливый линейный наклон, чтобы определить третью форму, область износа.

В этих случаях PDF-файл с данными об отказах действительно принимает знакомую форму кривой ванны (рис. 6). Однако большая часть механического оборудования, используемого на заводах, демонстрирует область младенческой смертности и область постоянной или постепенно увеличивающейся интенсивности отказов. Редко можно увидеть кривую, отображающую износ. Характерный срок службы, или η (нижний регистр греческого «эта»), является приближением Вейбулла для MTBF. Это всегда функция времени, миль или циклов, когда 63,21% оцениваемых устройств вышли из строя, что является MTBF / MTTF для экспоненциального распределения.

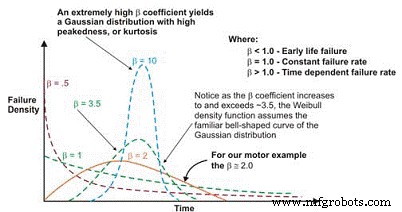
Рис. 6. В зависимости от параметра формы плотность отказов Weibull Curve может принимать несколько распределений, что делает его таким универсальным для проектирования надежности.

В качестве предостережения, чтобы связать этот инструмент с превосходным качеством обслуживания и операций, если бы мы могли более эффективно контролировать функции форсирования, которые приводят к механическому отказу в подшипниках, шестернях и т. Д., Такие как смазка, контроль загрязнения, выравнивание, балансировка, надлежащая эксплуатация и т. д., больше машин фактически дойдут до своего усталостного ресурса. Машины, которые достигли своего усталостного ресурса, будут демонстрировать знакомую характеристику износа.

Использование коэффициента β для корректировки уравнения интенсивности отказов как функции времени дает следующее общее уравнение:

Где:
h (t) =Интенсивность отказов (или степень опасности) в течение заданного времени (t)
e =Основание натурального логарифма (2,718281828)
θ =Расчетное среднее время безотказной работы / MTTF
β =Параметр формы Вейбулла из графика.

И следующая функция надежности:

Где:
R (t) =Оценка надежности за период времени, циклы, мили и т. Д. (T)
e =Основание натурального логарифма (2,718281828)
θ =Расчетное среднее время безотказной работы / MTTF
β =Параметр формы Вейбулла из графика.

И следующая функция плотности вероятности (pdf):

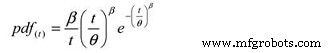
Где:
pdf (t) =Оценка функции плотности вероятности для периода времени,
циклов, миль и т. Д. (T)
e =Основание натурального логарифма (2,718281828)
θ =Расчетное среднее время безотказной работы / MTTF
β =Параметр формы Вейбулла из графика.

Следует отметить, что когда β равно 1,0, распределение Вейбулла принимает форму экспоненциального распределения, на котором оно основано.

Для непосвященного математика, необходимая для выполнения анализа Вейбулла, может показаться сложной. Но как только вы поймете механику формул, математика действительно будет довольно простой. Более того, программное обеспечение сделает большую часть работы за нас сегодня, но важно иметь понимание лежащей в основе теории, чтобы инженер по надежности предприятия мог эффективно использовать мощную технику анализа Вейбулла.

В нашем ранее рассмотренном примере электродвигателей мы ранее предполагали экспоненциальное распределение. Однако, если анализ Вейбулла выявил отказы на ранних этапах жизни, дав параметр формы β, равный 0,5, оценка надежности через шесть лет составила бы ~ 46%, а не ~ 55%, предполагая экспоненциальное распределение. Чтобы уменьшить количество отказов из-за износа, нам нужно будет полагаться на наших поставщиков, чтобы они обеспечивали более качественную и надежную сборку и поставку, лучше хранили двигатели, чтобы избежать ржавчины, коррозии, истирания и других механизмов статического износа, а также лучше выполнять установку. и запуск новых или восстановленных машин.

И наоборот, если анализ Вейбулла показал, что двигатели демонстрируют отказы, связанные в основном с износом, что дает параметр формы β, равный 5,0, оценка надежности через шесть лет будет ~ 93% вместо ~ 55%, предполагающих экспоненциальное распределение. Для зависящих от времени отказов из-за износа мы можем выполнить плановый капитальный ремонт или замену, предполагая, что у нас есть хорошая оценка MTBF / MTTF после того, как мы достигли области износа, и достаточно небольшое стандартное отклонение, чтобы с высокой степенью уверенности принимать решения о восстановлении / замене, которые не слишком дорогостоящие.

В нашем примере с двигателем, предполагая, что параметр формы β равен 5,0, частота отказов начинает быстро расти примерно через пять или шесть лет, поэтому мы можем захотеть отредактировать наши данные, чтобы сосредоточиться только на области износа при оценке замены или восстановления на основе времени. время. В качестве альтернативы, мы можем улучшить конструкцию, ориентируясь на доминирующий (ые) режим (ы) отказа, с целью уменьшения интерференции «напряжение-сила». Другими словами, мы можем попытаться устранить недостатки машины путем модификации конструкции, цель которой - устранить все, что вызывает зависящие от времени отказы.

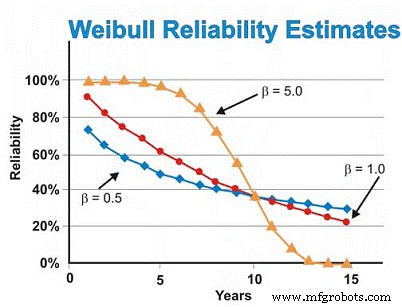
Предполагая, что все является постоянным, за исключением параметра формы β, на рисунке 7 показано различие, которое параметр формы β имеет при оценке надежности, предполагая, что значения формы β равны 0,5 (ранний срок эксплуатации), 1,0 (постоянный или экспоненциальный) и 5,0 (износ) для диапазон оценок времени. Этот рисунок наглядно иллюстрирует концепцию увеличения риска в зависимости от времени (β =0,5), постоянного риска в зависимости от времени (β =1,0) и увеличения риска в зависимости от времени (β =5).

Рис. 7. Различные прогнозы надежности как функция времени для разных Параметры формы Вейбулла

График Вейбулла с несколькими уклонами

Часто при рисовании наиболее подходящей линии регрессии через точки данных на графике Вейбулла коэффициент корреляции низкий, что означает, что фактические точки данных сильно отклоняются от линии регрессии. Это оценивается путем изучения коэффициента корреляции R или, более консервативно, R2, который обозначает изменчивость данных. Когда корреляция плохая, инженер по надежности должен изучить данные, чтобы оценить, существуют ли две или более закономерности, которые могут обозначать основные различия в режимах отказа, рабочем контексте и т. Д. Часто это дает две или более оценок бета (рисунок 8).

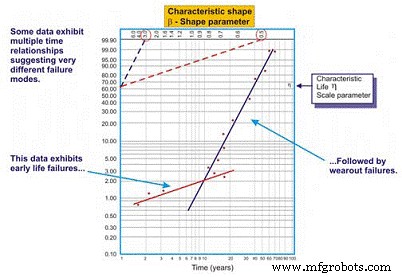
Рисунок 8. Пример диаграммы Вейбулла для нескольких бета-версий

Как мы видим в нашем примере на рисунке 8, набор данных работает лучше, когда нарисованы две различные линии регрессии. Первая строка показывает параметр бета-формы 0,5, что указывает на неудачи в раннем возрасте. Вторая линия имеет бета-форму 3,0, что говорит о том, что риск отказа увеличивается как функция времени. Для сложного оборудования, особенно механического, часто возникают отказы из-за обкатки, когда оно новое или недавно восстановленное. Таким образом, риск отказа наиболее высок сразу после первого запуска.

После того, как система проработает период обкатки, который может занимать минуты, часы, дни, недели, месяцы или годы, в зависимости от типа системы, система переходит к другому шаблону риска. В этом примере система входит в период, когда риск отказа возрастает как функция времени после выхода системы из периода обкатки.

Мульти-бета предлагает инженеру по надежности более точную оценку риска как функции времени. Вооружившись этими знаниями, он или она сможет лучше принять меры по смягчению последствий. Например, в ранний период жизни мы были бы склонны повышать точность, с которой мы производим / перестраиваем, устанавливаем и запускаем. Более того, мы можем добавить методы мониторинга и / или увеличить частоту мониторинга в период высокого риска. После периода обкатки мы могли бы внедрить методы мониторинга, нацеленные на зависящие от времени отказы изнашивания, которые, как считается, влияют на систему, соответственно увеличить частоту мониторинга или в некоторых случаях запланировать «жесткие» профилактические действия по техническому обслуживанию.

Оценка надежности системы

После того, как надежность компонентов или машин была установлена ​​относительно условий эксплуатации и требуемого времени выполнения миссии, инженеры предприятия должны оценить надежность системы или процесса. Опять же, для краткости и простоты, мы обсудим оценки надежности системы для последовательной, параллельной и резервированной системы с распределенной нагрузкой (r / n-системы).

Серийные системы
Прежде чем обсуждать серийные системы, следует обсудить блок-схемы надежности. Не сложный в использовании инструмент, блок-схемы надежности просто отображают процесс от начала до конца. Для последовательной системы за подсистемой A следует подсистема B и так далее. В последовательной системе возможность использования Подсистемы B зависит от рабочего состояния Подсистемы A. Если Подсистема A не работает, система не работает независимо от состояния Подсистемы B (Рисунок 9).

To calculate the system reliability for a serial process, you only need to multiply the estimated reliability of Subsystem A at time (t) by the estimated reliability of Subsystem B at time (t). The basic equation for calculating the system reliability of a simple series system is:

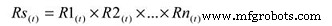
Where:
Rs(t) – System reliability for given time (t)
R1-n(t) – Subsystem or sub-function reliability for given time (t)

So, for a simple system with three subsystems, or sub-functions, each having an estimated reliability of 0.90 (90%) at time (t), the system reliability is calculated as 0.90 X 0.90 X 0.90 =0.729, or about 73%.

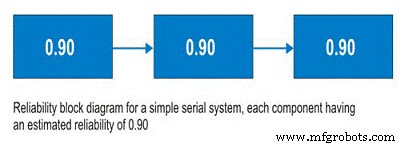
Figure 9. Simple Serial System

Parallel Systems
Often, design engineers will incorporate redundancy into critical machines. Reliability engineers call these parallel systems. These systems may be designed as active parallel systems or standby parallel systems. The block diagram for a simple two component parallel system is shown in Figure 10.

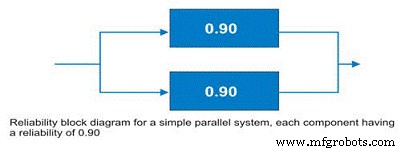
Figure 10. Simple parallel system – the system reliability is increased to 99% due to the redundancy.

To calculate the reliability of an active parallel system, where both machines are running, use the following simple equation:

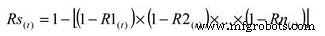
Where:
Rs(t) – System reliability for given time (t)
R1-n(t) – Subsystem or sub-function reliability for given time (t)

The simple parallel system in our example with two components in parallel, each having a reliability of 0.90, has a total system reliability of 1 – (0.1 X 0.1) =0.99. So, the system reliability was significantly improved.

There are some shortcut methods for calculating parallel system reliability when all subsystems have the same estimated reliability. More often, systems contain parallel and serial subcomponents as depicted in Figure 11. The calculation of standby systems requires knowledge about the reliability of the switching mechanism. In the interest of simplicity and brevity, this topic will be reserved for a future article.

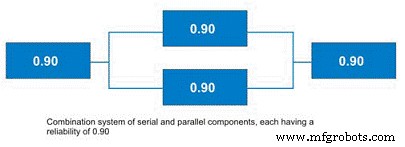
Figure 11. Combination System with Parallel and Serial Elements

r out of n Systems (r/n Systems)
An important concept to plant reliability engineers is the concept of r/n systems. These systems require that r units from a total population in n be available for use. A great industrial example is coal pulverizers in an electric power generating plant. Often, the engineers design this function in the plant using an r/n approach. For instance, a unit has four pulverizers and the unit requires that three of the four be operable to run at the unit’s full load (see Figure 12).

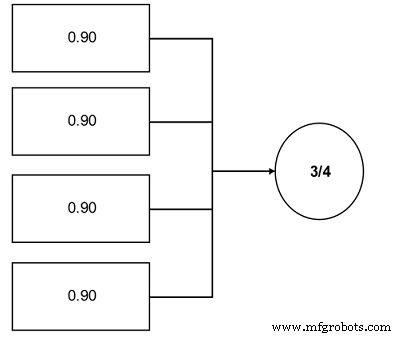
Figure 12. Simple r/n system example – Three of the four components are required.

The reliability calculation for an r/n system can be reduced to a simple cumulative binomial distribution calculation, the formula for which is:

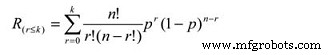
Where:
Rs =System reliability given the actual number of failures (r) is less than or equal the maximum allowable (k)
r =The actual number of failures
k =The maximum allowable number of failures
n =The total number of units in the system
p =The probability of survival, or the subcomponent reliability for a given time (t).

This equation is somewhat more complicated. In our pulverizer example, assuming a subcomponent reliability of 0.90, the equation works out as a summation of the following:
P(0) =0.6561
P(1) =0.2916

So, the likelihood of completing the mission time (t) is 0.9477 (0.6561 + 0.2916), or approximately 95%.

Field Data Collection
To employ the reliability analysis methods described herein, the engineer requires data. It is imperative to establish field data collection systems to support your reliability management initiatives. Likewise, as much as possible, you’ll want to employ common nomenclature and units so that your data can be parsed effectively for more detailed analysis. Collect the following information:

• Basic System Information
• Operating Context
• Environmental Context
• Failure Data

A good general system for data collection is described in the IEC standard 300-3-2. In addition to providing instructions for collecting field data, it provides a standard taxonomy of failure modes. Other taxonomies have been established, but the IEC standard represents a good starting point for your organization to define its own. Likewise, DOE standard NE-1004-92 offers a very nice standard nomenclature of failure causes.

An important benefit derived from your efforts to collect good field data is that it enables you to break the “random trap.” As I mentioned earlier, the bathtub curve has been much maligned – particularly in the Reliability-Centered Maintenance literature. While it’s true that Weibull analysis reveals that few complex mechanical systems exhibit time-dependent wearout failures, the reason, at least in part, is due to the fact that the reliability of complex systems is affected by a wide variety of failure modes and mechanisms.

When these are lumped together, there is a “randomizing” effect, which makes the failures appear to lack any time dependency. However, if the failure modes were analyzed individually, the story would likely be very different (Figure 13). For certain, some failure modes would still be mathematically random, but many, and arguably most, would exhibit a time dependency. This kind of information would arm reliability engineers and managers with a powerful set of options for mitigating failure risk with a high degree of precision. Naturally, this ability depends upon the effective collection and subsequent analysis of field data.

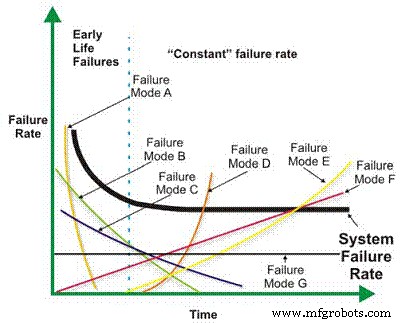
Figure 13. Good field data collection enables you to break the random trap.

This brief introduction to reliability engineering methods is intended to expose the otherwise uninitiated plant engineer to the world of quantitative reliability engineering. The subject is quite broad, however, and I’ve only touched on the major reliability methods that I believe are most applicable to the plant engineer. I encourage you to further investigate the field of reliability engineering methods, concentrating on the following topics, among others:

• More detailed understanding of the Weibull distribution and its applications

• More detailed understanding of the exponential distribution and its applications

• The Gaussian distribution and its applications

• The log-normal distribution and its applications

• Confidence intervals (binomial, chi-square/Poisson, etc.)

• Beta distribution and its applications

• Bayesian applications of reliability engineering methods

• Stress-strength interference analysis

• Testing options and their applicability to plant reliability engineering

• Reliability growth strategies and management

• More detailed understanding of field data collection.

Most important, spend time learning how to apply reliability engineering methods to plant reliability problems. If your interest in reliability engineering methods is high, I encourage you to pursue professional certification by the American Society for Quality as a reliability engineer (CRE).

References
Troyer, D. (2006) Strategic Plant Reliability Management Course Book, Noria Publishing, Tulsa, Oklahoma.

Bernowski, K (1997) “Safety in the Skies,” Quality Progress , January.

Dovich, R. (1990) Reliability Statistics, ASQ Quality Press, Milwaukee, WI.

Krishnamoorthi, K.S. (1992) Reliability Methods for Engineers, ASQ Quality Press , Milwaukee, WI.

MIL Standard 721

IEC Standard 300-3-3

DOE Standard NE-1004-92

Appendix:Select reliability engineering terms from MIL STD 721
Availability – A measure of the degree to which an item is in the operable and committable state at the start of the mission, when the mission is called for at an unknown state.

Capability – A measure of the ability of an item to achieve mission objectives given the conditions during the mission.

Dependability – A measure of the degree to which an item is operable and capable of performing its required function at any (random) time during a specified mission profile, given the availability at the start of the mission.

Failure – The event, or inoperable state, in which an item, or part of an item, does not, or would not, perform as previously specified.

Failure, dependent – Failure which is caused by the failure of an associated item(s). Not independent.

Failure, independent – Failure which occurs without being caused by the failure of any other item. Not dependent.

Failure mechanism – The physical, chemical, electrical, thermal or other process which results in failure.

Failure mode – The consequence of the mechanism through which the failure occurs, i.e. short, open, fracture, excessive wear.

Failure, random – Failure whose occurrence is predictable only in the probabilistic or statistical sense. This applies to all distributions.

Failure rate – The total number of failures within an item population, divided by the total number of life units expended by that population, during a particular measurement interval under stated conditions.

Maintainability – The measure of the ability of an item to be retained or restored to specified condition when maintenance is performed by personnel having specified skill levels, using prescribed procedures and resources, at each prescribed level of maintenance and repair.

Maintenance, corrective – All actions performed, as a result of failure, to restore an item to a specified condition. Corrective maintenance can include any or all of the following steps:localization, isolation, disassembly, interchange, reassembly, alignment and checkout.

Maintenance, preventive – All actions performed in an attempt to retain an item in a specified condition by providing systematic inspection, detection and prevention of incipient failures.

Mean time between failure (MTBF) – A basic measure of reliability for repairable items:the mean number of life units during which all parts of the item perform within their specified limits, during a particular measurement interval under stated conditions.

Mean time to failure (MTTF) – A basic measure of reliability for non-repairable items:The mean number of life units during which all parts of the item perform within their specified limits, during a particular measurement interval under stated conditions.

Mean time to repair (MTTR) – A basic measure of maintainability:the sum of corrective maintenance times at any specified level of repair, divided by the total number of failures within an item repaired at that level, during a particular interval under stated conditions.

Mission reliability – The ability of an item to perform its required functions for the duration of specified mission profile.

Reliability – (1) The duration or probability of failure-free performance under stated conditions. (2) The probability that an item can perform its intended function for a specified interval under stated conditions. For non-redundant items this is the equivalent to definition (1). For redundant items, this is the definition of mission reliability.