Спин и орбитальное вращение плазмонного димера под действием циркулярно поляризованного света

Фон

Оптическое связывание двух микрочастиц (MP) или наночастиц (NP), облучаемых линейно поляризованным (LP) светом, является важным оптомеханическим поведением, которое является результатом взаимодействия света с веществом [1,2,3,4]. Между оптически связанным димером существует несколько стабильно равновесных межчастичных расстояний; эти расстояния почти целые кратные длины волны в среде [3,4,5,6]. Кроме того, ориентация димера перпендикулярна поляризации света LP. Поскольку расстояние между частицами близко к целым числам, кратным длине волны, рассеянные фотоны между частицами создают конструктивную интерференцию, чтобы вызвать связывающую силу. Также были изучены явления оптически связанного массива из множества МП кремнезема или НЧ Ag [7,8,9,10]. Для освещения плоской волны с круговой поляризацией (CP) Haefner et al. сообщили, что спиральность продольного спина и орбитального вращения двух связанных наночастиц кремнезема размером 100–700 нм совпадает с направленностью падающего света [11]. Недавно Sule et al. экспериментально обнаружено, что спиральность орбитального вращения двух НЧ Ag радиусом 75 нм, связанных оптической силой, противоположна направленности сфокусированного гауссова пучка СР длиной 790 нм в воде [12]; т.е. димер Ag испытывает отрицательный оптический орбитальный момент [13, 14]. Кроме того, измеренное вращение орбиты составило около 4 кГц [12]. С другой стороны, спин одиночной Au NP радиусом 100 нм, индуцированный CP-гауссовым пучком, также изучался [15,16,17,18]. Измеренное вращение спина достигло 3,5 кГц [15]. В последние десятилетия продольное / поперечное спин-орбитальное взаимодействие (SOC) оптического поля привлекает большое внимание [19,20,21,22,23]. Например, оптический вихревой пучок (например, пучки Лагерра-Гаусса высокого порядка с азимутальной или радиальной поляризацией) или сильно сфокусированный CP-гауссов пучок можно использовать для индукции SOC [24,25,26,27,28,29,30 , 31,32,33,34]. Закрученное электромагнитное (ЭМ) поле оптического вихревого луча несет как спиновой, так и орбитальный угловой момент, тем самым вызывая продольный / поперечный спин и орбитальное вращение близлежащей зондирующей НЧ [18,19,20,21,22,23 , 24,25,26]. В частности, SOC в ближней зоне НЧ Au или Ag более значим из-за коллективного движения свободных электронов в этих НЧ (плазмонный эффект) [28,29,30,31].

В этой статье мы теоретически исследуем оптомеханическое поведение (оптические силы и моменты) двух связанных наночастиц золота (димеров), поддерживаемых подложкой, которые индуцируются освещением гауссова пучка CP. Подложка необходима для ограничения этих автономных НЧ, движущихся в фокальной плоскости, вместо того, чтобы парить в трехмерном пространстве. Метод множественных мультиполей (MMP) используется для численного моделирования электромагнитного поля, а затем для анализа оптических орбитальных и спиновых моментов на оптически связанном димере [35, 36]. Через оптомеханические реакции димера будет проявляться продольный / поперечный SOC. В частности, также будет исследовано условие создания отрицательного оптического орбитального момента на димере.

Методы

На рисунке 1 показана конфигурация пары идентичных наночастиц Au, поддерживаемых подложкой и облучаемых нормально падающим левосторонним (LH) CP-светом (плоская волна или гауссов пучок), где d представляет собой расстояние между частицами. Перетяжка гауссова луча обозначается w ₀ , а фокальная плоскость находится в центральном сечении НЧ Au. Формулировки электрического поля плоской волны и гауссова пучка прилагаются в Приложении. Мы предполагаем, что показатель преломления подложки такой же, как и у окружающей среды - воды. Следовательно, отраженный свет не будет индуцироваться на границе раздела между средой и подложкой; оптическое поле не нарушается наличием подложки [37]. С другой стороны, наличие субстрата служит ограничением для поддержки НЧ, движущихся по субстрату. Метод множественных мультиполей (ММП) используется для моделирования индуцированного электромагнитного поля [17, 18, 35, 36]. Оптические силы F ^j на j й НП ( j =1, 2) выражаются

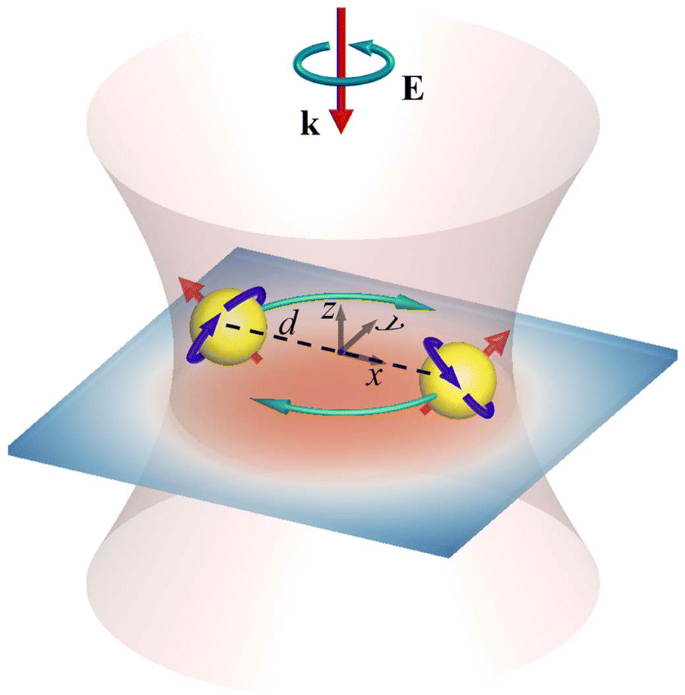
Конфигурация пары НЧ с поддерживающей подложкой, облученных нормально падающим гауссовым пучком перетяжки LH CP (w0). Центральные сечения этих НЧ находятся в фокальной плоскости гауссова пучка, а d - расстояние между центрами НЧ. Оптомеханические реакции - продольное орбитальное вращение и продольное / поперечное вращение

Здесь n вектор внешней нормали на поверхности j th NP и T - тензор напряжений Максвелла, усредненный по времени, выраженный как

В формуле. (2), Я представляет собой единичную матрицу 3 × 3, черта сверху обозначает комплексно сопряженную матрицу, а Re - действительную часть [17, 18, 35, 36]. Здесь ε и μ - диэлектрическая проницаемость и проницаемость окружающей среды. Обратите внимание, что E и H - внешнее полное поле, используемое для уравнения. (2). Фактически, T также является усредненным по времени потоком линейного импульса. В этой статье оптические силы выражаются в цилиндрических координатах:радиальная, азимутальная и z -осевые компоненты. Радиальная сила может определять притяжение или отталкивание между двумя НЧ, а азимутальная сила - спиральность орбитального вращения НЧ.

С другой стороны, оптический вращающий момент на j й НП ( j =1, 2) для раскрутки отдельных НП определяется как,

В формуле. (3), x ^j × Т - поток углового момента, а x ^j вектор относительного положения точки x на поверхности S _j относительно центра масс \ ({\ mathbf {x}} _ c ^ j \) точки j й НП; \ ({\ mathbf {x}} ^ j =\ mathbf {x} - {\ mathbf {x}} _ c ^ j \). Продольное направление должно быть параллельным оптической оси (скажем, z направление) падающего света, а поперечное направление перпендикулярно оптической оси. С другой стороны, продольный оптический орбитальный момент в z направление на каждую НП, вызванное азимутальной оптической силой, определяется как F _θ г / 2 в цилиндрических координатах. Относительная диэлектрическая проницаемость Au при λ =800 нм, используемое в моделировании, составляет (- 24,062, 1,507) [38].

Результаты и обсуждение

Мы изучаем оптические силы и моменты, действующие на две идентичные наночастицы Au с радиусом 100 нм, облучаемые нормально падающей плоской волной LH CP или сфокусированным гауссовым пучком в фокальной плоскости. Окружающая среда - вода. Плотность энергии плоской волны или гауссова пучка в центре составляет 25 МВт / см ² . . Центры двух отдельно стоящих NP, поддерживаемых виртуальной подложкой, могут перемещаться в xy плоскость (фокальная плоскость). Оптические силы ( F _r , F _θ ) от межчастичного расстояния d для плоской CP-волны или сфокусированного гауссова пучка с перетяжкой 500 нм λ =800 нм показаны на рис. 2а, б соответственно. Центральное сечение этих НЧ находится в фокальной плоскости гауссова пучка. Рисунок 2a показывает, что для плоской волны существует несколько устойчиво-равновесных межчастичных расстояний с F _r =0 и отрицательный наклон; первый d ₁ находится на 603 нм, а второй - d ₂ на 1204 нм. Эти «стабильно-равновесные» межчастичные расстояния почти целые числа, кратные длине волны в среде; т.е. d _м = mλ / н , где n - показатель преломления среды и м =1, 2, 3 ... Это результат дальнодействующего взаимодействия света и вещества, вызванного оптической связующей силой. Это предполагает наличие оптической пружины, соединяющей две НЧ; восстанавливающая сила F _r оптической пружины удерживает НЧ друг от друга на этих устойчивых равновесных межчастичных расстояниях. В случае гауссова пучка первые два устойчивых равновесных межчастичных расстояния d ₁ и d ₂ равны 585 и 1131 нм соответственно, как показано на рис. 2b, что немного меньше, чем у плоской волны, из-за градиентной силы, индуцированной гауссовым лучом.

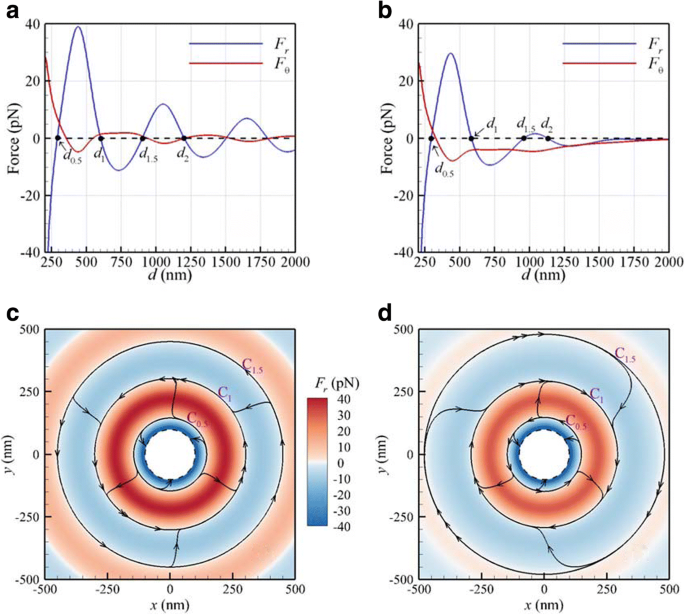
Оптические силы ( F _r , F _θ ) по сравнению с d для λ =800 морских миль по CP a плоская волна и b Гауссов пучок с перетяжкой 500 нм в фокальной плоскости. 2D карты линий тока оптической силы ( F _r , F _θ ) индуцированный CP c плоская волна и d Гауссов пучок. Цветная полоса представляет собой амплитуду F _r . Пунктирное кольцо - это предельная окружность центров двух НЧ, где НЧ находятся в контакте

Фактически, продольный орбитальный момент F _θ г / 2 заставит эти НЧ вращаться по орбитам с диаметром d ₁ и d ₂ . Для случаев с гауссовым пучком орбиты будут центрированы на оси пучка. Знак азимутальной оптической силы ( F _θ ) указывает на то, что продольное орбитальное вращение (оборот) на первой устойчиво-равновесной орбите, индуцированное гауссовым пучком, противоположно вращению плоской волны. Это показывает, что отрицательный F _θ Гауссова пучка CP создает отрицательный орбитальный момент F _θ г ₁ / 2 на первой устойчиво-равновесной орбите; что более важно, спиральность орбитального вращения димера Au противоположна направленности падающего CP-света [12]. Также интересно отметить, что F _θ всегда отрицательно как d > 300 нм для случаев с гауссовым пучком; Явление обратного вращения (вращения) оптически связанных НЧ из-за отрицательного орбитального момента легко наблюдается в системах оптических пинцетов. Отрицательный оптический орбитальный момент может быть объяснен закрученным электромагнитным полем гауссова пучка [23].

Согласно закону Стокса сферы, движущейся силой F для движения в вязкой жидкости конечная скорость v _Т составляет v _Т = F / (6 πrη ), где η - динамическая вязкость воды (0,001 кг / м с). Это результат приложенной силы, уравновешенной силой сопротивления вязкой жидкости [39]. Согласно закону Стокса, вектор конечной скорости НЧ в вязкой среде пропорционален приложенной силе [39]. Следовательно, мы использовали поле оптических сил для получения линий тока, которые почти эквивалентны траекториям этих НЧ. Кроме того, двухмерные карты линий тока, полученные непосредственно из поля вектора оптической силы ( F _r , F _θ ), воздействующие на НЧ, показаны на рис. 2c, d для плоской волны и гауссова луча соответственно, где цветная полоса представляет амплитуду F _r . Обратите внимание, что касательная к линии тока в каждой точке тогда параллельна вектору оптической силы и, следовательно, также параллельна скорости NP. Для небольшого диапазона расстояний между частицами ( d < г _0,5 ) радиальная оптическая сила F _r отрицательна, поэтому эти два NP будут притягиваться друг к другу и в конечном итоге столкнуться, как показано на рис. 2c, d. Пунктирное кольцо - это предельная окружность центров двух НЧ, где НЧ находятся в контакте. Внутреннее кольцо (синее) - это область ближнего взаимодействия. Внутреннее кольцо C _0,5 между внутренним кольцом (синий, с отрицательным значением F _r ) и второе кольцо (красное, с положительным значением F _r ) - граница между областями ближнего и дальнего взаимодействия димера Au; диаметр C _0,5 это d _0,5 =291 нм на рис. 2c и d _0,5 =296 нм на рис. 2г. В большом диапазоне ( d _0,5 < г < г _1.5 ) радиальные и азимутальные оптические силы заставляют две связанные НЧ приближаться к первой стабильно-равновесной орбите C ₁ диаметром d ₁ за счет эффекта оптической силы связи. Оптически связанный димер Au вращается против часовой стрелки (CCW) по орбите C ₁ ( г ₁ =603 нм) на рис. 2в, а вдоль C ₁ ( г ₁ =585 нм) по часовой стрелке (CW) на рис. 2г. Первое вращение такое же, как вращение падающего света, вызванное положительным орбитальным моментом ( F _θ > 0), а последнее - обратное из-за отрицательного орбитального момента ( F _θ <0). Согласно нашему анализу спектра поперечного сечения рассеяния димера с расстоянием стабильного равновесия 603 нм, облученного плоской CP-волной (здесь не показана), поверхностный плазмонный резонанс связи (SPR) оптически связанного димера почти равен 800 нм соответствует падающему свету, который находится вне резонанса одиночной НЧ (530 нм). В общем, SPR связи димера зависит от расстояния между частицами; чем больше расстояние, тем больше сдвигается в красную область ППР связи димера. Если мы используем более длинноволновый гауссов пучок (например, 1064 нм), расстояние между частицами в устойчивом равновесии увеличивается. Однако по мере того, как расстояние между двумя NP становится слишком большим, эффект оптической связи уменьшается, так что SPR связи постепенно исчезает. Следовательно, SPR одиночной наночастицы на длине волны 530 нм становится доминирующим.

Для Au NP радиусом 100 нм, которая движется по орбите с диаметром d и угловой скоростью Ω _z , скорость равна Ω _z г / 2 = F _θ / ( 6πrμ ). Если применяется гауссов луч ( F _θ =- 4 пН), угловая скорость Ω _z (циклов в секунду) вдоль C ₁ около - 7 кГц. Порядок величины согласуется с экспериментальным результатом [12]; угловая скорость орбитального вращения двух НЧ Ag r =75 нм при облучении гауссовым пучком мощностью 14 мВт составляет - 4 кГц. Если d _1.5 < г < г _2,5 , эти НЧ будут сближаться и вращаться по вторичной стабильно-равновесной орбите C ₂ (здесь не показано). Обратите внимание, что для этих случаев оптическая сила F _z отрицательно, чтобы подтолкнуть эти НЧ вниз по потоку из-за радиационного давления; F _z =- 161,3 пН для плоской волны и - 117,2 пН для гауссова пучка. Это означает, что сила реакции от поддерживающей подложки необходима для уравновешивания движущей оптической силы F _z . Следовательно, равнодействующие силы в z направление на эти NP равно нулю; эти два NP ограничены перемещением в xy плоскость фокальной плоскости.

С другой стороны, на рис. 3a, b показаны оптические вращающие моменты ( M _r , M _θ , M _z ) по сравнению с d индуцированный плоской волной и гауссовым пучком в фокальной плоскости соответственно. Поскольку результаты этих двух НП одинаковы, здесь показан только набор оптических вращающих моментов. Первые два ( M _r , M _θ ) - поперечные спиновые моменты, а последние M _z продольный. Обнаружено, что спиральность продольного крутящего момента такая же, как и направленность падающего света для обоих случаев. Это связано с тем, что угловой момент поглощенных фотонов падающего CP-света передается этим NP для вращения и орбитального вращения. Интересно отметить, что поперечные оптические вращающие моменты ( M _r , M _θ ), индуцированные гауссовым пучком, значительно велики по сравнению с таковыми от плоской волны. Это может быть связано с поперечными составляющими скрученного электромагнитного поля в фокальной плоскости гауссова пучка. Более того, максимальные значения оптических поперечных вращающих моментов примерно наблюдаются на первой стабильно-равновесной орбите C ₁ ( г ₁ =585 нм), как показано на рис. 3б. Согласно закону Стокса вращающаяся сфера, вращаемая с крутящим моментом M в вязкой жидкости конечная угловая скорость сферы равна ω _Т = M / (8 πr ³ μ ) [18]. Следовательно, величины продольных / поперечных угловых скоростей спина НЧ при C ₁ составляют около 10 кГц, из которых по порядку величины согласуются с измеренной продольной скоростью спина [15], около 3,5 кГц. Вкратце, вышеупомянутые явления, как показано на фиг. 2b и 3b демонстрируют, что продольное орбитальное вращение сопровождается продольными / поперечными спинами. Движение двух связанных НЧ аналогично движению системы двойной звезды, где оптические силы обеспечивают связывающие и орбитальные движущие силы для этих НЧ, а оптические вращающие моменты вызывают их вращение.

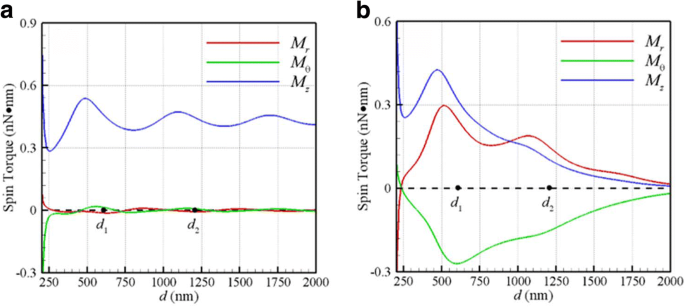
Оптический вращающий момент ( M _r , M _θ , M _z ) по сравнению с d при λ =800 нм для a плоская волна и b Гауссов пучок с w ₀ =500 нм в фокальной плоскости

Кроме того, можно настроить диафрагму объекта оптического пинцета, чтобы изменить размер падающего луча, тем самым изменяя числовую апертуру и перетяжку гауссова луча. На рисунке 4а показан оптический орбитальный момент F . _θ г / 2 на двух связанных НЧ Au радиусом 100 нм, вращающихся на соответствующей первой стабильно-равновесной орбите ( d = d ₁ ) по сравнению с перетяжкой гауссова пучка CP с длиной λ =800 нм. Соответствующее первое расстояние устойчивого равновесия d ₁ также нанесен на рис. 4a (масштабная линейка справа), где плоскую волну можно рассматривать как частный случай w ₀ → ∞. Точка поворота перетяжки гауссова луча между положительным и отрицательным орбитальными моментами находится на 1150 нм, что соответствует F _θ =0, как показано на рис. 4а. Чем меньше перетяжка гауссова пучка, тем больше величина отрицательного орбитального момента. По мере увеличения талии d ₁ гауссова луча приближается к значению (603 нм) плоской волны ( w ₀ → ∞). В частности, по мере уменьшения перетяжки значения поперечных вращающих моментов ( M _r , M _θ ) в d ₁ значительно увеличится, при этом крутящий момент продольной раскрутки M _z уменьшается, как показано на рис. 4b. Эти результаты показывают, что перетяжка гауссова луча является ключевым фактором для создания отрицательного продольного орбитального момента и поперечных вращающих моментов из-за степени искажения электромагнитного поля.

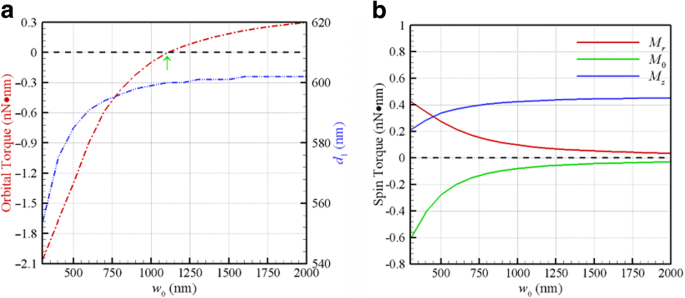
а Оптический орбитальный момент и d ₁ на первой стабильно-равновесной орбите относительно перетяжки гауссова пучка с длиной λ =800 нм. Точка поворота перетяжки для создания положительного или отрицательного орбитального момента находится на 1150 нм. б Оптические вращающие моменты в зависимости от талии при d ₁

Механизм отрицательного орбитального вращения и поперечного вращения этих НЧ можно объяснить ротором спинового углового момента светового поля, даже без вклада орбитального углового момента светового луча [23]. Благодаря характеристикам отрицательного продольного орбитального момента и поперечного спинового момента на димере Au может проявляться плазмонно-усиленный SOC фотонов. Кроме того, направления орбитального вращения димера и вращения отдельных НЧ зависят от направленности падающего света.

Выводы

Теоретически изучены оптомеханические отклики (оптические силы и моменты) пары наночастиц Au, облученных светом КП. Наши результаты показали, что устойчиво-равновесные орбиты их вращения (обращения) могут быть индуцированы для дальнодействующего взаимодействия; расстояния между частицами в устойчивом равновесии почти целые числа, кратные длине волны в среде. Азимутальная оптическая сила вызывает орбитальное вращение этих НЧ, а оптический крутящий момент вызывает их вращение, особенно поперечные компоненты. Это движение похоже на движение двойных звезд равной массы, движущихся по круговой орбите вокруг своего общего центра масс. Когда перетяжка гауссова луча меньше точки поворота, спиральность орбитального вращения оптически связанного димера Au противоположна направленности падающего CP-света. Кроме того, продольный / поперечный SOC становится значительным по мере уменьшения перетяжки гауссова пучка; следовательно, поперечный спин двух НЧ становится более глубоким. Для короткодействующего взаимодействия оптическая сила вызывает взаимное притяжение. Следовательно, две связанные плазмонные НЧ не только вращаются, но и вращаются по спиральной траектории и в конечном итоге столкнутся. Кроме того, граница межчастичного расстояния между дальнодействующим и ближним взаимодействиями двух связанных НЧ примерно находится на половине длины волны в среде. Наши результаты показали, что порядок величины оптической силы составляет около pN, что можно сравнить с другими силами (например, пондеромоторной силой), чтобы определить вклад в движение НЧ. Наше открытие может проложить путь к применению SOC на НЧ, управляющих светом, в нанонауке и нанотехнологиях. Кроме того, стоит изучить корреляцию между оптическим спином и орбитальным крутящим моментом на двух НП и плотностями спинового и орбитального углового момента электромагнитного поля; первое определяется как \ (\ operatorname {Im} \ left (\ overline {\ mathbf {E}} \ times \ mathbf {E} \ right) / 2 \ omega \), а второе показано в Ref. [23]. Кроме того, стоит исследовать КПО в закрученной ближней зоне метаматериалов [40,41,42,43].

Сокращения

CP:

Круговая поляризация

EM:

Электромагнитный

LH:

Левша

LP:

Линейно поляризованный

MMP:

Множественный мультиполюс

MP:

Микрочастицы

NP:

Наночастицы

SOC:

Спин-орбитальная связь