Оценка накопления энергии суперконденсатором на основе дробно-дифференциальных уравнений

Фон

На сегодняшний день суперконденсаторы являются основными компонентами многих устройств и систем, например, систем резервного питания и рекуперации электроэнергии, а также автомобильных приложений, гибридных транспортных средств и многих других. Способность накапливать заряд без каких-либо химических реакций позволяет таким элементам иметь в сотни раз большее количество циклов заряда / разряда по сравнению с обычными батареями [1]. Кроме того, высокая скорость заряда / разряда делает их эффективными для приложений в системах рекуперации энергии, например, на транспорте или в возобновляемых источниках энергии [2, 3]. Во всех этих приложениях ключевым параметром является информация о количестве накопленной энергии в суперконденсаторе [4, 5]. К сожалению, хорошо известное соотношение для типичных конденсаторов, которое позволяет определить информацию, то есть (1/2) C U ² , не может быть использован [6]. Количество накопленной энергии нельзя определить только по напряжению на клеммах конденсатора. Основная причина этого - диффузионный процесс, связанный с перераспределением заряда [1, 7]. Вот почему многие исследователи пытались определить модель суперконденсатора, которая позволила бы оценить поведение реальной системы. В настоящее время исследователи в основном используют комбинации типичных электронных элементов, например, RC четырехполюсник или последовательно-параллельные комбинации таких элементов. Однако все эти модели предполагают взаимосвязь между током суперконденсатора и напряжением на его выводе в форме типичного дифференциального уравнения целочисленного порядка [3–5, 7].

Но оказывается, что некоторые совершенно новые возможности для оценки энергии в таких системах могут быть получены с применением дробного исчисления [8, 9]. Дифференциально-интегральное исчисление нецелого порядка было предложено более 300 лет назад, но важные вопросы реализации связаны с появлением компьютеров и их использованием при моделировании динамических систем с дискретным временем [10–14]. Применение дробного исчисления к проблеме оценки параметров суперконденсатора - не новая проблема. В этой области имеется множество публикаций [15–25]. Авторы выполняют задачу оценки параметров как в частотной, так и во временной областях [26].

Эта статья представляет собой расширенную версию презентации автора на конференции [27], в которой кратко представлен подход дробного порядка для оценки энергии, накопленной в суперконденсаторе.

Точная оценка параметров суперконденсаторов также крайне важна при оценке их надежности [28–31]. Постоянные процессы деградации внутри суперконденсатора могут изменить эквивалентное последовательное сопротивление и емкость. Таким образом, точное определение этих параметров, основанное на предлагаемом методе, также позволяет точно оценить производительность конденсатора.

Эта статья начинается с некоторых предварительных сведений, связанных с интегрированием и дифференцированием дробного порядка. Затем в нем представлен метод оценки параметров, используемый во время испытаний, и предлагается новый метод расчета энергии, основанный на дробном исчислении. В разделе «Результаты и обсуждение» представлены расчетные значения энергии для различных сценариев и их сравнение с эталонными (измеренными) значениями. Выводы и вклады кратко изложены в разделе «Выводы».

Методы

Использование пористых материалов в суперконденсаторах и особый способ накопления заряда приводят к тому, что традиционные подходы, основанные на моделях производной целого порядка, недостаточно точны. Многие исследователи предлагали различные решения в виде комбинации типовых RC элементы с постоянными или переменными значениями [4, 7]. Но оказывается, что определенно лучшую точность можно получить, используя дифференциальное исчисление нецелого порядка для определения соотношений между током и напряжением суперконденсатора [17, 19]. Кроме того, такое решение может привести к очень простой структуре модели, обеспечивая при этом очень высокую точность [18].

Дифферо-интегральное исчисление дробного порядка

Дифференциальное исчисление дробного порядка известно более 300 лет. Однако только последние несколько лет принесли ей популярность в моделировании физических явлений и процессов. Считается, что описание динамики с производной или интегралом нецелого порядка может быть одним из наиболее эффективных методов моделирования реальных свойств многих сложных явлений и промышленных процессов, особенно на основе новых материалов и технологий [10, 12, 13 , 32–34].

Дифференциальное или интегральное исчисление нецелочисленного порядка является обобщением классического исчисления до порядка α принадлежащий множеству действительных чисел \ (\ mathcal {R} \). Дифферно – интегральный оператор порядка \ (\ alpha \ in \ mathcal {R} \) функции f ( т ) в диапазоне [ a , t ] можно записать следующим образом

предполагая, что функция f ( т ) многократно дифференцируема и интегрируема. Что касается оператора (1), существует множество определений его реализации. Такие определения различаются свойствами и областями применения. Наиболее популярны определения Римана – Лиувилля, Капуто и Грюнвальда – Летникова (GL) [34]. Последний будет использован в этой статье в форме

где бином \ (\ alpha \ choose j \) определяется следующим образом

Чтобы получить дробную модель в дискретные моменты времени, определение GL в дискретной форме упрощается как

Существует несколько схем дискретизации уравнения GL. (4). К наиболее популярным относятся операторы обратных разностей (Эйлера), трапеции (Тастина) и Аль-Алауи. Используя метод Эйлера, дробная производная в дискретные моменты времени k можно представить как

Бесконечная сумма предыдущих выборок в реальных системах должна быть ограничена конечным значением из-за ограниченной памяти и ограниченного времени вычислений. Теперь усеченная или дискретная аппроксимация конечной длины GL имеет вид

где f ( l ) =0 для l <0 и L - длина модели (6) [23]. Уменьшение количества выборок приводит к снижению точности расчетов. Это важно для систем, работающих в непрерывном режиме. Некоторые другие виды решений представляют собой алгоритмы, аппроксимирующие дробные дифференциро-интегралы с моделями целого порядка. Примером могут служить рекурсивные фильтры Oustaloup [35]. Другой эффективной моделью конечной длины является FFLD, представляющая собой комбинацию усеченной модели (6) и разницы на основе Лагарра [24, 36, 37].

Все результаты идентификации, а также измерения энергии получены на основе всех выборок в (длинном) окне наблюдения L , т.е. с максимальной точностью. На рисунке 1 представлены ступенчатые характеристики интегрирования и дифференцирования, полученные на основе (6), для k =0,1,…, L и для различных значений порядка интегрирования / дифференцирования α . Предполагая разные значения порядка α можно более точно моделировать различные физические процессы, особенно диффузионные.

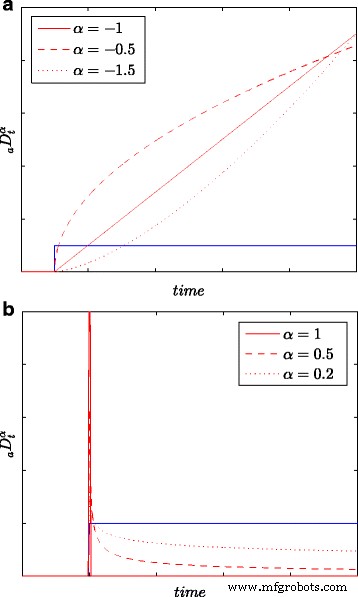
Шаговые ответы для интеграции ( a ) и дифференцирующий ( b ) модели с разным порядком α

Оценка параметров для дробной модели

Результаты всех измерений энергии и процедур идентификации, представленные в этой статье, были получены для суперконденсатора, заряженного от управляемого источника напряжения. В такой системе ток суперконденсатора i _C ( т ) должен быть ограничен резистором R соединены последовательно с суперконденсатором C (Рис. 2). Оценка всех параметров суперконденсатора производится на основе четырехполюсного отклика u _C ( т ) до ступени напряжения u ( т ) на его входе. Выбор подходящего значения производного порядка α позволяет учесть модель суперконденсатора физических явлений, связанных с диффузионными процессами, связанными с перераспределением заряда во время процессов зарядки и разрядки. Параллельный резистор r _P дополнительно позволяет моделировать ток утечки. Используя дробно-дифференциальное исчисление для моделирования суперконденсаторов, структура модели может иметь невысокую сложность. Для суперконденсатора, заряжаемого от источника напряжения, модель состоит всего из двух элементов, то есть простого RC четырехполюсник (рис. 2а). Для малых мощностей последовательное сопротивление r _S имеет значение (рис. 2б), а ток утечки I _L может быть дополнительно представлен параллельным сопротивлением r _P (Рис. 2в). Используя исчисление дробного порядка для моделирования суперконденсатора, соотношение между напряжением на выводах конденсатора и его током можно выразить следующим образом

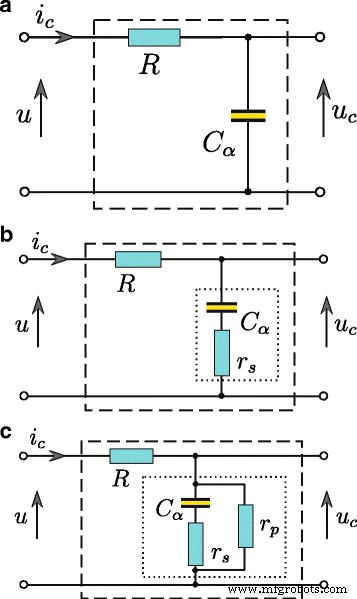
Суперконденсатор RC модели, базовая модель ( a ), расширенный последовательным сопротивлением ( b ), и с дополнительным параллельным сопротивлением ( c )

где оператор d ^α / d t ^α означает оператор дифференцирования порядка α и единица СИ - C _α равно [F / sec ^{1− α} ]. Базовая конфигурация суперконденсатора, представленная на рис. 2а, может рассматриваться как инерциальная система первого порядка и может быть представлена ​​дробной передаточной функцией

где T = R C _α . С учетом последовательного сопротивления r _S (Рис. 2b), схема рассматривается как система коррекции задержки по фазе с передаточной функцией (ср. [24])

где T ₁ = C _α ( R + r _S ) и T ₂ = r _S C _α . Кроме того, с учетом параллельного резистора r _P представляющий ток утечки I _L (Рис. 2c), передаточная функция системы может быть выражена как

где K = R / г _P +1, T ₁ = C ( R г _s / г _P + R + r _S ) и T ₂ = r _S C . Во временной области уравнение. (10) можно представить как

Временной отклик модели, определенной формулой (11), был получен путем преобразования ее в форму, графически представленную на рис. 3, где операции интегрирования и дифференцирования имеют дробный порядок α . Эта модель использовалась в процессе оценки параметров суперконденсатора. Идентификацию тестируемого суперконденсатора проводили с помощью системы, представленной на рис. 4а. Процедура управления всей системой была разработана с использованием программного обеспечения Matlab / Simulink с xPC Toolbox. Система состояла из настольного ПК (xPC Target) с установленной измерительной картой NI-DAQ и главного компьютера (xPC Host). Компьютеры были связаны через сеть Ethernet. Суперконденсатор заряжался и разряжался от источника (управляемого напряжением) напряжения (рис. 4б) с выходом по току до ± 3 А. Измерительная система работала с частотой дискретизации 100 Гц, при этом все измерения и аналоговые управляющие сигналы подавались. обрабатывается с разрешением 16 бит [25].

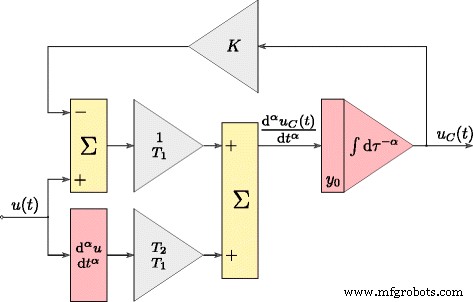
Структура Matlab модели суперконденсатора во временной области

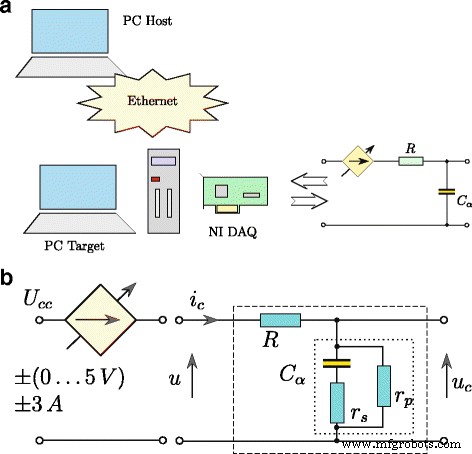
Структура системы измерения ( a ) и схему заряда / разряда суперконденсатора ( b )

Основной метод определения динамических свойств системы основан на анализе переходной характеристики [38]. Применительно к модели системы этот метод позволяет оценить ее параметры. Для этого исследования использовался ступенчатый сигнал с различными напряжениями (0,5 / 1,0 / 1,5 / 2,0 / 2,7 В) и постоянной длительностью (500 с) (см. Рис. 5 и таблицу 2). С другой стороны, одним из типичных применений суперконденсаторов является накопление или доставка энергии в энергосистемы. В этом случае скорость изменения напряжения довольно мала. Для его моделирования использовался сигнал 400 мВпик и 0,03 рад / с со смещением 2 В (рис. 6). Кроме того, чтобы изучить влияние изменений напряжения и частоты на расчетные параметры, были использованы различные значения последних (см. Таблицу 3).

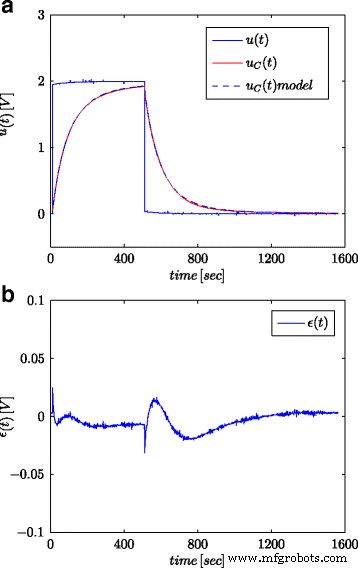
Переходные характеристики испытанного суперконденсатора и его дробной модели ( a ) и ошибка ответа модели ( b )

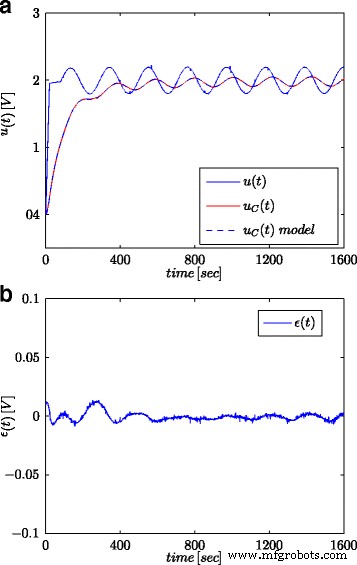
Синусоидальные волновые характеристики испытанного суперконденсатора и его дробной модели ( a ) и ошибка ответа модели ( b )

Существует несколько методов оценки параметров модели. Основная цель процедуры идентификации во временной области, примененной в данной работе, заключалась в оценке вектора неизвестных параметров θ =[ α , C _α , r _S , r _P ] дробной модели (11). Для минимизации начальной ошибки использовался метод наименьших квадратов. Критерий оптимизации включал минимизацию стандартной ошибки \ (\ | \ epsilon (k) \ | _ {2} ^ {2} \), где

где u _C ( к ) - выходное напряжение, измеренное от тестируемой системы в момент k , а \ (\ hat {u} _ {C} (k) \) - выходное напряжение из рассматриваемой модели для входного сигнала u ( к ). Проблема идентификации теперь сводится к нахождению вектора параметров θ ∈ Θ _{объявление} что минимизирует квадратный критерий J таким образом, чтобы

где Θ _{объявление} обозначает набор допустимых значений параметров, а N означает время моделирования. Существует множество оптимизационных алгоритмов, которые можно использовать для решения проблемы (13). Результаты, представленные в этой статье, были получены путем реализации генетического алгоритма в среде Matlab.

Расчет энергии

Изменение энергии, запасенной в суперконденсаторе, зависит от мощности, подаваемой на конденсатор в единицу времени, и может быть описано следующим образом

Выражая мощность, подаваемую на конденсатор, как произведение тока и напряжения на выводах конденсатора, изменение энергии в данный момент времени t можно выразить как

Полная энергия за промежуток времени [ t ₁ , t ₂ ] можно получить, интегрировав изменения энергии за это время

Учет уравнения. (7), общий запас энергии можно определить как

Предполагая t ₁ =0 и \ (E_ {t_ {1}} =0 \), полная энергия, запасенная в суперконденсаторе в течение временного интервала [0, t ] есть

Обратите внимание, что для α =1 Ур. (18) сводится к классическому

Результаты и обсуждение

Первоначально выполнялась процедура оценки вектора параметров модели суперконденсатора с помощью дробного исчисления. Оценка производилась на основе системы, представленной на рис. 2в, генерирующей на своем входе скачок напряжения или синусоидальную волну. Отклики модели рассчитывались на основе (11). Результаты, полученные с помощью двух процедур идентификации, очень похожи, особенно в случае дробной емкости C _α и дробный порядок α (см. Таблицу 1). Некоторые различия в оценках последовательного сопротивления r _S может быть результатом его зависимости от частоты. Шаговый сигнал состоит из множества высокочастотных гармоник, а синусоидальная волна - только из одной - 0,03 рад / с. Представленные результаты были получены для коммерческого суперконденсатора Samwha Green – Cap EDLC (DB), рассчитанного на 2,7 В с номинальной емкостью 100 Ф и 8 м Ом максимальное эквивалентное последовательное сопротивление ( r _S ) на частоте 1 кГц.

На рисунках 5а и 6а показаны измеренное напряжение суперконденсатора и рассчитанные отклики модели для ступенчатого и синусоидального сигналов соответственно, а на рис. 5b и 6b показывают ошибку ответа модели.

Все полученные результаты показывают высокую согласованность между откликами модели и реальными измерениями, несмотря на то, что были предложены относительно простые модели. Некоторые неточности могут быть связаны с тем, что параметры модели необходимо оценивать в системе заряжаемого и разряжаемого суперконденсатора с использованием источника тока [25]. Кроме того, очень высокие оценки r _P Можно предположить, что это сопротивление можно исключить из модели суперконденсатора, показанной на рис. 2c. Эти очень высокие оценки и их большие расхождения для разных входов указывают на то, что тестовые сигналы, используемые для оценки этого параметра, не соответствуют требованиям. Модель (10) использовалась как наиболее общая форма. Однако для точного определения всех его параметров потребовалось использование других процедур и тестовых сигналов. Значение r _P характеризует ток утечки I _L и должна определяться по сигналу постоянного напряжения, но очень долго - порядка нескольких десятков часов.

Хотя основной целью исследования было измерение энергии, различные условия возбуждения в значительной степени влияли на все оценки параметров (см. Таблицу 2). Например, увеличение амплитуды скачка напряжения существенно изменило порядок дробного интегрирования в результате усиления эффекта диффузионных явлений внутри суперконденсатора. Из таблицы 2 также видно, что суперконденсатор достаточно нелинейный. В результате изменения порядка интегрирования также наблюдается изменение дробной емкости. Это также относится к синусоидальному возбуждению. Значения предполагаемых параметров, особенно α и C _α - зависят от амплитуды и частоты (см. Таблицу 3). Для низких частот важно значение амплитуды, в то время как для высоких частот суперконденсатор ведет себя так, как будто его возбуждает постоянное напряжение.

Расчет энергии

На рисунках 7a и 8a показаны измеренные значения напряжения и тока суперконденсатора для конфигурации, представленной на рисунке 4b. Эти значения использовались для расчета полной энергии, запасенной в конденсаторе (помеченном как E ₁ на рис. 7б, 8б) согласно (16). Как и в процессах идентификации параметров, расчеты проводились как для скачка напряжения, так и для синусоидальной волны на входе в систему. Рассчитанная таким образом энергия для каждого момента времени t сравнивали с энергией, рассчитанной на основе напряжения и емкости в соответствии с (19) (обозначены как E ₃ на фиг. 7b и 8b) и энергия, рассчитанная с использованием исчисления дробного порядка (обозначена как E ₂ на фиг. 7б, 8б) согласно (18). Для уравнения. (19) была принята номинальная стоимость суперконденсатора ( C _n ), в то время как в (18) использовалось значение, полученное в результате процесса оценки, представленного в таблице 1. На рисунке 7b показаны результаты измерений и расчетов энергии для шага напряжения, а на рисунке 8b показаны те же самые величины для синусоидальной волны. Аналогичные расчеты были выполнены для разных ступеней напряжения и синусоидальных возбуждений. На рис. 9a, b показан пример измеренной и рассчитанной энергии для двух ступеней напряжения 0,5 В и 2,7 В соответственно. На рисунке 10 показаны изменения энергии для синусоидального сигнала с частотой 0,03 рад / сек и различными амплитудами 0,1 / 0,25 / 0,5 и 0,7 В. Видно, что различия в определенных значениях энергии соответствуют различиям в расчетных значениях. дробного порядка α . Чем больше разница от значения - 1, тем больше разница в рассчитанных энергиях.

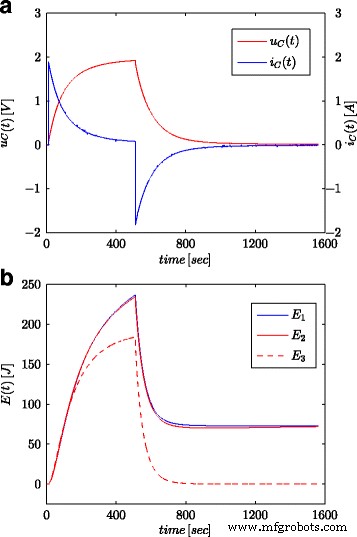
Переходные характеристики для напряжения и тока суперконденсатора ( a ) и расчетные значения энергии ( b )

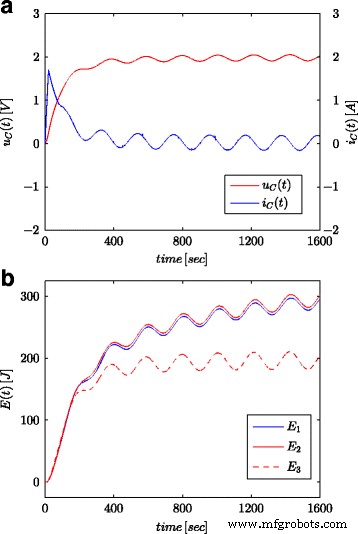
Синусоидальные характеристики напряжения и тока суперконденсатора ( a ) и расчетные значения энергии ( b )

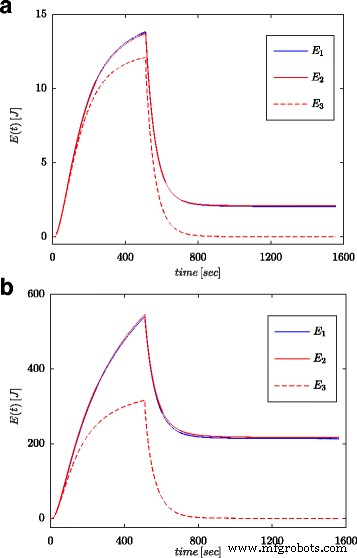
Количество энергии, рассчитанное для ступенчатого возбуждения 0,5 В ( a ) и 2,7 В ( b )

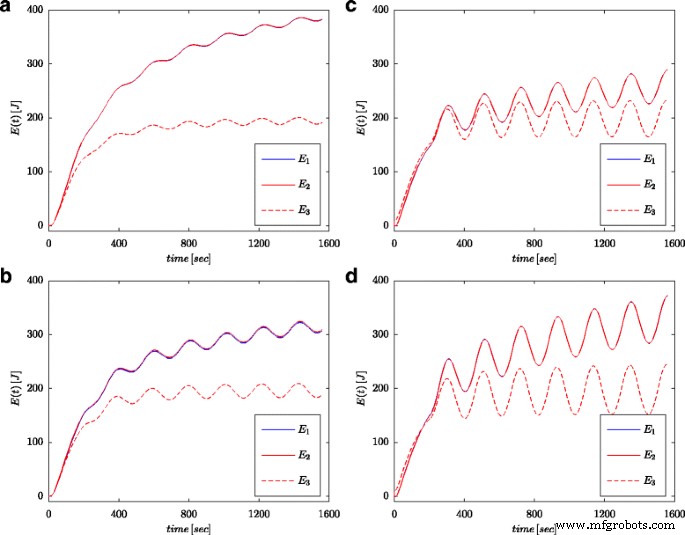
Количество энергии, рассчитанное для синусоидальных возбуждений с частотой 0,03 рад / с и амплитудами 0,1 В ( a ), 0,25 В ( b ), 0,5 В ( c ) и 0,7 В ( d )

Обсуждение

Использование электродов из пористого материала в суперконденсаторах в виде активированного угля, изолированного очень тонким сепаратором, и использование механизмов накопления заряда в виде так называемого двойного слоя, дает огромное увеличение их емкости. Однако применение новых материалов и новых конструктивных решений приводит к тому, что традиционные математические вычисления в виде производных и интегралов целого порядка оказываются неточными. Проведенные измерения и расчеты подтверждают фракционный характер суперконденсаторов. Путем правильной оценки нецелого порядка α производной / интеграла, можно точно смоделировать явления и процессы, происходящие внутри суперконденсатора, используя простые математические модели.

Принимая во внимание реальное значение накопленной энергии, определяемое формулой (16), модель целого порядка с номинальными параметрами (19) занижает количество энергии, в то время как дробная модель (18) показывает почти такое же значение.

Проведенные испытания и измерения были связаны с зарядкой и разрядкой суперконденсатора от источника напряжения. В промышленных условиях суперконденсаторы обычно заряжаются и разряжаются от источников тока. Это может изменить природу системы, поскольку конденсатор больше не является инерциальной системой, а становится типичной интегрирующей. Однако проведенные автором измерения также указывают на наличие диффузионных процессов в таких случаях. В любом случае полезность производной / интеграла Грюндвальда – Летникова здесь подтверждается. Другая проблема связана с реализацией оператора дифференцирования-интеграла GL в виде, например, конечной или усеченной разности GL (6), что может быть обременительным с вычислительной точки зрения. В будущих исследованиях мы сравним аппроксиматоры Oustaloup [35] и FFLD [24, 36, 37], чтобы эффективно решить проблему реализации.

Количество накопленной энергии в суперконденсаторе рассчитывается только на основе измеренного значения напряжения на выводах суперконденсатора и с использованием модели (19) не подходит. Модель (19) действительна только в том случае, если ток конденсатора характеризуется производной целочисленного порядка напряжения конденсатора ( i _C ( т ) =d u _C ( т ) / d t ). Это не относится к суперконденсатору из-за его конструкции и использования специальных материалов. Однако та же проблема возникает с очень большими суперконденсаторами, заряжаемыми от источника тока. Есть и совсем новый элемент в виде супер-аккумуляторов. Во всех этих приложениях изменения тока не характеризуются производной целочисленного порядка напряжения на клеммах как следствие специфических свойств этих элементов.

Выводы

В этой статье представлен новый подход к оценке количества энергии, накопленной в суперконденсаторах. Анализ был проведен с использованием некоторых уникальных свойств моделей дробного порядка. Было показано, что применение такого сложного моделирования приводит к очень точным результатам, которые могут быть получены, даже если сами модели не имеют высокой сложности. Это связано с естественной способностью динамики нецелого порядка моделировать процессы диффузии, точно так же, как перераспределение заряда в суперконденсаторах. Результаты этой статьи подтвердили дробную природу суперконденсаторов.