Электронная структура, зависящая от спина и долины в силицене при периодических потенциалах

Фон

Двумерные (2D) дираковские материалы с гексагональной структурой решетки широко исследуются с момента открытия графена, такого как силицен [1, 2], дихалькогениды переходных металлов [3, 4] и фосфорен [5]. Хотя графен обладает множеством особых свойств, его применение ограничено нулевой шириной запрещенной зоны и слабым спин-орбитальным взаимодействием (SOI). Недавно кремниевый аналог графена, силицен, был получен путем эпитаксиального роста [6–10], и его стабильность была предсказана теоретическими исследованиями [11, 12]. Графен и силицен имеют схожую полосовую структуру около K и K ^′ долины, и их низкоэнергетические спектры описываются релятивистским уравнением Дирака [13]. В отличие от графена, силицен имеет сильную внутреннюю КНИ и изогнутую структуру. Сильный КНИ может открыть брешь в точках Дирака [13, 14] и привести к связи между спиновыми и долинными степенями свободы. Выпученная структура позволяет управлять шириной запрещенной зоны с помощью внешнего электрического поля, перпендикулярного листу силицена [14–16]. Кроме того, силицен имеет то преимущество, что он более совместим с существующей электронной технологией на основе кремния. Эти характеристики делают силицен отличным материалом для наноэлектроники следующего поколения. В частности, силиценовый полевой транзистор при комнатной температуре был успешно изготовлен с помощью процесса выращивания-переноса в эксперименте [17].

Открытие двумерных дираковских материалов открывает новые возможности для изучения квантового управления долиной. Две неэквивалентные долины K и K ^′ в первой зоне Бриллюэна может рассматриваться как дополнительная степень свободы помимо заряда и спина для квантовой информации и квантовых вычислений [18–20]. Например, степень свободы долины может быть включена для расширения спинового кубита электрона до кубита спиновой долины [18]. Поэтому долотроника, которая нацелена на генерацию, обнаружение и управление псевдоспином долины, вызвала значительный интерес. В графене были предложены различные схемы для достижения поляризации долины с использованием уникальных краевых мод [21, 22], эффекта тригонального коробления [23], топологических линейных дефектов [24, 25], деформации [26, 27] и электростатических затворов. [28]. По сравнению с графеном, силицен имеет значительное преимущество при изучении псевдоспина долины. Обнаружено, что силицен проявляет большое разнообразие топологических фаз и чисел Черна при модуляции различных внешних полей [13, 16, 29, 30]. В присутствии электрического поля E _z и поле обмена h , Эзава исследовал фазовую диаграмму в E _z - h плоскость, которая характеризуется индексами спина и долины [16]. Далее, рассматривая КНИ Рашбы, в силицене предсказывается долинно-поляризованное квантовое аномальное холловское состояние из-за топологического фазового перехода [31]. На основе перехода между состояниями предложен спиновый фильтр на основе силицена с почти 100% -ной спиновой поляризацией, устойчивый к слабому беспорядку [32]. Йокояма изучил баллистический перенос через ферромагнитный (FM) силиценовый переход и продемонстрировал контролируемый спин и поляризованный ток долины [33]. В дихалькогенидах переходных металлов с нарушенной инверсионной симметрией спиновое расщепление валентных зон, возникающее из-за собственного КНИ, противоположно в двух долинах из-за симметрии относительно обращения времени [3, 34, 35]. Нарушенная инверсионная симметрия может привести к правилу оптического отбора, зависящему от долины, которое можно использовать для избирательного возбуждения носителей в K или K ^′ долина через правый или левый циркулярно поляризованный свет соответственно [3, 34]. В эксперименте сигнал поляризации долины исследовался с помощью оптических [36, 37] и транспортных [38, 39] измерений. Гигантский эффект Холла нелокальной долины наблюдался в двухслойном графене, подвергающемся воздействию электрического поля затвора, нарушающего симметрию, и нелокальный сигнал сохраняется до комнатной температуры [38]. Недавний обзор долитроники в 2D-материалах Дирака представлен в работе. [40].

Сверхрешетка - это эффективный метод создания электронной структуры в полупроводниках и 2D-материалах [41]. Структуры сверхрешетки с наноразмером могут естественным образом возникнуть в эксперименте, когда графен или силицен помещают поверх металлических подложек [42, 43]. Сверхрешетка в графене может привести к перенормировке анизотропной скорости Ферми [44] и появлению новых дираковских точек в спектре [45–47] из-за киральной природы, которые наблюдались экспериментально [43, 48, 49]. В сверхрешетках силицена с электрическим полем E _z и поле обмена h , снимаются и спиновые, и долинные вырождения. Подтверждено, что структура минизоны и минищели, обусловленные сверхрешетками, зависят от индексов спина и долины [50]. Кроме того, спиновая и долинная поляризации могут быть усилены силиценовыми сверхрешетками [51]. Как и в случае с графеном, в силиценовых сверхрешетках ожидается много новых электронных структур. Однако работ по сверхрешеткам силицена очень мало [50, 51]. В этой статье мы подробно обсуждаем дополнительный аспект, а именно, зонную структуру, зависящую от спина и долины, и транспортные свойства силицена. Мы обнаружили, что индексы спина и долины по-разному влияют на дополнительные точки Дирака и анизотропную скорость, которые можно настраивать с помощью структурных параметров. Скорость сильно подавляется из-за электрического поля и обменного поля. Достигнута замечательная спиновая и долинная поляризация, которая может быть значительно усилена беспорядком.

Работа организована следующим образом. В разделе «Методы» мы представляем теоретический формализм и дисперсионное соотношение. Численные результаты по зонной структуре, спиновой и долинно-поляризованной передаче показаны в разделе «Результаты и обсуждения». В заключение мы подводим итоги в разделе «Выводы».

Методы

В одночастичном приближении электронная структура силицена в окрестности точек Дирака подчиняется эффективному гамильтониану Дирака. Рассматриваемая система представляет собой одномерную сверхрешетку силицена, образованную серией локальных потенциальных барьеров U , поменяйте поля h , и перпендикулярное электрическое поле E _z . U , h , и E _z присутствуют только в областях барьера с шириной барьера d _б , тогда как U = h = E _z =0 в областях ямы с шириной ямы d _w , как показано на рис. 1. Сверхрешетка типа Кронига-Пенни изменяется только вдоль x направление, а длина одной единицы составляет d = d _б + d _w . Подобная модель обсуждалась в [1,2]. [51, 52], в которых основное внимание уделяется термоэлектрическому и электронному транспорту, а не зонной структуре и эффекту беспорядка, исследованным в данной работе. Экспериментально U может быть изготовлен металлическими воротами и h может быть вызван эффектом магнитной близости с FM-изоляторами EuO [33], которые периодически осаждаются поверх слоя силицена (см. рис. 1). Электрическое поле E _z приложенный перпендикулярно к силицену, может вызвать ступенчатый подрешеточный потенциал Δ _z = ℓ E _z , с 2 ℓ ≈0,46Å вертикальное разделение A и B узлов двух подрешеток из-за выпученной структуры [16]. Следовательно, электронные состояния можно описать гамильтонианом

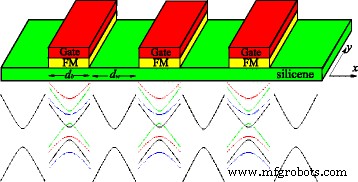
Вверху:схематическое изображение сверхрешеток силицена. FM-изоляторы, такие как EuO и EuS, на поверхности силицена индуцируют обменные поля в силицене, как это было предложено для графена [53]. Металлические вентили наверху FM-изоляторов локально контролируют уровень Ферми. Внизу:схема энергетического спектра в силицене с внешними полями и без них

Δ _{η σ} = Δ _z - η σ λ _ТАК описывает ширину запрещенной зоны для различных индексов спина и долины, которой можно управлять с помощью разнесенного потенциала Δ _z и SOI λ _ТАК . U _σ = U - σ h - эффективный потенциал для различных спиновых индексов. η =± 1 обозначает K и K ^′ долины. σ =± 1 обозначает состояния со спином вверх и вниз. v _F - скорость Ферми. В силицене внутренние и внешние эффекты Рашбы очень малы, и ими можно пренебречь [15].

Из-за трансляционной инвариантности вдоль y направление, поперечный волновой вектор k _y сохраняется. Волновая функция для долины η и вращаем σ в каждом регионе имеет вид Ψ ( x , y ) = ψ ( x ) е ^iky _y с

В областях барьера ε _{η σ} = ε _б =( E - U _σ ) + Δ _{η σ} и x составляющая волнового вектора \ (q _ {\ eta \ sigma} =q_ {b} =\ sqrt {(E - U _ {\ sigma}) ^ {2} - \ Delta ^ {2} _ {\ eta \ sigma} - (\ hbar v_ {F} k_ {y}) ^ {2}} / \ hbar v_ {F} \). В областях скважин ε _{η σ} = ε _w = E - η σ λ _ТАК и \ (q _ {\ eta \ sigma} =q_ {w} =\ sqrt {E ^ {2} - \ lambda _ {SO} ^ {2} - (\ hbar v_ {F} k_ {y}) ^ { 2}} / \ hbar v_ {F} \). к _± = q _{η σ} ± я η к _y . Вероятность передачи T _{η σ} могут быть рассчитаны с использованием метода матрицы переноса. Нормализованная проводимость для конкретного спина в конкретной долине при нулевой температуре определяется как

где θ угол падения относительно x направление. Проводимость с разрешением по спину и долине определяется как \ (G _ {\ uparrow (\ downarrow)} =\ left (G_ {K \ uparrow (\ downarrow)} + G_ {K ^ {\ prime} \ uparrow (\ downarrow) )} \ right) / 2 \) и \ (G_ {K (K ^ {\ prime})} =\ left (G_ {K (K ^ {\ prime}) \ uparrow} + G_ {K (K ^ { \ prime}) \ downarrow} \ right) / 2 \) соответственно. Затем мы вводим спиновую поляризацию P _s и поляризация долины P _v :

На основании теоремы Блоха и условия непрерывности волновых функций дисперсионное соотношение E ( к _x ) для электронов со спином вверх и вниз вблизи K и K ^′ долины можно вычислить,

и k _x - волновое число Блоха. Для упрощения расчета введены безразмерные единицы:\ (E \ rightarrow E d / \ hbar v_ {F} \), \ (U \ rightarrow U d / \ hbar v_ {F} \), \ (\ лямбда _ {SO} \ rightarrow \ lambda _ {SO} d / \ hbar v_ {F} \), \ (\ Delta _ {z} \ rightarrow \ Delta _ {z} d / \ hbar v_ {F} \) , \ (h \ rightarrow hd / \ hbar v_ {F} \), k _y → к _y г , k _x → к _x г , d _w → г _w / d , и d _б → г _б / d . Обратите внимание, что при Δ _z = λ _ТАК = h =0, уравнение. Уравнение (6) сводится к уравнению, найденному для бесщелевого графена в периодическом потенциале, где и спин, и долина вырождены [44–47]. Из уравнения. (6) мы видим, что поле обмена h одна только может вызвать расщепление вращения, в то время как долина сохраняет вырождение. Однако вырождение долины может быть снято электрическим полем E _z с помощью SOI λ _ТАК . Таким образом, комбинация обменного поля и электрического поля могла бы снять вырождение спина и долин [16, 31–33], как показано на рис. 1. В предлагаемой системе электроны с разными спинами вблизи разных долин будут представлять различные зоны конструкции и транспортные средства.

Результаты и обсуждения

В этом разделе мы будем использовать приведенные выше уравнения для расчета зонной структуры и транспортных свойств для различных индексов спина и долины в сверхрешетках силицена. В дальнейшем предполагается, что ширина барьеров и колодцев одинакова. Результаты для случая с неравной шириной колодца и барьера ( d _б ≠ г _w ) аналогичны таковым в бесщелевом графене [47]. Некоторые параметры установлены как d _б = d _w =50 нм и λ _ТАК =3,9 мэВ в силицене, если не указано иное. Мы сконцентрируемся на первых двух мини-зонах (мини-зоны с самой низкой валентностью и проводимостью) вблизи уровня Ферми.

Структура диапазона, зависящая от вращения и долины

Во-первых, влияние потенциала U на мини-зонах изображено на рис. 2. Для одновременного обсуждения щелевого и бесщелевого энергетических зон мы положили Δ _z =7,8 мэВ =2 λ _ТАК . При отсутствии потенциала ( U =0), электрон со спином вверх около K долина ( K ↑ электрон) и электрон со спином вниз около K ^′ долина ( K ^′ ↓ электрон) являются бесщелевыми (см. рис. 2 (a1, a4)), а электрон со спином вниз вблизи K долина ( K ↓ электрон) и электрон со спином вверх около K ^′ долина ( K ^′ ↑ электрон) имеют большую щель (см. рис.2 (а2, а3)). Мини-зоны электронов со вращением вверх (или вниз) сдвигаются в область отрицательной (или положительной) энергии от E =0 по h , за счет эффективного потенциала U _σ = U - σ h . Ленточные структуры K ↑ (или K ↓ ) электрон и K ^′ ↓ (или K ^′ ↑ ) электрон имеет зеркальную симметрию относительно E =0, что согласуется с формулой. (6). Однако эта зеркальная симметрия нарушается в присутствии U . Очевидно, как U увеличивается, появляются дополнительные точки Дирака, количество которых тем временем увеличивается. Лишние точки Дирака могут быть продемонстрированы хиральностью волновых функций в их окрестности [46]. Характеристики точек Дирака в системе силицен в значительной степени зависят от степеней свободы спина и долины, как показано на рис. 2. Например, в U =135 мэВ на рис. 2 (d1 – d4) для K ↑ , К ↓ , К ^′ ↑ и K ^′ ↓ электронов число точек Дирака равно 5, 6, 4 и 7 соответственно. Для конкретных значений U , например U =40,66 мэВ для K ↓ электрон (см. рис. 2 (b2)) и U =100,63 мэВ для K ^′ ↑ электрона (см. рис. 2 (c3)), новая точка Дирака может быть сгенерирована при k _y =0, и он разделится на пару, которые движутся в противоположных направлениях от k _y =0 баллов, но всегда сохраняется k _x =0, как U далее увеличивается. Как следствие, ширина запрещенной зоны для K ↓ и K ^′ ↑ электроны замыкаются (см. рис. 2 (b2, c3)), и система с зазором становится бесщелевой. Чтобы найти критическое значение U , мы устанавливаем d _б = d _w и k _x =0. Аналогично правилу в бесщелевом графене [47], принимая во внимание теорему о неявной функции, можно сделать вывод, что продольные волновые векторы в новых точках Дирака удовлетворяют q _б = q _w когда

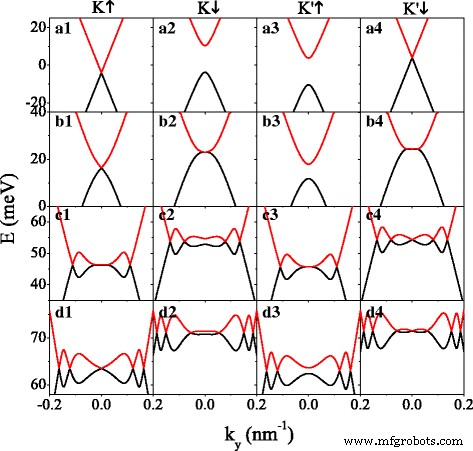
Энергетический спектр в зависимости от k _y для нескольких разных значений потенциала U . (a1 – a4) U =0; (b1 – b4) U =40,66 мэВ; (c1 – c4) U =100,63 мэВ; (d1 – d4) U =135,0 мэВ. Значения параметров: h =8,0 мэВ, Δ _z =7,8 мэВ и k _x =0

Для K ↑ и K ^′ ↓ электроны с η σ =1, когда Δ _z =2 λ _ТАК , Уравнение (7) можно уменьшить до

Соответственно, уравнение. (6) превращается в

что выполняется, когда \ (\ left (\ epsilon _ {b} ^ {2} + \ epsilon _ {w} ^ {2} \ right) q_ {w} ^ {2} + (\ epsilon _ {b} - \ epsilon _ {w}) ^ {2} k ^ {2} _ {y} =-2 \ epsilon _ {w} \ epsilon _ {b} q_ {w} ^ {2} \) или q _w г =2 n π ( нет является положительным целым числом). На основании уравнения. (8) имеем ε _б =- ε _w , поэтому первое равенство выполняется, только если k _{y 0} =0 для K ↑ и K ^′ ↓ электроны на Δ _z =2 λ _ТАК , соответствующая исходной точке Дирака. Решения q _w г =2 n π иметь форму

Когда \ (\ sqrt {E_ {0} ^ {2} - \ lambda _ {SO} ^ {2}} d / 2 \ pi \ hbar v_ {F} \ geq n \), k _{y 0} реально, и возникнут новые точки Дирака, которые точно расположены в ( E ₀ , k _{y 0} ). При низких значениях U , k _{y 0} мнимо, и решения для n нет , что означает отсутствие лишних точек Дирака. Точки Дирака появляются только после критического значения U , например U =40,66 мэВ для K ↓ электронов на рис. 2 (b2), соответствующих n =1. Согласно формуле. (10), Число точек Дирака N _Д может быть получен. Когда Δ _z =2 λ _ТАК ,

для K ↑ и K ^′ ↓ электроны, а

для K ↓ и K ^′ ↑ электроны, где [...] обозначает целую часть. Обратите внимание, что при критическом значении U , например U =40,66 мэВ и 100,63 мэВ, количество точек Дирака N _Д =2 n −1 для K ↓ и K ^′ ↑ электронов (см. рис. 2 (b2, c3)).

Уравнения (7) и (10) показывают, что положения и количество точек Дирака можно регулировать электрическим полем E _z и поле обмена h . На рисунке 3 показано количество точек Дирака N . _Д как функция от U для разных значений E _z и h . Когда Δ _z =7,8 мэВ на рис. 3а, при увеличении U , N _Д для K ↑ и K ^′ ↓ электронов увеличивается в виде нечетного числа, в соответствии с формулой. (11). N _Д для K ↓ и K ^′ ↑ электронов увеличивается в виде четного числа, в соответствии с формулой. (12), кроме N _Д при критическом значении. Сравнение между рис. 3a и b показывает, что как h увеличивается, критическое значение для электрона со спином вниз (или вверх) постепенно уменьшается (или увеличивается). Когда Δ _z =15 мэВ ≠ 2 λ _ТАК на рис. 3c, N _Д для всех электронов увеличивается в виде четного числа, кроме N _Д при критическом значении. В частности, критические значения U различны для электрона с разными спинами и долинами. Точки Дирака можно контролировать путем совместной модуляции параметров U , E _z , и h .

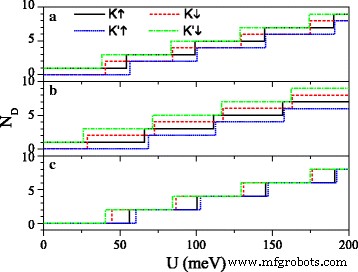
Количество точек Дирака N _Д против потенциала U . ( а ) h =8,0 мэВ и Δ _z =7,8 мэВ; ( б ) h =20,0 мэВ и Δ _z =7,8 мэВ; ( c ) h =8,0 мэВ и Δ _z =15,0 мэВ

Потенциал U и ширина барьера d _б может использоваться для регулирования ширины запрещенной зоны, как показано на рис. 4. Зазоры для K ↑ и K ^′ ↓ электроны малы, а промежутки для K ↓ и K ^′ ↑ электроны большие из-за Δ _{η σ} = Δ _z - η σ λ _ТАК . Как U увеличивается, все минизоны постепенно перемещаются в сторону области высоких энергий (см. рис. 4a), и все запрещенные зоны демонстрируют затухающие колебания с U (см. рис. 4б). Когда U = σ h , эффективный потенциал равен нулю, а зазор достигает максимального значения. Разрыв закрывается при критическом значении U , за счет появления новых точек Дирака. На рис. 4c, d изображена зависимость минизон и запрещенных зон от ширины барьера d _б в U =0. В отсутствие внешнего поля ( d _б =0) минизоны остаются вырожденными, а щель на уровне Ферми составляет 2 λ _ТАК . С появлением d _б , мини-зона расщепляется, при этом долина и спин становятся невырожденными. Мини-зоны K ↑ (или K ↓ ) и K ^′ ↓ (или K ^′ ↑ ) электроны сохраняют зеркальную симметрию относительно E =0 (см. Рис. 4в). Как d _б увеличивается, зазоры K ↓ и K ^′ ↑ электроны расширяются постепенно. Разрывы K ↑ и K ^′ ↓ электроны уменьшаются до нуля, когда d _б удовлетворяет d _б / d _w = λ _ТАК / Δ _z , а затем увеличивайте на d _б (см. рис. 4d). Ширина зазора приближается к насыщению с дальнейшим увеличением d _б . Кроме того, ширина мини-зоны сужается как d _б увеличивается (не показано на рисунке) из-за меньшей связи собственных состояний. Влияние электрического поля на ширину запрещенной зоны аналогично тому, что было в предыдущем исследовании [50].

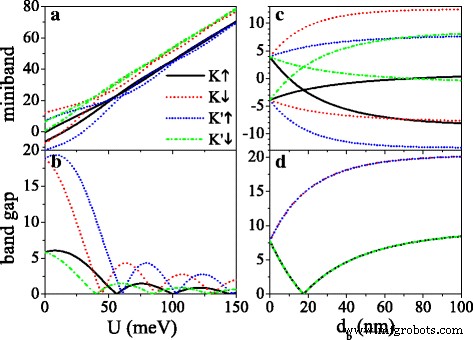
( а ) Минизоны около уровня Ферми и ( b ) их ширины запрещенной зоны в исходной точке Дирака в зависимости от потенциала U , в d _б = d _w =50 нм. ( c ) Минизоны около уровня Ферми и ( d ) их ширины запрещенной зоны в исходной точке Дирака по сравнению с d _б , в U =0 и d _w =50 нм. Значения остальных параметров: h =8,0 мэВ, Δ _z =15,0 мэВ и k _x = k _y =0

Групповая скорость сильно зависит от индексов спина и долины, как показано на рис. 5. Компоненты ( v _x , v _y ) скорости можно определить как

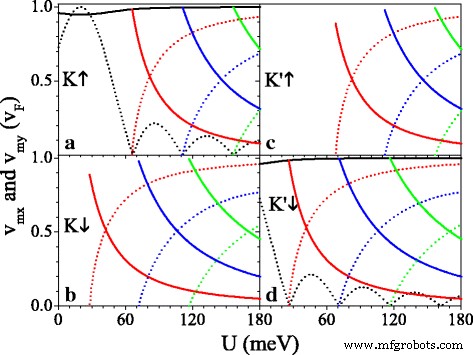
( а - г ) Скорость в зависимости от потенциала U , а параметры установлены как h =20,0 мэВ и Δ _z =7,8 мэВ. Сплошные черные, красные, синие и зеленые кривые - скорости v _{0 x} , v _{1 x} , v _{2 x} , и v _{3 x} , соответственно. Черные, красные, синие и зеленые пунктирные кривые - скорости v _{0 г} , v _{1 г} , v _{2 г} , и v _{3 г} соответственно

На рисунке 5 представлены компоненты скорости v . _mx и v _мой в единицах v _F в исходной точке Дирака ( м =0) и новые точки Дирака ( m =1,2,3). Это видно как U увеличивается, v _{0 г} колеблется затухающим образом и v _{0 x} ≈ v _F практически не изменяется (см. рис. 5а, г). При критическом значении U где появляются новые точки Дирака, v _mx ≈ v _F но v _{0 г} = v _мой =0, что указывает на коллимационное поведение вдоль k _x направление для конкретных спинов и долин. Когда U превышает критическое значение и далее увеличивается, v _мой увеличить до v _F но v _mx постепенно уменьшаются до нуля. Эффект периодического потенциала сильно анизотропен из-за хиральной природы. Особенности анизотропии скорости различны для разных спинов и впадин из-за зазора Δ _{η σ} и потенциал U _σ , которым можно управлять, используя U . Принимая U =20 мэВ, например, v _{0 г} = v _F для K ↑ электрон намного больше, чем v _{0 г} =0,16 v _F для K ^′ ↓ электрон, а не v _{0 г} для K ↓ и K ^′ ↑ электроны из-за запрещенной зоны. v _mx (или v _мой ) для электрона со спином вверх всегда больше (или меньше), чем для электрона со спином вниз в той же долине. Примечательно, что рис. 5 также подразумевает, что для небольшого значения U , v _{0 x} , v _{0 г} , и v _mx меньше v _F из-за Δ _z и h , кроме бесщелевой системы [44]. Например, v _{1 x} =0,98 v _F , 0,89 v _F , 0,89 v _F и 0,98 v _F для K ↑ , К ↓ , К ^′ ↑ и K ^′ ↓ электронов соответственно при появлении точки Дирака. Чтобы осветить влияние Δ _z и h от групповой скорости, на рис. 6 показаны скорости ( v _{0 x} , v _{0 г} ) как функция (а) Δ _z и (б) h для K ↑ электрон. Из рис. 6а ясно видно, что v _{0 x} монотонно убывает с Δ _z а v _{0 г} нечувствителен к изменению Δ _z . Напротив, v _{0 x} десенсибилизируется к h , а v _{0 г} увеличивается до максимального значения v _{0 г} = v _F в h = σ U а затем уменьшается на h . Результаты показывают, что групповая скорость может быть подавлена ​​с помощью Δ _z и h в силицене.

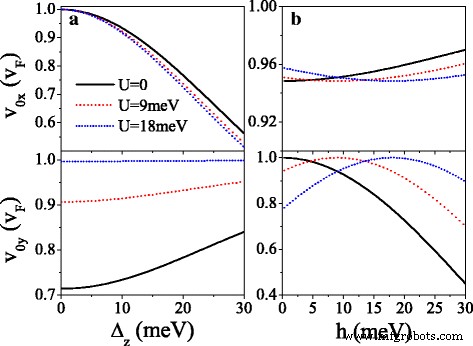
Скорости v _{0 x} и v _{0 г} по сравнению с ( a ) Δ _z и ( b ) h , для K ↑ электрон. ( а ) h =20,0 мэВ и λ _ТАК = Δ _z / 2. ( б ) Δ _z =7,8 мэВ

Транспорт, поляризованный по спинам и долинам

Структура полос, зависящая от вращения и впадины, отражается на свойствах переноса и обеспечивает руководство в управлении переносом. В этом разделе мы обсуждаем свойства спин- и долинно-поляризованного переноса через конечную сверхрешетку силицена. На рисунке 7 показана вероятность передачи T _{η σ} для (a, c) K ↑ и (b, d) K ↓ электронов, а номер периода n =10. Красные пунктирные кривые - это мини-зоны, которые также являются границами для различных электронных состояний, определяющих передачу. Мы можем видеть, что передача ограничена в области минизоны и отсутствует передача в области запрещенной зоны (см. Рис. 7a, b). Распределение передачи симметрично относительно k _y =0 из-за симметричных минизон. Резонансная характеристика передачи возникает из резонансных состояний. Следует отметить, что передача все еще существует в области промежутка около k _y =0 из-за туннельного эффекта собственных состояний. Т _{η σ} на уровне Ферми для K ↑ и K ↓ электроны показаны на рис. 7в, г) соответственно. Хорошо видно, что много тонких резонансных пиков с T _{η σ} =1 встречаются точно в положениях точек Дирака, что предполагает применение системы в качестве фильтра спина и впадины.

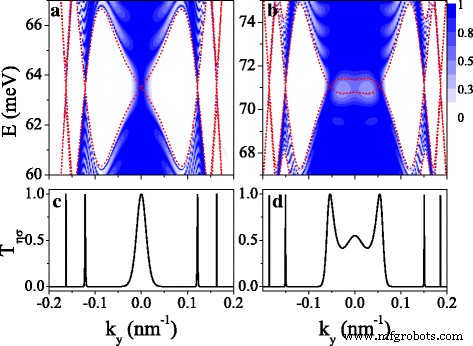
Контурная передача Т _{η σ} ( E , k _y ) для ( a ), ( c ) К ↑ электрон и ( b ), ( d ) К ↓ электрон. Значения параметров такие же, как на рис. 2 (d1 – d4), и n =10

Сильная зависимость зонной структуры от индексов спина и долины способствует реализации высоких спиновых и долинных поляризаций. На рисунке 8 представлены минизоны, проводимость G _{η σ} , спиновая поляризация P _s , и поляризация долины P _v как функция потенциала U . It can be found that the distribution of conductance is completely in agreement with the band structure, that is, the conductance (or conductance gap) corresponds to the miniband (or band gap). The minibands for spin-up and spin-down electrons could be alternative distribution by adjusting h правильно. Consequently, \(G_{K(K^{\prime })\uparrow }\) and \(G_{K(K^{\prime })\downarrow }\) present alternative distribution as well, i.e., \(G_{K(K^{\prime })\uparrow }\) nearly vanishes for those regions where \(G_{K(K^{\prime })\downarrow }\) is in resonance and vice versa. This result directly leads to a remarkable spin polarization, proposing a switching effect of spin polarization (see Fig. 8a). By changing Δ _z , the minibands and conductances for electrons near K and K ^′ valleys could be controlled, leading to a fully valley-polarized current (see Fig. 8b). Compared with spin polarization, the valley polarization is not perfect enough. However, this drawback could be remedied via the disorder structure of the system, as discussed in the following.

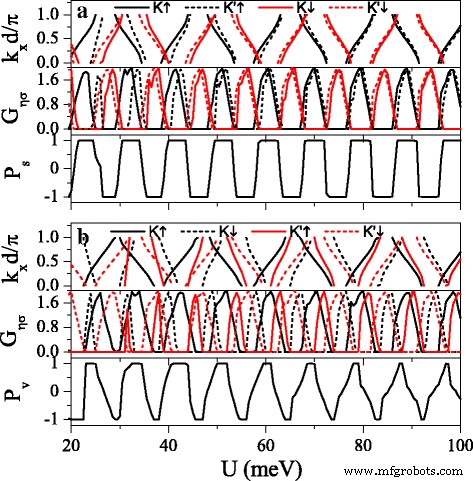
Minibands, conductances G _{η σ} , spin polarization P _s , and valley polarization P _v versus potential U . ( а ) Δ _z =4.0 meV. ( б ) Δ _z =12.0 meV. Other parameters are set as h =7.0 meV, E =6.0 meV, d _б =d _w =120 nm, and n =10

Figure 9 shows the (a) spin polarization P _s and (b) valley polarization P _v in (U ,h ) space. Interestingly, both P _s and P _v present periodical changes in the considered region, which is not observed in the ferromagnetic silicene junction [33]. Both distributions of P _s and P _v are antisymmetric with respect to h →−h . It is possible to achieve independently a full spin and valley polarization by a proper tuning of the fields U и h . For example, when h =6 meV and U =42 meV, P _s ≈1 and P _v ≈1, meaning that the current is mainly contributed by K ↑ electrons. When h =6 meV and U =44 meV, P _s ≈1 and P _v ≈−1 while P _s ≈−1 and P _v ≈−1 at h =6 meV and U =46 meV. The results demonstrate that a spin and valley polarization can be switched effectively.

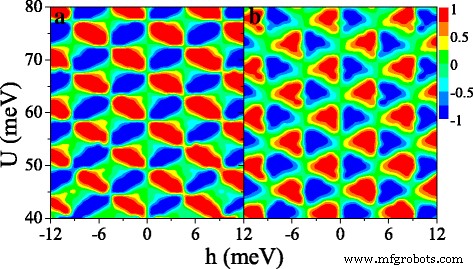
Contour plot of (a ) spin polarization P _s (U ,h ) и ( b ) valley polarization P _v (U ,h ), at Δ _z =10.0 meV. The values of other parameters are the same as these in Fig. 8

In experiment, the structural imperfection of the model is unavoidable due to the limitations of the experimental techniques. Therefore, it is necessary to discuss the effect of the disorder on transmission. When the electric field or exchange field presents disorder, the conductance, spin polarization, and valley polarization are shown in Figs. 10 and 11. We set disorder situations of Δ _z и h fluctuate around their mean values, given by 〈Δ _z 〉=Δ _{z 0} and 〈h 〉=h ₀ , соответственно. The fluctuations are given by

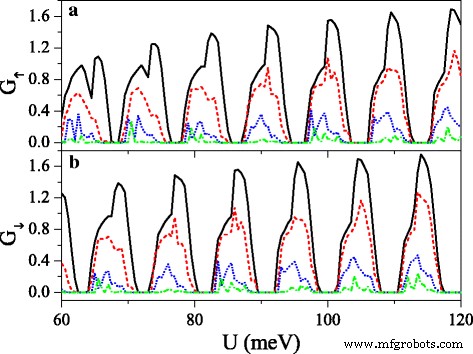
Conductances (a ) G _↑ and (b ) G _↓ versus potential U , when the electric field presents disorder, at n =50 and Δ _{z 0} =20.0 meV. The solid, dashed, dotted, and dash-dotted curves correspond to the disorder strength δ =0.0, 0.1, 0.3, and 0.6, respectively. The values of other parameters are the same as these in Fig. 8

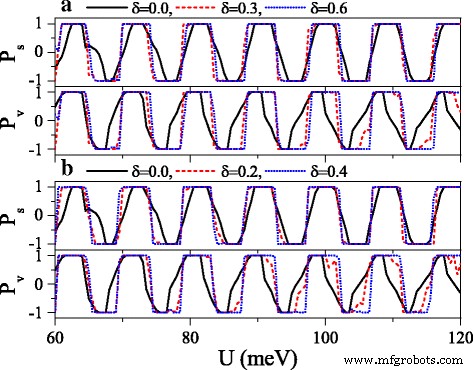
Polarizations P _s and P _v versus potential U when a the electric field or b the exchange field presents disorder. Δ _{z 0} =20.0 meV and h =7.0 meV in (a ). Δ _z =20.0 meV and h ₀ =7.0 meV in (b ). The values of other parameters are the same as these in Fig. 10

where {ζ _я } is a set of uncorrelated random variables or white noise, − 1<ζ _я <1, δ is the disorder strength, and i is the site index. Note that the disorder only takes place in the x direction, and the system is always homogeneous in y направление. Thus, k _y still keeps conservation. Figure 10 exhibits the effect of the disorder of the electric field on the conductances (a) G _↑ and (b) G _↓ . With the presence and increase of the disorder strength δ , both G _↑ and G _↓ are suppressed gradually, and each resonant peak splits into many small peaks. One may find that the conductance range is narrowed while the conductance gap range is broadened. Hence, the allowable (or forbidden) ranges of G _↑ completely fall into the forbidden (or allowable) ranges of G _↓ , giving rise to an excellent spin polarization (see Fig. 11). Furthermore, the positions of conductances and conductance gaps are nearly invariable as δ changes, suggesting that the miniband and band gap are insensitive to the disorder. Note that the disorder effect of the electric field on G _К and G _К ^′ is similar to that observed in Fig. 10. Figure 11 presents the disorder effects of (a) the electric field and (b) the exchange field on polarizations P _s and P _v . Obviously, with the increase of δ , P _s and P _v increase greatly, and the polarization platform is broadened. Thus, a full spin and valley polarization is realized. Comparison between Fig. 11a and b indicates that the disorder effect of exchange field is more prominent. The results demonstrate that the disorder could enhance the spin and valley polarizations compared with the order case, which is an advantage in realistic application.

Выводы

In summary, we demonstrated detailedly that band structure and transport property of silicene under a periodic field strongly depend on the spin and valley degrees of freedom. The numerical results indicate that electrons with different spins and valleys have various characteristics in Dirac point, bang gap, and group velocity. In particular, owing to the electric field and exchange field, the anisotropic velocity is restrained, which displays a collimation behavior for specific spins and valleys. Therefore, the transmission presents strong spin- and valley-dependent feature, consistent with the band structure, resulting in a significant spin and valley polarizations. In addition, the disorder could greatly enhance the spin and valley polarizations. Finally, we hope these results can be conducive to the potential applications of the spin and valley indices.

Сокращения

2D:

Двумерный

FM:

Ferromagnetic

SOI:

Spin-orbit interaction