Карты Карно, таблицы истинности и логические выражения

Кто разработал карту Карно?

Морис Карно, инженер по телекоммуникациям, разработал карту Карно в Bell Labs в 1953 году при разработке схем телефонной коммутации на основе цифровой логики.

Использование карты Карно

Теперь, когда мы разработали карту Карно с помощью диаграмм Венна, давайте применим ее. Карты Карно уменьшить логика работает быстрее и проще по сравнению с булевой алгеброй. Под сокращением мы подразумеваем упрощение, сокращая количество входов и входов.

Нам нравится упрощать логику до наименьшей стоимости форма для экономии затрат за счет исключения компонентов. Мы определяем наименьшую стоимость как наименьшее количество вентилей с наименьшим числом входов на вентиль.

Если у них есть выбор, большинство студентов после изучения этого инструмента выполняют логическое упрощение с помощью карт Карно, а не булевой алгебры.

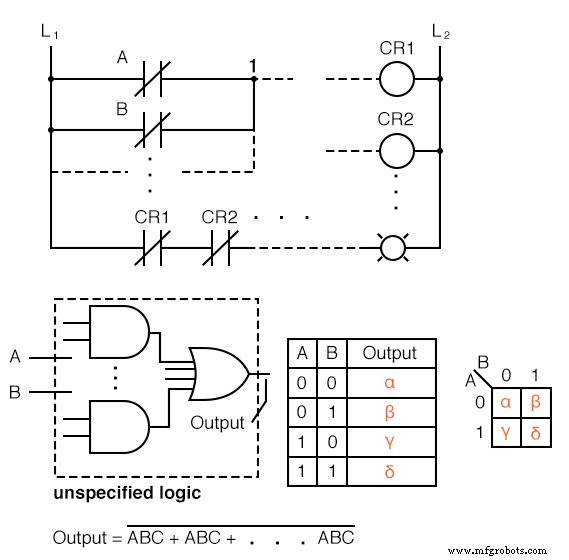
Выше мы показываем пять отдельных элементов, которые представляют собой просто разные способы представления одного и того же:произвольной функции цифровой логики с двумя входами. Сначала идет релейная релейная логика, затем логические вентили, таблица истинности, карта Карно и логическое уравнение.

Дело в том, что все они эквивалентны. Два входа A и B может принимать значения 0 или 1 , высокий или низкий, открытый или закрытый, истина или ложь, в зависимости от обстоятельств. Есть 2 ² =4 комбинации входов, дающих выход. Это применимо ко всем пяти примерам.

Эти четыре выхода можно наблюдать на индикаторе в релейной релейной логике, на логическом щупе на схеме затвора. Эти результаты могут быть записаны в таблице истинности или в карте Карно. Посмотрите на карту Карно как на переставленную таблицу истинности.

Выходные данные булевого уравнения могут быть вычислены по законам булевой алгебры и перенесены в таблицу истинности или карту Карно.

Какое из пяти эквивалентных логических описаний мы должны использовать? Тот, который наиболее полезен для выполнения поставленной задачи.

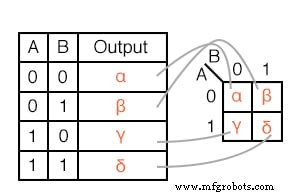
Выходные данные таблицы истинности взаимно однозначно соответствуют записям карты Карно. Начиная с верха таблицы истинности, входные данные A =0, B =0 дают выход α.

Обратите внимание, что этот же выходной α находится в карте Карно по адресу ячейки A =0, B =0, в верхнем левом углу K-карты, где пересекаются строка A =0 и столбец B =0. Другая таблица истинности выводит β, χ, δ из входов AB =01, 10, 11, которые находятся в соответствующих местоположениях K-карты.

Ниже мы показываем смежные области с двумя ячейками на K-карте с двумя переменными с помощью предыдущей прямоугольной диаграммы Венна, как и булевы области.

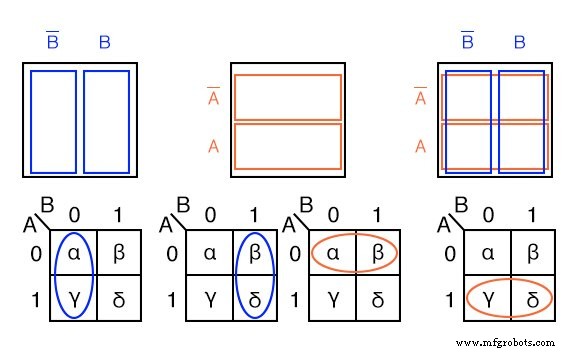
Клетки α и χ смежны в K-отображении как эллипсы в крайнем левом K-отображении ниже. Ссылаясь на предыдущую таблицу истинности, это не так. Между ними есть еще одна запись в таблице истинности (β). Это подводит нас к сути организации K-карты в квадратный массив, ячейки с любыми общими логическими переменными должны быть близко друг к другу, чтобы создать шаблон, который бросается в глаза.

Для ячеек α и χ они имеют логическую переменную B ’. в общем. Мы знаем это, потому что B =0 (то же, что и B ’ ) для столбца над ячейками α и χ. Сравните это с квадратной диаграммой Венна над K-картой.

Аналогичное рассуждение показывает, что β и δ имеют логическое значение B . (B =1) в общем. Тогда α и β имеют логическое значение A ’ (A =0) вместе. Наконец, χ и δ имеют логическое значение A (A =1) вместе. Сравните две последние карты со средней квадратной диаграммой Венна.

Подводя итог, мы ищем общность логических переменных среди ячеек. Карта Карно организована таким образом, чтобы мы могли видеть эту общность. Давайте попробуем несколько примеров.

Примеры

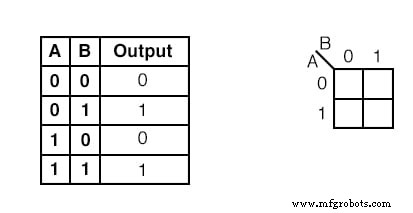
Пример:

Перенесите содержимое таблицы истинности на карту Карно выше.

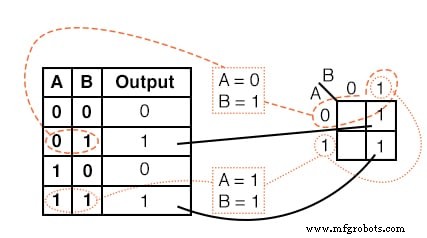
Решение:

Таблица истинности содержит два 1 с. K-карта должна иметь их обоих. найдите первый 1 во 2-й строке таблицы истинности выше.

• обратите внимание на адрес AB таблицы истинности
• найдите ячейку на K-карте с таким же адресом
• поместите 1 в этой ячейке

Повторите процесс для 1 в последней строке таблицы истинности.

Пример:

Для карты Карно в указанной выше задаче напишите логическое выражение. Решение ниже.

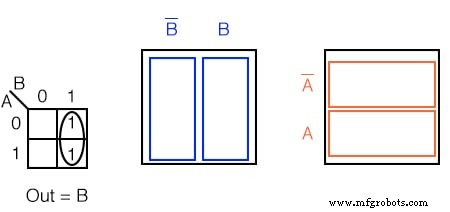
Решение:

Ищите соседние ячейки, то есть выше или сбоку от ячейки. Диагональные клетки не смежные. Соседние ячейки будут иметь одну или несколько общих логических переменных.

• Сгруппируйте (обведите) два 1 s в столбце
• Найдите переменные вверху и / или сбоку, которые совпадают для группы, запишите это как логический результат. Это B в нашем случае.
• Игнорировать переменные, которые не совпадают для группы ячеек. В нашем случае A варьируется, равно 1 и 0, логическое значение A игнорируется.
• Игнорировать любые переменные, не связанные с ячейками, содержащими единицы. B ’ под ним никого нет. Игнорировать B ’
• Результат Out =B

Это может быть легче увидеть, сравнив диаграмму Венна справа, в частности, B столбец.

Пример:

Напишите логическое выражение для карты Карно ниже.

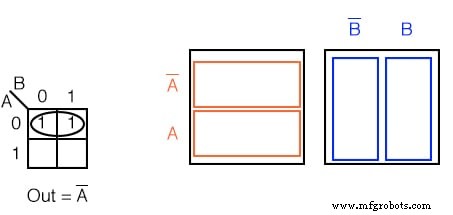
Решение: (вверху)

• Сгруппируйте (обведите) две единицы в ряду
• Найдите переменные, одинаковые для группы, Out =A ’.

Пример:

Для таблицы истинности ниже перенесите выходные данные в Karnaugh, затем напишите логическое выражение для результата.

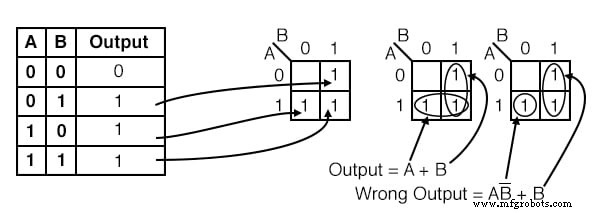
Решение:

Перенести 1 s от местоположений в таблице истинности до соответствующих местоположений на K-карте.

• Сгруппируйте (обведите) две единицы в столбце под B =1 .
• Сгруппируйте (обведите) две единицы в строке справа от A =1 .
• Напишите термин продукта для первой группы = B
• Напишите термин продукта для второй группы = A
• Запишите сумму произведений двух указанных выше терминов Выход =A + B

Решение K-карты посередине является самым простым или самым дешевым решением. Менее желательное решение находится справа. После объединения двух 1 s, мы совершаем ошибку, формируя группу из 1 клетки. Причина, по которой это нежелательно, заключается в следующем:

• В отдельной ячейке содержится термин продукта AB ’.
• Соответствующее решение: Выход =AB ’+ B .
• Это не самое простое решение.

Как забрать этот сингл 1 состоит в том, чтобы сформировать группу из двух человек с помощью 1 справа от него, как показано в нижней строке средней K-карты, хотя эта 1 уже включен в группу столбцов ( B ). Нам разрешено повторно использовать ячейки для формирования больших групп. Фактически, это желательно, потому что это приводит к более простому результату.

Мы должны указать, что любое из вышеперечисленных решений, «Выход» или «Неверный выход», является логически правильным. Обе схемы дают одинаковый выходной сигнал. Дело в том, что первая схема является самым дешевым решением.

Пример:

Заполните карту Карно для логического выражения ниже, затем напишите логическое выражение для результата.

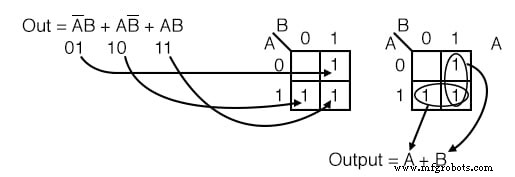
Решение: (вверху)

В логическом выражении есть три продукта. Будет 1 вводится для каждого термина продукта. Хотя в целом количество 1 s на термин продукта зависит от количества переменных в термине продукта по сравнению с размером K-карты.

Термин продукта - это адрес ячейки, в которой находится 1 введен. Первый термин продукта, A’B , соответствует 01 ячейка на карте. А 1 вводится в эту ячейку. Два других P-условия вводятся в сумме, равной трех 1 .

Затем продолжите группировку и извлечение упрощенного результата, как в предыдущей задаче с таблицей истинности.

Пример:

Упростите приведенную ниже логическую схему.

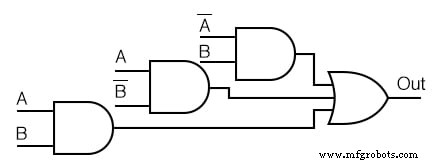
Решение: (Рисунок ниже)

• Напишите логическое выражение для исходной логической схемы, как показано ниже.
• Перенесите условия продукта на карту Карно.
• Формируйте группы ячеек, как в предыдущих примерах.
• Напишите логическое выражение для групп, как в предыдущих примерах.
• Нарисуйте упрощенную логическую схему.

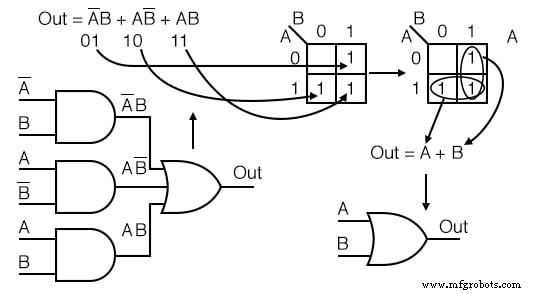
Пример: Упростите приведенную ниже логическую схему.

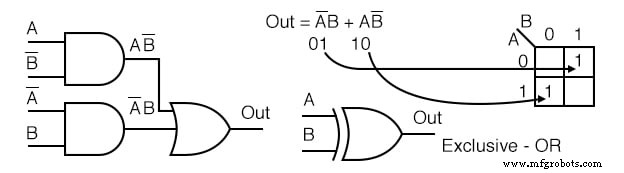
Решение:

• Напишите логическое выражение для исходной логической схемы, показанной выше.
• Перенесите условия продукта на карту Карно.
• Невозможно формировать группы.
• Никакое упрощение невозможно; оставьте как есть.

Для приведенной выше схемы невозможно логическое упрощение. Иногда такое бывает. Ни методы карт Карно, ни булева алгебра не могут еще больше упростить эту логику.

Мы показываем схематический символ «Исключающее ИЛИ» выше; однако это не логическое упрощение. Это просто улучшает вид схематической диаграммы.

Поскольку невозможно упростить логику исключающего ИЛИ и она широко используется, она предоставляется производителями как базовая интегральная схема (7486).

СВЯЗАННЫЕ РАБОЧИЕ ТАБЛИЦЫ:

• Картографический лист Карно
• Рабочий лист булевой алгебры
• Рабочий лист базовой логики