Логические алгебраические тождества

В математике идентичность утверждение истинно для всех возможных значений его переменной или переменных.

Алгебраическое тождество x + 0 =x говорит нам, что что угодно (x) добавлен к нулю равно исходному «все», независимо от того, какое значение это « что-нибудь ”(X) может быть.

Как и обычная алгебра, у булевой алгебры есть свои уникальные тождества, основанные на бивалентных состояниях булевых переменных.

Аддитивные идентичности

Добавление нуля

Первое логическое тождество состоит в том, что сумма всего и ноль то же самое, что и исходное « что угодно . »

Это тождество не отличается от своего алгебраического эквивалента действительных чисел:

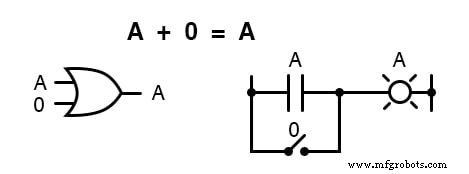
Независимо от значения A , результат всегда будет одинаковым:когда A =1 , вывод также будет 1 ; когда A =0 , вывод также будет 0 .

Добавление одного

Следующая идентичность определенно отличается от любой, встречающейся в нормальной алгебре.

Здесь мы обнаруживаем, что сумма « ничего ”И один это один :

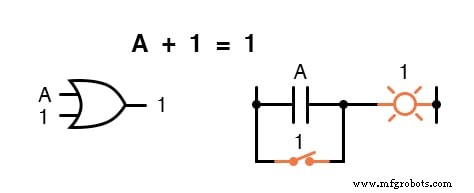
Независимо от того, каково значение A, сумма A и 1 всегда будет равна 1.

В некотором смысле сигнал «1» отменяет влияние A на логическую схему, оставляя выходной сигнал фиксированным на логическом уровне 1.

Добавление количества к самому себе

Затем мы исследуем эффект добавления A и A вместе, что аналогично соединению обоих входов логического элемента ИЛИ друг к другу и активируя их одним и тем же сигналом:

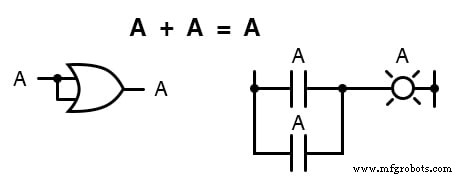
В алгебре действительных чисел сумма двух идентичных переменных в два раза превышает значение исходной переменной (x + x =2 x), но помните, что в мире логической математики нет понятия «2», только 1 и 0, поэтому мы не можем сказать, что A + A =2A .

Таким образом, когда мы прибавляем к себе логическую величину, сумма будет равна исходной величине: 0 + 0 =0 и 1 + 1 =1 .

Добавление количества к своему дополнению

Вводя уникальную логическую концепцию дополнения в аддитивную идентичность, мы обнаруживаем интересный эффект.

Поскольку должен быть один « 1 ”Значение между любой переменной и ее дополнением, и поскольку сумма любой логической величины и 1 равна 1, сумма переменной и ее дополнения должна быть 1:

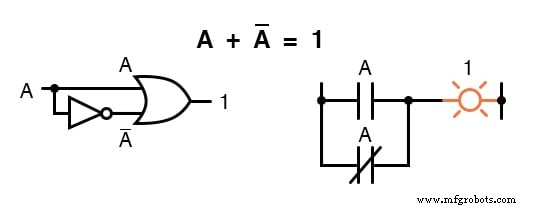
Мультипликативные идентичности

Так же, как есть четыре булевых аддитивных тождества ( A + 0, A + 1, A + A и A + A ’ ), поэтому существует четыре мультипликативных тождества: Ax0, Ax1, AxA и AxA ’ . Из них первые два не отличаются от своих эквивалентных выражений в регулярной алгебре:

Умножение на 0 или 1

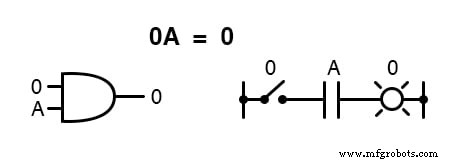
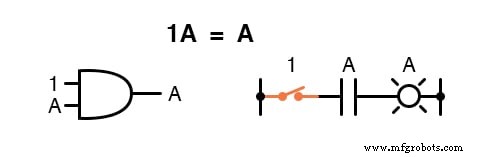
Умножение количества на себя

Третье мультипликативное тождество выражает результат умножения логической величины на себя.

В нормальной алгебре произведение переменной и самого себя представляет собой квадрат этой переменной (3 x 3 =3 ² =9).

Однако концепция квадрата подразумевает количество 2, что не имеет значения в булевой алгебре, поэтому мы не можем сказать, что A x A =A ² .

Вместо этого мы обнаруживаем, что произведение логической величины и само является исходной величиной, поскольку 0 x 0 =0 и 1 x 1 =1 :

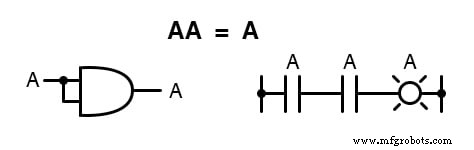
Умножение количества на его дополнение

Четвертое мультипликативное тождество не имеет эквивалента в обычной алгебре, потому что оно использует дополнение к переменной - концепцию, уникальную для булевой математики.

Поскольку должен быть один « 0 ”Значение между любой переменной и ее дополнением, и поскольку произведение любой логической величины и 0 равно 0 , произведение переменной и ее дополнение должно быть 0 :

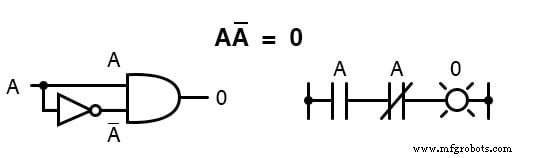
Подводя итог, у нас есть четыре основных логических тождества для сложения и четыре для умножения:

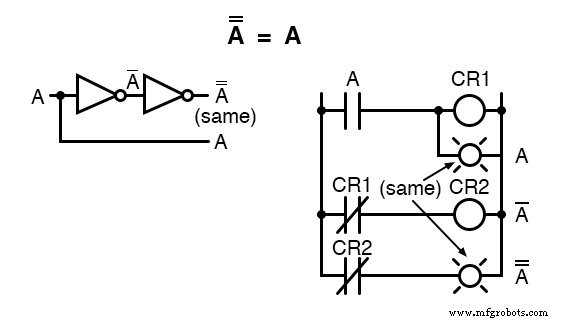
Двойное дополнение

Еще одна идентичность, связанная с дополнением, - это двойное дополнение :переменная, дважды инвертированная.

Двойное дополнение переменной (или любое четное количество раз) дает исходное логическое значение.

Это аналогично отрицанию (умножению на -1) в алгебре действительных чисел:четное число отрицаний отменяется, чтобы оставить исходное значение:

СВЯЗАННЫЕ РАБОЧИЕ ТАБЛИЦЫ:

• Рабочий лист булевой алгебры