Логическая арифметика

Давайте начнем изучение булевой алгебры с сложения чисел:

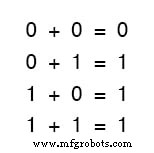
Первые три суммы понятны любому, кто знаком с элементарным сложением.

Однако последняя сумма, вполне возможно, является причиной большей путаницы, чем любое другое отдельное утверждение в цифровой электронике, поскольку кажется, что она противоречит основным принципам математики.

Что ж, это противоречит принципам сложения действительных чисел, но не логических чисел.

Помните, что в мире булевой алгебры есть только два возможных значения для любой величины и для любой арифметической операции:1 или 0.

В области логических значений не существует такой вещи, как «2». Поскольку сумма «1 + 1» определенно не равна 0, она должна быть равна 1 в процессе исключения.

Неважно, сколько или мало терминов мы сложим вместе. Рассмотрим следующие суммы:

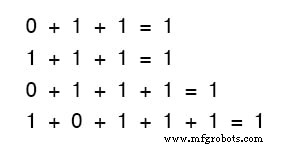
ИЛИ Выход

Внимательно посмотрите на двухчленные суммы в первой системе уравнений.

Вам этот образец кажется знакомым? Должно! Это тот же образец единиц и нулей, что и в таблице истинности для логического элемента ИЛИ.

Другими словами, логическое сложение соответствует логической функции элемента «ИЛИ», а также параллельных контактов переключателя:

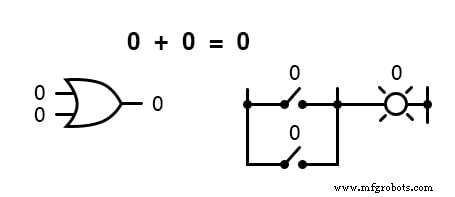
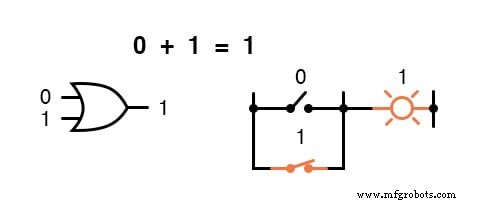
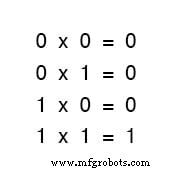
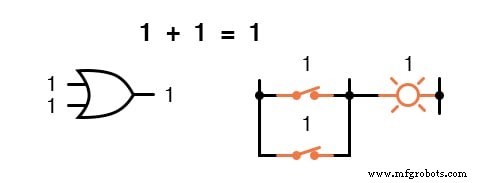
В области логической математики не существует такого понятия, как вычитание.

Вычитание подразумевает наличие отрицательных чисел: 5–3 . это то же самое, что 5 + (-3) , а в булевой алгебре отрицательные величины запрещены.

В логической математике тоже нет такого понятия, как деление, поскольку деление на самом деле не что иное, как сложное вычитание , точно так же, как умножение - это сложное сложение .

И ворота

Умножение допустимо в булевой алгебре, и, к счастью, оно такое же, как и в алгебре действительных чисел:все, что умножается на 0 равно 0 , и все, что умножено на 1 остается без изменений:

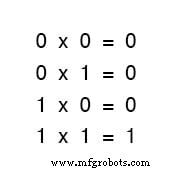
Этот набор уравнений также должен показаться вам знакомым:это тот же образец, что и в таблице истинности для логического элемента AND.

Другими словами, логическое умножение соответствует логической функции « И »Ворот, а также к контактам последовательного переключателя:

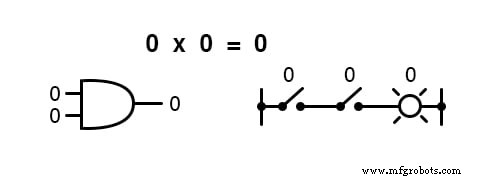
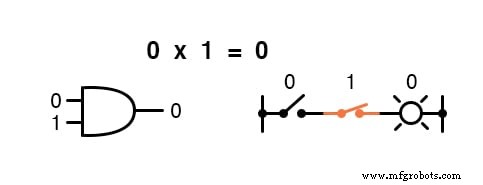
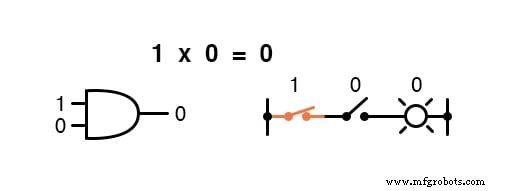
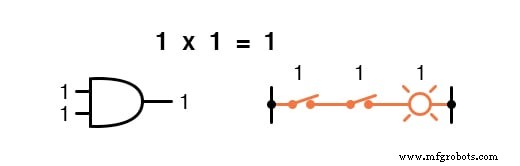
Как и в «нормальной» алгебре, в булевой алгебре для обозначения переменных используются буквы алфавита.

Однако, в отличие от «нормальной» алгебры, логические переменные всегда ЗАГЛАВНЫМИ буквами, а не строчными.

Поскольку им разрешено принимать только одно из двух возможных значений, либо 1 или 0 , каждая переменная имеет дополнение :противоположность его значения.

Например, если переменная « A "Имеет значение 0 , затем дополнение к A имеет значение 1 .

В логической записи используется черта над символом переменной для обозначения дополнения, например:

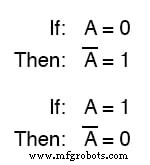
НЕ Ворота

В письменной форме дополнение к « A »Обозначается как« А-нет »Или« А-бар ». Иногда для обозначения дополнения используется символ «штрих».

Например, A ’Будет дополнением к A , почти так же, как использование символа штриха для обозначения дифференцирования в исчислении, а не дробной записи d / dt .

Однако обычно символ «полоса» находит более широкое применение, чем « штрих . »По причинам, которые станут более очевидными позже в этой главе.

Логическое дополнение находит эквивалент в форме элемента НЕ , или нормально замкнутый переключатель или релейный контакт:

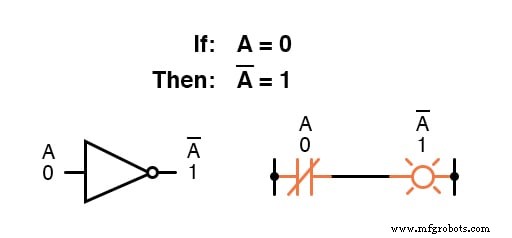
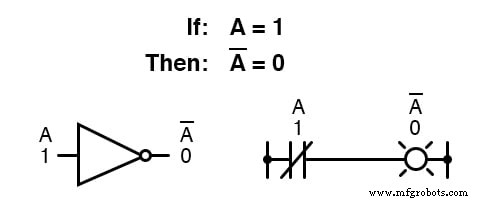
Базовое определение логических величин привело к простым правилам сложения и умножения и исключило как вычитание, так и деление как допустимые арифметические операции.

У нас есть символы для обозначения логических переменных и их дополнений. В следующем разделе мы перейдем к разработке логических идентификаторов.

ОБЗОР:

• Логическое сложение эквивалентно ИЛИ логическая функция, а также параллельные переключающие контакты.
• Логическое умножение эквивалентно операции И логическая функция, а также последовательные переключающие контакты.
• Логическое дополнение эквивалентно НЕ логическая функция, а также нормально закрытый контакты реле.

СВЯЗАННЫЕ РАБОЧИЕ ТАБЛИЦЫ:

• Рабочий лист булевой алгебры