Арифметика комплексных чисел

Поскольку комплексные числа являются допустимыми математическими объектами, как и скалярные числа, их можно складывать, вычитать, умножать, делить, возводить в квадрат, инвертировать и т. Д., Как и любые другие числа.

Некоторые научные калькуляторы запрограммированы на выполнение этих операций непосредственно с двумя или более комплексными числами, но эти операции также можно выполнять «вручную». В этом разделе показано, как выполняются основные операции.

Это высоко рекомендуется вооружиться научным калькулятором, способным легко выполнять арифметические операции с комплексными числами. Это сделает ваше изучение цепи переменного тока намного более приятным, чем если бы вы были вынуждены выполнять все расчеты в течение длительного времени.

Сложение и вычитание комплексных чисел прямоугольной формы

Сложение и вычитание с комплексными числами в прямоугольной форме очень просто. Для сложения просто сложите действительные компоненты комплексных чисел, чтобы определить действительную составляющую суммы, и сложите мнимые компоненты комплексных чисел, чтобы определить мнимую составляющую суммы:

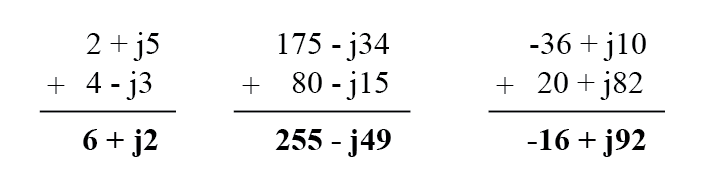
При вычитании комплексных чисел в прямоугольной форме просто вычтите действительную составляющую второго комплексного числа из действительной составляющей первого, чтобы получить действительную составляющую разности, и вычтите мнимую составляющую второго комплексного числа из мнимой составляющей первым пришла мнимая составляющая различия:

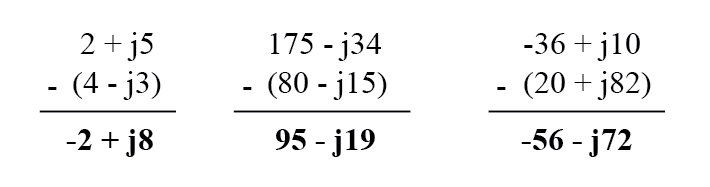
Умножение и деление комплексных чисел в полярной форме

Для обычного умножения и деления предпочтительнее использовать полярную нотацию. При умножении комплексных чисел в полярной форме просто умножайте полярные величины комплексных чисел, чтобы определить полярную величину произведения, и добавить углы комплексных чисел для определения угла изделия:

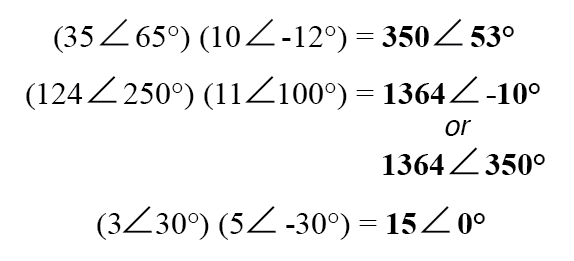
Делить комплексные числа в полярной форме также легко:просто разделите полярную величину первого комплексного числа на полярную величину второго комплексного числа, чтобы получить полярную величину частного, и вычтите угол второго комплексного числа из угол первого комплексного числа, который должен быть равен углу частного:

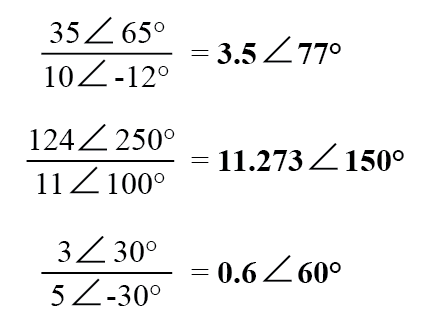
Чтобы получить обратное или «инвертировать» (1 / x) комплексное число, просто разделите число (в полярной форме) на скалярное значение 1, которое является не чем иным, как комплексным числом без мнимой составляющей (угол =0):

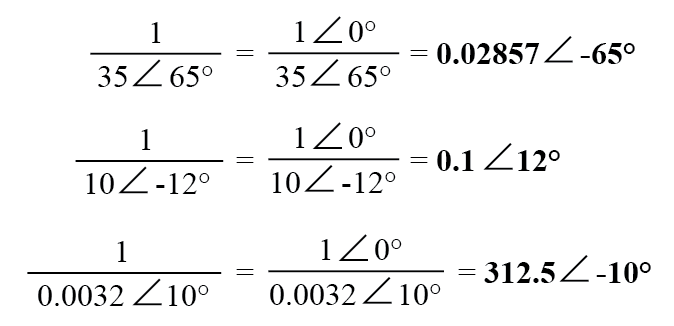
Это основные операции, которые вам необходимо знать, чтобы управлять комплексными числами при анализе цепей переменного тока. Однако операции с комплексными числами ни в коем случае не ограничиваются только сложением, вычитанием, умножением, делением и инверсией.

Практически любая арифметическая операция, которая может быть выполнена со скалярными числами, может выполняться с комплексными числами, включая степени, корни, решение одновременных уравнений с комплексными коэффициентами и даже тригонометрические функции (хотя это включает в себя совершенно новую перспективу в тригонометрии, называемую гиперболическими функциями что выходит далеко за рамки данного обсуждения).

Убедитесь, что вы знакомы с основными арифметическими операциями сложения, вычитания, умножения, деления и инверсии, и у вас не будет проблем с анализом цепей переменного тока.

ОБЗОР:

• Чтобы сложить комплексные числа в прямоугольной форме, добавьте действительные компоненты и добавьте мнимые компоненты. Вычитание аналогично.
• Чтобы умножить комплексные числа в полярной форме, умножьте величины и сложите углы. Чтобы разделить, разделите величины и вычтите один угол из другого.

СВЯЗАННЫЙ РАБОЧИЙ ЛИСТ:

• Рабочий лист фазы переменного тока