Решение одновременных уравнений:метод подстановки и метод сложения

Что такое одновременные уравнения и системы уравнений?

Термины одновременные уравнения и системы уравнений относятся к условиям, при которых две или более неизвестных переменных связаны друг с другом посредством равного количества уравнений.

Пример:

Для этого набора уравнений существует только одна комбинация значений для x и y это удовлетворит обоих.

Любое уравнение, рассматриваемое отдельно, имеет бесконечное множество допустимых значений (x, y) решения, но вместе здесь только один. На графике это условие становится очевидным:

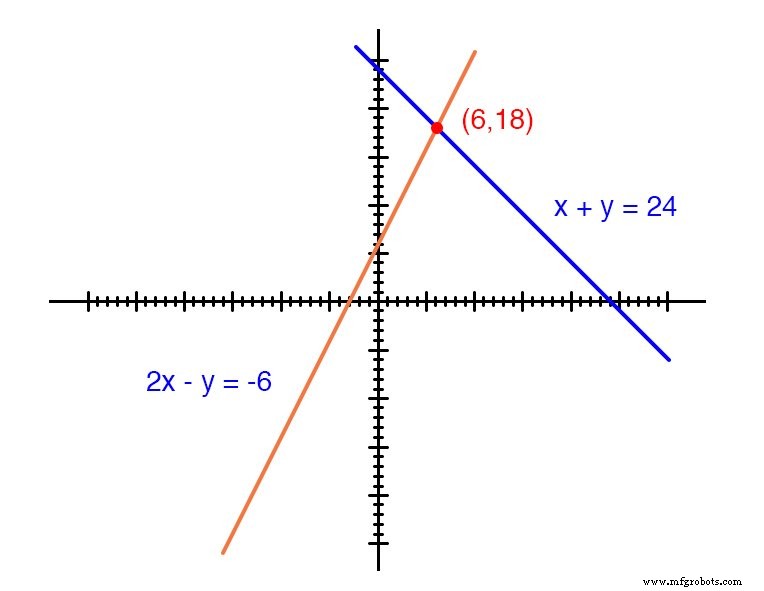
Каждая линия на самом деле представляет собой континуум точек, представляющих возможные x и y пары решений для каждого уравнения.

Каждое уравнение по отдельности имеет бесконечное количество упорядоченных пар ( x , y ) решения. Есть только одна точка, где две линейные функции x + y =24 и 2x - y =-6 пересекаются (где одно из их множества независимых решений работает для обоих уравнений), и именно здесь x равен значению 6 и y равно значению 18.

Однако обычно построение графиков не является очень эффективным способом определения набора одновременных решений для двух или более уравнений. Это особенно непрактично для систем из трех и более переменных.

В системе с тремя переменными, например, решение будет найдено путем пересечения трех плоскостей в трехмерном координатном пространстве - сценарий, который нелегко представить.

Решение одновременных уравнений методом подстановки

Существует несколько алгебраических методов решения одновременных уравнений.

Возможно, самый простой для понимания - это подстановка метод.

Возьмем, к примеру, нашу примерную задачу с двумя переменными:

В методе подстановки мы манипулируем одним из уравнений таким образом, чтобы одна переменная определялась в терминах другой:

Затем мы берем это новое определение одной переменной и заменителем это для той же переменной в другом уравнении.

В данном случае мы берем определение y , что составляет 24 - x и замените это на y член, найденный в другом уравнении:

Теперь, когда у нас есть уравнение с одной переменной ( x ), мы можем решить ее, используя «обычные» алгебраические методы:

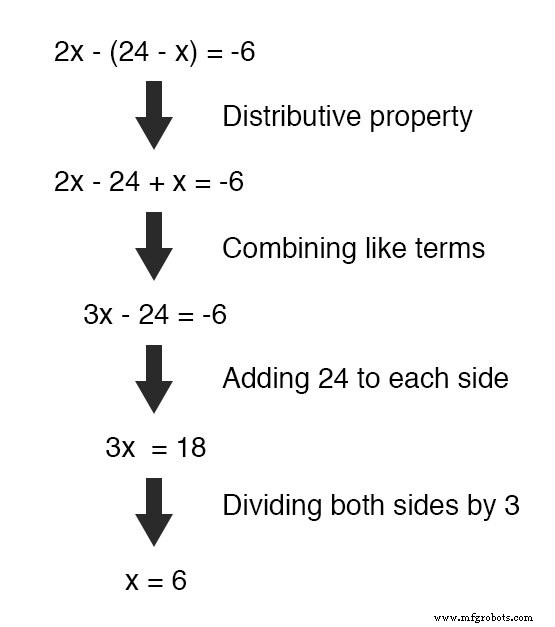
Теперь, когда x известно, мы можем подставить это значение в любое из исходных уравнений и получить значение для y.

Или, чтобы сэкономить нам немного времени, мы можем вставить это значение (6) в уравнение, которое мы только что сгенерировали, чтобы определить y с точки зрения x , поскольку он уже находится в форме для решения для y :

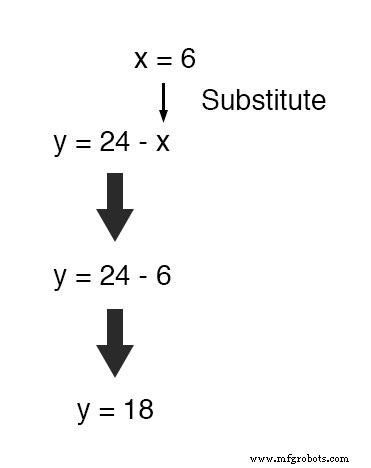
Применение метода подстановки к системам из трех или более переменных включает аналогичный шаблон, только с дополнительными усилиями.

Обычно это верно для любого метода решения:количество шагов, необходимых для получения решения, быстро увеличивается с каждой дополнительной переменной в системе.

Чтобы решить для трех неизвестных переменных, нам нужно как минимум три уравнения. Рассмотрим этот пример:

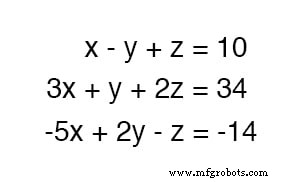
Поскольку первое уравнение имеет простейшие коэффициенты (1, -1 и 1 для x , y и z соответственно), кажется логичным использовать его для разработки определения одной переменной в терминах двух других.

Решить относительно x с точки зрения y и z :

Теперь мы можем заменить это определение x где x появляется в двух других уравнениях:

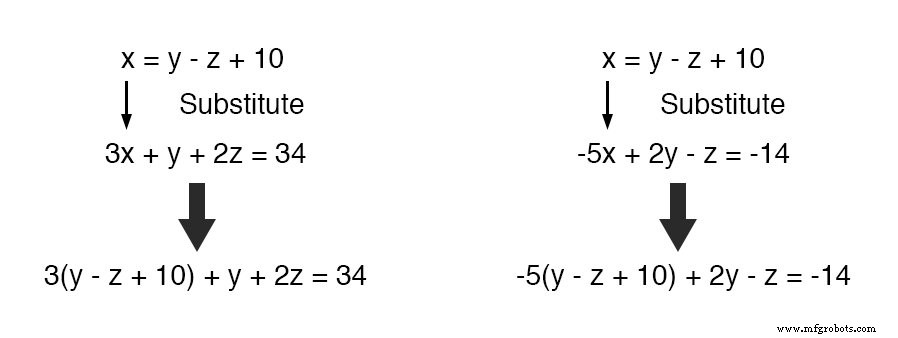
Приведем эти два уравнения к их простейшей форме:

К настоящему времени наши усилия позволили свести систему с трех переменных в трех уравнениях к двум переменным в двух уравнениях.

Теперь мы можем снова применить технику подстановки к двум уравнениям 4y - z =4 и -3y + 4z =36 решить для y или z . Сначала я манипулирую первым уравнением, чтобы определить z с точки зрения y :

Затем мы заменим это определение z с точки зрения y где мы видим z в другом уравнении:

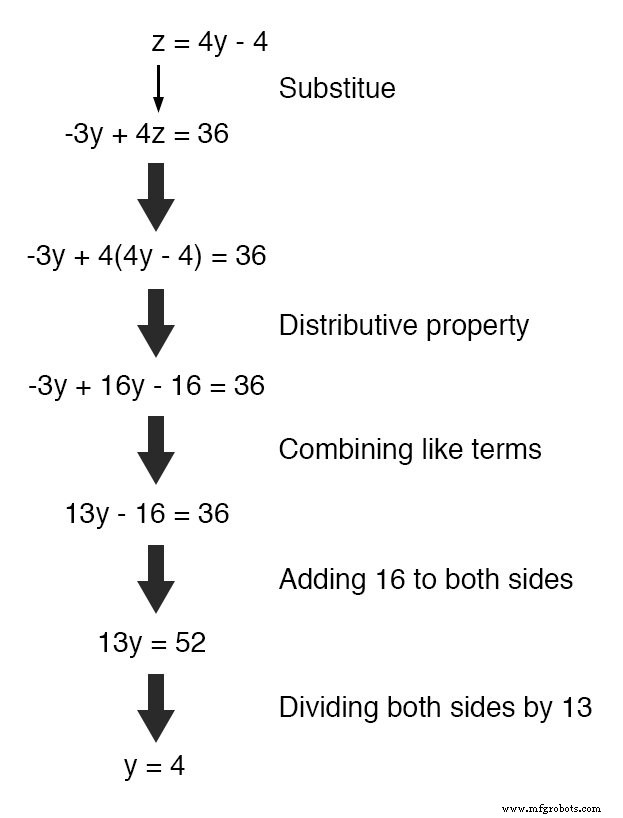
Теперь, когда y - известное значение, мы можем подставить его в уравнение, определяющее z с точки зрения y и получить цифру для z :

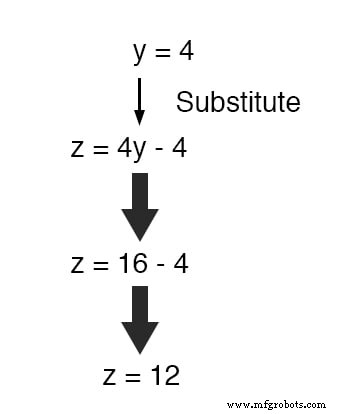
Теперь со значениями для y и z известно, мы можем вставить их в уравнение, в котором мы определили x с точки зрения y и z , чтобы получить значение для x :

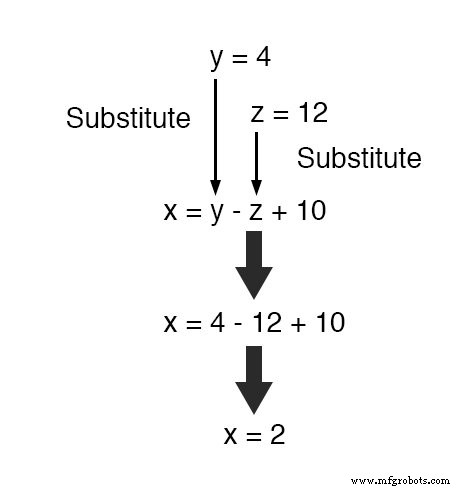
В заключение, мы нашли значения для x , y и z из 2, 4 и 12 соответственно, которые удовлетворяют всем трем уравнениям.

Решение одновременных уравнений с использованием метода сложения

Хотя метод подстановки может быть самым простым для понимания на концептуальном уровне, нам доступны и другие методы решения.

Одним из таких методов является так называемое сложение метод, при котором уравнения добавляются друг к другу с целью исключения переменных членов.

Давайте возьмем нашу систему с двумя переменными, используемую для демонстрации метода подстановки:

Одно из наиболее часто используемых правил алгебры заключается в том, что вы можете выполнять любую арифметическую операцию с уравнением, если вы делаете это одинаково для обеих сторон . .

Что касается сложения, это означает, что мы можем добавить любое количество, которое пожелаем, к обеим сторонам уравнения - при условии, что оно одинаково . количество - без изменения истинности уравнения.

У нас есть возможность сложить соответствующие части уравнений вместе, чтобы сформировать новое уравнение.

Поскольку каждое уравнение является выражением равенства (одинаковое количество по обе стороны от = знак), добавление левой части одного уравнения к левой части другого уравнения допустимо, если мы также складываем вместе правые части двух уравнений.

В нашем примере набора уравнений, например, мы можем добавить x + y в 2x - y и добавьте 24 и -6 вместе, чтобы сформировать новое уравнение.

Какая польза от этого для нас? Изучите, что происходит, когда мы делаем это с нашим примером набора уравнений:

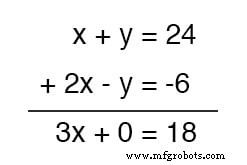
Поскольку в верхнем уравнении оказалось положительное значение y член, в то время как нижнее уравнение содержало отрицательное значение y срок, эти два термина отменяют друг друга в процессе добавления, не оставляя y срок в сумме.

У нас осталось новое уравнение, но с единственной неизвестной переменной x ! Это позволяет нам легко найти значение x :

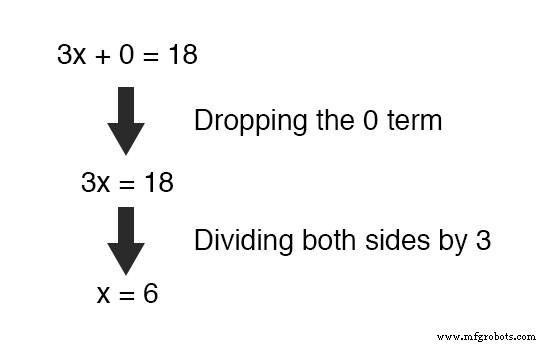
Как только у нас будет известное значение для x , конечно, определяя y Значение - это просто вопрос подстановки (замена x с номером 6 ) в одно из исходных уравнений.

В этом примере метод сложения уравнений хорошо сработал для создания уравнения с единственной неизвестной переменной.

А как насчет примера, когда все не так просто? Рассмотрим следующий набор уравнений:

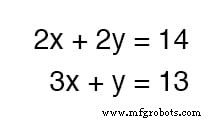
Мы могли бы сложить эти два уравнения вместе - это вполне допустимая алгебраическая операция, - но это не принесет нам пользы для получения значений для x и y :

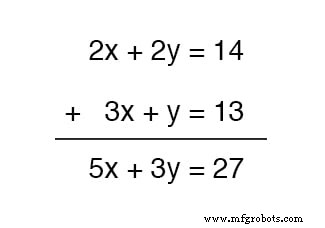
Полученное уравнение по-прежнему содержит две неизвестные переменные, как и исходные уравнения, поэтому мы не продвинемся дальше в поиске решения.

Однако что, если бы мы могли манипулировать одним из уравнений, чтобы получить отрицательный член, который будет отменить соответствующий член в другом уравнении при добавлении?

Затем система сведется к одному уравнению с единственной неизвестной переменной, как в последнем (случайном) примере.

Если бы мы только могли повернуть y член нижнего уравнения в - 2y термин, так что когда два уравнения были сложены вместе, оба y члены в уравнениях будут сокращены, и нам останется только x срок, это приблизит нас к решению.

К счастью, сделать это несложно. Если мы умножим каждый член нижнего уравнения на -2 , это даст результат, который мы ищем:

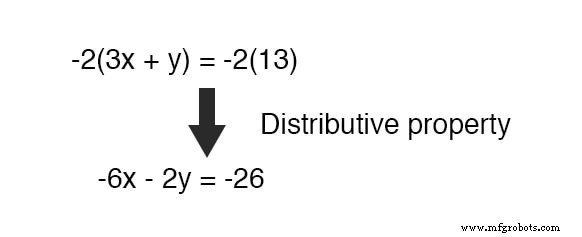
Теперь мы можем добавить это новое уравнение к исходному, верхнему уравнению:

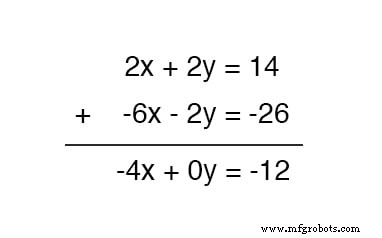
Решение для x , получаем значение 3 :

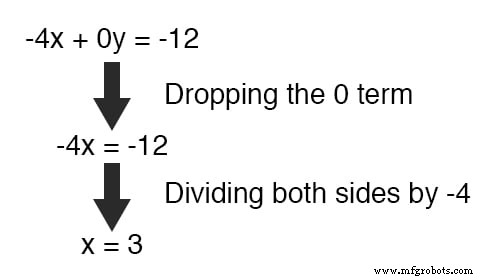
Подставляя это новое значение вместо x в одно из исходных уравнений, значение y легко определяется:

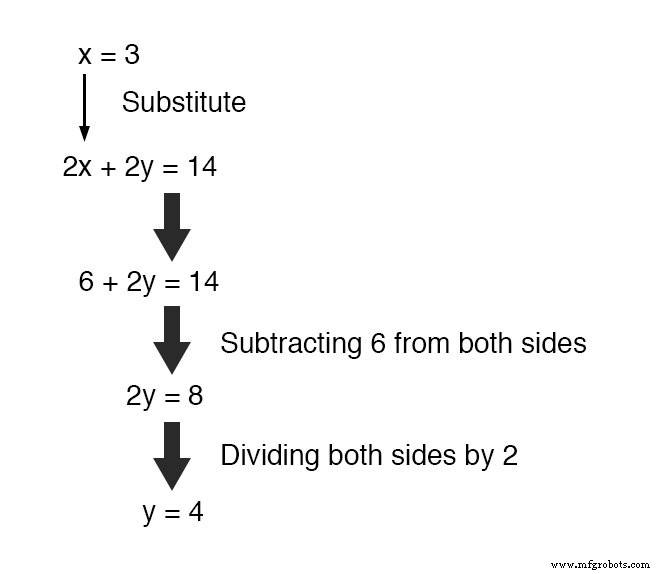
Использование этого метода решения в системе с тремя переменными немного сложнее.

Как и в случае с заменой, вы должны использовать этот метод, чтобы уменьшить систему из трех уравнений с тремя переменными до двух уравнений с двумя переменными, а затем применить его снова, чтобы получить одно уравнение с одной неизвестной переменной.

Для демонстрации я воспользуюсь системой уравнений с тремя переменными из раздела о заменах:

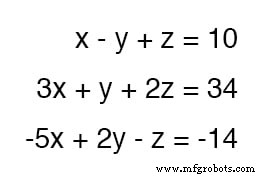
Поскольку верхнее уравнение имеет значения коэффициентов 1 для каждой переменной это будет простое уравнение, которое можно будет использовать в качестве инструмента отмены.

Например, если мы хотим отменить 3x член из среднего уравнения, все, что нам нужно сделать, это взять верхнее уравнение, умножить каждый из его членов на -3 , затем добавьте его к среднему уравнению следующим образом:

Мы можем избавить нижнее уравнение от его -5x таким же образом:возьмите исходное верхнее уравнение, умножьте каждый из его членов на 5 , затем добавьте это измененное уравнение к нижнему уравнению, оставив новое уравнение только с y и z условия:

На данный момент у нас есть два уравнения с теми же двумя неизвестными переменными, y и z :

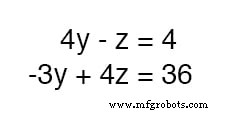
При осмотре должно быть очевидно, что -z член верхнего уравнения может быть использован для отмены 4z член в нижнем уравнении, если только мы умножим каждый член верхнего уравнения на 4 и сложите два уравнения вместе:

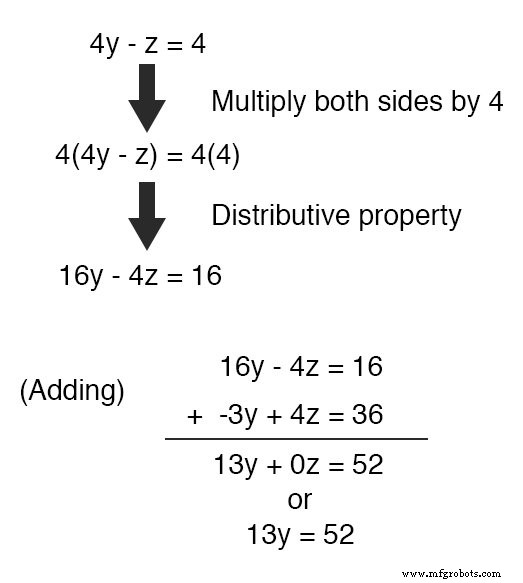
Принимая новое уравнение 13y =52 и решение для y (разделив обе стороны на 13 ) получаем значение 4 для y .

Подставляя это значение 4 для y в любом из уравнений с двумя переменными позволяет нам решить для z .

Подставляя оба значения y и z в любое из исходных уравнений с тремя переменными позволяет нам решить для x .

Конечный результат (я избавлю вас от алгебраических шагов, поскольку они уже должны быть вам знакомы!): x =2 , y =4 и z =12 .

СВЯЗАННЫЕ РАБОЧИЕ ТАБЛИЦЫ:

• Таблица одновременных уравнений для анализа цепей