Горячие графеновые и горячие графеновые нанотрубки:новые низкоразмерные полуметаллы и полупроводники
Аннотация
Мы сообщаем о новом аллотропе графена под названием HOT графен, содержащий углеродные шестиугольники, восьмиугольники и четырехугольники. Соответствующая серия нанотрубок также создается путем сворачивания HOT лист графена. Расчеты ab initio выполняются на геометрических и электронных структурах HOT графен и ГОРЯЧИЙ графеновые нанотрубки. Конус Дирака и высокая скорость Ферми достигаются в негексагональной структуре HOT графен, подразумевая, что сотовая структура не является обязательным условием существования фермионов Дирака. ГОРЯЧИЕ Графеновые нанотрубки демонстрируют отличительные электронные структуры в зависимости от их топологии. (0,1) n ( нет ≥ 3) ГОРЯЧЕЕ графеновые нанотрубки проявляют характеристики полуметаллов, в то время как другой набор нанотрубок (1,0) n показывает плавно регулируемую ширину запрещенной зоны (0 ~ 0,51 эВ) с размером трубки. Конкуренция между эффектом кривизны и приближением сворачивания зон определяет ширину запрещенной зоны (1,0) n нанотрубки. Новое преобразование между полуметалличностью и полупроводимостью возникает в сверхмалых трубках (радиус <4 Å, то есть n <3).
Введение
Благодаря своей гибкости соединения углеродные системы демонстрируют неограниченное количество различных структур с одинаково большим разнообразием физических свойств. Эти физические свойства в значительной степени являются результатом размерности этих структур [1]. Графен представляет собой единый двумерный слой атомов углерода, связанных в гексагональную решетчатую структуру [2], проявляющий ряд уникальных свойств, таких как безмассовые носители, высокая скорость Ферми [3] и конусы Дирака [4, 5], которые являются характеристика двумерных фермионов Дирака. Сотовая решетка, состоящая из двух эквивалентных углеродных подрешеток, играет решающую роль в формировании таких интригующих свойств [2]. Еняшин и Ивановский [6] построили 12 искусственных двумерных углеродных сетей, но не обнаружили никаких структур, кроме аллотропа графина, которые демонстрируют электронное поведение, подобное графену. Похоже, это означает, что дираковские фермионы в sp 2 углеродные системы со связями зависят от сотовой структуры. В нижнем измерении углеродная нанотрубка представляет собой сотовую структуру, свернутую в полый цилиндр с нанометрическим диаметром и длиной в мкм [7,8,9,10]. Поскольку существует бесконечное количество способов свертывания листа в цилиндр, большое разнообразие возможных спиральных геометрий, определяющих хиральность трубки, обеспечивает семейство нанотрубок с разными диаметрами и микроскопическими структурами [11,12,13]. Электронные и транспортные свойства, безусловно, являются одними из наиболее важных физических свойств углеродных нанотрубок и в решающей степени зависят от диаметра и хиральности [14,15,16,17,18]. Графеновые нанотрубки могут быть полуметаллическими [14] или полупроводниковыми [19,20,21] с шириной запрещенной зоны от нуля до нескольких десятых эВ в зависимости от их диаметра и хиральности [10, 14, 16]. Кроме того, можно показать, что запрещенная зона полупроводниковых трубок просто связана с диаметром трубки. Полуметаллические нанотрубки также сохраняют уникальные свойства графена, такие как безмассовые носители, высокая скорость Ферми [22] и конусы Дирака [23]. Такие замечательные результаты могут быть получены из множества соображений, начиная с так называемого подхода сворачивания полос, основанного на знании электронных свойств графенового листа, до прямого исследования нанотрубок с использованием полуэмпирических подходов сильной связи [14, 16, 18, 23]. По сравнению с более сложными расчетами ab initio и доступными экспериментальными результатами, более тонкие соображения, такие как эффекты кривизны, k F сдвиг [24, 25], σ-π-гибридизация [26]. Графен и графеноподобные материалы [6] считаются революционным материалом для будущего поколения высокоскоростных электронных устройств, радиочастотных логических устройств [27, 28], термически и электропроводящих армированных композитов [29, 30], катализаторов [31], датчики [32,33,34,35], прозрачные электроды [27, 36] и т. д., основываясь на всех вышеперечисленных необычных свойствах. За последние несколько десятилетий углеродные нанотрубки также показали большой потенциал в логических схемах, хранении газа, катализе и хранении энергии из-за их исключительных электронных, механических и структурных свойств [37,38,39]. Следовательно, создание новых углеродных аллотропов (включая 2D и 1D) было в центре внимания многочисленных теоретических и экспериментальных исследований из-за их фундаментального научного и технологического значения [40]. Однако полное выяснение структуры этих возбуждающих углеродных фаз с помощью современных экспериментальных технологий обычно нереально из-за их ограниченного количества, а также смеси других фаз. Теоретическое предсказание необходимо и принесло большой успех [31,32,33,34,35, 40,41,42].
В этом исследовании мы разработали новый аллотроп графена, который имеет двумерные фермионы Дирака без исключительно гексагональной структуры. Новый аллотроп был построен из переплетенных углеродных шестиугольников, восьмиугольников и четырехугольников и получил название HOT графен. ГОРЯЧИЕ графеновые нанотрубки также были созданы путем свертывания HOT лист графена вместе с разными направлениями. Электронное свойство, эффект кривизны, k F эффект смещения и т. д. HOT графен и нанотрубки были рассчитаны с использованием ab initio расчетов на основе теории функции плотности (DFT).
Метод расчета
Настоящие расчеты по HOT графен и HOT графеновые нанотрубки были созданы с использованием метода первых принципов, основанного на теории функционала плотности (DFT) с обобщенным градиентным приближением (GGA) в форме обменно-корреляционного функционала Perdew-Burke-Ernzerh (PBE) [43], поскольку реализован в Венском пакете моделирования Ab initio (VASP) [44, 45]. Волновые функции были разложены по плоским волнам до отсечки кинетической энергии плоских волн 520 эВ. Интегралы зоны Бриллюэна (BZ) были выполнены с использованием схемы выборки Монкхорста-Пак [46] с k разрешение сетки 2π × 0,03 Å - 1 . Базисные векторы элементарной ячейки (представляющие форму и размер элементарной ячейки) и координаты атомов были полностью ослаблены в каждой системе до тех пор, пока силы, действующие на все атомы, не стали меньше 0,01 эВ / Å.
Результаты и обсуждение
Геометрические и электронные структуры HOT Графен
Геометрическая структура HOT графен (рис. 1а) показывает более сложную ситуацию связывания, чем графен. Разнообразие углеродных полигонов в HOT графен приводит к различным характеристикам углеродных связей. Эти многоугольники в HOT графен имеет общие края друг с другом, и связи можно различить по двум многоугольникам, которым они принадлежат. Поэтому в нашем исследовании они обозначаются как 6–8 связей, 4–8 связей, 4–6 связей, 6–6 связей и 8–8 связей. Связи 4–8 и связи 6–8 имеют две разные длины связи:1,44 Å и 1,47 Å для связей 4–8; 1,41 Å и 1,48 Å для 6–8 связей. Связи 4–6, 6–6 и 8–8 имеют уникальную длину связи 1,44 Å, 1,46 Å и 1,34 Å соответственно. На рисунке 1b показаны зонная структура и плотность состояний (DOS) HOT . графен с соответствующей ЗБ, изображенной на рис. 1в. Точка пересечения энергетических зон на уровне Ферми указывает на полуметалличность HOT графена, что подтверждается исчезновением плотности состояний на уровне Ферми. Точка Дирака расположена в точке (0, 0,0585, 0), смежной с Γ. Трехмерная зонная структура (рис. 2) представляет собой зонные поверхности вблизи уровня Ферми, где можно увидеть конусы Дирака, образованные верхней и нижней коническими поверхностями, пересекающимися в двух точках Дирака точно на поверхности Ферми. Соответствующая скорость Ферми (v F ) фермионов Дирака, рассчитанная по градиенту линейных дисперсий зонных структур, составляет 6,27 × 10 5 м / с, что немного ниже 8,1 × 10 5 м / с [22] для графеновой нанотрубки и 8,6 × 10 5 м / с [47, 48] для графена. Высокий v F подразумевает высокую мобильность перевозчиков в HOT графен.
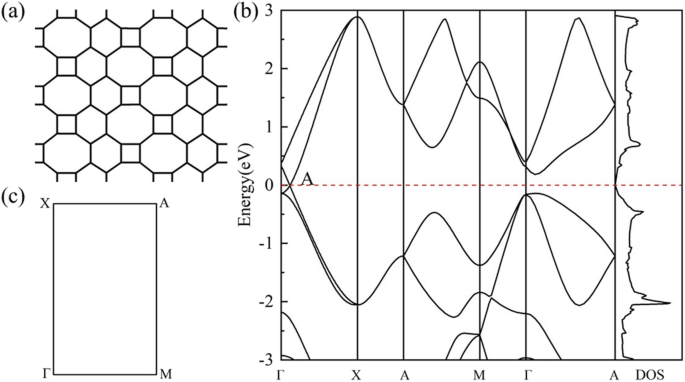
( а ) Геометрия HOT графен; ( б ) Ленточные структуры и DOS HOT графен; ( c ) соответствующий БЖ раздела HOT графен
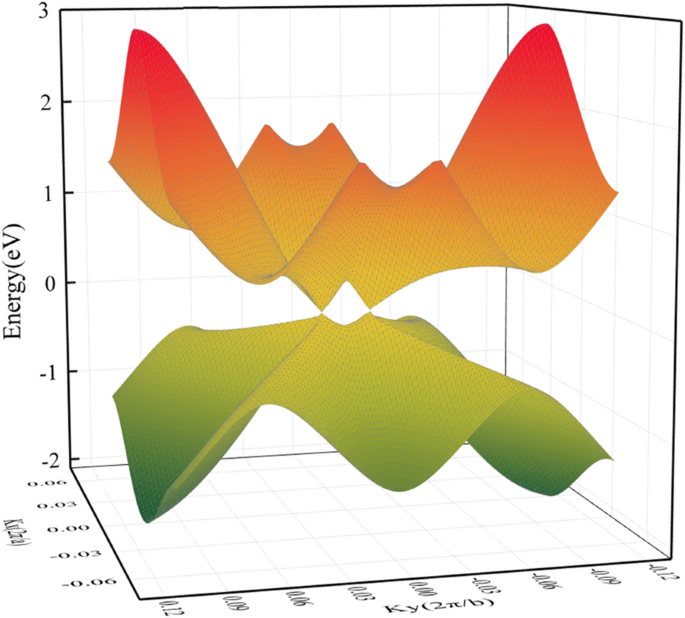
Трехмерная структура полосы HOT графен
Геометрические и электронные структуры HOT Графеновые нанотрубки
HOT графеновые трубки скручиваются из HOT лист графена в различных направлениях, обозначенный индексом на 2D HOT решетка графена (рис. 3а). Этот индекс обозначается как ( l, m ) н на основе двух единичных векторов a и b . Символ ( l, m ) [18, 20, 21] обозначают разные направления на HOT лист графена, n обозначает количество единиц периметра (рис. 3b и c), используемых при намотке труб. Под симметрией обращения пространства HOT элементарная ячейка графена, символ нанотрубки ограничен 0 ≤ l и 0 ≤ м чтобы избежать переписки "многие к одному". Количество возможных геометрических структур HOT Количество графеновых нанотрубок бесконечно, поскольку существует бесконечный выбор как диаметров, так и направлений прокатки. Среди такого большого количества нанотрубок в нашем исследовании выбраны только два направления (0,1, 1,0). Это связано с тем, что спиральное расположение атомов в других направлениях едва ли является периодическим и имеет почти бесконечную длину элементарной ячейки вдоль оси трубки. В наших расчетах такая большая элементарная ячейка нереальна. Различные направления качения между (1,0) n и (0,1) n трубы приводят к различиям в геометрии и ситуации соединения. Две трубы (1,0) 6 и (0,1) 4 изображены на рис. 3d и e для описания геометрических различий между двумя направлениями прокатки. Расположение многоугольников по направлению (1,0) можно разделить на два паттерна:C 4 –C 6 –C 8 (оранжевый) и C 8 –C 6 –C 4 (синий), которые прямо противоположны друг другу. Эти два противоположных рисунка чередуются в окружном направлении трубки. В направлении (0,1) многоугольники, расположенные вдоль оси трубы, также имеют два шаблона:C 4 –C 8 (синий) и C 6 –C 6 (апельсин). Два C 4 –C 8 шаблоны чередуются с одним C 6 –C 6 узор по окружности.
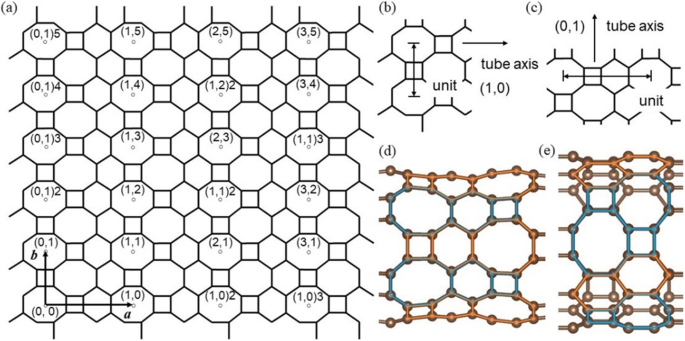
( а ) Различные трубки обозначаются символом ( l, m ) н , с ( l, m ) обозначает направление прокатки на основе единичного вектора a и b , и n по количеству единиц диаметра трубы; ( б ) единица диаметра в направлении (1,0); ( c ) единица диаметра в направлении (0,1); ( д ) геометрическая структура (1,0) 6 HOT графеновая нанотрубка; ( е ) геометрическая структура (0,1) 4 HOT графеновая нанотрубка
Чтобы выявить затраты энергии на сворачивание листа в трубы, мы определяем энергию кривизны (рис. 4) E cur как:
$$ {E} _ {\ mathrm {cur}} ={E} _ {\ mathrm {tube}} ^ {\ mathrm {at}} - {E} _ {\ mathrm {sheet}} ^ {\ mathrm { at}} $$где \ ({E} _ {\ mathrm {tube}} ^ {\ mathrm {at}} \) - средняя энергия атомов в нанотрубке, а \ ({E} _ {\ mathrm {sheet}} ^ {\ mathrm {at}} \) - средняя энергия атомов в 2D-листе. (1,0) n трубки имеют более низкую стоимость энергии, чем графеновые нанотрубки, в то время как (0,1) n трубки почти такие же, как кресельные графеновые нанотрубки, за исключением нескольких сверхмалых трубок. Такие результаты также предполагают, что можно синтезировать HOT графеновые нанотрубки в экспериментах. Следует отметить, что трубка (1,0) 1 слишком мала, потому что ее диаметр даже меньше, чем длина связи углерода.
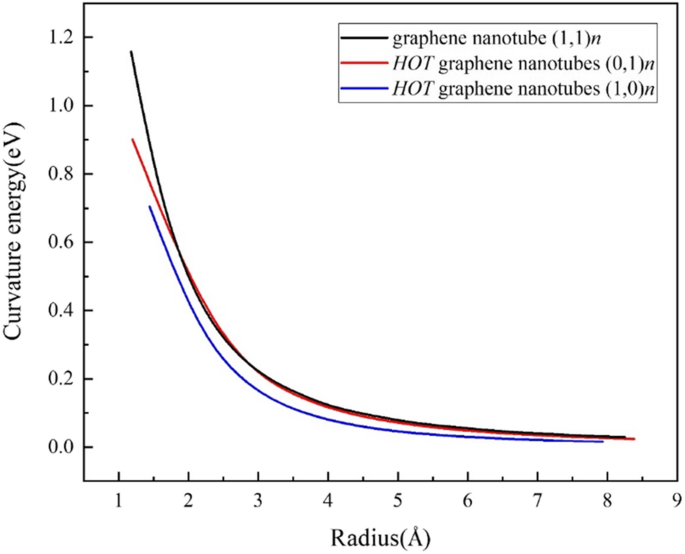
Энергия кривизны HOT графеновые нанотрубки и графеновые нанотрубки
Расчетная электронная зонная структура и плотность состояний нанотрубки (0,1) 6 (рис. 5б) указывают на полуметаллический характер. Когда HOT лист графена свернут в нанотрубку, его 2D BZ уменьшается до 1D BZ в результате новых периодических граничных условий в нанотрубках. Периодические граничные условия вдоль окружного направления трубки допускают только волновые векторы «вокруг» окружности нанотрубки, и эти векторы квантуются [49]. Периодические граничные условия вдоль оси нанотрубки остаются такими же, как и для 2D-листа, тогда волновые векторы остаются непрерывными вдоль оси нанотрубки. Согласно схеме складывания зон, электронная зонная структура конкретной нанотрубки задается наложением электронных энергетических зон соответствующего 2D-листа вдоль специально разрешенного k линии [50]. Поскольку квантованные волновые векторы в середине БЖ HOT графен всегда пересекает точку Дирака (точка F на рис. 5a), невырожденная точка Дирака (точка F на рис. 5b) и конус Дирака появляются в зонных структурах (0,1) n HOT графеновые нанотрубки, в результате чего все (0,1) n нанотрубки. Трубка (0,1) 6 рассчитывается для оценки полуметалличности этого набора (0,1) n нанотрубок на рис. 5. Зонная структура (0,1) 6 HOT Графеновые нанотрубки показывают точку пересечения энергетических зон на уровне Ферми, а соответствующая плотность состояний не показывает состояний на уровне Ферми, что подтверждает полуметалличность системы. Поскольку конус Дирака в (0,1) n пробирки происходят из HOT графенового листа, расчетная координата точки Дирака в нанотрубке (0,1) 6 такая же, как и в HOT лист графена, который равен (0, 0,0585, 0). Расчетная скорость Ферми в точке Дирака в нанотрубке (0,1) 6 составляет 6,76 × 10 5 . м / с, примерно 6,27 × 10 5 м / с в HOT лист графена.
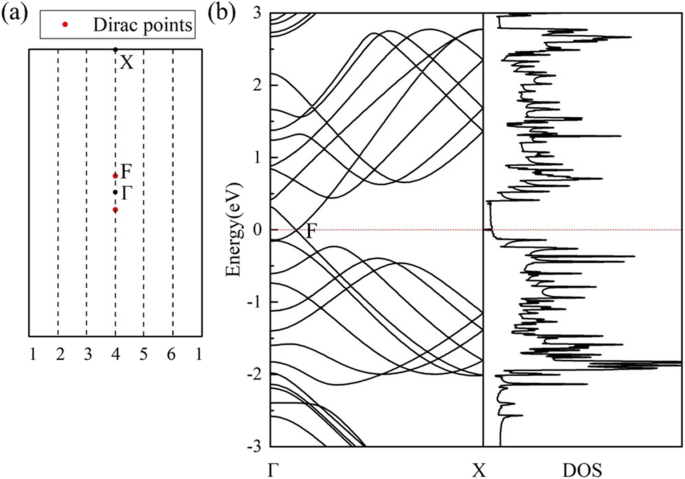
( а ) Первый БЖ раздела HOT графен с допустимым k штриховые линии для нанотрубки (0,1) 6. F - точка Дирака. ( б ) Расчетные зонные структуры и плотность состояний (0,1) 6 нанотрубки
Эволюция зонной структуры (0,1) n нанотрубок с разными радиусами трубок (рис. 6а) показывает, что HOT графеновые нанотрубки (0,1) n полуметаллические ( n ≥ 3) и преобразовать в металл ( n =2), а затем вернуться к полуметаллу ( n =1). Такое изменение при малом радиусе вызвано так называемым эффектом кривизны [26]. В случае сверхмалых нанотрубок (например, (0,1) 2 и (0,1) 1) кривизна оказывает существенное влияние на схему складывания зон. Длина связи и угол связи претерпевают существенные изменения в пределах большой кривизны, которая влияет на структуру электронной зоны. Зонная структура таких нанотрубок больше не является простой суперпозицией энергетических зон на разрешенных волновых векторах. Это изменение облигаций изменяет условия, которые определяют k точка, в которой пересекаются занятые и незанятые полосы (в точке, где мы помечаем k F ) и сдвиньте k F от исходных точек Дирака, которая называется k F эффект сдвига [24, 25]. В результате в (0,1) n HOT графеновые нанотрубки, k F смещается от исходного положения ( k ГОРЯЧИЕ ) в HOT лист графена (точка F на рис. 5а). И направление смещения k F рассчитывается вдоль допустимого волнового вектора (пунктирные линии на рис. 5a), что не приводит к изменению полуметалличности (рис. 6a ( n ) ≥ 3)). Согласно рассчитанной координации точек Дирака, k F эффект смещения становится заметным в точке (0,1) 5 с радиусом трубки 5,988 Å, точка Дирака которой ( k F ) смещается в (0,0.0626,0) от исходной точки ( k ГОРЯЧИЕ ) в (0,0.0594,0) в HOT лист графена. По мере уменьшения радиуса трубы k F продолжает смещаться и достигает точки (0,0.0712,0) в трубке (0,1) 3. В трубке (0,1) 2 k F сдвигается к (0,0.0835,0), где точка Дирака опускается ниже уровня Ферми, что приводит к металлической системе. Исчезновение полуметалличности в (0,1) 2 указывает на отклонение от k F эффект сдвига в (0,1) n нанотрубки ( n ≥ 3). Более того, трубка (0,1) 1 снова становится полуметаллической по своей ленточной структуре и DOS (рис. 6b). Наш анализ электронного состояния (0,1) n HOT нанотрубки показывают π-состояния, перекрывающиеся на n ≥ 2, что обычно считается причиной полуметалличности графеновых нанотрубок [18, 24]. Однако соответствующий анализ электронного состояния HOT Графеновая нанотрубка (0,1) 1 демонстрирует σ-π-гибридизацию, когда низколежащая σ * -полоса пересекает уровень Ферми и соединяется с конусом Дирака (синие линии на рис. 6a). Координация точки Дирака (0,0.18345,0) также отличается от других (0,1) n HOT графеновые нанотрубки. Расчетная скорость Ферми составляет 4,47 × 10 5 . м / с, ниже 6,27 × 10 5 м / с в HOT лист графена и значения для других (0,1) n нанотрубки (~ 6,76 × 10 5 РС). Явно иная форма его зонной структуры также показана на рис. 6а. Все эти символы подтверждают полуметалличность HOT Графеновая нанотрубка (0,1) 1 возникла в результате σ-π-гибридизации. Таким образом, с увеличением кривизны k F эффект смещения проявляется на n =5, становится более эффективным при 4 ≥ n ≥ 2, и, наконец, заменяется эффектом σ-π-гибридизации при n =1.
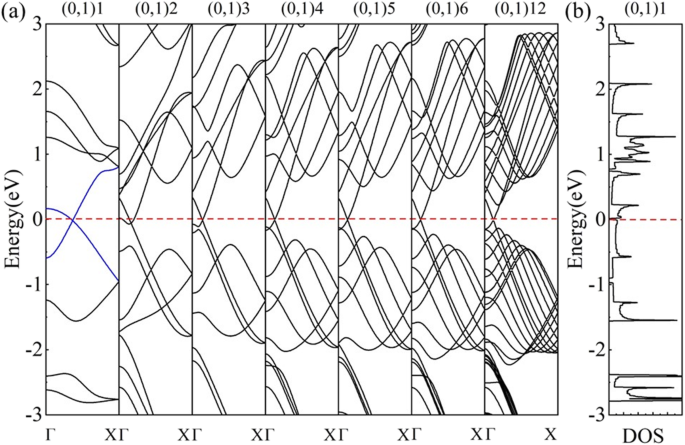
( а ) Ленточная эволюция (0,1) n нанотрубки ( n =1, 2, 3, 4, 5, 6, 12); ( б ) DOS нанотрубки (0,1) 1
В другом направлении прокатки расчетная ленточная структура (1,0) 6 (рис. 7b) показывает полупроводимость. 6 волновых векторов (пунктирные линии) параллельны Γ-M, пересекая точку Г в середине BZ HOT . графена (рис. 7a) и откройте запрещенную зону 0,46 эВ, как показано на DOS (рис. 7b). В этом направлении качения разрешенные волновые векторы в середине BZ никогда не включают точки Дирака, что приводит к ненулевым запрещенным зонам в этом наборе нанотрубок. Эволюция зон показывает изменение запрещенных зон с разными радиусами на рис. 8а. (1,0) n HOT графеновые нанотрубки полупроводниковые ( n ≥ 4). Максимум валентной зоны (VBM) и минимум зоны проводимости (CBM) приближаются от трубки (1,0) 6 к трубке (1,0) 4, а затем пересекаются друг с другом в трубке (1,0) 3 с радиусом 2,17 Å. Эта точка пересечения находится точно на уровне Ферми, расположенном в (0,0791,0,0). Расчетная плотность состояний (рис. 8b) представляет 0 состояний на уровне Ферми (1,0) 3, что подтверждает полуметалличность. Когда радиус трубки уменьшается до (1,0) 2, снова открывается щель 0,848 эВ. CBM и VBM (1,0) 2 расположены в точке Γ и точке M, соответственно, что указывает на непрямую запрещенную зону. Это изменение VBM означает другое происхождение полупроводимости в (1,0) 2. Дальнейшее исследование изменения ширины запрещенной зоны в (1,0) n HOT Графеновые нанотрубки показаны на рис. 9. Эволюция запрещенной зоны как функция n (3 ≤ n ≤ 23) означает, что ширина запрещенной зоны регулируется в зависимости от размера трубки. Кроме того, вместо монотонности зависимость ширины запрещенной зоны от размера трубки имеет зигзагообразную форму (черная кривая на рис. 9). Глобальный минимум (1,0) 15 представляет собой нулевую запрещенную зону. Полуметалличность (1,0) 15 дополнительно подтверждается зонной структурой и DOS (рис. 9g). Из схемы складывания зон мы знаем, что зонная структура нанотрубок является суперпозицией зонной структуры 2D-листа вдоль соответствующего квантованного k линии [50]. Таким образом, полуметалличность указывает на то, что хотя бы один из допустимых k линии (пунктирные линии на рис. 7a) пересекают точки Дирака (красные точки на рис. 7a) в n =15. В противном случае, если разрешено k линии имеют расстояние от точек Дирака ( k ГОРЯЧИЕ ) в нанотрубке появится запрещенная зона. Кроме того, это расстояние между k F и k линии пропорциональны ширине запрещенной зоны, так как дисперсия зон вблизи конуса Дирака линейна [25]. Δk м измеряет кратчайшее расстояние между k F и k м линии квантового числа m . Мы рассчитали это расстояние Δk м между точками Дирака ( k ГОРЯЧИЕ ) и допустимое k строки в HOT графен и изобразите его (красная линия) вместе с запрещенными зонами (черная линия) на рис. 9. Во-первых, все разрешенные k линии имеют квантовое число m . Когда n ≤ 7 (например, рис. 9a), кратчайшее расстояние ( Δk м ) находится между k ГОРЯЧИЕ и первые k линия, k 1 , который постоянно находится в точке Γ (вставьте график (a) на рис. 9). В этой ситуации Δk м постоянна, поскольку оба k 1 и k ГОРЯЧИЕ не зависят от размера трубки. Однако, как разрешено k линии становятся более плотными в более крупных нанотрубках (7 ≤ n ≤ 17), k 2 становится ближайшим к k ГОРЯЧИЕ (например, рис. 9b). В этой ситуации k 2 приближается к точке Дирака от внешнего ЗБ с увеличением радиуса трубы; следовательно, он показывает снижение на Δk м на рис. 9 (7 ≤ n ≤ 17). нет =17 - поворотный момент, когда k 2 почти пересекает точку Дирака, что приводит к локальному минимуму расстояния Δk м (Рис. 9c). По мере увеличения радиуса k 2 пересечь k ГОРЯЧИЕ точки и продолжает двигаться от нее к точке Г, что приводит к увеличению расстояния снова на 17 ≤ n ≤ 24 (например, рис. 9г). В то же время k 3 приближается к точке Дирака. к 3 приближается к k ГОРЯЧИЕ чем k 2 и начинается новое уменьшение расстояния Δk м в n ≥ 24. Поскольку ширина запрещенной зоны пропорциональна этому расстоянию Δk м [25] кривая запрещенной зоны имеет ту же форму, что и Δk м сюжет ( n ≥ 7). И обнаружено, что запрещенные зоны изменяются циклически: k м приближается к точке Дирака ( k ГОРЯЧИЕ ), вызывая уменьшение ширины запрещенной зоны, затем пересекает точку Дирака, приводя к локальному минимуму, затем удаляется от точки Дирака, вызывая увеличение ширины запрещенной зоны, и, наконец, заменяется следующей линией k m + 1 переход в следующий цикл. Таким образом, причина, по которой ширина запрещенной зоны изменяется с размером трубки ( n ≥ 7) заключается в том, что k линии перемещаются с разными размерами трубок, тем самым изменяя расстояние Δk м от k ГОРЯЧИЕ и разрешенное k линий, которые пропорциональны ширине запрещенной зоны.
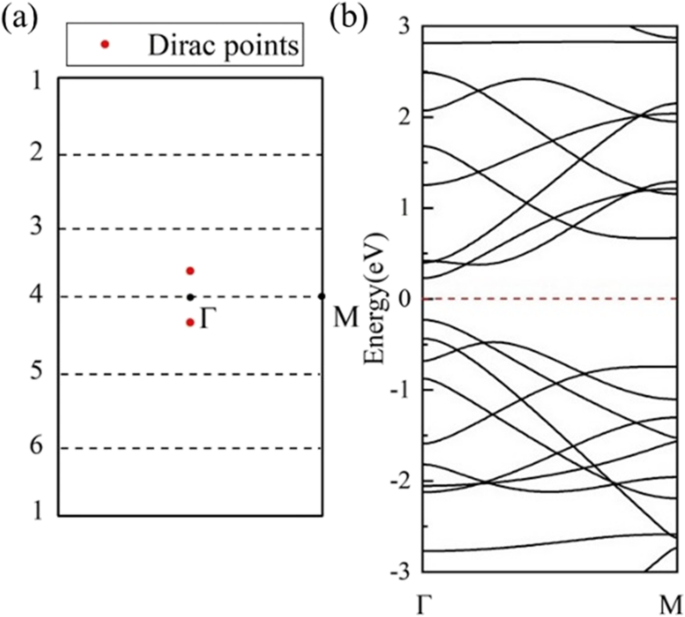
( а ) Первый БЖ раздела HOT графен с допустимым k линии (штриховые линии) для нанотрубки (1,0) 6; ( б ) зонные структуры нанотрубки (1,0) 6
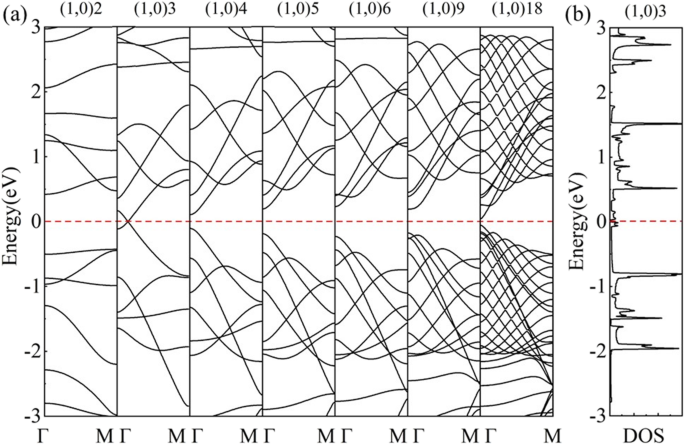
( а ) Эволюция группы HOT графеновые нанотрубки (1,0) n ( n = 2, 3, 4, 5, 6, 9, 18); ( б ) DOS нанотрубки (1,0) 3
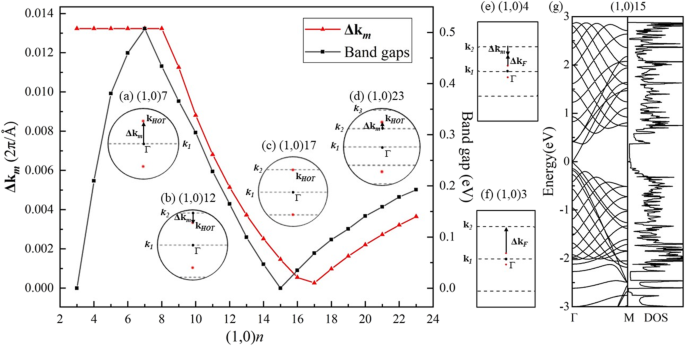
Расчетные запрещенные зоны (черная линия) и расстояние Δk м (красная линия) между k ГОРЯЧИЕ и ближайший k строка в (1,0) n трубки. Вставленные графики - это ЗБ возле точки Γ с допустимым k линии k м ( м =1, 2, 3) (пунктирные линии) и точка Ферми HOT графеновые нанотрубки k ГОРЯЧИЕ (красные точки) в трубке ( a ) (1,0) 7, ( b ) (1,0) 12, ( c ) (1,0) 17, ( d ) (1,0) 23, ( e ) (1,0) 4 и ( f ) (1,0) 3. ( г ) Ленточные структуры и DOS трубки (1,0) 15
Хотя Δk м кривая и кривая запрещенной зоны имеют сходство по форме, различия между ними также очевидны, а именно, что Δk м график показывает «задержку» изменения на n ≥ 7 и полностью отличается от графика ширины запрещенной зоны при 3 ≤ n ≤ 7. Причина в том, что точка Ферми в HOT графеновые нанотрубки ( k F ) предполагается, что она имеет ту же координату, что и исходная точка Ферми в HOT графен ( k ГОРЯЧИЕ ) в предыдущем разделе, где объяснялось изменение ширины запрещенной зоны. Однако точка Ферми ( k F ) в нанотрубках смещается от исходной точки Ферми ( k ГОРЯЧИЕ ) в HOT лист графена под действием кривизны. Таким образом, k F смещение (Δ k F = k F - к ГОРЯЧИЕ ) эффект способствует рассогласованию расстояния Δk м и запрещенные зоны. Как вычислено в (0,1) n трубки (рис. 6), k F в (1,0) n трубки также смещаются к внешнему ЗБ в сторону симметричной точки X под кривизной. Следовательно, когда ближайший k м находится между k ГОРЯЧИЕ и точка Γ - расстояние Δk м занижает ширину запрещенной зоны (например, 17 ≤ n ≤ 24 на рис. 9г). В противном случае ближайшие k м сидит на внешней стороне k ГОРЯЧИЕ точки, это приводит к завышению ширины запрещенной зоны (например, 7 ≤ n ≤ 17 на рис. 9б). В небольших нанотрубках (3 ≤ n ≤ 7), k F эффект смещения усиливается при большом росте кривизны; следовательно, это вызывает резкое k F смещение и изменение ширины запрещенной зоны. Когда радиус становится меньше n =8, k 1 становится ближайшим к k ГОРЯЧИЕ с указанием константы Δk м . Однако k F эффект смещения настолько силен, что перемещает k F дальше от k 1 но ближе к к 2 (Рис. 9e). k F Эффект переключения побеждает в соревновании с k линии движутся и начинает определять запрещенные зоны с тех пор ( n ≤ 7). k F продолжает переходить на k 2 на высокой скорости, так что расстояние между k F и k 2 становится все меньше и меньше. Следовательно, от (1,0) 7 до (1,0) 3 ширина запрещенной зоны уменьшается (рис. 9). Наконец, k F догоняет k 2 и пересекает его в точке n =3 (рис. 9е). Это пересечение k строка с k F приводит к появлению точки Дирака в трубке (1,0) 3, которая приводит к полуметалличности (рис. 8), как обсуждалось в предыдущих разделах. Дальнейшее уменьшение радиуса до n =2 открывает зазор 0,848 эВ в трубке (1,0) 2 (рис. 8). Этот разрыв настолько велик и считается из k F схема переключения передач, и поэтому не показана на рис. 9. Таким образом, существует механизм конкуренции между k линия перемещения и k F смещение при определении ширины запрещенной зоны. k F вводы с эффектом сдвига в маленьких трубках (7 ≥ n ≥ 3), а k линии перемещения выводов в больших трубках ( n ≥ 8), где k F эффект переключения исчезает. Сумма тыс. F смещение оценивается в 0,0015 2π / Å при n =15 и 0,0238 2π / Å при n =3, поскольку ширина запрещенной зоны равна 0 эВ, где сдвинутый k F точка находится на допустимом k линий. Видно, что k F смещение в 15,86 раза больше в маленькой трубке (трубка (1,0) 3), чем в большой трубке (трубка (1,0) 15).
В HOT В графене все атомы углерода имеют трехкратную координацию, поэтому четвертый валентный электрон играет ключевую роль в его проводимости. The calculated band decomposed charge density ± 0.15 eV around the Fermi level (Fig. 10) shows the distribution of the electrons in the Dirac cone. Only the electrons on the 8–8 bonds (Fig. 10a) have an overlapping and the side view (Fig. 10b) shows that the electrons distribute perpendicularly to the HOT graphene sheet, which indicates that the Dirac cone consists of π states. Therefore, the electron overlapping on the 8–8 bonds (enlarged side view in Fig. 10a) is considered to be localized π states. In big nanotubes such as (0,1)6 (Fig. 10c), the charge density is similar to the HOT graphene sheet showing localized π bonds on 8–8 bonds (enlarged side view in Fig. 10c). As the radius decreases to (0,1)2, whose conductivity transforms to metal (Fig. 6), the 8–8 bonds show several deformations (Fig. 10d). Firstly, these states are no longer symmetric with respect to the tube wall. The overlapping of the π state outside the tube wall breaks apart while the π states inside keep overlapping with each other. Besides the 8–8 π bonds, new π bonds form on 4–8 in (0,1)2. These bonds are similar to the deformed 8–8 bonds:separated π states outside the tube wall and overlapping π states inside the tube wall. Every 4–8 bond connects two 8–8 bonds adjacent to it, forming a delocalized π overlapping inside the tube along the tube axis direction. The enlarged side view in Fig. 10d shows the connection between 4 and 8 and 8–8 bonds as a segment of the whole delocalized bond. Therefore, the metallicity in tube (0,1)2 can be attributed to the delocalized π overlapping in the 4–8 and 8–8 bonds along the tube axis direction which provides a pathway for the electrons to travel along the tube. When the radius keeps decreasing, the conductivity disappears and the (0,1)1 tube becomes a semimetal again (Fig. 6). Different from all the other (0,1) n tubes, the 8–8 overlapping (Fig. 10e) in nanotube (0,1)1 is totally broken up; instead, 4–8 overlapping and 4–6 overlapping plays the major role in the Dirac cones. These two bonds belong to two opposite edges in the same carbon tetragons and are arranged parallel to the tube axis. Furthermore, they are no longer π states. Based on the electronic state analysis, a σ-π hybridization takes place at the Fermi level under such a strong curvature in nanotube (0,1)1. It is verified by the charge density which shows the electron states distribute closely to the bond axis (enlarged side view in Fig. 10e). Strongly modified low-lying σ states are introduced at the Fermi level as discussed in the preceding sections (blue line in Fig. 6). Therefore, the σ-π hybrid states in the 4–8 and 4–6 bonds are considered the reason for the semimetallicity in (0,1)1, which is essentially different from the other semimetallic tubes (0,1) n ( нет ≥ 3). In another set of HOT graphene nanotubes, the band gaps show adjustability with different tube radius (Fig. 9). The charge densities also present an evolution with the tube radii in Fig. 11. The band decomposed charge density of tube (1,0)9 in Fig. 11a and b shows the localized π states overlapping in both the VBM and CBM. The VBM is contributed by π states on 6–6 bonds and 8–8 bonds (Fig. 11a). The CBM is contributed by π states on part of 4–8 and 6–8 bonds (Fig. 11b). The 4–6 bonds have no states on both of the VBM and CBM. When the (1,0) n tubes become semimetallic at some specific radii, such as n = 15, the VBM and CBM meet with each other. Band decomposed charge density ± 0.15 eV around the Fermi level of (1,0)15 nanotube show the different distribution of electrons from the semiconductive tubes. More importantly, it exhibits a similar distribution to the semimetallic HOT graphene sheet and (0,1) n tubes. The localized π bond of (1,0)15 only locates on the 8–8 bonds. This redistribution of electron in (1,0) n tubes causes the conductivity change.
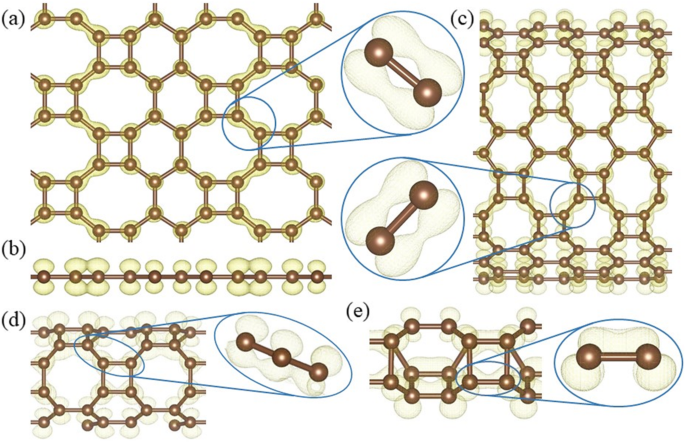
Band decomposed charge densities around the Fermi level of (a ) HOT graphene, (b ) the corresponding side view, and HOT graphene nanotubes (c ) (0,1)6, (d ) (0,1)2, and (e ) (0,1)1 with corresponding enlarged side views
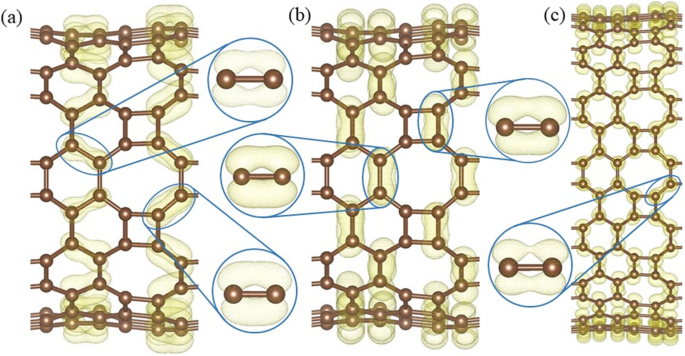
Band decomposed charge densities at (a ) VBM, and (b ) CBM of HOT graphene nanotube (1,0)9; ( c ) charge densities around the Fermi level of the HOT graphene nanotube (1,0)15 with the localized π bond in the enlarged side view
Заключение
A new graphene allotrope named HOT graphene is constructed by carbon hexagons, octagons, and tetragons showing Dirac cone and high Fermi velocity, which implies that the honeycomb structure is not an indispensable condition for Dirac fermions to exist. The semiconductivity of HOT graphene is dependent on the localized π bonding. A corresponding series of nanotubes is rolled up from the HOT graphene sheet and shows distinctive electronic structures depending on the topology. The set of (0,1) n ( нет ≥ 3) HOT graphene nanotubes reveals a character of semimetallicity and Dirac cones that are composed by π states. A non-negligible k F shifting along the allowed k line arises under the curvature effect when the tube radius gets smaller (3 ≤ n ≤ 5). However, the ultra-small nanotube (0,1)2 begins to deviate from the π state-based k F shifting effect showing a transformation to metallicity. Finally, an σ-π hybridization takes the place of the π states at Fermi level in nanotube (0,1)1, where a low-lying σ* band intersection appears at the Fermi level and forms a semimetallicity again. Another set of tubes (1,0) n shows various band gaps (0~ 0.51 eV), which is continuously adjustable with the tube size. The band gaps of (1,0) n ( нет ≥ 3) nanotubes turn out to be determined by a competition mechanism between the k line moving and the k F shifting effect. The zone-folding approximation indicates a k line moving and results in the zigzag and periodical band gap changing curve in big tubes (n ≥ 8), while the k F shifting effect gets stronger and causes a dramatic decrease of band gaps in small tubes (7 ≥ n ≥ 3). Zero-gap semimetallic tubes appear periodically under the competition.
Доступность данных и материалов
Authors declare that the datasets used and/or analyzed during the current study are available to the readers and included in this article.
Сокращения
- 1D:
-
One-dimensional
- 2D:
-
Двумерный
- 3D:
-
Трехмерный
- BZ:
-
Brillouin zone
- CBM:
-
Минимальная зона проводимости
- DFT:
-
Функциональная теория плотности
- DOS:
-
Плотность состояний
- GGA:
-
Generalized-Gradient Approximation
- HOT :
-
Hexagons, octagons, and tetragons
- PBE:
-
Perdew–Burke–Ernzerh
- VASP:
-
Пакет имитационного моделирования Vienna Ab initio
- VBM:
-
Максимальный диапазон валентности
Наноматериалы
- Управление памятью C++:создание и удаление
- НОВАЯ МОДЕЛЬ B + МАЛИНЫ PI 3 ФУНКЦИИ И ПОКУПКА
- Графен в динамиках и наушниках
- Добавки:графеновые нанотрубки во фторэластомерах приносят пользу нефтегазовому и автомобильному секторам
- Нейлон / модифицированная смола СИЗ для требовательных автомобильных применений в жарких и влажных условиях
- Новые роботы:экономичные и первоклассные
- Новости! Новый завод и офис
- Новый клей CARC более эффективен и экономичен
- BS 4360, класс 43A, горячекатаный
- Процесс горячей и холодной прокатки



