Развитое выражение химического потенциала для быстрой деформации электродов из наночастиц литий-ионных батарей

Введение

Для разработки портативных электронных устройств, электромобилей и крупномасштабных накопителей энергии в литиевых батареях предлагается использовать ряд материалов электродов высокой емкости, таких как кремний, которые сильно изменяются в объеме во время литирования [1,2 , 3]. Напряжение, вызванное однородной объемной деформацией, называется напряжением, вызванным диффузией, которое может вызвать хрупкое разрушение во время циклической зарядки и разрядки, и этот отрицательный эффект дополнительно снижает емкость аккумулятора [4]. Композитные материалы электродов литий-ионной батареи обычно сложны, а их морфология различна, что затрудняет объяснение поведения батареи теорией или уравнением. В теоретических моделях свойства композиционных материалов обычно моделируются с учетом изменения параметров материала электродов в пространственных координатах, а межфазный эффект композиционных материалов не учитывается. В настоящее время в теоретической модели в основном рассматриваются три типичных формы электродов:сферическая, цилиндрическая и пластинчатая. Среди них сферические и цилиндрические формы обычно являются одномерными моделями, и доступны как одномерные, так и двухмерные модели для пластинчатых электродов. В последнее время ряд исследований был сосредоточен на индуцированном диффузией напряжении в электродах из кремниевых наночастиц литий-ионных аккумуляторов. Например, Yang et al. [5] представили хемо-механическую модель для исследования индуцированного литированием фазового превращения, морфологической эволюции, образования напряжений и разрушения нанопроволок кристаллического кремния. Ли и др. [6] исследовали влияние локальной скорости на вызванное диффузией напряжение в электродах из кремниевых наночастиц. Zhao et al. [7] проанализировали вызванное диффузией напряжение с учетом неупругой деформации основного материала. Во всех этих вышеупомянутых работах фундаментальная физика связана с диффузией атомов или ионов в твердых телах под действием нескольких движущих сил. Атомная диффузия в твердом теле может изменить твердый состав по сравнению с его стехиометрическим состоянием и зависеть от напряжения, вызванного диффузией. Такое взаимодействие напряжения и диффузии регулируется термодинамическим равновесием твердых тел.

Ларче и Кан [8] разработали термодинамическую основу для многокомпонентных твердых тел, которые достигают равновесия при негидростатическом напряжении. Каркас был основан на предположении, что деформация, вызванная изменением состава, мала и изотропна. В результате был введен химический потенциал, зависящий от напряжения, для учета взаимодействия между напряжением и диффузией. Ву [9] вывел другой химический потенциал, зависящий от напряжения, в котором участвует тензор импульса Эшелби вместо гидростатического напряжения Коши. Исходя из этого, Cui et al. [10] предложили новый химический потенциал для конечной деформации твердых тел. Однако в этих работах вывод должен быть строгим только тогда, когда деформация мала или скорость деформации достаточно мала по сравнению с диффузией. Для кремниевого электрода, вероятно, будет существенная ошибка из-за его большого объемного расширения состава (∼ 400%) при быстром литиировании.

В этой статье мы представляем развитое выражение химического потенциала без предположения о низкой скорости деформации, отличное от традиционного выражения Cui [10]. Эта модель создана для быстрой деформации электродов во время зарядки или разрядки и не зависит от морфологии, потому что химический потенциал является интенсивной величиной, а не экстенсивной величиной. Разница между этими двумя выражениями химического потенциала в распределении напряжения и концентрации Li анализируется как при потенциостатических, так и при гальваностатических операциях в электродах из наночастиц Si. Результат показывает, что разница увеличивается с увеличением скорости деформации. Критический радиус, при котором нет разницы между потоком лития, вызванным этими двумя выражениями химического потенциала, а также гидростатическим напряжением Коши в течение большей части литиированного процесса, определяется одновременно.

Методы

Механические уравнения

Введение лития в электроды может вызвать изменение объема. Для удобства мы используем два способа описания деформации и движения твердых тел:лагранжево и эйлерово описание. Движение материальных частиц в сплошной среде можно описать

где x - координаты Эйлера, X - координаты Лагранжа, а U - поле смещения. Изменение формы сплошного твердого тела можно охарактеризовать тензором градиента деформации, задаваемым

где Grad представляет оператор градиента в лагранжевом описании, а I - единичный тензор второго порядка.

Для сферической частицы координаты Лагранжа и координаты Эйлера материальной точки равны (R, Θ, Φ) и (r, θ, φ) соответственно в сферической системе. Тогда тензор градиента деформации F находится как

Во время зарядки или разрядки изменение формы электрода можно разделить на два процесса:(а) изменение формы из-за вставки лития и (б) обратимая упругая деформация. Эти два процесса деформации можно описать двумя отдельными тензорами градиентов, а тензор градиентов полной деформации можно записать как

где F ^e представляет собой упругую деформацию, F ^c представляет собой изменение формы из-за вставки лития. Уравнение (4) представляет собой процесс перехода материала электродов из исходного (недеформированного) состояния в текущее (деформированное) состояние. Предполагая, что изменение формы из-за вставки лития является изотропным, F ^c может быть выдан

где Ω представляет собой парциальный молярный объем.

Из уравнения. (3–5) тензор градиента упругой деформации F ^e есть

Суммарный тензор деформаций Грина-Лагранжа E можно записать как

где тензор упругих деформаций E ^e и тензор деформации, вызванной диффузией E ^c являются

соответственно.

Подставляя уравнение. (6) в уравнение. Согласно формуле (8) радиальная и тангенциальная компоненты тензора деформаций Грина-Лагранжа равны

Определяющее соотношение для деформации может быть определено из плотности энергии деформации как

где W - плотность энергии упругой деформации в лагранжевом описании, а P - первое напряжение Пиолы-Кирхгофа. Кроме того, если материал линейно эластичный, W можно записать как квадратичную функцию тензора деформаций Грина-Лагранжа

Здесь E _h и ν - модуль Юнга и коэффициент Пуассона, соответственно, C - тензор жесткости, а det ( F ^c ) является определителем тензора градиента деформации для деформации, вызванной диффузией.

Наконец, первое напряжение Пиолы-Кирхгофа определяется как

Комбинируя уравнения. (5), (9), (10) и (13) соответствующие компоненты первого тензора напряжений Пиолы-Кирхгофа (P-K) равны

И первое напряжение P-K должно удовлетворять условию равновесия при отсутствии массовой силы

с начальными и граничными условиями

Уравнение массового транспорта

Концентрация и диффузионный поток лития в электродах, которые являются функциями координат и времени, будут называться C . ( X , T) и J ( X , T) в лагранжевом описании, и им должно удовлетворять уравнение массопереноса, записанное как

где Div представляет оператор дивергенции в лагранжевом описании. Учитывая характеристику сферической симметрии, диффузия происходит только в радиальном направлении, и мы используем J ( R , t) для представления радиальной составляющей J ( X , т). В сферической системе уравнение. (18) становится

Диффузия лития в электродах обусловлена ​​градиентом химического потенциала, а радиальный поток Дж ( R , t) пропорционален градиенту химического потенциала μ , как [11]

где D коэффициент диффузии, R _г - газовая постоянная, а T это температура. μ определяется как отклонение полной плотности энергии от концентрации и может быть записано как

Предположим, что плотность энергии системы Π может быть описана как сумма плотности химической энергии и плотности энергии деформации. Итак, полную плотность внутренней энергии можно записать как

Подставляя уравнение. (22) в уравнение (21) химический потенциал μ может быть показано

где μ ₀ ( C ) и τ ( E ^e , C ) являются независимой от напряжения и зависимой от напряжения частью химического потенциала соответственно. И

где μ ₀ - константа, представляющая химический потенциал в стандартном состоянии, а γ - коэффициент активности, который представляет эффекты взаимодействия между атомами / молекулами. Для разбавленного раствора взаимодействия между атомами / молекулами незначительны; таким образом, γ =1.

Мы фокусируемся на напряженно-зависимой части химического потенциала τ ( E ^e , C), которая является производной от плотности энергии деформации W относительно концентрации лития C. Традиционно Π ( X , T) считается плотностью свободной энергии Гельмгольца, и поэтому этот шаг выполняется для фиксированной деформации, записанной как [11]

Нижний индекс H означает, что это вызвано плотностью свободной энергии Гельмгольца. Химический потенциал оказывается

где σ _м является гидростатическим напряжением Коши в описании Эйлера и может быть получено

Стоит отметить, что жесткость C материала электрода не зависит от концентрации лития C в формуле. (12). Кроме того, det ( F ^e ) ≈ 1 является широко принятым, поэтому обычно его игнорируют. В остальной части этой статьи мы называем уравнение. (26) как традиционное выражение химического потенциала. С другой стороны, Π ( X , T) считается плотностью свободной энергии Гиббса в некоторых исследованиях [12, 13] по модели фазового поля, так что мы не можем получить развитое выражение для τ ( E ^e , C) и

Нижний индекс G означает, что это вызвано плотностью свободной энергии Гиббса. В этом случае μ становится

и мы называем уравнение. (29) как развитое выражение химического потенциала.

Уравнение массопереноса состоит из уравнений. (19), (20), (26) и (29) с традиционными и развитыми выражениями химического потенциала. В оставшейся части статьи мы сравним влияние этих двух выражений химического потенциала на напряжение, вызванное диффузией, и концентрацию лития при различных методах зарядки.

В термодинамике свободная энергия Гельмгольца - это термодинамический потенциал, который измеряет полезную работу, получаемую от замкнутой термодинамической системы при постоянной температуре и объеме. Напротив, свободная энергия Гиббса измеряет максимум обратимой работы, которая может быть выполнена термодинамической системой при постоянной температуре и давлении. В твердых телах с низким уровнем напряжения свободная энергия Гиббса приблизительно эквивалентна свободной энергии Гельмгольца, поскольку деформация твердых тел обычно мала. Это предположение подходит для большинства твердых материалов из-за их небольшой деформации, вызванной диффузией, но за исключением кремния из-за его большого объемного расширения во время литирования. Фактически, диффузия и деформация происходят одновременно, поэтому нецелесообразно предполагать, что деформации не происходит при изменении концентрации. Даже в этом случае, как видно из уравнения. Согласно (25) традиционное выражение химического потенциала остается точным при достаточно низкой скорости деформации. Однако при быстром литиировании электрода из наночастиц Si это может привести к большим ошибкам.

Электрод литиирован с постоянной концентрацией литий-иона на его поверхности, а именно в потенциостатическом режиме, или с постоянным потоком на его поверхности, а именно в гальваностатическом режиме. Граничные условия уравнения. (19) являются

соответственно. Начальное условие записывается как

за каждую операцию зарядки. Здесь C _макс - максимальная концентрация лития в материале и j ₀ - константа, представляющая ток заряда.

Числовая реализация

Получить аналитическое решение вышеупомянутой системы, состоящей из уравнений в частных производных, очень сложно, если вообще возможно. С уравнениями. (1) - (3) и (13) - (18) мы рассчитываем эволюцию вызванного диффузией напряжения и концентрации лития численно с помощью программного обеспечения COMSOL multiphysics. Изучено литирование кремниевого наноэлектрода как при потенциостатических, так и при гальваностатических операциях с различными выражениями химического потенциала. Свойства материала Si и рабочие параметры, использованные при моделировании, перечислены в таблице 1. Для удобства на рисунках используется соответствующая безразмерная замена координаты, напряжения и концентрации.

Чтобы исследовать разницу между различными выражениями химического потенциала в разное время в сферическом Si-электроде, состояние заряда (SOC) рассчитывается как

Диффузионные потоки, вызванные напряжением, в лагранжевом описании описываются как

представляющий поток, вызванный различными выражениями химического потенциала, соответственно.

Результаты и обсуждение

На рис. 1 показано пространственное распределение концентрации лития, радиального напряжения и кольцевого напряжения в сферическом Si-электроде при гальваностатическом режиме на нескольких SOC. Для сравнения включены численные результаты как с разработанными, так и с традиционными выражениями химического потенциала, которые представлены сплошными линиями и символами треугольников, соответственно. Для каждого SOC на рис. 1а сплошная линия почти перекрывает символы треугольника. Влияние различных выражений химического потенциала на концентрацию лития можно не учитывать. На рис. 1b и рис. 1c для SOC 46,7% и 65,5% сплошные линии выше треугольников в центре, в то время как они почти перекрываются снаружи, как и в других SOC. В целом наблюдается небольшое влияние на концентрацию лития и напряжения при гальваностатическом режиме. На рис. 2 показаны пространственные распределения концентрации лития, радиального напряжения и кольцевого напряжения в сферическом Si-электроде при потенциостатической работе на нескольких SOC. Следует отметить, что радиальное и кольцевое напряжения сначала увеличиваются, а затем уменьшаются с увеличением SOC как на рис. 1, так и на рис. 2. Это связано с тем, что кремниевый электрод в исходном состоянии или полностью литированном состоянии не имеет напряжений, поскольку нет градиента концентрации. По сравнению с рис. 1а разница между сплошными линиями и треугольниками на рис. 2а больше. Из-за того, что концентрация лития на поверхности является постоянной C _макс в потенциостатическом режиме скорость заряда выше, чем скорость деформации в гальваностатическом режиме, а также скорость деформации. Однако общая деформация при одном и том же SOC практически одинакова независимо от метода заряда, просто требуется разное время. Это указывает на то, что влияние на распределение лития, вызванное различными выражениями химического потенциала, связано только со скоростью деформации, а не с деформацией, и увеличивается с увеличением скорости деформации. Фактически, существующие эксперименты показывают, что кремниевые электроды очень быстро деформируются во время литирования при определенных режимах зарядки. Как видно из рис. 3 [17], Si-анод полностью деформируется за 1 мин с потенциалом 2 В по отношению к металлическому Li. В этом случае результаты, полученные с помощью этих двух выражений химического потенциала, будут значительно отличаться. К сожалению, в этом случае нельзя точно измерить напряжение электрода и, следовательно, его нельзя количественно сравнить с нашей моделью.

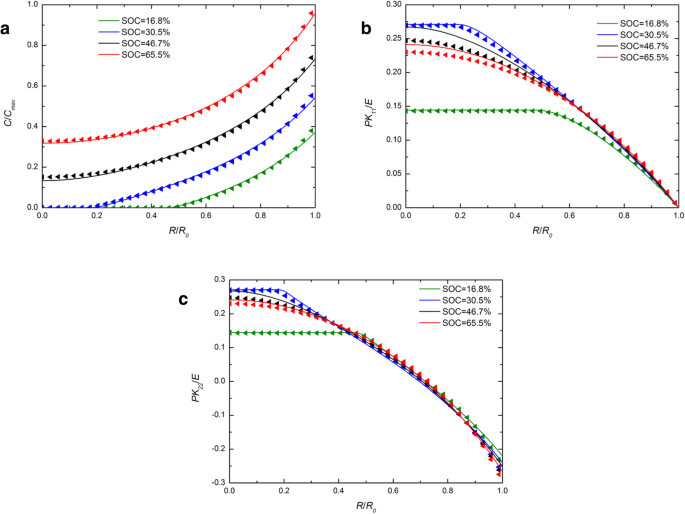
Пространственное распределение ( a ) концентрация лития, ( b ) радиальное напряжение и ( c ) кольцевое напряжение в сферическом Si-электроде при различных SOC в гальваностатическом режиме (сплошные линии представляют результаты с традиционным выражением химического потенциала; треугольные линии представляют результаты с развитым выражением химического потенциала)

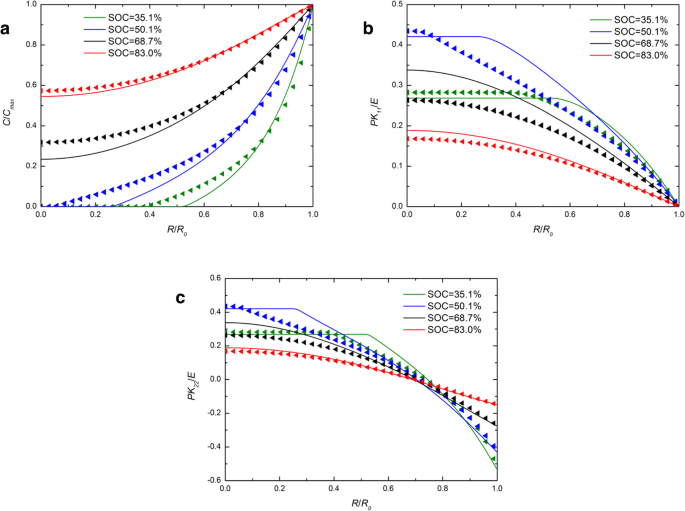
Пространственное распределение ( a ) концентрация лития, ( b ) радиальное напряжение и ( c ) кольцевое напряжение в сферическом электроде из наночастиц Si при различных SOC при потенциостатической работе (сплошные линии представляют результаты с традиционным выражением химического потенциала; треугольные линии представляют результаты с развитым выражением химического потенциала)

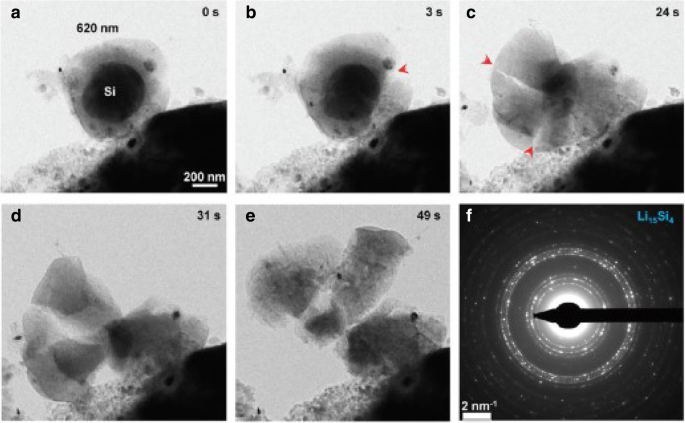
Быстрая деформация отдельно стоящего SiНЧ с длиной волны 620 нм в процессе химического литирования за 1 мин. а - е Временная последовательность зарождения и роста трещины. е EDP, указывающий на образование поликристаллического Li ₁₅ Si ₄ как полностью литированная фаза

На рисунке 4 показано пространственное распределение J _H / Дж _G в сферическом Si-электроде на разных SOC в гальваностатическом режиме с разными j . На рис. 4 сплошные линии почти совпадают с треугольниками, что указывает на то, что различные выражения химического потенциала незначительно влияют на отношение J _H и Дж _G . Очевидно, что диапазон значений J _H / Дж _G увеличивается с увеличением тока заряда. Это связано с тем, что больший ток заряда приводит к более высоким скоростям деформации и, следовательно, вызывает большее влияние различных выражений химического потенциала. Отношение всегда больше 1 в центре и меньше 1 на поверхности. Это предполагает, что поток, полученный из развитого выражения химического потенциала на поверхности, больше, чем полученный из традиционного выражения, в то время как противоположное верно в центре. Мы замечаем, что все сплошные линии и треугольники на рис. 4 практически пересекаются с одной точкой. Кроме того, отношение, соответствующее пересечению, всегда равно 1, независимо от того, каким током заряжается электрод. Это предполагает, что существует критический радиус, в котором поток меньше зависит от различных выражений химического потенциала. Мы называем это областью, независимой от химического потенциала (CIR). Очевидно, что CIR всегда находится рядом с поверхностью сферического электрода и ближе к поверхности по мере увеличения тока заряда.

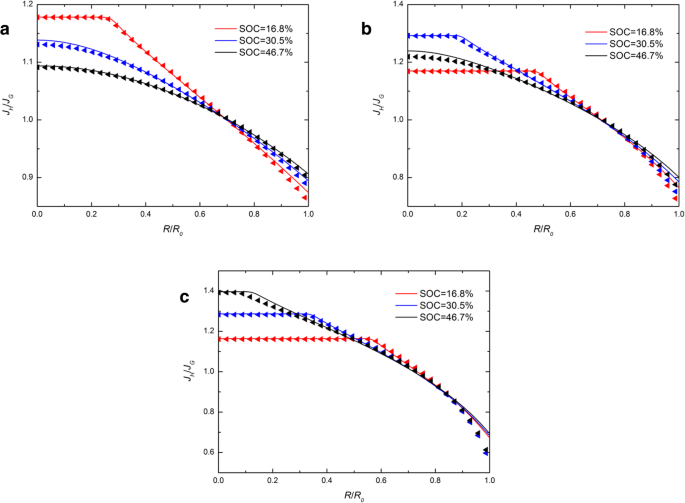
Пространственное распределение J _H / Дж _G в электроде из сферических наночастиц Si на различных SOC в гальваностатическом режиме с ( a ) j =0,5 j ₀ , ( b ) j = j ₀ , и ( c ) j =1,5 j ₀ (сплошные линии представляют результаты с традиционным выражением химического потенциала; треугольные линии представляют результаты с развитым выражением химического потенциала)

Сравнивая традиционные и развитые химические потенциалы в формуле. (26) и уравнение. (29) установлено, что гидростатическое напряжение Коши σ _m это ключ к различию между этими двумя выражениями. Чтобы исследовать причины CIR, пространственное распределение σ _m / E в сферическом Si-электроде при различных SOC в гальваностатическом режиме с разными выражениями химического потенциала приведены на рис. 5 и 6. Очевидно, что почти все кривые пересекаются в одной точке на CIR и гидростатическом напряжении Коши σ _м близко к 0 в этой точке, за исключением начала зарядки (SOC =6,2%). Это означает, что σ _m в CIR поддерживается на низком уровне (почти 0) в течение большей части периода зарядки. Можно интерпретировать, что два выражения химического потенциала почти эквивалентны, когда гидростатическое напряжение σ _m близко к 0. Это может частично объяснить, почему появляется CIR, но этого недостаточно, чтобы объяснить особенности кривых на σ _m . Ее необходимо решить в ходе нашего следующего исследования.

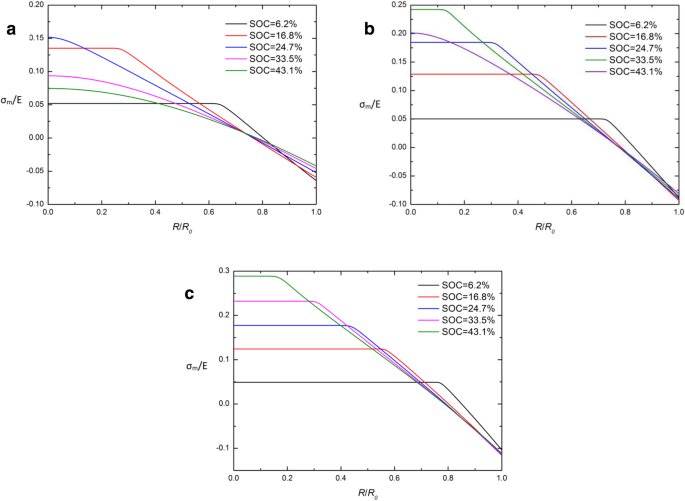
Пространственное распределение σ _м / E в электроде из сферических наночастиц Si на различных SOC в гальваностатическом режиме с традиционным выражением химического потенциала и ( a ) j =0,5 j ₀ , ( b ) j = j _0, и ( c ) j =1,5 j ₀

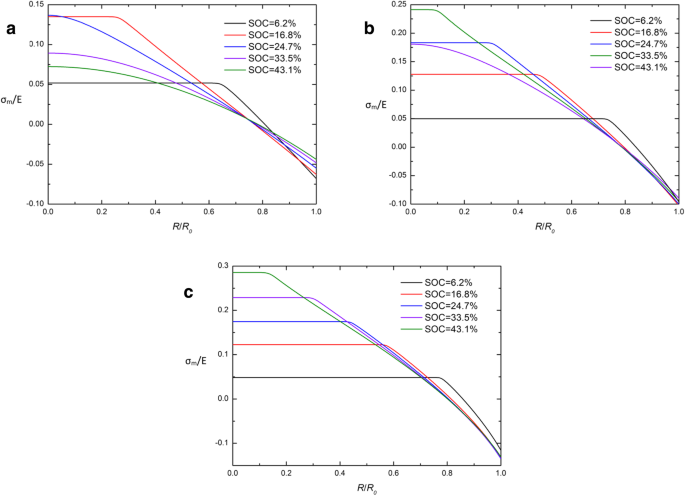
Пространственное распределение σ _м / E в электроде из сферических наночастиц Si на различных SOC в гальваностатическом режиме с развитым выражением химического потенциала ( a ) j =0,5 j ₀ , ( b ) j = j ₀ , и ( c ) j =1,5 j ₀ с

Выводы

В этой работе предлагается развитое выражение химического потенциала без предположения о низкой скорости деформации, в отличие от развитого выражения, которое широко используется в настоящее время. Разница между традиционным и развитым выражениями химического потенциала в распределении напряжения и концентрации в электродах из наночастиц Si обсуждается как при потенциостатических, так и при гальваностатических операциях.

Результат показывает, что эффектом, вызванным различными выражениями химического потенциала, можно пренебречь при гальваностатическом режиме, но он значительный при потенциостатическом режиме. Установлено, что эффект связан скорее со скоростью деформации, чем с деформацией, и может быть больше с увеличением скорости деформации. Принимая во внимание допущение о низкой скорости деформации в традиционном выражении химического потенциала, считается, что результаты, полученные с помощью развитого выражения химического потенциала, являются более надежными. Область, не зависящая от химического потенциала (CIR), где поток, вызванный традиционным и развитым химическим потенциалом, почти одинаков в течение большей части процесса лития, находится вблизи поверхности электрода наночастиц. Кроме того, CIR становится ближе к поверхности с увеличением тока заряда. Аналогичное явление также проявляется на кривых гидростатических напряжений Коши. Гидростатическое напряжение Коши σ _м сохраняет постоянство и поддерживается на низком уровне (почти 0) в CIR большую часть времени, независимо от того, какое выражение химического потенциала используется. О таких результатах еще не сообщалось в литературе.

Доступность данных и материалов

Наборы данных, проанализированные в ходе текущего исследования, доступны у соответствующего автора по разумному запросу.

Сокращения

CIR:

Область, где диффузионный поток, вызванный этими двумя выражениями химического потенциала, почти одинаков